基于变分模态分解的水泵水轮机暂态过程流激振动信号分析1)
郑祥豪 张宇宁, 张 梁 李金伟
*(华北电力大学电站能量传递转化与系统教育部重点实验室,北京 102206)
†(雅砻江流域水电开发有限公司,成都 610056)
**(中国水利水电科学研究院,北京 100048)
随着我国抽水蓄能行业的快速发展,越来越多高参数的水泵水轮机投入使用[1-2]。不同于其他类型的水轮机,水泵水轮机的运行水头和转速均较高,并且在设计过程中需要兼顾抽水和发电两种工况下的性能,因此水泵水轮机的动静干涉作用十分显著。这种类型的动静干涉作用是指,在转轮旋转过程中,当流体流经旋转叶轮与静止的活动导叶之间的无叶区时,由转轮叶片引起的旋转流跟活动导叶尾端引起的水流扰动之间的相互作用所引发的异常压力脉动及其传播过程中所激发的振动现象。由于大部分水泵水轮机需要承担电网调峰以及配合新能源并网的任务,因此需要频繁地经历启动和停机等一系列暂态过程[3]。在这些暂态过程中,机组受到由流体动力激发的振动显著增强,这对于机组的安全稳定运行来说是一大考验。水泵水轮机发电工况停机暂态过程是指停机指令发出后,机组从电网解列,随后导叶快速关闭以及转速逐渐减小的过程。在该暂态过程中,从机组采集到的振动信号属于非稳态振动信号,通过振动信号的时频分析能够得到机组在经历不同转速区时的振动幅度和流激频率信息。机组能否按照计划正常停机,是影响整个电站运行安全的直接因素,因此研究水泵水轮机发电工况停机暂态过程的振动信号具有非常重要的工程意义。
由于在水泵水轮机发电工况停机暂态过程中所采集到的振动信号具有较强的时变特征,传统的快速傅里叶变换已经不能满足分析要求。目前用于信号时频分析的方法主要包括短时傅里叶变换、小波变换、希尔伯特−黄变换等[4]。其中,作为希尔伯特−黄变换的核心思想,经验模态分解能够实现对信号的自适应分解以及拥有较高的时频分辨率,被认为是非稳态信号分析领域的重要突破[5]。目前已有较多文献使用经验模态分解对水电机组领域的工程信号进行了研究。张飞等[6]使用经验模态分解分析了水电机组甩负荷暂态过程中上导轴心的运动轨迹。薛延刚等[7]使用经验模态分解和希尔伯特时频谱图识别出了水电机组空化信号的主要频率成分。然而,由于在水泵水轮机发电工况停机暂态过程中,导叶开度与机组转速变化范围较大,信号中的流激频率时变特征较强,若使用经验模态分解对其进行分析,会出现模态混叠与产生虚假分量等问题。因此迫切需要使用更为先进的信号分析方法,以更加精确地提取信号中的时频特征。
针对上述经验模态分解中存在的问题,Dragomiretskiy 等[8]提出了变分模态分解。相比经验模态分解,变分模态分解能够更为有效地提取信号中的不同频率成分,且分解出来的模态函数分量具有较强的物理意义。于晓东等[9]使用变分模态分解以及排列熵对水电机组振动信号进行了降噪研究,取得了良好的效果。付文龙等[10]使用奇异值分解结合变分模态分解的方法对水电机组摆度信号进行了降噪研究,发现其降噪效果要优于经验模态分解。
本文使用变分模态分解对水泵水轮机发电工况停机暂态过程顶盖振动信号进行了分解,得到了若干个本征模态函数分量IMF(intrinsic mode function),并使用希尔伯特时频变换对上述模态函数分量进行时频分析,最后获得了高分辨率的信号时频图。该方法有效地改善了经验模态分解中存在的模态混叠现象,能够更为明显地观察到暂态过程振动信号中主要由流体动力激发的频率成分和相对应的时间信息,非常适用于水泵水轮机发电工况停机暂态过程非稳态振动信号的时频分析。
1 基本原理介绍
1.1 经验模态分解算法
经验模态分解算法的主要步骤如下[5]:首先,使用三次样条函数对信号中包含的所有极大、极小值点分别进行插值拟合,得到信号的上、下包络线,并计算二者的均值曲线。其次,计算原始信号与均值曲线的差值,由于第一次计算的差值通常不是一个标准的模态函数分量IMF,因此需要重复多次计算该差值,直到差值满足筛分停止的条件,此时得到的第一个模态函数分量简称为IMF1。之后,对剩余的信号再次按照上述步骤进行处理,直至得到全部的模态函数分量IMF和最终的信号残差成分。
1.2 变分模态分解算法
变分模态分解算法的主要步骤如下[8]:首先,将各个模态函数分量定义为调频、调幅信号,且各个模态函数分量的频带是有限并且是相互分离的。其次,借助希尔伯特变换、信号频移特性、高斯平滑解调信号的方法构造变分约束问题,以求得各个模态函数分量的频带宽度。之后,引入二次惩罚因子和拉格朗日乘子,并使用乘法算子交替方向法和帕塞瓦尔傅里叶等距变换得到各个模态函数分量的频带宽度、中心频率和拉格朗日乘子的更新信息。最后,当求解过程满足求解精度时,停止迭代运算并输出若干个模态函数分量,并使用傅里叶逆变换将各个模态函数分量IMF从频域转化为时域。
关于变分模态分解算法中的参数设置,本文选取预分解的模态函数分量的数量为7,二次惩罚因子为2000,判别精度为10−7,噪声容忍度为0。
1.3 希尔伯特时频分析原理
希尔伯特时频分析的主要步骤如下[5]。首先,对信号分解后的各个模态函数分量进行希尔伯特变换,并构造各个模态函数分量的解析信号。其次,对各个解析信号的相位进行时间求导进而得到各个模态函数分量的瞬时频率信息。之后,将上述结果表示在时间−频率的二维平面上,得到了各个模态函数分量的希尔伯特幅值谱。最后,将分解的所有模态函数分量的希尔伯特幅值谱展示在同一个时频谱图里,便得到了整个完整信号的希尔伯特时频谱图。
2 实验概况与无量纲参数
2.1 水泵水轮机基本参数
本次实验基于国内某水泵水轮机开展,该机组的基本参数如表1 所示。

表1 本文所使用的国内某水泵水轮机基本参数Table 1 The essential parameters of the pump turbine in China adopted in the present paper
2.2 本文所使用的无量纲参数
为了便于后续分析,本文中将转速n和运行负荷P进行无量纲化。“*” 代表无量纲后的符号,n*表示将机组实际转速n与机组额定转速nrated进行无量纲后的结果,P*表示将机组实际运行负荷P与额定输出功率Prated进行无量纲后的结果。
2.3 实验工况说明
顶盖测点位于机组正上方,靠近流道,其振动容易受到机组内部复杂流动的影响,属于水泵水轮机典型的振动测点之一。本次实验过程概况如下,机组先是稳定运行在无量纲负荷P*= 52% 左右。随后停机指令发出,机组与电网解列,活动导叶开度与机组有功功率均快速降为0。与此同时,在机组转速逐渐下降的过程中,使用低频速度输出振动传感器采集了顶盖X方向的振动信号,信号的采样频率为1000 Hz。为了便于后续分析,本文截取完整振动信号中的一段(时长16 s) 进行研究,该段信号对应的实测机组无量纲转速变化如图1 所示,机组无量纲转速n*大约从54.7% 下降到49.9%。

图1 水泵水轮机发电工况停机暂态过程无量纲转速n*变化曲线Fig.1 The variation curve of the dimensionless rotational speed (n*) of the pump turbine during the transient process of shutdown from the generating mode
3 水泵水轮机流激振动信号时频分析
3.1 信号时域图与快速傅里叶变换频谱图
图2为国内某水泵水轮机发电工况停机暂态过程顶盖X方向的振动信号时域图以及快速傅里叶变换(fast Fourier transform, FFT) 频谱图,振动信号时域图能够反映出振动幅值随时间的变化情况,FFT 频谱图能够反映出振动信号中所包含的所有频率成分和相对应的幅值信息。可以观察到,在停机过程中,振动时域信号的峰峰值不断减小。当时间t= 0~1 s 范围内时,97% 置信区间内信号的混频双峰峰值为2.18 mm/s,而当时间t= 15~16 s范围内时,97% 置信区间内信号的混频双峰峰值为0.68 mm/s,表明整体的振动幅值逐渐减小。另外,FFT 频谱图中信号主频约为f=69.06 Hz,幅值约为0.10 mm/s,但由于FFT 只能从频域的角度分析信号,无法显示出各个频率相对应的时间信息,因此该频率的来源还需进一步采用经验模态分解、变分模态分解和希尔伯特时频图等方法来确定。
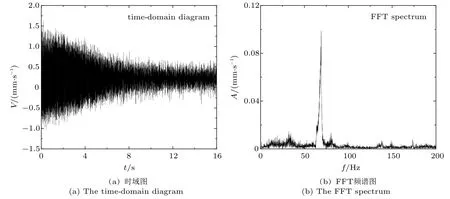
图2 水泵水轮机发电工况停机暂态过程顶盖X 方向振动信号Fig.2 The vibrational signal in the X direction of top cover of the pump turbine during the transient process of shutdown from the generating mode
3.2 经验模态分解分析结果
对水泵水轮机停机暂态过程顶盖X方向振动信号进行经验模态分解分析,结果如图3 所示,一共分解得到了10 个模态函数分量IMF1~IMF10和1 个信号残差成分。图3(a) 为经验模态分解分析得到的10 个模态函数分量和1 个信号残差成分的时域波形图,图3(b) 表示10 个模态函数分量和1 个信号残差成分的FFT 频谱图。
从图3 可以观察到,经验模态分解分析结果中的第一个模态函数分量IMF1与第二个模态函数分量IMF2中同时出现了约为f=69.06 Hz 的主频成分。并且,第二个模态函数分量IMF2中同时存在约为f=69.06 Hz 的主频成分和其他小于f=69.06 Hz 的随机频率成分。上述两种现象均属于经验模态分解的模态混叠问题,因此该主频成分(约为f=69.06 Hz)不能被有效单独提取。
3.3 变分模态分解分析结果
对水泵水轮机发电工况停机暂态过程顶盖X方向振动信号进行变分模态分解分析,结果如图4 所示,一共分解得到了7 个模态函数分量IMF1~IMF7。类似地,图4(a) 为变分模态分解分析得到的7 个模态函数分量的时域波形图,图4(b) 表示7个模态函数分量的FFT 频谱图。
从图4 可以观察到,变分模态分解分析结果中约为f= 69.06 Hz 的主频成分被有效地分解到了第二个模态函数分量IMF2中,有效避免了经验模态分解中存在的模态混叠问题,提高了信号分解时的精度,减少了其他无用频率对主频的干扰,对识别机组的运行状态起到了非常重要的作用。
3.4 基于经验模态分解和变分模态分解的希尔伯特时频分析结果对比
在图3 的经验模态分解分析结果和图4 的变分模态分解分析结果中,只是确定了分解得到的各个模态函数分量IMF中的频率成分,暂时还无法观察到每种频率所对应的时间信息。下面使用希尔伯特时频变换对各个IMF进行分析,并将所有IMF的时频信息集合在同一个希尔伯特时频谱图中,以便于观察整个信号中的时频分布特征。

图3 水泵水轮机发电工况停机暂态过程顶盖X 方向振动信号经验模态分解分析结果Fig.3 The analysis results of empirical mode decomposition of the vibrational signal in the X direction of top cover of the pump turbine during the transient process of shutdown from the generating mode
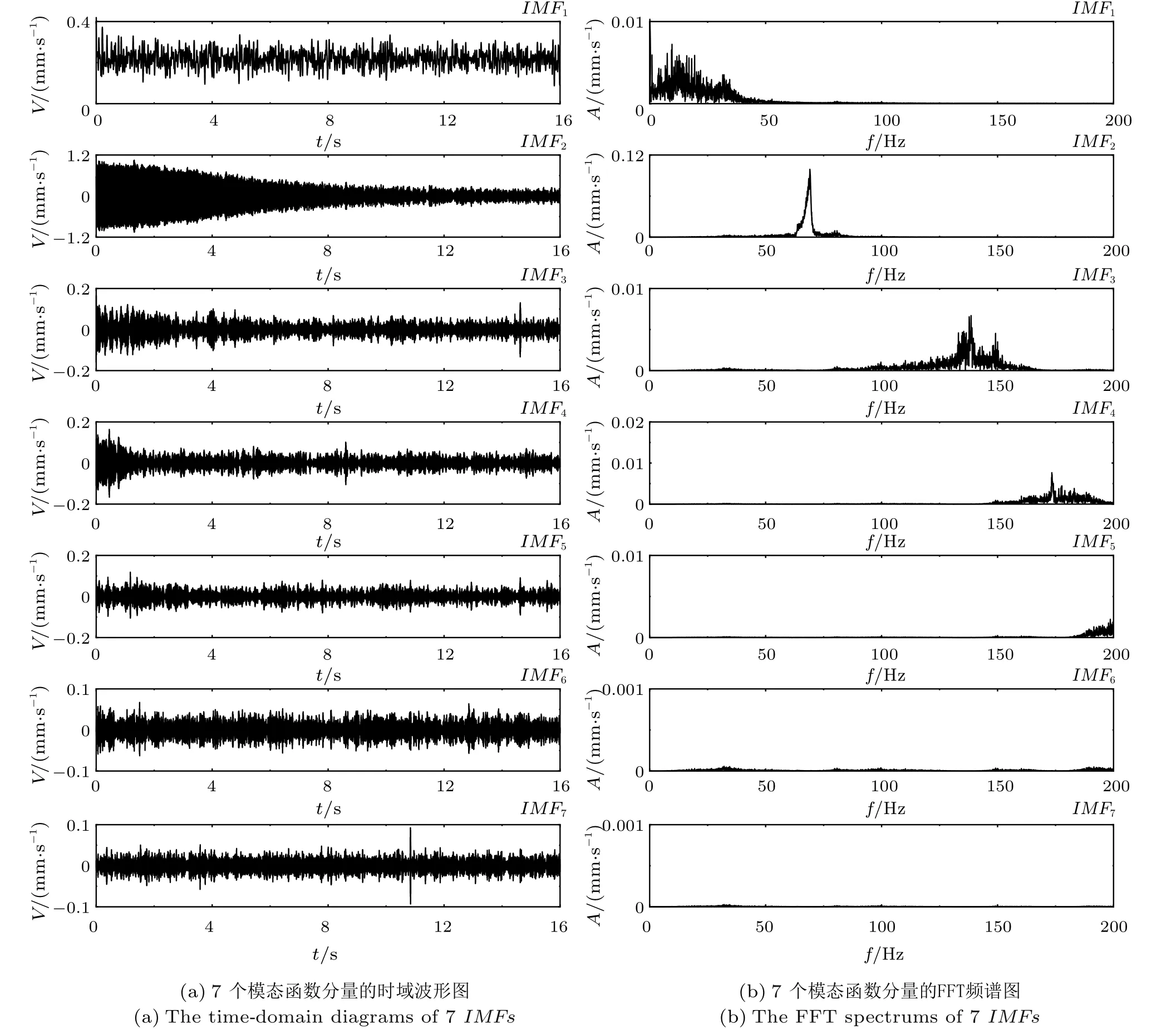
图4 水泵水轮机发电工况停机暂态过程顶盖X 方向振动信号变分模态分解分析结果Fig.4 The analysis results of variational mode decomposition of the vibrational signal in the X direction of top cover of the pump turbine during the transient process of shutdown from the generating mode
图5和图6 分别展示了基于水泵水轮机停机暂态过程顶盖X方向振动信号经验模态分解和变分模态分解分析结果的希尔伯特时频图。可以观察到,由于经验模态分解结果中存在较为明显的模态混叠现象,因此基于经验模态分解的希尔伯特时频图中频率分布混乱。例如,在时间t=0~8 s 时间段内,虽然在f=69.06 Hz 附近(f=40~100 Hz 范围),时频谱图颜色较深,但无法观察到较为清晰的频率变化规律。另外,从右侧用来表示幅值变化的颜色表可以看出,时频图中的最高幅值超过了3 mm/s。结合图2 中的时域波形来看,该结果明显不太符合实际。而基于变分模态分解的希尔伯特时频图中信号主频率变化规律清晰(主频大约由f= 70.33 Hz 降至64.16 Hz),频率能量较为集中。结合该过程转速变化情况(无量纲转速n*大约由54.7%降至49.9%),可以计算并判断出该过程的顶盖振动主频为2 倍的叶片过流频率,表明此时的顶盖振动与旋转叶轮与静止的活动导叶间的流体异常流动密切相关。此外,在基于变分模态分解的希尔伯特时频图的低频段(f <5 Hz) 能够观察到低频成分,表明此时机组内部流态较为紊乱,可能存在不稳定的涡和回流等现象。同时,从右侧用来表示幅值变化的颜色表可以看出,基于变分模态分解的希尔伯特时频图中的最高幅值约为1.1 mm/s,结合图2 中的时域波形来看,该结果较为合理。
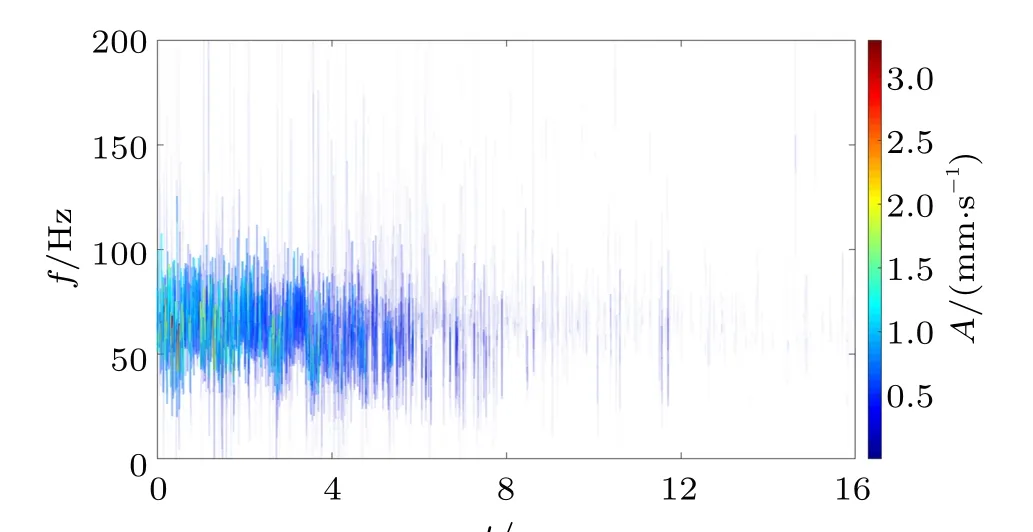
图5 基于水泵水轮机发电工况停机暂态过程顶盖X 方向振动信号经验模态分解分析结果的希尔伯特时频图Fig.5 The Hilbert spectrum based on the analysis results of empirical mode decomposition of the vibrational signal in the X direction of top cover of the pump turbine during the transient process of shutdown from the generating mode
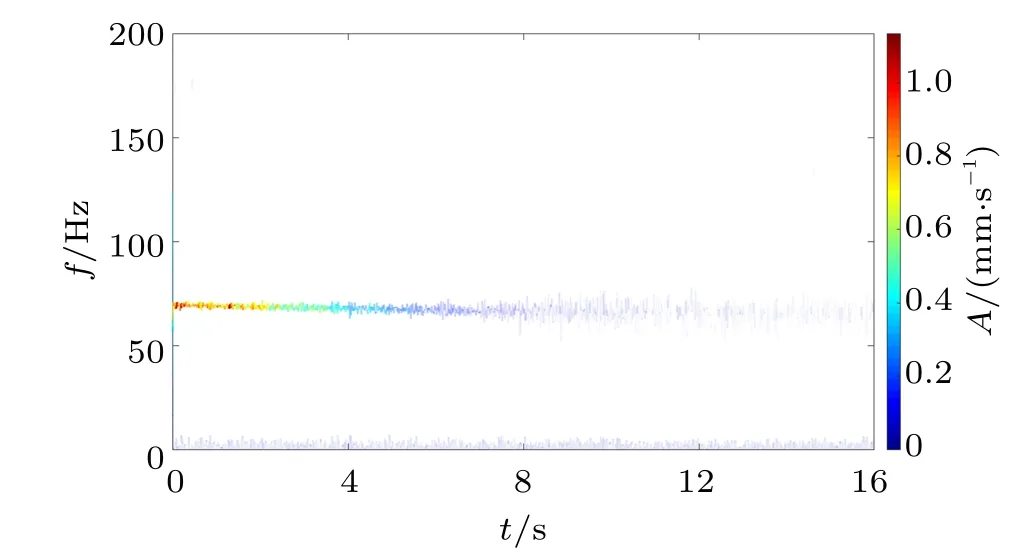
图6 基于水泵水轮机发电工况停机暂态过程顶盖X 方向振动信号变分模态分解分析结果的希尔伯特时频图Fig.6 The Hilbert spectrum based on the analysis results of variational mode decomposition of the vibrational signal in the X direction of top cover of the pump turbine during the transient process of shutdown from the generating mode
为了进一步确定顶盖振动主频(2 倍的叶片过流频率)的来源,这里结合水泵水轮机动静干涉引起的水力激振模式[11-13]的计算公式(k=mB−nG,其中m和n为任意整数,B为转轮叶片数,G为活动导叶数,k为节径)。可以发现当m=2,n=1,k=−2时公式成立,且满足k的绝对值达到最小值2,因此根据节径模式理论可以判断出该主频(m倍的叶片过流频率,此处m=2)为旋转叶轮与静止的活动导叶之间的动静干涉频率。因此,水泵水轮机发电工况停机暂态过程中顶盖X方向振动主要是由于旋转叶轮与静止的活动导叶之间的动静干涉作用而引起的流体异常压力脉动在过流部件中传播所导致的。同时,由于机组停机过程中水流量逐步减小,因此旋转叶轮与静止的活动导叶之间的动静干涉作用也逐渐减弱,时频图中表现为由其引起的同频率振动幅值也逐渐减小。
4 结论
本文基于经验模态分解、变分模态分解以及希尔伯特时频分析法对国内某水泵水轮机发电工况停机暂态过程中的顶盖振动信号进行了研究。本文的主要结论如下。
(1)相比经验模态分解和变分模态分解能够更为精准地提取水泵水轮机发电工况停机暂态过程顶盖振动信号中的主要特征频率成分,有效避免经验模态分解结果中存在的模态混叠现象。
(2)相比经验模态分解,从基于变分模态分解的希尔伯特时频图中能够更为清晰地观察到水泵水轮机发电工况停机暂态过程顶盖振动信号中的时变特征情况,其主频为动静干涉频率,表明在该过程中顶盖振动主要是由于旋转叶轮与静止的活动导叶之间的动静干涉作用而引起的流体异常压力脉动在过流部件中传播所导致的。
(3) 一些复杂的低频流动(比如涡和回流等) 也同样能够引起顶盖的振动,但相比于动静干涉,其贡献较弱。

