高速受电弓气动减阻的仿真优化研究1)

燕永钊 许向红 王烯州 耿浩森 黄思俊

*(中国科学院力学研究所非线性力学国家重点实验室,北京 100190)

†(中国科学院大学工程科学学院,北京 100049)

**(北方工业大学机械与材料工程学院,北京 100144)

††(北京中车赛德铁道电气科技有限公司,北京 100176)

在受电弓设计和制造时,相关研究人员主要考虑其结构安全性与可靠性,对受电弓的优化改进工作,多侧重于提升其弓网耦合性能[1]。然而,随着列车运行速度的提升,受电弓气动减阻成为不容忽视的问题。目前,减阻降噪是高速轨道交通技术发展的重要方向之一,随着运行速度的提升,气动阻力已成为限制列车提速的主要因素之一。已有文献表明,时速300 km/h 时,列车气动阻力占总阻力的90% 以上[2]。目前,对于列车减阻的相关研究工作,多集中于列车头型的改进,对于受电弓的减阻设计研究则相对较少[3-4]。然而,列车高速运行时,受电弓暴露在流线型车体之外,产生较大的气动阻力,是列车气动阻力的主要来源之一[5],约占高速列车气动阻力的12%[6]。减小高速受电弓的气动阻力,对于列车进一步提速,有至关重要的意义。

降低受电弓的气动阻力,主要是通过优化受电弓结构和改变受电弓周围流场两种方式[6-8]。对于优化受电弓结构,光用刚等[7]提出一种滑板前缘为钝头、后缘为近似流线型的设计,这种截面构型具有较好的减阻降噪效果。Li 等[9]通过计算表明改变双滑板型受电弓的滑板间距会影响受电弓的气动阻力。Ito[10]采用滑板与弓角融合式设计,同时在上下臂铰等连结位置包裹减阻罩,避免气流经过交接位置发生复杂流动,降低受电弓的气动阻力。刘海涛等[11]基于仿生原理,提出了带有环状波纹等微结构的杆件减阻设计。此外,减少受电弓的杆件数量,也可降低受电弓的气动阻力[6,12]。对于改变受电弓周围流场,张雷等[13]在受电弓周围增加导流罩,使受电弓来流前方气流偏转,削弱受电弓前的来流强度。孔学舟等[14]提出增加受电弓舱,使受电弓底座沉降进入车体,避免底部直接迎风,从而减小气动阻力。

对比多种受电弓减阻方法,采用仿生杆件设计,工程实现的难度较大；减少受电弓杆件数量,对于弓网受流稳定性的影响需要进一步评估；此外,增加导流罩和受电弓舱虽然降低了受电弓的气动阻力,但是其自身几何尺度较大,本身也会产生较大的气动力,在车体自身原有气动阻力基础上额外增加了气动阻力,对整车减阻而言,其外形方案需要大量的设计论证。如何在不影响原有弓网受流稳定性的基础上,减小受电弓的气动阻力,同时尽量避免对列车外形进行改造,是高速受电弓减阻问题中的难点和挑战。基于上述背景,本文针对新型单滑板高速受电弓,通过计算流体力学方法,得到受电弓各部件的气动阻力,分析受电弓不同部件的气动阻力占比,确定滑板与底座是气动阻力的主要来源,结合现有减阻优化方案,提出了不改变原有受电弓与车体结构的滑板减阻外壳与底座减阻外壳优化方案,并对减阻效果进行验证。

1 高速受电弓气动计算模型

为了准确获取受电弓的气动性能,本文基于某型高速受电弓和标准动车组的真实模型,进行模型简化与网格划分,进行数值仿真计算。

1.1 几何模型

受电弓的真实模型有大量的螺栓、垫片等微小结构,如果不进行简化,会极大增加网格数量,造成计算资源浪费。在划分网格前,在不改变原有主体结构的尺寸与构型的前提下,对受电弓进行模型清理与简化,得到气动计算简化模型(图1(a))。

图1 受电弓几何模型示意图Fig.1 Pantograph geometric model

为对比不同部件对于受电弓气动性能的影响,将受电弓整体分为弓头、上臂、下臂、上导杆、下导杆、底座和绝缘子七个部分,其中弓头细分为滑板、弓角、固定片、压簧和弓头其他五个部分(图1(b)),上臂自上而下细分为管轴、上交叉管、纵支柱、下交叉管和臂板五个部分,下臂自上而下细分为横铰、长杆和底部三个部分。

受电弓物面网格采用结构网格和非结构网格混合的方式,弓头结构精细,气流经过时流动复杂,采用结构网格,最小网格尺寸为1 mm；上臂杆、下臂杆和底座等较大尺度结构采用非结构网格,最大网格尺寸为20 mm。这种网格划分策略,兼顾了计算准确性与计算效率。

1.2 计算网格与边界条件

为尽可能模拟列车高速运行时受电弓周围的流场环境,计算区域依托标准动车组模型建立,流场大小为12 m×12 m×50 m,网格数2405 万,运行时受电弓实际安装位置如图2。围绕受电弓从近到远依次建立加密区、过渡区与远场区,边界层厚度为0.01 mm。除受电弓表面、车体表面与地面设置为无滑移壁面边界外,其余流场面均设置为流体穿透边界,以期实现流场的充分发展。

图2 车顶流场模型示意图Fig.2 Computational domain of train model

2 高速受电弓气动仿真控制模型设置

2.1 仿真运行工况

由于受电弓的现役速度主要为300 km/h,最高服役速度为350 km/h,与线路实验最大时速相比,仍有较大的提速空间,且目前对于高速运行状态下受电弓的气动减阻问题研究较少。本文选取300 km/h,350 km/h,385 km/h,400 km/h 和450 km/h 为典型运行速度,计算受电弓开口、闭口运行时的气动力。

2.2 仿真控制模型

尽管经过适当地简化,对于计算流体力学,高速受电弓的结构仍十分复杂,采用直接数值模拟与大涡模拟的方法,耗费计算资源过大,雷诺平均方法因其计算量小、计算精度高而广泛应用于工程实践。由于本文主要关注气动力的计算结果,对细微的流场细节不做重点关注。因此,本文采用雷诺平均方法进行数值仿真计算,湍流模型选择k −ε模型。采用CFD++ 软件,以定常计算的方式,每个算例迭代1000 步,使流场充分发展,保证计算结果的收敛性[15-17]。

由于计算速度处于300～450 km/h 之间,其对应马赫数在0.245 1～0.367 6 之间,为尽可能真实模拟实际运行状态的气动力,提高仿真计算精度,当速度小于350 km/h 时,采用三维不可压缩黏性理想气体进行模拟；速度大于等于350 km/h 时,考虑气体可压缩效应,采用三维可压缩黏性理想气体进行模拟。

3 高速受电弓气动阻力分析和优化部件确定

3.1 气动阻力分析

在对原始模型进行气动性能分析时,分别计算了300 km/h, 350 km/h, 385 km/h, 400 km/h和450 km/h 五个运行速度下的气动阻力。计算结果表明,不同运行速度时受电弓表面及周围空间的压力分布与不同部件的气动阻力占比呈现一定的相似性。因此,选取运行速度为385 km/h 时的计算结果为例进行分析(图3 和图4)。

图3 受电弓表面与中截面压力云图(续)Fig.3 Pressure distributions on the pantograph surface and at the center longitudinal plane of the pantograph (continued)

图3 受电弓表面与中截面压力云图Fig.3 Pressure distributions on the pantograph surface and at the center longitudinal plane of the pantograph

分析受电弓的表面及周围空间的压力分布,弓头、底座、交叉管、上臂横铰、下臂横铰、下臂底部、绝缘子迎风侧表面及附近压力相对较大,背风侧表面及附近压力相对较小,这些部件前后产生较大的压差阻力,是气动阻力的主要来源。

分析不同部件的气动阻力占比。

(1) 运行方向、运行速度对气动阻力占比

同一运行方向、不同运行速度时,各部件的气动阻力占比相近；同一运行速度、不同运行方向时,弓头、下臂的气动阻力占比几乎不变,上臂的气动阻力占比在闭口时增大,底座、绝缘子的气动阻力占比在闭口时减小。

(2) 不同部件的气动阻力占比

弓头、上臂、底座、绝缘子和下臂的气动阻力占整弓气动阻力的比值较大,占比从大到小排序依次为弓头、底座、上臂、绝缘子、下臂；上导杆和下导杆的占比较小。

由此可见,在受电弓运行时,滑板和底座会产生较大的气动阻力,应对其进行减阻优化。

3.2 优化部件选择

滑板处于受电弓顶部,是受电弓气动阻力的主要来源之一,气动阻力值约占受电弓整体的21%,减阻优化空间最大。滑板原始结构为中间宽、两边窄的变截面梁结构,截面为矩形,开口、闭口运行时表面直接迎风。滑板中间为接触段,两端为转角段,其间为过渡段。由于滑板矩形截面的流线度差,阻力系数大,气流经过时,迎风侧阻滞气流,背风侧发生流动分离,产生很大的压差阻力。为减小滑板的气动阻力,应对其采用流线化的外形优化。但是,受电弓运行时,滑板接触段上表面与接触线保持接触,倘若直接将截面上部修改为流线型,势必会减少滑板上表面与接触线的接触长度,降低列车受流质量；且滑板上层为石墨材料、下层为金属材料,直接加工成低阻力外形在工程上较难实现。因此,在不改变原有受电弓与接触网接触条件的前提下,在受电弓滑板截面两侧增加流线型导流外壳。这种设计,既可以增加截面流线化程度,又不会对原有受流质量与结构强度造成干扰,实际工程中也有较强的可操作性。

底座位于受电弓底部,其结构复杂,是受电弓升降弓与保持垂向稳定性的重要部分。受电弓底座构件繁多,结构复杂。气流经过此处时,发生复杂的绕流运动,各种旋涡不断生成和发展,彼此间发生强烈的耦合作用,最终形成强大的气动阻力,约占总阻力的26%。由于底座零件繁多,气流经过不同零件时相互耦合和干扰,倘若将其逐个优化,结构设计的工作量极大,同时气动性能较好的外形,是否满足原有结构强度和功能的要求,仍然需要大量的探讨。因此,本文尝试在受电弓原有底座上,加装底座减阻外壳,使其包裹原有结构,从而降低气动阻力。

4 部件减阻优化设计

4.1 滑板减阻

本文设计了三种不同构形的滑板减阻外壳,分别为圆形、椭圆形,以及NACA0012-20%形(图5(a))。建模时,对于圆形截面模型,滑板中间接触段圆直径为34 mm,两端转角段截面直径为24 mm；对于椭圆形截面模型,接触段椭圆短轴为34 mm,转角段短轴为24 mm,长轴短轴之比皆为3:2；对于NACA0012-20% 模型,取NACA0012 翼型的前缘20% 部分,接触段和转角段的原垂向边界为垂向最大宽度位置,垂向最大宽度分别为34 mm 和24 mm,三种方案的过渡段截面都为两端的线性过渡[18]。将三种截面形状的滑板,安装于受电弓实际位置上,进行气动阻力仿真计算,计算时,为节约计算资源,只对弓头进行计算(图5(b))。

图5 滑板减阻方案示意图Fig.5 Aerodynamic drag reduction scheme of contact strip

加装导流外壳后,气流流经滑板表面时,流动分离现象明显减弱,滑板前后的高压区与低压区均有所减小,压差阻力大幅下降。对比三种截面的减阻效果(表1),NACA0012-20% 构型的滑板减阻率最高,相比矩形截面时的弓头气动阻力,开口、闭口运行时整弓气动阻力分别降低17.07% 和18.61%。

4.2 底座减阻

针对底座部分,本文设计一种半椭圆形的外壳(图6(a))。其上表面为椭圆形,整体覆盖在底座和下臂底部之上,同时预留下臂转动的空间；下表面与原有轮廓平行,同时在前部设计一个流线型凸起,凸起处形状由半椭圆柱与两侧的1/4 纺锤体拼接而成,用以包裹气囊下部。设计时,为满足工程实现的可操作性,在与原底座之间周围,预留1～2 cm 的余量,以免结构过于紧凑,无法安装。将优化设计的底座进行气动性能计算,为节约计算资源,在车顶流场模型中,只对底座、绝缘子、下臂和下导杆进行计算(图6(b))。结果表明,相比于四个部件的原气动阻力值,包裹减阻外壳后,开口、闭口运行时整弓气动阻力分别降低10.45% 和4.94%。

图6 底座减阻方案示意图Fig.6 Aerodynamic drag reduction scheme of base

4.3 滑板底座综合减阻

基于前述工作,本节将NACA0012-20% 滑板模型与底座减阻模型结合,分析两种方案的综合减阻效果(图7)。

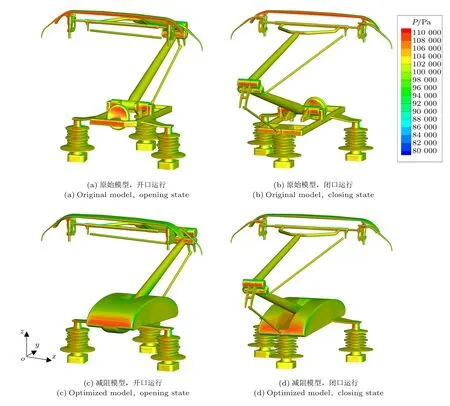
图7 受电弓减阻模型对比图Fig.7 Comparison between original model and optimized model

对比不同运行速度和运行方向情况下的减阻效果(表2),相比于原模型,不同运行速度下,整弓气动阻力的减阻效果相近,随着速度增加,减阻效果略微减小。开口运行时,整弓气动阻力降低24.74%～25.13%,闭口运行时,整弓气动阻力降低23.50%～24.19%,均实现了较大程度的减阻效果。

表2 不同运行速度和运行方向情况下减阻效果Table 2 Aerodynamic drag reduction effect in different conditions

5 结论

通过计算流体力学方法,对受电弓进行气动计算,并对受电弓各部件的气动阻力和空间压力云图进行分析,明确滑板与底座是受电弓气动阻力的主要来源。在不改变受电弓和车体原有结构的基础上,提出了NACA0012-20%滑板截面优化与半椭圆形底座减阻外壳优化方案,计算表明,350 km/h 典型运行速度下,减阻模型在开口、闭口运行时整弓气动阻力分别降低可达25.13% 与24.19%,取得了明显的减阻效果。