6DOF焊接机器人运动学分析及仿真

宁青杰，施立品，唐 兵，张宝宁

（中国矿业大学（北京）机电与信息工程学院，北京 100083）

1 引言

液压支架结构件尺寸大，多为拼焊而成的箱型结构件，需要由多个小跨度焊接机器人同时焊接，作业效率较低[1]。随着大采高开采以及深部开采的煤矿的日益增多，液压支架面临着更加严峻的考验，其失效的可能性不断上升，机械设备需要更高的可靠性。液压支架承受重载和冲击的主要零部件多由中厚板材焊接而成的箱型结构件组成。液压支架的强度直接影响煤矿安全生产［2］。

机器人的智能化促进了焊接技术的不断创新[3]。焊接机器人不仅能够高质量地完成焊接任务，而且也能代替工人完成既危险又复杂的高强度工作，从而节省人力资源，降低生产成本，在国内外均有着广阔的应用前景。通过仿真，可节省优化焊接轨迹所用的时间，提高焊接效率，满足生产需求[4]。机器人末端手腕（TCP）所能到达的工作区域以及角位移、角速度和角加速度的连续性是衡量焊接效率、精度和质量的重要指标[5]，是焊接机器人设计、运动学分析和运动控制过程中亟待处理和解决的关键性问题。

在求解机器人工作空间的多种方法中，数值法的应用最为广泛。蒙特卡洛法[6]是一种数值分析方法，在多于三自由度的机器人研究中，通常用于求解其工作空间[7]。采用数值分析方法，通过调用Robotics Toolbox工具箱中的5次多项式jtraj函数，对关节空间PTP轨迹规划进行仿真分析研究。

2 焊接机器人正运动学分析

液压支架焊接机器人是专门针对液压支架大型结构件的焊接任务所配备的专用工业机器人，以六自由度串联机器人居多。焊接机器人SR165的空间结构图，如图1所示。

图1 焊接机器人SR165的空间结构图Fig.1 Space Structure Diagram of Welding Robot SR165

2.1 建立连杆坐标系

焊接机器人SR165由多个关节轴和连杆组成，在三维空间中实现多自由度运动。用ai、αi、di和θi四个参数来描述相邻两杆之间的相对关系[8]，分别称为连杆长度、连杆扭角、连杆偏距和关节转角，如图2所示。

图2 连杆关节轴关系图Fig.2 Connecting Rod Joint Axis Diagram

建立相对应的坐标系后再进行相互转换，可得焊接机器人SR165末端焊枪的位姿。这种用连杆参数表达机械机构运动的方法称为Denavit−Hartenberg参数法[9−10]，简称D−H参数法。

2.2 正运动学模型建立与求解

2.2.1 正运动学建模

焊接机器人末端焊枪的位置和姿态由连杆运动链相邻连杆的运动状态叠加而成，通过D−H参数法进行描述。假设杆1相对于基坐标的位姿表达为，那么杆i相对于基坐标的最终位姿就是前面相邻齐次变换矩阵相乘后的积。

式中：[n o a]—姿态向量；

P—位置向量。

在串联的运动链中，相邻两连杆之间的广义变换矩阵如下：

式中：αi−1—连杆扭角；ai−1—连杆长度；θi—关节转角；di—连杆偏距。

机器人SR165以垂直关节居多，采用经典D−H参数法建模，以下为机器人各关节的运动简图，如图3所示。

图3 机器人SR165关节运动简图Fig.3 Robot SR165 Joint Motion Diagram

从图3可知，前、后三个关节分别决定了焊接机器人SR165前端的焊枪在工作空间中的位置和姿态。

根据D−H 参数法，确定相邻坐标系之间的变化转换关系。焊接机器人SR165的D−H参数，如表1所示。

表1 机器人SR165 D-H参数Tab.1 D-H Parameters of Robot SR165

2.2.2 正运动学求解

根据机器人设计值确定出四个连杆参数，代入公式（3）即可求得相邻两杆之间的位姿变换矩阵：

式中：cθi=cos(θi)；sθi=sin(θi)；cαi−1=cos(αi−1)；sαi−1=sin(αi−1)。分别带入αi−1、ai−1、θi和di，可得转换矩阵分别为

上面每一个相邻杆件的变换矩阵都是关于转角θi的函数，把带入参数的六个变换矩阵依次相乘计算出四阶的位姿变换矩阵，若六个转角θi值已知，便可确定末端焊枪位姿，转换矩阵如下：

式中：[nx ny nz]T、[ox oy oz]T、[ax ay az]T—机器人SR165焊枪末端姿态坐标向量；[px py pz]T—位置坐标向量。通过MATLAB的求解运算获得变换矩阵，这个（4×4）矩阵中的12个元素分别为：

式中：c23和s23是cos（θ2+θ3）和sin（θ2+θ3）的简写，其中i，j=1…6。

3 焊接机器人逆运动学分析

3.1 逆运动学代数求解

上节通过建立焊接机器人SR165正运动学模型，计算出（4×4）阶的转换矩阵，把已知各关节的实际旋转角度值代入正解方程，即可得到机器人SR165末端焊枪的位姿。

用齐次矩阵形式建立机器人SR165数学模型，用矩阵法计算机器人的逆解，六个关节角的求解过程如下。

3.1.1 求解θ1

使方程（6）两边矩阵（2，4）元素分别对应相等可得：

计算可得：

θ1=atan()，易知θ1有唯一解。

3.1.2 求解θ2

使方程（8）等式两边矩阵（1，4）和（2，4）元素对应相等可得：

移项，方程（10）变为下式：

令k1=c1rx+s1ry，

方程（10）和（11）两边平方后分别对应相加可得：

易知θ2有两个解。

3.1.3 求解θ3

式（11）中：令k3=c2(c1rx+s1ry)−s2rz−a1c2−a2

3.1.4 求解θ4、θ5

使方程（13）等号两边矩阵（1，3）、（2，3）和（3，3）元素分别对应相等可得：

由式（14）和式（16）可得：

由（15）可得：θ5=±arcos(−r33c23−c1r13s23−r23s1s23)

易知θ4有唯一解，θ5有两个解。

3.1.5 求解θ6

使方程（13）等式两边矩阵（2，1）和（2，2）元素分别对应相等可得：

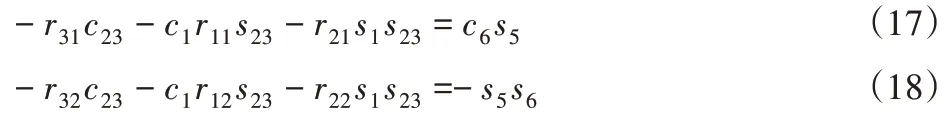
联立式（17）和式（18）可得：

综上所述，对于焊接机器人SR165的同一种位姿，共有8种可能的关节角度组合。

4 SR165焊接机器人工作空间分析

4.1 6DOF焊接机器人工作范围分析

运用集合的概念，焊接机器人SR165的工作空间为其末端焊枪所能到达的三维空间中所有点的集合，其工作空间的数学表示，如式（19）所示。

4.2 蒙特卡罗法工作域分析

蒙特卡罗法是一种可用于求解机器人工作空间的基于随机概率的数值法。用该方法求解机器人的工作空间可分为以下四个步骤：

（1）由正运动学方程可得末端点的位置向量如下：

式中：a1=350mm；a2=1100mm；a3=260mm；d4=1110mm。

（2）确定各关节的转角范围，调用MATLAB中的随机值函数RAND（），用最大转角减去最小转角后与RAND（）函数相乘，即可得到各关节转角相对应的步长变量，即(−)×RAND()，从而可得各关节随机变量为：

（3）将式（21）中的六个随机变量分别带入到式（20）中的元素Px、Py和Pz中，即可得到焊接机器人SR165末端焊枪所能到达的所有空间点集。

（4）根据具体要求设置循环次数，通过MATLAB编程实现该算法，输出结果，实现工作空间仿真分析。以下为蒙特卡罗法步骤[12]，如图4所示。

图4 蒙特卡罗法步骤示意图Fig.4 Monte Carlo Method Steps

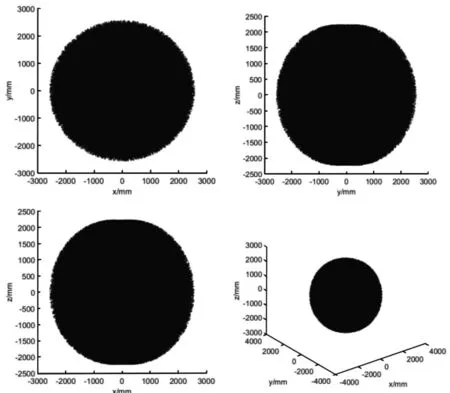
图5 二维及三维工作空间云图Fig.5 2D and 3D Workspace Cloud Map

从图5可知，焊接机器人SR165末端焊枪所能到达的区域与仿真工作空间的尺寸相对应，分布在各个投影面上的随机点组成的云图较均匀，没有明显空洞现象。焊接机器人SR165工作空间云图形状紧凑，MATLAB仿真结果与实际工作空间相一致，能够满足大范围跨度钢件的焊接要求。

5 6DOF焊接机器人末端轨迹规划

空间轨迹规划包括关节空间规划与笛卡尔空间规划[14]，两种轨迹规划各有优缺点。充分利用两种规划的优点，使其末端既能到达指定的位置又能使其末端轨迹连续平滑，5.1节中使用MAT‐LAB软件对焊接机器人SR165进行建模，并分别对两种规划进行仿真分析。

5.1 6DOF焊接机器人MATLAB三维建模

使用Robotics Toolbox 工具箱，对焊接机器人SR165进行三维建模，调用SerialLink函数将六个连杆连接起来构成一个运动链，生成的机器人SR165模型，如图6所示。调用teach函数弹出机器人关节驱动器，可以通过调节或键入弧度值实现机器人驱动效果，如图7所示。通过滑动滑块即可将机器人末端焊枪运动到指定的位姿。

图6 焊接机器人在qA状态下的三维图Fig.6 3−D Diagram of the Welding Robot in qA State

图7 焊接机器人驱动调节器Fig.7 Welding Robot Drive Regulator

5.2 关节空间轨迹规划

调用Robotics Toolbox 工具箱中的q=jtraj（qA，qB，t）函数，其中分别表示各个关节的起点和终点的角度，默认的起点和终点速度均为零［3］。使用画图命令plot可以得到焊接机器人在qB状态下的三维图，如图8所示。使用画图命令plot3可以得到焊接机器人在qB状态下末端轨迹图，如图9所示。

图8 焊接机器人在qB状态下的三维图Fig.8 3−D Diagram of the Welding Robot in qB State

图9 焊接机器人末端轨迹Fig.9 End Trajectory of Welding Robot

为了在关节空间中规划机器人的运动轨迹，需要设定运动起点与终点，取起点qA=［0 −pi/2 −pi/2 0pi/2 0］，终点qB=［pi/2pi/3 0−pi/6 −pi/3 −pi/2］，运动时间设定为10s，分别对六个关节进行仿真分析研究。

调用jtraj函数对焊接机器人SR165关节空间进行5次多项式插值，调用plot中的q、qd和qdd函数，得到各关节的角位移、角速度和角加速度随时间变化的曲线图，分别如图10、图11和图12所示。

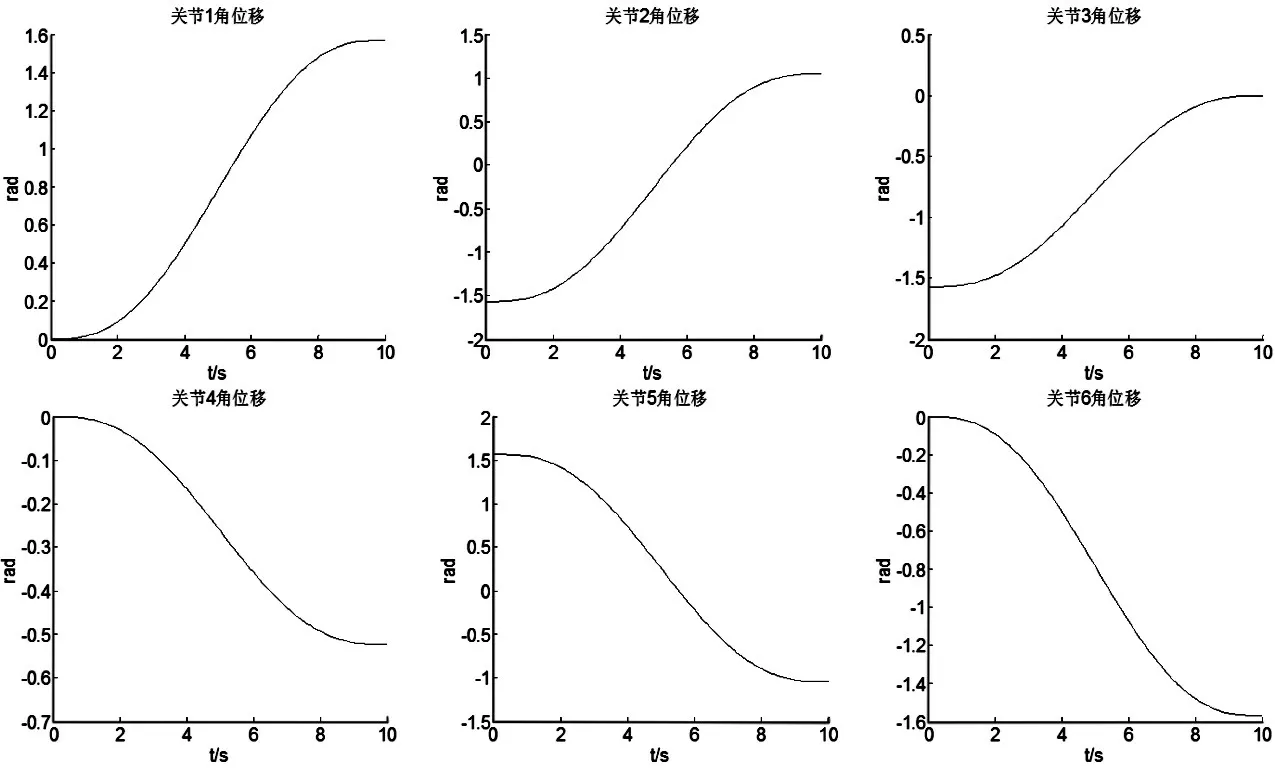
图10 各关节角位移曲线Fig.10 Angular Displacement Curve of Each Joint

图11 各关节角速度曲线Fig.11 Angular Velocity Curve of Each Joint

观察图10~图12中曲线，可知机器人SR165在运动过程中角位移、角速度和角加速度曲线光滑平稳，无突变位置，说明机器人各个连杆之间没有发生错位的现象，角位移从起点随着时间的推移运动到终点，各关节的角位移均未出现突变现象。

图12 各关节角加速度曲线Fig.12 Angle Acceleration Curve of Each Joint

关节1、2、3的角速度前5s逐渐上升，5s时达到最大速度，后5s逐渐下降为零，关节4、5、6的角速度恰好相反。

各个关节角加速度先正后负与其各关节速度先增大后减小相对应，因此该关节空间轨迹规划是合理的。

5.3 笛卡尔空间轨迹规划

以直线为例进行笛卡尔空间轨迹规划，取起点T1=transl（378.16，1753.39，1023.82），终点T2=（587.932，1720.327，880.306），运行时间设为10s，调用Robotics Toolbox 工具箱中的五次多项式函数ctraj，对机器人SR165进行运动轨迹规划，调用plo（tt，T（j：，i））函数可得出机器人SR165末端焊枪在10s内连续的空间坐标，如图13所示。

图13 机器人末端三维空间坐标Fig.13 3−D Space Coordinates of the Robot End

通过调用程序语句plot3（T（j：，1），T（j：，2），T（j：，3））可得出机器人SR165末端焊枪在工作空间中的直线运行轨迹，如图14所示。

图14 机器人末端空间运动轨迹Fig.14 Robot End Space Motion Trajectory

为了确定该直线轨迹规划是否合理，通过仿真得出机器人SR165运动过程中转角的变化范围，运行程序可得各关节转角的变化曲线，如图15所示。

图15 各关节角度变化曲线Fig.15 Angle Change Curve of Each Joint

焊接机器人实物图，如图16所示。

图16 焊接机器人实物图Fig.16 Welding Robot Physical Picture

6 结论

（1）使用MATLAB 软件编写程序，仿真分析了焊接机器人SR165的工作空间，结果表明，焊接机器人SR165工作空间范围跨度大，能满足大空间焊接钢件的要求，与期望可达工作区域相符。

（2）采用两种轨迹规划方法进行仿真分析，结果表明，焊接机器人SR165末端焊枪运动时的角位移、角速度和角加速度曲线连续、平滑，均未出现突变现象，使得中厚板结构件焊接能够高质量地完成大范围跨度和无突变性焊接的任务。

（3）通过对焊接机器人SR165进行运动学分析，保证了箱型结构件的焊接效率、精度和质量，液压支架的安全性得到进一步提升，对现代智能化采煤有着极其重要的基础意义，为后续SR165焊接机器人动、静力学及运动控制分析研究奠定了一定的理论基础。