应用有限单元法耐高压观察窗疲劳寿命分析

王素粉

（1.河南科技大学应用工程学院，河南 三门峡 472000；2.三门峡职业技术学院机电工程学院，河南 三门峡 472000）

1 引言

耐高压观察窗是深海潜水装备的重要组成单元，是观察外部环境的重要窗口，根据工作环境的特点，将承受较大的压力冲击[1]。

由于观察窗在反复升降过程中，受海水循环扰动力作用会产生裂纹，甚至发生断裂，疲劳破坏会带来灾难性后果，危害装置安全，所以对观察窗进行疲劳分析具有重要的意义，而引起失效的循环载荷往往小于根据静载荷强度分析的“安全”载荷，因此，传统的静强度分析不能解决疲劳问题。因此，根据不同的损伤理论对观察窗进行分析具有重要的意义。

学者们进行了一定研究：文献[2]基于软件建模分析连接形式对观察窗用材的影响，并获得了最优的设计；文献[3]基于多种分析方法对承受高压的装置结构性能和极限载荷进行分析，并对装置的稳定性进行分析；文献[4]基于观察窗属于有限寿命的设计，采用不同的寿命预测方法，针对耐高压观察窗的结构参数和使用环境进行设计，并对比预测结果的可靠性；文献[5]基于疲劳损伤理论，分析随机载荷对疲劳寿命的影响，并对寿命进行了预测，将预测结果与试验分析进行对比。基于锥台式观察窗的结构特点，对观察窗的疲劳载荷和所受的液动力进行分析；基于观察窗载荷谱和有机玻璃的S−N曲线，进行有限单元法建模仿真分析，并根据Miner线性累积损伤理论公式，分析观察窗的疲劳损伤，获得使用寿命；搭建观察窗压力试验装置，获得观察窗压力载荷作用下的轴向位移，根据蠕变损伤模型获得疲劳寿命，验证仿真分析的可靠性。

2 观察窗疲劳分析和计算

2.1 观察窗结构

锥台式观察窗具有良好的力学性能，能够承受最高200MPa的海底高压，同时具有良好的密封性，而被广泛应用[6]，结构，如图1所示。

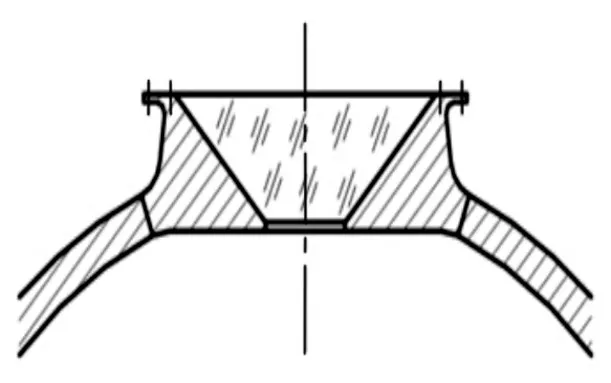
图1 锥台形观察窗结构示意图Fig.1 Schematic Diagram of the Frustum−Shaped Observation Window

2.2 观察窗疲劳载荷

疲劳发生的外部原因是扰动力，即随时间变化的应力。通常以载荷（N）−时间（T）变化的图或表来描述载荷的变化，称之为载荷时间历程即载荷谱[7−8]。首先，对观察窗的下潜深度、平均速度、次数等进行分析，获得压强P、次数n的数据，最后分析和计算载荷谱。统计设备5次下潜数据统计，如表1所示。在计算下潜的过程中受到的最大压强时，海水密度取1.025g/cm2[9]。根据记录，计算最大深度的压强，即观察窗受最大压强，下潜过程以匀速下潜，平均速度为40m/min。

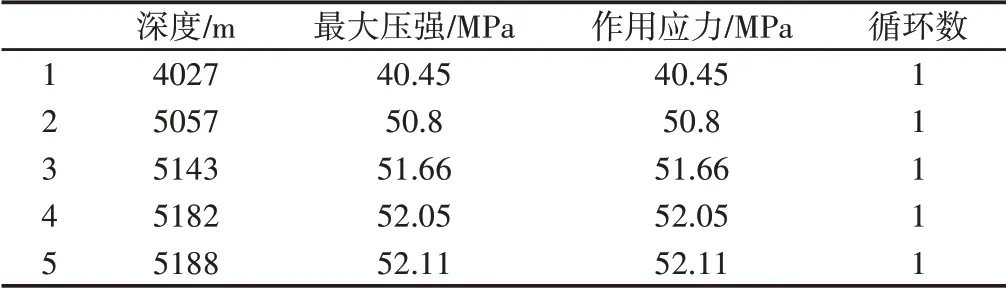
表1 数据分析Tab.1 Data Analysis

2.3 观察窗受液动力分析

当波浪和海流经过时，会对设备整个系统产生一个力，称为液动力。液动力主要由于拖拽力和惯性力导致。简单的说一个是由于水的速度引起的，一个是由于加速度引起的[10]。

系统的坐标定义如下：Z轴为垂直水面方向，沿着水深的反方向为正。X轴的正方向为海流方向，X−Y平面为水平面，设观察窗任意一点的深度z处取一微分dz，根据莫里森（Morison）方程，该段的波力为：

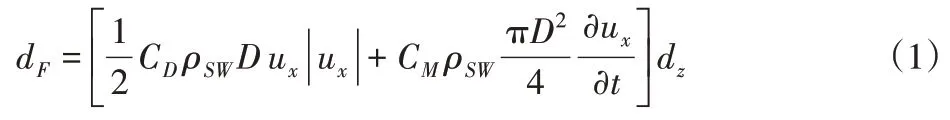
式中：CD—阻力系数；ρSW—海水密度；D—直径；ux—水质点的水平速度；CX—惯性力系数；水质点水平加速度。

对式（1）进行修正，设速度矢量uc与x轴的夹角为ψ，该矢量在三个坐标轴上的投影为{uccosψ，ucsinψ，0}，则观察窗上的力的矢量为：

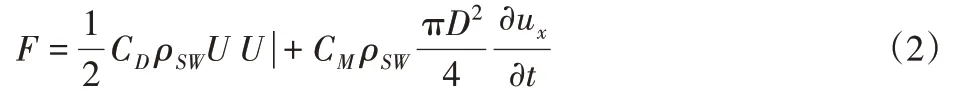
式中：U=e×（u总×e），u总=u+uc，e—沿着水深的单位矢量。

用下式来模拟海流流速随深度变化的关系：

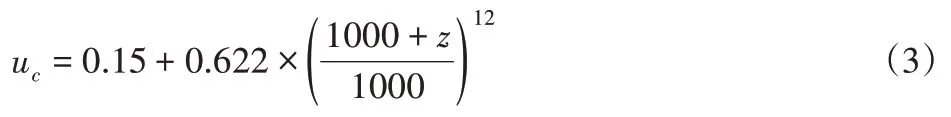
其变化趋势，如图2所示。

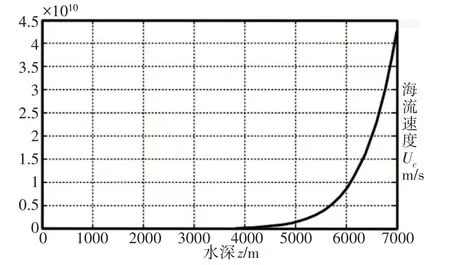
图2 海流流速随深度变化的曲线Fig.2 Curve of Sea Current Flow Rate as Function of Depth

取海流方向与波浪的传播方向一致，根据修正后的Morison方程，作用在扬矿管水深（z2−z1）上的水平波力的大小为：

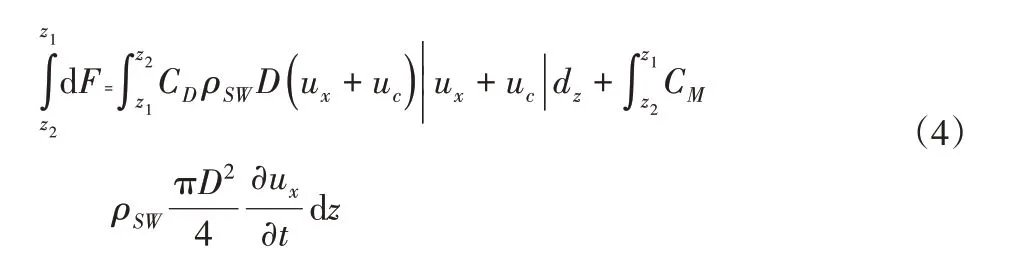
从上式可以得出，利用Mrison方程计算液动力，主要因素为波浪波面的高度、水质点的水平速度和水平加速度。并且要计算得出拖拽力系数和惯性力系数[11]。拖拽力系数与雷诺数Re、Kc数及表面粗糙度有关。

根据试验数据得出CD=1.2。惯性力系数取CM=2.0。

水平速度和水平加速度的表达式可简化为：

运用Mapel软件对上述公式进行计算，得到曲线图。液动力随着深度变化而变化的曲线，如图3所示。

图3 液动力随着深度变化而变化的曲线Fig.3 Curve of Hydraulic Dynamics as a Function of Depth

观察窗在下潜的过程中还受到海水压力的作用，每一千米的受压为10MPa，得到压力作用的大小。将海水液动力和海水的压力作用合成得到以下的观察窗的总受力图，如图4所示。

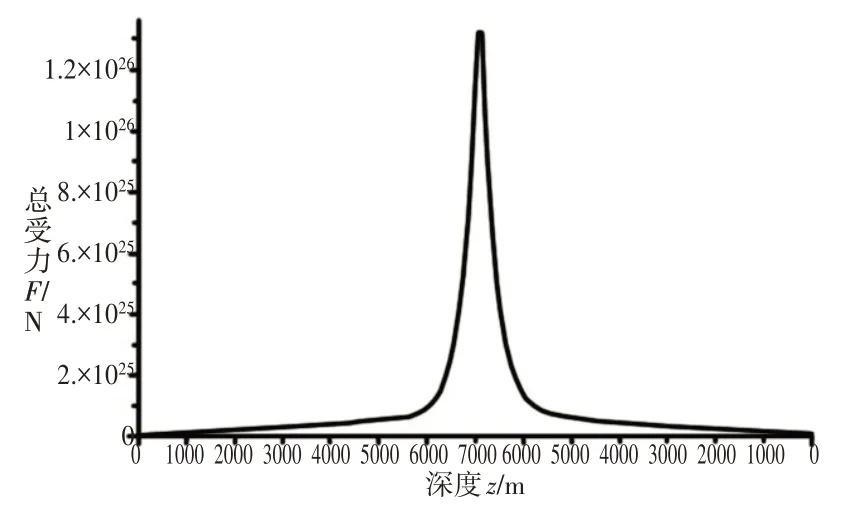
图4 观察窗总受力Fig.4 The Total Force of the Observation Window

从图中可以看出观察窗的总受力呈曲线上升且对称分布，为后续的疲劳分析提供加载数据。

3 观察窗全寿命预测

3.1 Miner线性累积损伤理论

构件在应力水平Si作用下，经受ni次循环的损伤为Di=ni/Ni。若在k个应力水平Si作用下，各经受ni次循环，则可定义其总损伤为：

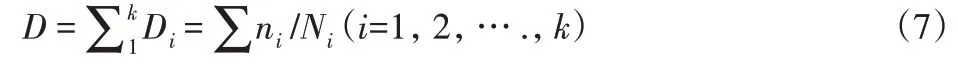
破坏标准为：

3.2 计算各载荷下的疲劳寿命Ni

将整个耐高压观察窗的三维模型导入Ansys界面，为了简化模型，导入Geometry−Design Modeler 界面，对装配体进行对称面约束的设置，将模型简化为四分之一模型。按照材料参数，定义有机玻璃和碳结构钢的材料参数，将有机玻璃与装配体接触面的联接方式设置为frictioness，且摩擦系数设为0.3，定义加载的载荷，如表1所示。并定义有机玻璃的S−N 曲线，有机玻璃的S−N曲线，如图5所示。在输出结果一栏选择Fatigue Life，进行疲劳寿命的有限元的计算。

图5 有机玻璃S−N曲线Fig.5 Plexiglass S−N Curve

选择Fatigue Tool工具中的Life，计算观察窗的疲劳寿命。首先模拟下潜7000m 的情况，加载情况模拟海底受载情况，下潜7000m，受海水压力的变化是从0MPa—70MPa—0MPa，同时考虑液动力的作用，将合力编写成加载.DAT文档，输入ANSYS软件当中，得到相应的加载曲线，如图6所示。

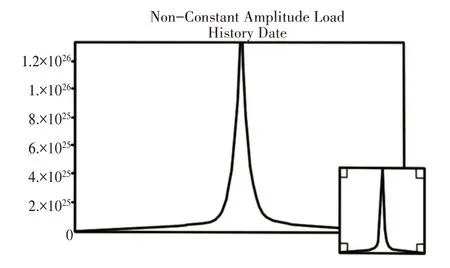
图6 载荷块幅值为70MPa的加载曲线Fig.6 Load Curve of Load Block Amplitude 70MPa

运行结果显示此载荷下，观察窗的疲劳寿命3.9289e5Circle，即可进行此加载3.9289e5次。

3.3 基于Miner线性积累损伤理论全寿命计算

对观察窗按照载荷谱，进行5次加载，载荷的大小见载荷谱表1，采用有限元的方法计算观察窗的疲劳寿命Fatigue Life，其加载方法、材料的参数设置、接触设置及网格划分与应力应变分析操作相同，分析得到的观察窗在相应载荷下的寿命图，如图7所示。

图7 不同深度下的寿命分析Fig.7 Life Analysis at Different Depth

根据图中的疲劳寿命云图，可以看出观察窗寿命最小值点，即危险点的位置。

表2 观察窗载荷（S）-寿命（N）数据表Tab.2 Observation Window Load（S）-life（N）Data Sheet

根据表中分析数据，可得计算结果为：

由Miner线性积累损伤理论可以判定观察窗没有发生疲劳破坏，并且经过计算得到观察窗的疲劳寿命为：n=1/D=21359 Cir‐cle。即进行相同载荷的五次加载可以使用21359次。

4 试验分析

为真实模拟高压观察窗的工作环境，搭建的试验压力装置，如图8所示。采用球形结构的压力装置的应力较小，此结构适用于超高压力容器。

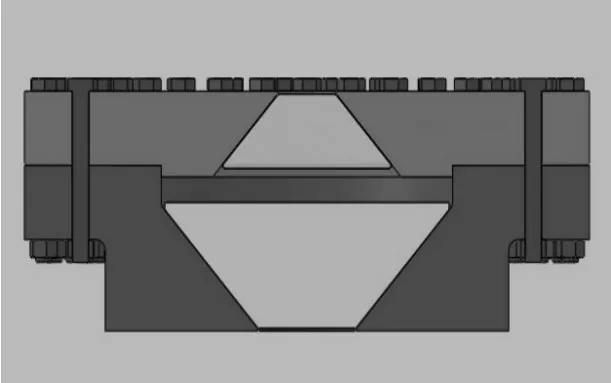
图8 压力试验装置Fig.8 Pressure Test Device

根据表1所示的5种压力，对装置进行保压试验，达到设定压力值，保压10min，待装置稳定后，测量观察窗的轴向位移，每个压力值进行三次重复试验结果，如表3所示。

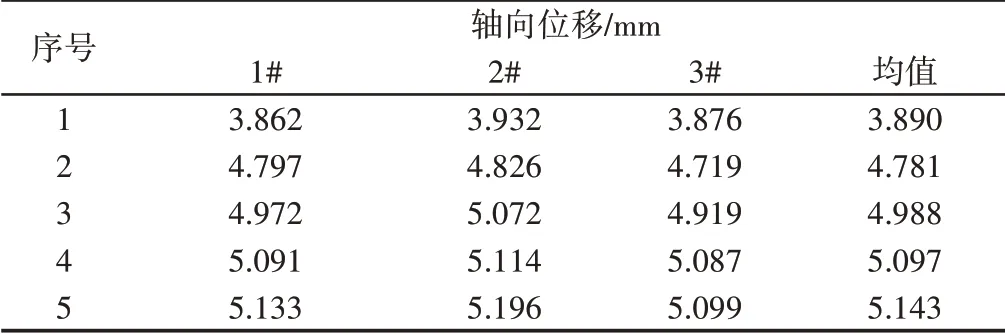
表3 观察窗轴向位移Tab.3 Axial Displacement of the Observation Window

由试验数据可知，最大轴向位移蠕变量为1.253mm。根据蠕变疲劳损伤模型，累积损伤等于疲劳损伤增量和蠕变损伤增量线性相加。

即：

对模型进行积分可得蠕变疲劳损伤演变方程：

对式（13）自N=0，Dcf=0到N=Ncf，Dcf=1积分得：

其中：

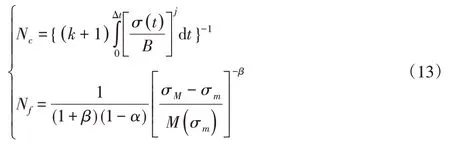
将参数代入，可得：Ncf=21326 Circle，而仿真获得的疲劳寿命为21359 Circle，二者误差为1.5%，两种方法分析结果误差较小，可认为基本一致。

5 结论

针对耐高压观察窗的疲劳寿命进行分析，采用模型仿真和试验分析两种方法进行对比分析，结果可知：

（1）基于观察窗载荷谱和有机玻璃的S−N曲线，进行有限单元法分析，基于Miner理论公式，计算观察窗的疲劳损伤，获得使用寿命为21359 Circle；

（2）基于试验装置和蠕变损伤模型，对观察窗的疲劳寿命进行预测分析，得到使用寿命为21326 Circle；

（3）仿真与试验结果误差在1.5%，二者基本一致，表明模型仿真的可靠性和准确性。