七自由度车−路耦合模型设计及试验研究

苏 鸣，李 硕，黄 浩，刘 依

（1.武汉科技大学机械自动化学院，湖北 武汉 430080；2.武昌首义学院机电学院，湖北 武汉 430070；3.武汉东湖学院机电学院，湖北 武汉 430070）

1 引言

近十几年来，我国国民经济的飞速发展，汽车的保有量不断增加，车辆超载、超速行驶对路面造成破坏已经成为普遍现象。车辆在行驶时因为路面不平整、车体结构和行驶状态的影响，车辆对路面的载荷会出现动态变化，这种变化通过动轮胎力传递到路面，形成动载荷并导致路面受到的实际载荷要大于静态载荷[1−2]。

国内最先是由文献[3]提出了车辆与路面间的动力响应问题；文献[4]，建立了车辆在路面不同等级路面激励下的动态响应模型；文献[5]，设计了二自由度1/4车−路耦合试验模型，首先通过模型试验方法研究1/4车辆模型对路面的动力响应。

文献[6]，通过实际检测路面的变形情况对动载荷进行了分析，存在试验成本高，工期长，试验结果不具备广泛性。

综上所述，利用模型试验对车−路间动力响应进行规律性试验是研究的趋势。

国内目前在动载模型试验研究方面只基于二自由度1/4模型，无法实现前后轮动载情况的对比研究。基于此，这里以七自由度车−路耦合动力学模型为基础，进一步构建了四轮七自由度车−路耦合模型试验装置，通过静动态试验对车−路间动载荷进行规律性研究。

2 七自由度车−路耦合数学模型

对车辆的动载分析必须建立恰当的车辆动力学模型。因为车辆在实际状况下是一个十分复杂的振动系统，为了建立简化的数学模型，需要提出必要约束条件：假设车辆在路面作匀速直线运动，采用四轮布局前后轮处于同一行进线上且车轮始终与路面接触；考虑前后轮与左右轮间的相干性；车辆质心位置不变；车辆沿x轴侧倾角度与y轴俯仰角度均小于5度；忽略车轮阻尼。

建立七自由度整车模型，如图1所示。模型参数，如表1所示。

图1 七自由度整车模型Fig.1 7−Full Vehicle Model

表1 车辆模型参数Tab.1 Vehicle Model Parameters

图中：W1,W2,W3,W4— 四个车轮受到的路面激励；Xt1,Xt2,Xt3,Xt4—四个车轮的垂直振动位移；Xz1,Xz2,Xz3,Xz4—四个车轮中心处车身端点的垂直位移。

根据振动系统拉格朗日方程，建立七自由度车辆模型垂直方向运动微分方程根据振动系统拉格朗日方程，建立七自由度车辆模型运动微分方程：

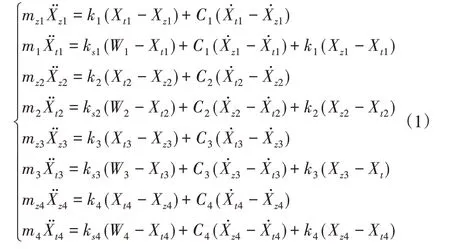
不同车轮由路面激励所产生的垂直动态力Ft为：

车辆引起垂直方向的振动包含静态力和动态力[7−8]，而动载Fd即车辆在路面激励下引发振动的静态力Fj与动态力Ft之和，即：

路面是车辆在行驶过程中产生振动的主要输入，用kelvin地基模拟路基，两端简支的有限长分度刚度板模拟路面[9]，如图2所示。

图2 路面模型Fig.2 Pavement Model

采用路面位移功率谱密度描述其统计特性，考虑车辆行驶速度v对振动系统输入的影响，由时间频率；ω—频率指数；n—空间频率。

引入下截止频率ω0，路面速度时间谱密度可采用幂函数形式作为拟合表达式[10]：

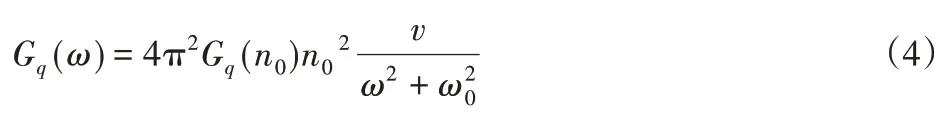
式中：Gq(ω)—路面不平度功率谱密度；Gq(n0)—路面不平度系数；n0=0.1m−1—参考空间频率；ω—频率指数。

利用滤波白噪声法[11]将速度时间功率谱密度函数转变为状态方程：

选用二阶Pade 算法，n=2，常数P2=1/12，则将公式（6）经过Laplace变换转化为状态空间方程得：

以路面时域激励W1(t)，W2(t)，W3(t)，W4(t)作为车辆模型的动态输入，运用MATLAB/Simulink建立七自由度车−路耦合仿真模型，截取部分模型为例，如图3所示。

图3 部分车轮动载仿真模型Fig.3 Part of the Wheel Dynamic Load Simulation Model

3 七自由度车−路耦合试验装置设计

装置整体设计包含车辆模型设计，路面模型设计，传动控制设计。要求车辆模型运行载荷、行驶速度可调，确保车辆运行稳定，便于对不同工况进行研究，装置设计方案，如图4所示。

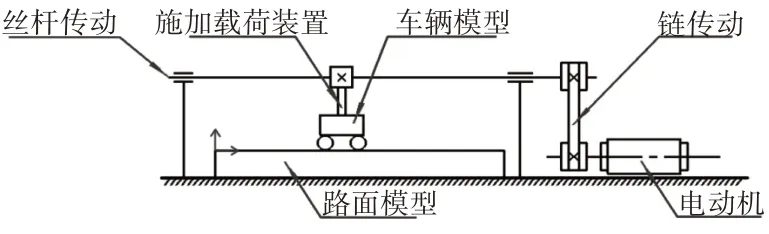
图4 试验模型方案Fig.4 Test Model Scheme

3.1 车辆模型

七自由度车辆模型由四组定向车轮，车体，载荷施加装置，导轨滑块组成，如图5所示。

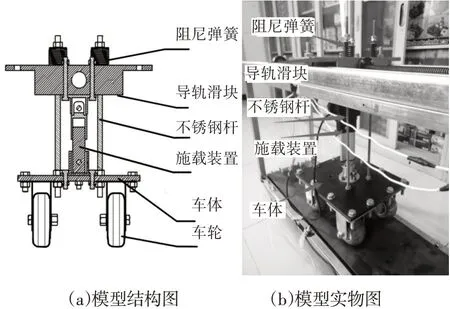
图5 车辆模型Fig.5 Vehicle Model

由于车辆悬架系统的复杂性，要求车辆悬架系统即不影响车体行驶稳定也不会影响对车轮振动的监测。设计将模拟悬架部分通过四根不锈钢杆连接车轮、车体以及导轨滑块，将阻尼弹簧安装至导轨滑块上端作为悬架阻尼，同时起到稳定车体的作用。

选用型号为Y80M2−2三项异步电动机作为动力输出，通过铰链丝杆带动模型前进。采用丝杆传动目的是保证传动平稳，减少冲击加速度对试验精度的影响。导轨滑块两端装有限位滑轮与导轨紧密连接，以固定导轨滑块位置，保持与车辆行进方向平行，同时保证车辆行驶稳定，降低车辆侧倾与俯仰程度，如图6所示。

图6 传动机构实物图Fig.6 Physical Diagram of Transmission Mechanism

3.2 路面模型

将弹簧均匀布置在底座上模拟Kelvin地基以支撑路面，弹簧上铺设匀制刚度板模拟路面，路面两端设计为简支结构通过螺栓与弹簧连接，路面高度可以通过两端螺栓调节，如图7所示。路面行程1500mm，宽300mm。

图7 路面实物模型Fig.7 Pavement Model

3.3 控制系统与数据采集

装置设计工况为车辆行驶速度（0.1~1）m/s，车辆载荷（包括车体自重）为（100~500）N，通过电动推杆调节。在车辆行驶路径始末装有光电开关，防止车辆在运行始末出现卡死，碰撞等情况。试验主要设备有CA−YD−186TE 压电式加速度传感器，精度100mV/g、D/A数据转换芯片、STM32F103数据采集处理芯片、电气控制柜和电脑等，如图8所示。

图8 数据采集部分Fig.8 Data Acquisition Section

4 仿真与试验分析

因路面的振动激励为低频，可忽略模型的高阶固有频率。通过对车辆模型的状态实验，测定车辆模型的低阶固有频率为3.91Hz，数值解为4.23Hz，频率误差为7%，证明模型设计合理，模型详细参数，如表2所示。车辆运行速度为0.1m/s，0.3m/s，0.5m/s，仿真车辆运行工况与试验运行工况一致。选右前轮与右后轮为测试对象，考虑前后轮的间干涉影响，仿真结果，如图9~图11所示。

表2 模型主要参数值Tab.2 Main Parameter Values of the Model

图9 前后轮0.1m/s动载仿真时域图Fig.9 Time Domain Diagram of Dynamic Load Simulation for Front and Rear Wheels at 0.1m/s

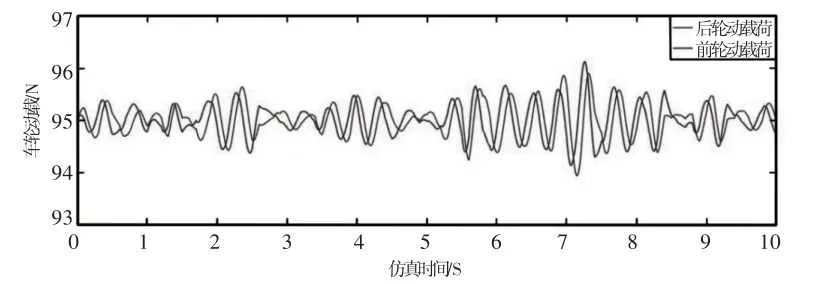
图10 前后轮0.3m/s动载仿真时域图Fig.10 Time Domain Diagram of Dynamic Load Simulation for Front and Rear Wheels at 0.3m/s

图11 前后轮0.5m/s动载仿真时域图Fig.11 Time Domain Diagram of Dynamic Load Simulation for Front and Rear Wheels at 0.5m/s

将传感器分别安装于右前后轮上，检测分析不同情况各轮胎的振动情况，根据式（3）计算出实际车辆运行动载荷，试验分析结果，如图12~图14所示。动载峰值统计，如表3所示。

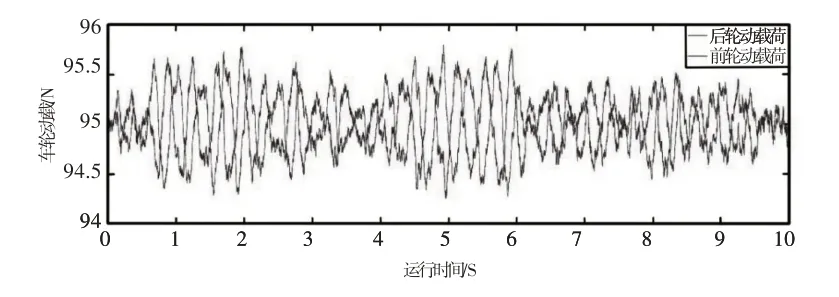
图12 前后轮0.1m/s动载试验时域图Fig.12 Time−Domain Diagram of Front and Rear Wheel 0.1m/s Dynamic Load Test

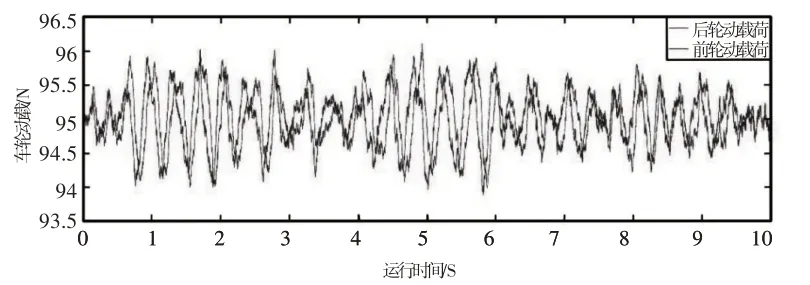
图13 前后轮0.3m/s动载试验时域图Fig.13 Time−Domain Diagram of Front and Rear Wheel 0.3m/s Dynamic Load Test

图14 前后轮0.5m/s动载试验时域图Fig.14 Time−Domain diagram of Front and Rear Wheel 0.5m/s Dynamic Load Test

表3给出了仿真与试验数据对比，数值解与试验值动载荷的峰值误差在0.9%以内，证明仿真结果良好；速度是影响动载效应的重要因素，在速度提高至0.5m/s 后动载响应量平均增幅约1.2%；后轮的动载谷峰值在时间上对比前轮会有滞后，说明前后轮动载存在一定的相关性。

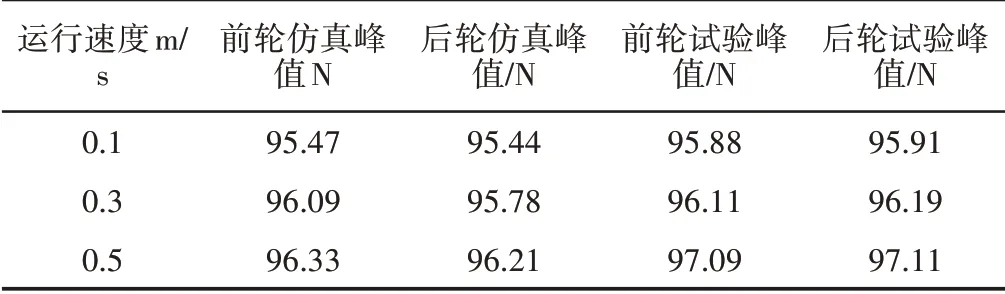
表3 动载峰值Tab.3 Peak Dynamic Load

对试验结果与数值解不同点分析，车辆实际行驶中的振动情况更加复杂，车辆自身的振动同样会影响动载荷的变化。

5 结论

这里建立了七自由度车−路耦合数学仿真模型，为进一步研究不同车轮的动载变化情况，构造了七自由度车−路耦合模型试验装置，验证了数学仿真模型的正确性。通过模型试验测试了车辆以不同速度行驶时对路面的动载荷，结合数值仿真解的对比分析，结论如下：

（1）通过试验证明了车辆后轮动载与前轮动载存在滞后性与相关性。试验平台结构合理，试验效果显著，可满足七自由度车−路间动载荷规律性测试。

（2）车速是影响车路耦合作用的重要因素，动载时域曲线波动幅值会随车速提升而大幅增加，进而对路面的破坏作用明显加强，通过规律性试验可对实际路面结构设计提供参考，为行车安全提供保障。

（3）发现车辆自身的振动同样会影响车辆动载荷，这包括车辆参数及车辆性能对动载荷影响。可以通过优化车辆参数，减缓车辆的振动，增加车辆的平顺性。

目前国内针对此类动载试验研究尚未有太多成果，这里装置设计是在实验室环境下对七自由度动载模型试验设备进行初步性探索，存在尚未解决的难题，将在今后的研究中进行完善。