“双减”背景下数学校本作业的精准实施

沈志勇|浙江省绍兴市柯桥区实验中学

编者按

自“双减”政策推行以来，各地教育部门深化教育改革，推出了一系列减负措施，而“双减”政策的落实很大程度上体现于作业改革的成效，因此教师对作业“减负提质”的实践和研究显得尤为重要。本期，我们以“‘双减’背景下的作业设计与实施”为主题，选登三篇来稿，以专题形式展示一线教师在新形势下对作业设计与实施的研究成果。

《关于进一步减轻义务教育阶段学生作业负担和校外培训负担的意见》要求“全面压减作业总量和时长，减轻学生过重作业负担”.那么，学校如何树立正确的作业观，完善作业研究、管理及支持体系，优化作业形式，提升作业质量呢？我校在集体备课、校本教研等团队建设机制下系统性地完善了作业管理制度，将作业分为校本作业、自主作业、实践作业三大类，其中校本作业为学生作业的主体.就数学学科而言，我校不购买任何教辅资料，数学教师基于数据实行数学校本作业的精准设计、精准辅导、精准反馈与干预，改聚焦“量”为关注“质”，以实现数学作业的减量提质.

一、作业数据的系统收集

教师系统收集学生学习全过程数据（如图1），操作步骤如下.

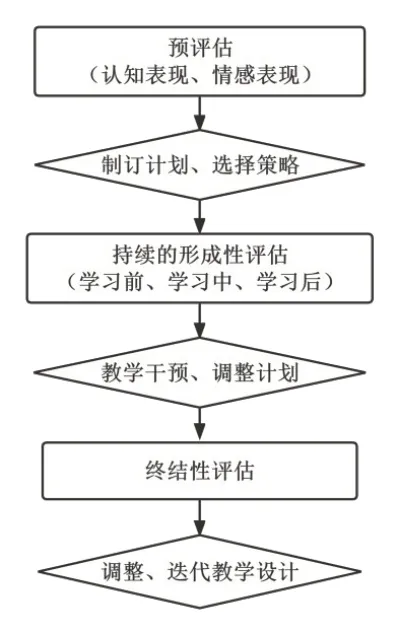
图1 系统性收集作业数据

第一步，教师对学生的认知表现、情感表现进行预评估：（1）布置学情检测作业，收集、分析数据，以确定教学中是否要补充相关基础知识、增加拓展内容，并选择合适的教学切入点；（2）了解学生的学习风格、兴趣与需要，选择最合适的教学策略.第二步，在教学的前、中、后期，教师开展持续性的形成性评估：（1）在学生学习跟不上、遇到挫折、浪费时间时，迅速进行干预；（2）发现学生有学习问题、出现学习差距时，及时采取应对措施，并调整接下来的学习任务和作业；（3）根据评估数据，为学生制订个性化的学习计划，以减少学生的厌倦和挫折感.第三步，教师将作业作为课时学习、单元学习的终结性评估：（1）根据作业数据，掌握学生个体的不足，设计个性化复习和练习作业；（2）掌握班级整体的不足，调整教学计划，迭代教学设计.下面是基于浙教版义务教育教科书《数学》（以下简称“浙教版教材”）八年级上册第2章《特殊三角形》的单元作业评估数据，迭代设计的案例.

【题目】长方形纸片ABCD（如图2）中，AB=4，BC=8，将它沿EF折叠，使C，A两点重合，点D落在点G处.请用2种方法证明△AEF是等腰三角形.

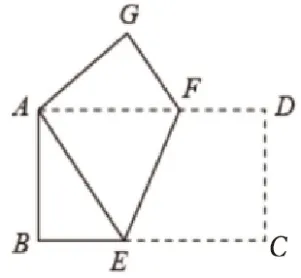
图2 长方形折叠

【数据】方法1：85%的学生通过证明△AFG≌△AEB，得到AE=AF.方法2：56%的学生分别在Rt△AFG、Rt△AEB中利用勾股定理建立方程，计算得到AF=AE=5.方法3：42%的学生采用折叠得到∠AEF=∠FEC，又因为长方形对边AD∥BC，所 以∠AFE=∠FEC，所 以∠AEF=∠AFE，所以AE=AF.方法4：6%的学生采用等积法证明；11%的学生只用1种方法证明.

【作业讲解设计迭代】笔者原计划培养学生的逻辑推理能力，重点讲解方法3.根据预评估数据，笔者改进设计，让不同层次的学生从不同的切入点和思考方向，展示其不同的解法.学生对比各种解题方法的优缺点，不断优化思维，丰富证明线段相等的方法.笔者指导学生寻找基本图形及基本图形之间的关系，从长方形对边、折叠的几何特性切入，关联平行线、角平分线的知识，逐步引导学生从几何直观解题进阶到逻辑推理解题；减少条件AB=4，BC=8，让学生探索结论是否成立，从而把握基本图形的本质；从折叠的几何特性切入，联结AC，让学生探索新的证明方法，为后续“证明四边形AECF为菱形”的教学作准备，加强几何教学的成长性、整体性.

二、系统实施流程下的作业精准设计

每份校本作业一般不超过12题，以简约、精准地为学生提供知识与技能结构化、系统化的支架，确保每个学生达成学习目标.校本作业分A、B、C三个层次，供学生选择，以满足不同的学生需要.

教师在系统的实施流程（如图3）下确保作业的精准设计.

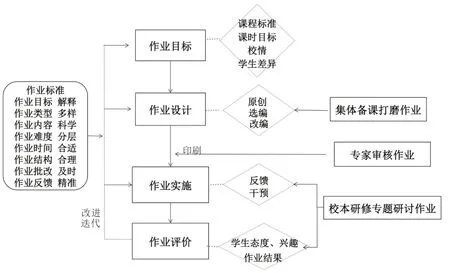
图3 作业的设计、实施流程

教师先解读课程标准、课时目标，结合校情、学生差异确定作业目标.接着，教师根据知识点、类型、表现水平三个维度分析学校作业大数据，确定A、B、C三个层次的候选作业.然后，教师根据作业标准，通过原创、选编、改编等方式设计作业初稿.在集体备课期间，教师们讨论作业目标的落实、打磨作业题、预设学生错误和干预方法、确定微课设计思路等，保证作业设计精准.最后，打磨稿由骨干教师、专家审核.

学生按学习基础和能力分别选做A，A、B，B、C层作业.教师要做的是：指导学生进行多种联系，促进知识与能力的结构化；指导学生运用多种方法策略，拓展创新思维能力；指导学生及时评价、复盘，提升质疑、反思能力.

三、基于微课平台的作业精准辅导

为实现作业的个性化辅导，教师每天给学生量身定制作业辅导微课.微课只点思路，只讲方法，不提供完整的解题过程和答案.每晚8时，我校微课平台自动推送，作业有困难的学生，哪里不懂点哪里.微课彻底实现了作业辅导的个性化，大大减轻了学生、教师和家长的负担.同时，学生在做作业、看视频、问问题、查学习进度的个性化学习的同时，又生成了个人、班级与整个年段的新一轮知识图谱.这既可为学生反思、制订适切的个性化复习方案提供数据依据，也可为教师的教学干预、复习决策提供重要的数据依据，从而确保每个学生的学习质量.

四、基于数据的作业精准反馈与干预

我校推行基于数据的“以学定教”课堂教学模式.教师应用“智学网”“十六进制”“教学助手”等平台布置学情检测作业.学生在课前明晰自己的学习情况，并在与同学的互动交流中，促进知识与技能的学习.教师课前批阅、分析，在掌握学情的基础上设计教学，对典型问题作深入研究与精准预设.如浙教版教材七年级下册第5章第2节《分式的基本性质》，是其所在章节教学的重难点.笔者分析数据，剖析学生的认知障碍，发现学生在这一知识点上的错误率超过35.2%，因此设计了让学生辨析的练习.师生充分交流讨论后，学生理解了分式的性质.这既可避免类似错误的重复出现，又渗透了分式性质学习的思维方式.

在不断的实践中，我校教师集体总结、提炼出了基于数据的校本作业分析、干预、改进模型，详见图4.

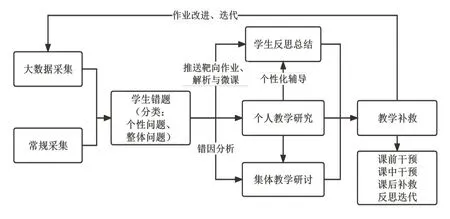
图4 基于数据的校本作业分析、干预、改进模型

通过对作业大数据、微课平台大数据的分析，教师对校本作业题的难易度、信效度进行评估，对学生的错因及时分析、干预，提炼课前干预、课中干预、课后补救的策略与机制.如：针对分散型错误，给学生提供归纳整理、自主反思支架；针对马虎型错误，给学生提供思辨、纠错支架；针对典型错题，组织学生开展“分析—模型—变式”专题学习.在此基础上，我校对下一年的校本作业作相应调整，以进一步提升作业的系统化、校本化.下面是基于数据的教师干预案例.

【题目】《九章算术》记载了一道有趣的数学题：“今有池方一丈，葭生其中央，出水一尺.引葭赴岸，适于岸齐，问水深、葭长各几何.”

【数据】45%学生观看辅导微课，其中30%的学生不能构造直角三角形，标注数据.

【访谈】学生不能把条件“池的正中央”表达成数学语言，10%的学生未掌握构造直角三角形解决问题的方法，10%的学生不能用未知数表示水深、葭长.

【干预】交流讨论，提炼解决实际问题的步骤.（1）画图：长方体（图形语言，以下图均略）.（2）构造：求AB，必须要构造以AB为一边的三角形（化归思想）.（3）连线：作BC⊥AD于点C，得Rt△ABC（数学语言）.（4）表示：“池的正中央”BC=5，葭长AB=x（数学语言）.

【改进】创设吸引学生的问题情境.□◢