圆柱螺旋弹簧轻量化设计探讨
熊志远,宋瑞祥,赵 娜,赵 阳
(北京市劳动保护科学研究所,北京100054)
1 引言
弹簧按形状可分为碟形弹簧、环形弹簧、扭杆弹簧以及圆柱螺旋弹簧等,其中圆柱螺旋弹簧是应用最为广泛的一类弹簧。圆柱螺旋弹簧可用于缓冲减振,例如:安装在车身和车轮之间的悬架螺旋弹簧;安装在水泵、风机等动力设备与基础之间的隔振弹簧。它还可用于控制机械运动,如内燃机中的阀门弹簧、离合器中的控制弹簧以及凸轮机构的压紧弹簧。圆柱螺旋弹簧也可用于测量力的大小,如弹簧秤或弹簧测力计中的弹簧。
圆柱螺旋弹簧是汽车悬架的重要组成部分,其轻量化能促进汽车整备质量的降低,有利于提高汽车动力性能、减少燃料消耗、降低排气污染。轻量化的隔振弹簧,能够给装卸、运输等带来便利。便携式弹簧秤轻量化后,更便于人们轻松携带。
文献[1]基于基因遗传算法,对一内燃机用气门圆柱螺旋弹簧进行模糊优化设计,结果弹簧减重29.7%。文献[2]应用混合遗传模拟退火算法对某采油树阀门执行机构内部一圆柱螺旋弹簧进行优化设计,优化结果与传统设计法相比,弹簧减重17.50%。文献[3]运用Matlab对管道机器人中的圆柱螺旋弹簧进行了优化设计,结果弹簧减重10%。文献[4]分别运用传统弹簧设计方法和Matlab方法对某电子设备使用的圆柱螺旋弹簧进行设计计算和优化,结果表明:传统方法及Matlab方法所设计的弹簧体积分别为22.8mm3与16.6mm3。
对圆柱螺旋弹簧进行轻量化设计除了上述结构优化外,还有运用新材料。文献[5]将树脂传递模塑技术和纺织技术相结合制备出复合材料圆柱螺旋弹簧,并导出了弹性常数。文献[6]利用玻璃纤维与环氧树脂制备了复合材料圆柱螺旋弹簧,探讨了弹簧的加工工艺及结构参数对其弯曲回弹力、回复率和拉伸性能等的影响。文献[7]研究了任意形状的复合材料螺旋弹簧的动态行为。文献[8-9]分别基于多目标优化设计软件,对复合材料螺旋弹簧的最小质量与最大刚度进行了优化设计。文献[10-11]对碳纤维复合材料圆柱螺旋弹簧的刚、强度性能进行了理论预测与仿真研究。文献[12]对车用复合材料螺旋弹簧进行了优化设计,优化后的复合材料弹簧比金属弹簧质量减轻了34.4%。
圆柱螺旋弹簧轻量化设计不同于现有的结构优化,它探讨了空心簧丝圆柱螺旋弹簧的刚、强度性能与重量之间的变化关系,探究一种新的圆柱螺旋弹簧轻量化设计方法,以期给已有的各种设计方法提供补充参考。
2 空心簧丝圆柱螺旋弹簧的刚强度
空心簧丝圆柱螺旋弹簧在P力作用下进行压缩的示意图,如图1所示。与该弹簧对应的相关参数,如表1所示。空心簧丝的内、外径分别用di、d o表示,下标“i”与“o”分别为英文“inside”与“outside”的第一个字母。实心簧丝圆柱螺旋弹簧受到一定压力时的最大剪应力及刚度均有经典的理论分析[13],将对空心簧丝圆柱螺旋弹簧受压时的最大剪应力及刚度进行理论推导。
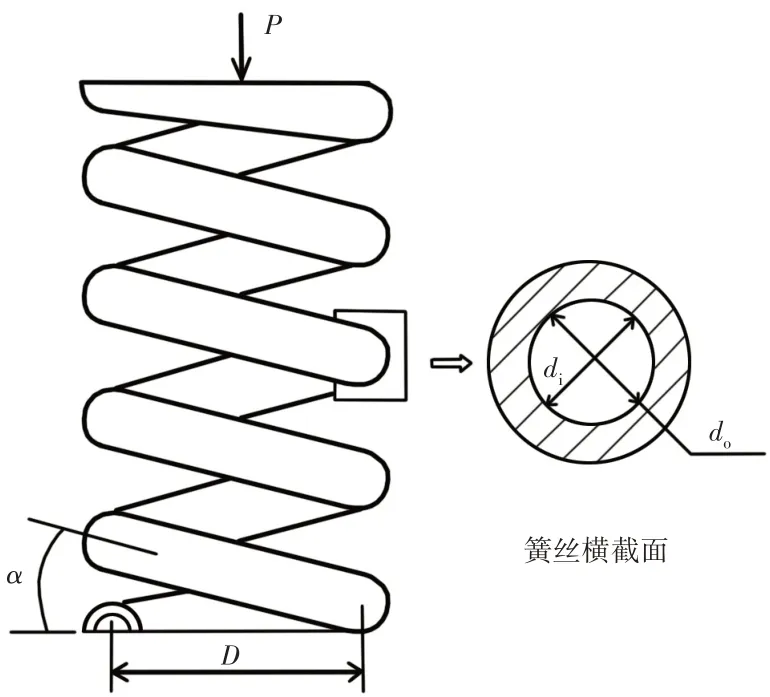
图1 空心簧丝弹簧示意图Fig.1 Diagram of Spring with Hollow Spring Wire
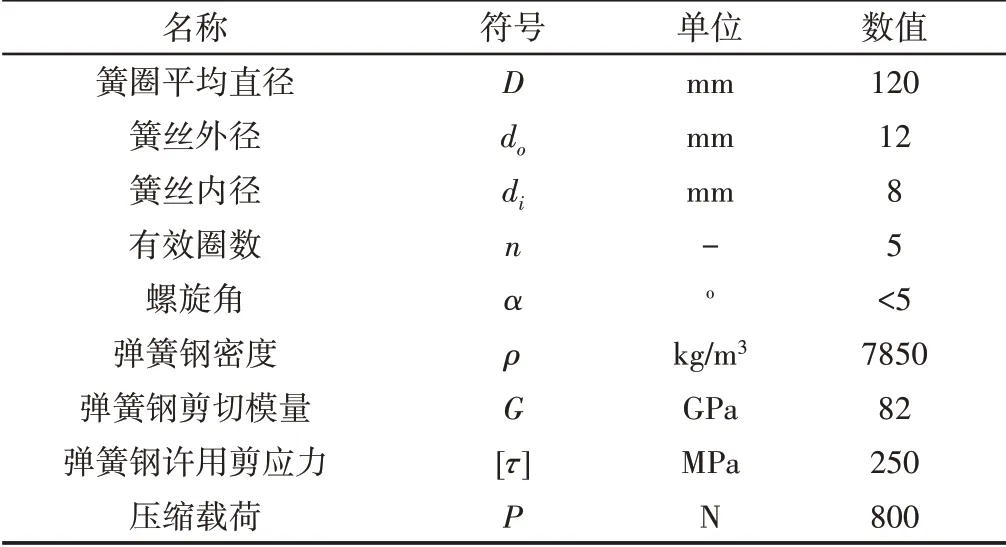
表1 空心簧丝弹簧的相关参数Tab.1 Relevant Parameters of Spring with Hollow Spring Wire
当α<5º时,便可忽略α的影响,近似认为簧丝横截面与弹簧轴线在同一平面内,据此截取弹簧上部分,如图2所示。为保持该部分平衡,簧丝横截面上应有一个剪力Q和一个力偶矩T,且Q=P,T=P D∕2。
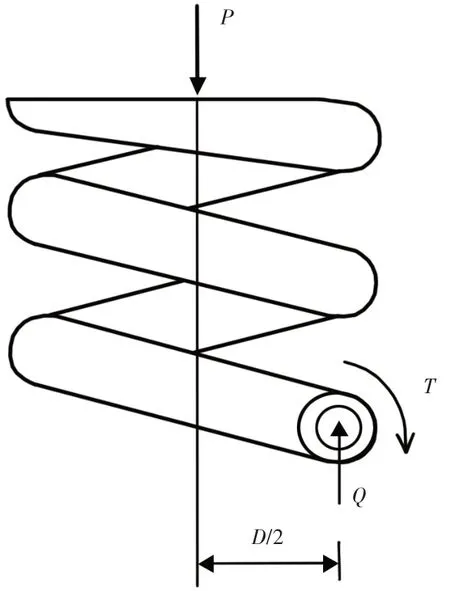
图2 基于簧丝任意横截面截取的弹簧上部分Fig.2 Based on the Arbitrary Cross Section of Spring Wire the Upper Part of the Spring to be Cut Out
与Q对应的剪应力τ1,认为在簧丝横截面上均匀分布,如图3(a),其表达式为:

表1中,簧丝外径do与簧圈平均直径D之比为0.1,故可略去簧丝曲率的影响,近似用受扭的空心直杆公式表示τ2,其表达式为[13]

式中:r—簧丝横截面上应力所在点到圆心的距离,如图3(b)所示。
图3中,最大合应力位于簧丝截面最左边缘处,将r=do∕2代入式(2)后,并与式(1)相加,可得
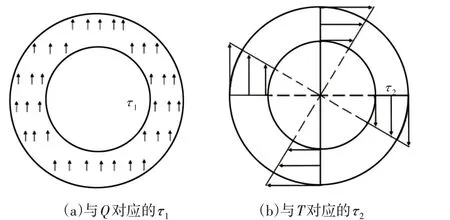
图3 横截面上的剪应力Fig.3 Shear Stress on Cross Section
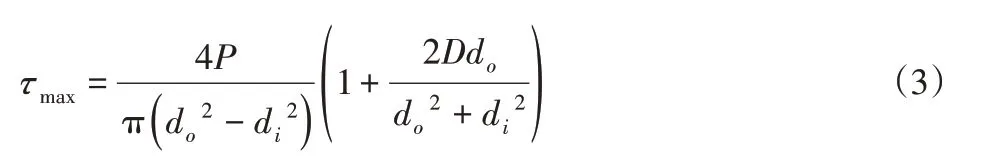
右边括号内的1与剪力Q对应与纯扭对应。将表1中的相关数据代入,计算结果为13.85,1与之相比可省略,式(3)简化为:

载荷P对弹簧所做的功W为:

基于式(2)和图3(b)作图,如图4所示。图4是横截面上距圆心为r的点处的剪应力τ2。单位体积变形能u可表示为:

图4 距圆心为r的点处的剪应力τ2Fig.4 Shear Stressτ2 at the Point That is r Away From the Center of the Circle

整个弹簧储存的变形能U为:
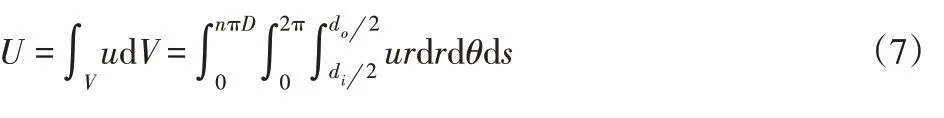
式中:rdrdθ—截面上的微分面积;ds—沿簧丝轴线的微分长度。
将式(2)代入式(6),再将式(6)代入式(7),计算结果为:

载荷P对弹簧所做的功W应等于弹簧所储存的变形能U,由式(5)等于式(8),可得弹簧刚度表达式为:

3 圆柱螺旋弹簧性能与重量变化关系
3.1 刚度性能与重量变化关系
3.1.1 仅簧丝内径di变化时的情况
将表1中的相关数据代入式(9),其中只允许簧丝内径di变化,作出弹簧刚度K与簧丝内径di的关系曲线,如图5所示。
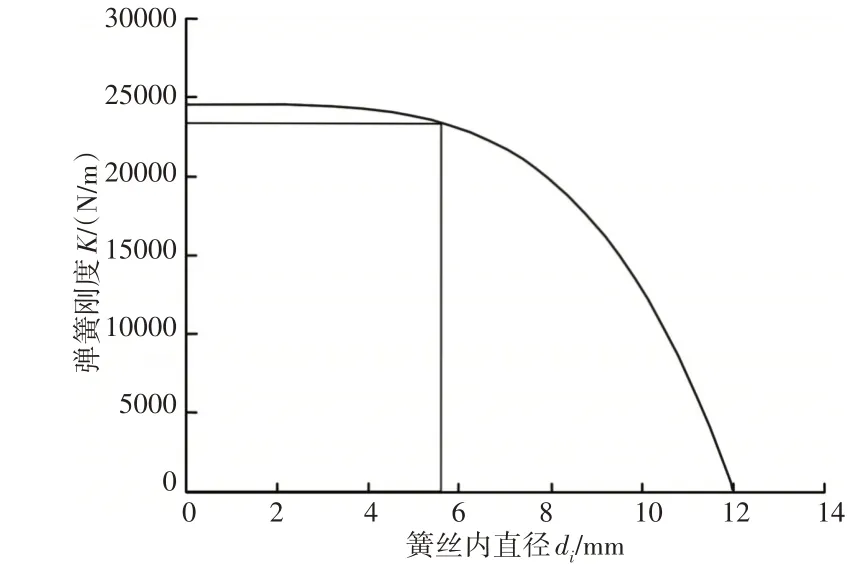
图5 弹簧刚度K与簧丝内径di的变化关系Fig.5 Relationship Between the Stiffness of Spring K and the Inside Diameter of Spring Wire di
关系曲线表明:随着簧丝内径增加,弹簧刚度下降,即:在簧丝外径(12mm)等其他参数不变的情况下,随着空心簧丝壁厚越来越薄,弹簧的刚度也是越来越低的,但是在曲线的不同区域,弹簧刚度的降低程度是不一样的。将簧丝内径di=0mm及表1中的其他相关参数代入式(9),可得实心簧丝弹簧的刚度为24600N∕m,与图5中曲线与纵轴的交点位置相符。设定弹簧刚度下降率为5%,对应的空心簧丝弹簧的刚度为23370N∕m。将表1中的相关数据代入式(9),并令其等于23370N∕m,可计算出簧丝内径di=5.67mm,见图5中直线。将该位置点定为减重设计最佳点,即认为该点是刚度下降尽量小、重量下降尽量多的平衡点。
空心簧丝圆柱螺旋弹簧的重量计算式为:

式中:g—重力加速度,取9.8m∕s2。将do=12mm、di=0mm及表1中相关数据代入式(10)后,计算得实心簧丝弹簧重为16.38N。同样,将do=12mm、di=5.67mm及表1中相关数据代入式(10)后,计算得空心簧丝弹簧重为12.73N。空心簧丝相比于实心簧丝弹簧,重量下降22.28%。可见,刚度损失5%,减重却可达22.28%。
3.1.2 仅簧丝外径do变化时的情况
模拟法人实体运行机制是指以效益为中心,以成本为主线,将市场机制引入企业内部,实现实业部、工序等主体的独立核算、自主经营、自负盈亏。接受营业收入、利润、成本、资金占用等指标,以及安全、质量、环保等指标的考核,经营成果与工资总额挂钩,做到绩效与监督同步、激励与制约并重。以建立压力层层传递、指标层层分解、责任层层落实、绩效层层考核、活力层层激发的新机制,充分调动企业内部方方面面的积极性、主动性和创造性。
将表1中的相关数据代入式(9),其中只允许簧丝外径do变化,作出弹簧刚度K与簧丝外径do的关系曲线,如图6所示。关系曲线稍微向右下方凸出,而且随着簧丝外径do的增加,弹簧刚度K的增加量愈来愈显著。
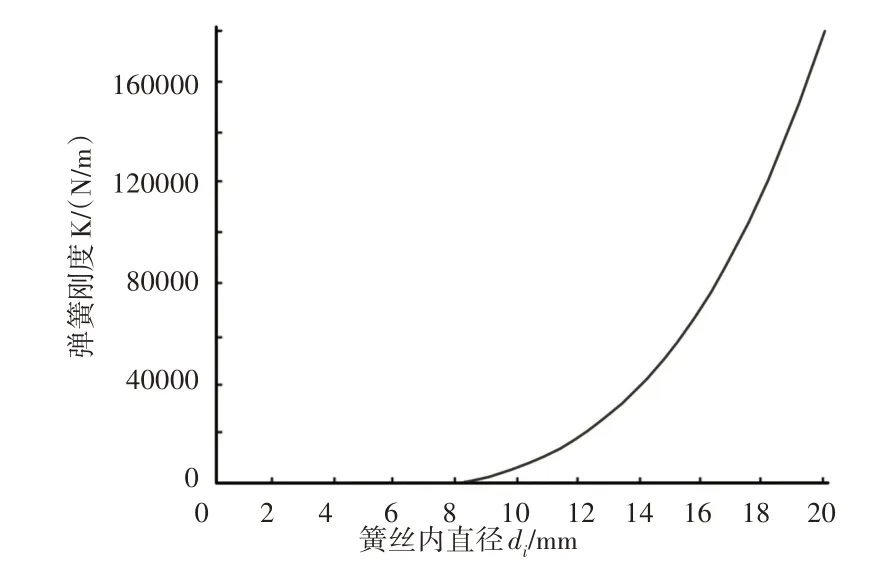
图6 弹簧刚度K与簧丝外径do的变化关系Fig.6 Relationship Between the Stiffness of Spring K and the Outside Diameter of Spring Wire do
3.1.3 簧丝内、外径d i、d o同时变化的情况
将表1中的相关数据代入式(9),其中允许簧丝内、外径d i、do变化,作出弹簧刚度K与簧丝内、外径d i、do的关系曲面,如图7所示。图7中的上、下两图是针对同一曲面的不同角度投影。
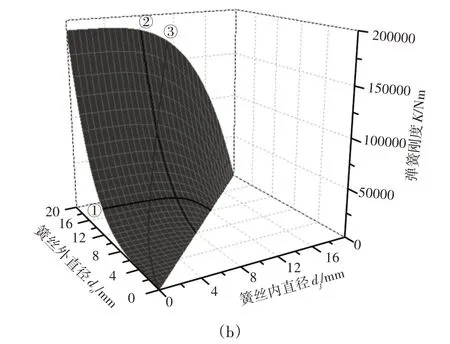
图7 弹簧刚度K与簧丝内、外径d i、do的变化关系Fig.7 Relationships Between the Stiffness of Spring K and the Inside,Outside Diameters of Spring Wire d i,do
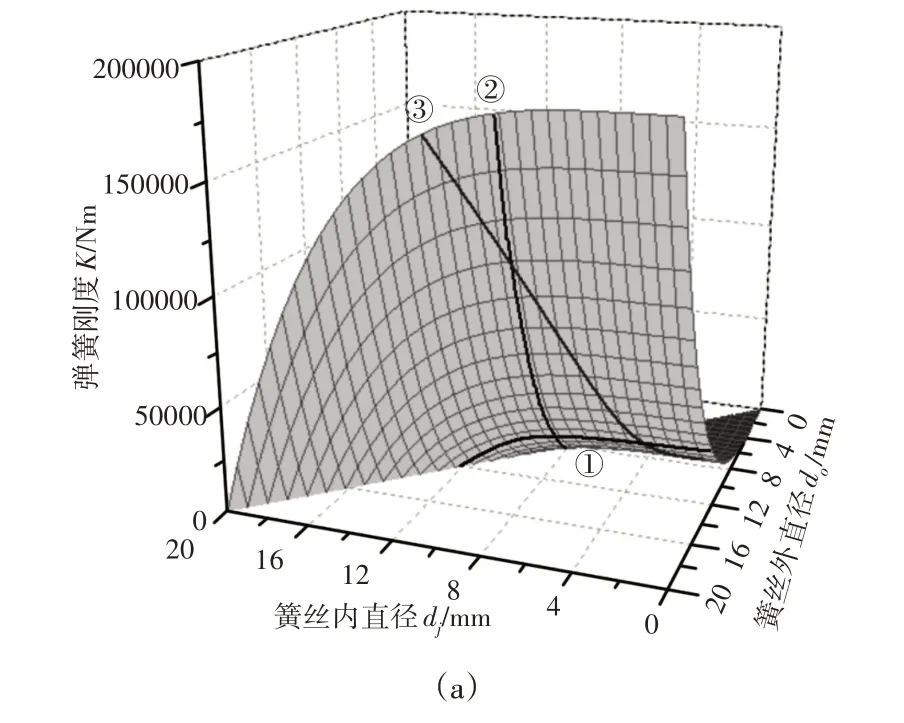
图7中,底面上两垂直坐标分别代表弹簧空心簧丝的内径di和外径do,纵坐标表示弹簧刚度。在正方形底面上,对角线do=di上的点代表空心簧丝的内、外径相等,该处弹簧不存在,刚度为零;在do
从图7中可以看到,假定簧丝的外径do取定某一个具体的值时,弹簧刚度K随内径di的增加,首先经历一个平缓下降区域,然后急剧下降。图中①号曲线就是外径do=12mm的平面与曲面相交的交线,即图5所示的曲线。假定簧丝内径d i取定某一个具体值时,弹簧的刚度K将随簧丝外径do的增加而急剧增加。图中②号曲线就是内径d i=8mm的平面与曲面相交的交线,即图6所示的曲线。
当簧丝外径分别为4mm、8mm、16mm、20mm时,同样可计算得相应的簧丝内径与弹簧刚度,如表2所示。从而可在图7中的曲面上得到曲线③。通过曲面上标注的③号曲线,设计时既能够通过增大或缩小簧丝外径来快速提高或降低弹簧的刚度,又能够通过选取适当的内径来实现产品减重的目的。
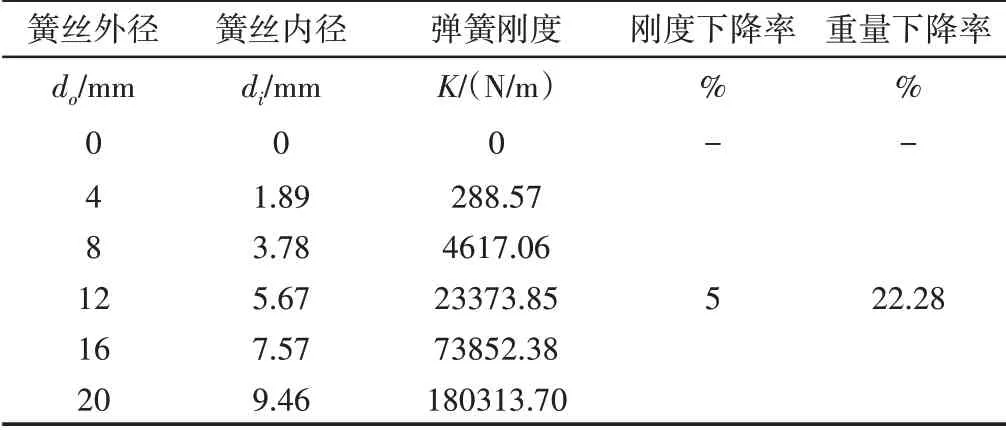
表2 刚度下降5%时对应的设计参数Tab.2 Corresponding Design Parameters When Stiffness Decreases by 5%
3.2 强度性能与重量变化关系
同一载荷作用下,构件最大应力越大,强度越低;反之,强度越高。
3.2.1 仅簧丝内径di变化时的情况
将表1中相关数据代入式(4),其中只允许簧丝内径di变化,作出最大剪应力τmax与簧丝内径di的关系曲线,如图8所示。
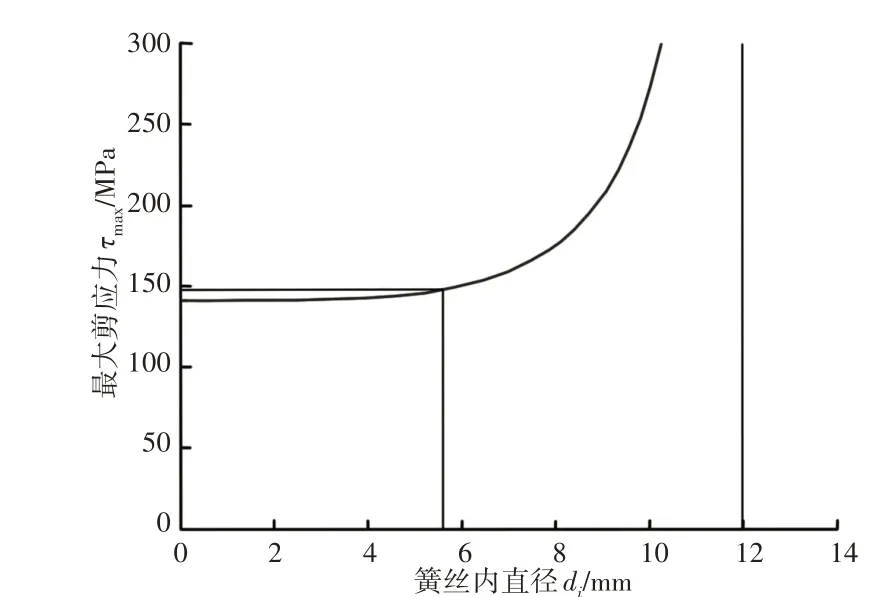
图8 弹簧最大剪应力τmax与簧丝内径di的变化关系Fig.8 Relationship Between the Maximum Shear Stress of Springτmax and the Inside Diameter of Spring Wire di
关系曲线表明:随着簧丝内径的增加,最大剪应力τmax也增加,但在曲线不同区域,最大剪应力τmax增加程度不同。将di=0及表1中的相关参数代入式(4),计算得实心簧丝弹簧最大剪应力为141.54MPa,与图8中曲线与纵轴的交点位置相符,若该最大剪应力τmax增加5%,即为148.62MPa。将表1中的相关数据代入式(4),并令其等于148.62 MPa,计算出空心簧丝内径di=5.61mm,见图8中直线。这里将该点定为减重设计最佳点,即认为该点是强度下降尽量小、重量下降尽量多的平衡点。
将do=12mm、di=5.61mm以及表1中相关数据代入式(10),经计算得空心簧丝弹簧重为12.80N;又已知do=12mm的实心簧丝弹簧重为16.38N,则空心簧丝相对于实心簧丝弹簧减重率为21.86%。可见以较小的强度损失可以获得较多减重。
3.2.2 仅簧丝外径d o变化时的情况
将表1中的相关数据代入式(4),其中只允许簧丝外径do变化,作出最大剪应力τmax与簧丝外径do的关系曲线,如图9所示。很明显,最大剪应力τmax与簧丝外径do的变化关系是一条曲线,随着簧丝外径do的增加,最大剪应力τmax急剧下降,即强度显著增强。
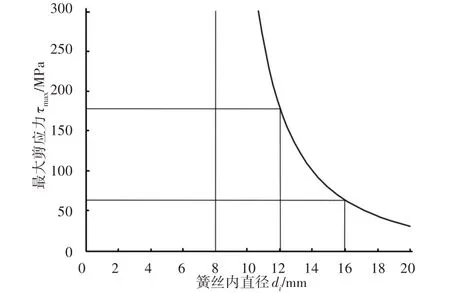
图9 弹簧最大剪应力τmax与簧丝外径do的变化关系Fig.9 Relationship Between the Maximum Shear Stress of Springτmax and the Outside Diameter of Spring Wire do
3.2.3 簧丝内、外径di、do同时变化的情况
将表1中相关数据代入式(4),其中允许簧丝内、外径di、do同时发生变化,作出最大剪应力τmax与簧丝内、外径di、do的关系曲面,如图10所示。图10中的上、下两图是针对同一曲面的两个不同角度的投影。在正方形底面的对角线d o=di上,式(4)分母为0,最大剪应力τmax理论上为无穷大;在do
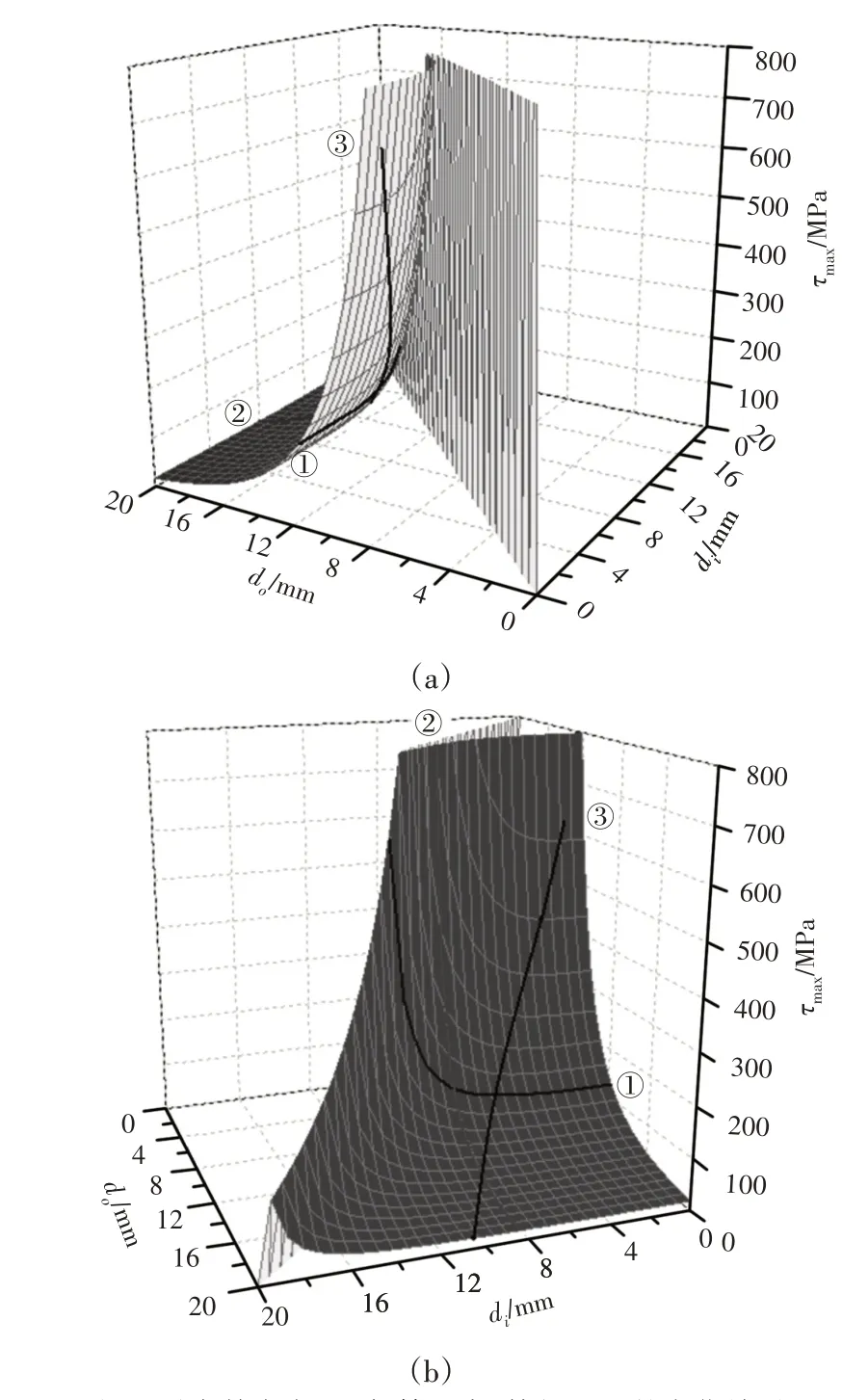
图10 最大剪应力τmax与簧丝内、外径di、do的变化关系Fig.10 Relationships Between the Maximum Shear Stressτmax and the Inside,Outside Diameters of Spring Wire di,d o
从图10中可以看到,假定簧丝的外径do取定某一个具体的值时,最大剪应力τmax随内径di的增加,首先经历一个平缓上升区域,然后急剧上升。图中①号曲线就是外径d o=12mm的平面与曲面相交的交线曲线,如图8所示。假定簧丝的内径di取定某一个具体值时,最大剪应力τmax将随簧丝外径do的增加而急剧下降。图中②号曲线就是内径di=8mm的平面与曲面相交的交线,如图9所示。
当簧丝外径分别为4mm、8mm、16mm、20mm时,同样可计算得相应的簧丝内径与弹簧最大剪应力如表3所示,从而可在图10中的曲面上得到曲线③。通过曲面上标注的③号曲线,设计时既能通过增大或缩小簧丝外径来快速提高或降低弹簧强度,又能够通过选取合适的内径来实现产品减重的目的。
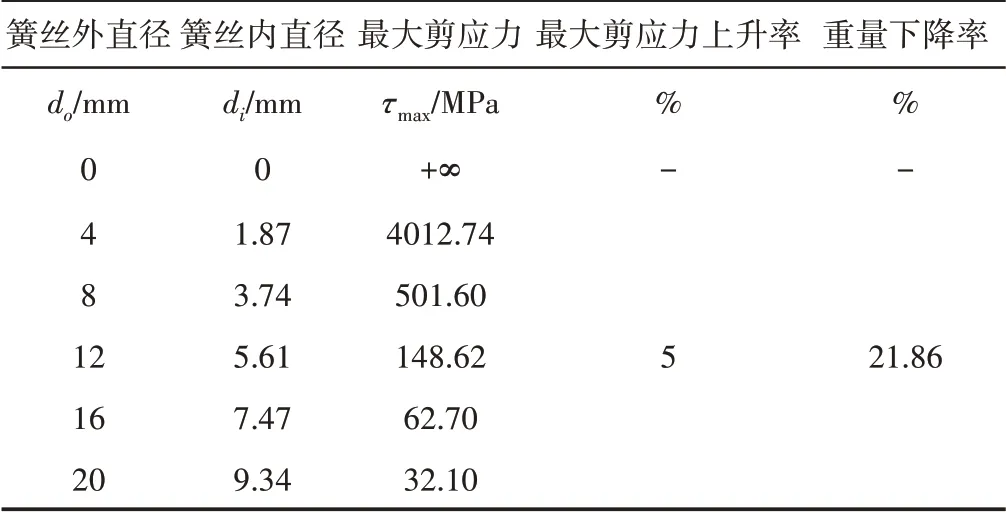
表3 强度下降5%时对应的设计参数Tab.3 Corresponding Design Parameters When Strength Decreases by 5%
4 结论
首先,理论推导了空心簧丝圆柱螺旋弹簧受压时的最大剪应力、刚度;然后,基于最大剪应力、刚度及提供的弹簧实例数据,探讨了空心簧丝弹簧的刚、强度性能与重量之间的变化关系,得到如下结论:
(1)随着簧丝内径的增加,弹簧刚度逐渐降低;当弹簧刚度下降5%时,弹簧减重22.28%;该位置点被认为是刚度下降尽量小、重量下降尽量多的最佳设计点。
(2)随着簧丝内径的增加,弹簧强度逐渐降低;当弹簧强度下降5%时,弹簧减重21.86%;该位置点被认为是强度下降尽量小、重量下降尽量多的最佳设计点。

