下肢康复训练机器人膝踝协调运动控制方法

邢艳丽，亢 瑾

（1.衡水学院，河北 衡水 053000；2.华北理工大学，河北 唐山 063210）

1 引言

在医疗保健水平不断提高背景下，下肢康复训练机器人逐渐进入人们视野，下肢康复训练机器人属于医疗机械范畴，能够协助运动功能受损患者进行康复训练，在大脑皮层中重塑运动神经记忆，使患者渐渐恢复运动能力。其涉及传感器、计算机、人工智能等多种技术，因此它在恢复下肢运动功能方面发挥出化学药物无法替代的作用。但是，传统的康复机器人操作较为复杂，患者通常是较为被动地跟随系统做训练，不能根据人体自然状态进行协调运动，所以在临床推广中受到一定阻碍。为此，相关学者提出如下方法。

文献[1]提出康复机器人个性化步态规划方案。根据旋量理论构建运动模型，对机器人关节运动路径进行统一规划，调整轨迹与运动速度，通过对步态参数的实时采集和轨迹跟踪，该方法确保步态调整规划符合人体行走的生理特征。文献[2]研究一种通过上肢控制对侧受损下肢的康复训练方式。利用系统测量正常行走时上肢的肩部、肘关节转角以及下肢的髋、膝关节转角，得到人体上、下肢步态运动路径，并对其做包络分析获得参考曲线，使用模糊理论建立上肢与下肢运动之间的主从映射关系，得出下肢运动的输出值。但是上述控制方法只是考虑了下肢肌群意识，并未考虑下肢康复训练机器人的不确定性，无法最大程度实现协调运动。

基于此，提出一种自适应迭代控制的下肢康复训练机器人膝踝协调运动控制算法。迭代学习控制具有人工智能与自动控制的综合优势，经过不断重复控制，修正控制律。将自适应控制方法与其相结合，能够获取大量和模型相关的经验信息，克服迭代算法局限性，适用于具有重复运动性质的被控目标。此研究的提出为下肢残疾人士提供性能优良的产品，同时促进理疗福利事业的发展。

2 膝踝关节运动学分析

2.1 标识点数量与位置设置

为了准确计算下肢康复训练机器人步态特征参数，设置标识点数量与位置对计算结果精度起到很大影响。在设置标识点时，必须遵循下述四项原则：（1）标识点需面对传感器，不要出现遮挡现象；（2）所选标识点需覆盖全部待测试的下肢骨骼与关节；（3）标识点运动需要和骨骼、关节的运动相一致；（4）要满足数据处理与步态特征参数计算[3]。

按照以上原则，在被测下肢康复训练机器人设置五个标识点，分别在髋关节、膝关节、踝关节的外侧转动中心各选一个，此外在足背前侧与后端分别设置一个。在行走过程中，A、B、C、D、E五个点随人体下肢一起运动，其位移状况会被传感器记录，获取下肢骨骼与不同关节的运动信息[4]。构建完全体现下肢刚体模型运动的局部坐标系，如图1所示。

图1 下肢刚体模型运动局部坐标系Fig.1 Moving Local Coordinate System of LowerLimb Rigid Body Model

令坐标系的XOY平面位于矢状面，且Y轴正方向竖直向上。这时下肢模型中连杆在矢状面的运动状况只和X、Y坐标有关。其中，A、B、C三个点能够体现髋、膝、踝三个关节的运动轨迹，A、B两点的连线在矢状面的投影和大腿连杆中心线相吻合，表示大腿，B、C两点的连线代表小腿；C、D、E三点组成的三角形为足，线段和足底相互平行。

2.2 步态特征参数计算

设置标识点数量与位置后，利用运动捕捉系统对标识点的空间坐标进行测试，获取步态特征参数。假设单侧下肢刚体模型中五个标识点在坐标系中的坐标分别为A（xa，ya，za）、B（xb，yb，zb）、C（xc，yc，zc）、D（xd，yd，zd）、E（xe，ye，ze），相邻标识点的长度分别表示为lab、lbc、lcd、le d以及le c，髋关节、膝关节与踝关节角描述为θhip、θknee与θankle，的垂线和之间的夹角记做θf，与之间的夹角是θn，因此A、B、C、D四个标识点在矢状面的运动学方程表示为：

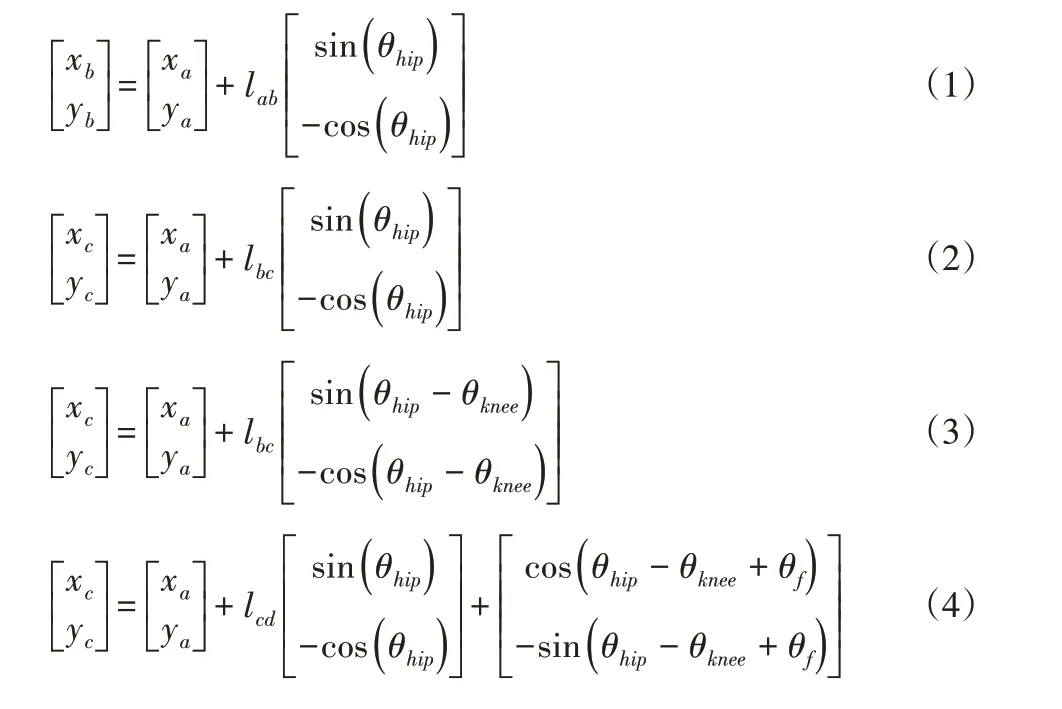
由于θn是C、D、E三个标识点组成的三角形内角，且均粘贴在足的外侧，所以这些点之间的相对位置不会发生改变[5]，则θn的计算公式为：

结合θankle和θf角度正方向定义，明确两者之间需要符合下述关系：

因此相邻标识点的连接线长度lab、lbc、lcd、led、le c的表达式为：

通过上述公式做运动学反解，获得θhip、θknee与θankle三个关节的数学表达式：

在获取θhip、θknee与θankle值后，根据相邻标识点之间的长度，结合获得所需的步态特征参数。

2.3 膝踝关节转角数学建模

利用步态特征参数，分别构建膝关节与踝关节的转角数学模型。膝关节转角变化趋势由两个波峰构成，且波峰的峰值相距较远，每个波峰的中心均不完全对称[6]。由此可以得出一个步态周期膝关节转角变化轨迹和高斯函数曲线的波分特征较为相近，可通过高斯函数，实现膝关节转角数据拟合。但是由于高斯函数基本形式为单峰曲线，无法同时对不对称的波峰曲线进行拟合，因此建立一种高斯函数扩展形式，来拟合此种非中心对称的双峰曲线，函数表达式如下：

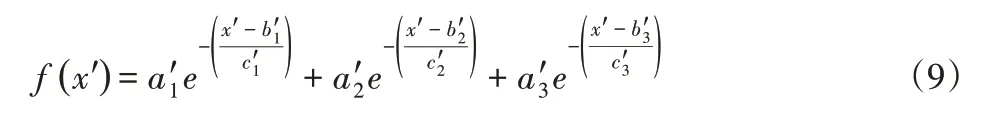
式中：x'—函数自变量；a'、b'、c'—常数系数。

将膝关节转角非中心对称的双峰曲线函数表达式作为基础，构建膝关节转角数据的数学模型为：

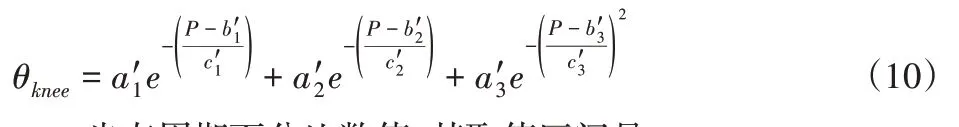
式中：P—步态周期百分比数值，其取值区间是[0，100]。

（2）踝关节转角模型

踝关节与膝关节的转角有所不同，当使用单一函数对其进行拟合时，获得的拟合曲线会有偏差[7]。为确保模型精度，利用分段曲线拟合形式对踝关节转角参数进行拟合。根据自变量取值区间的差异进行分段表示，获得一个较为完整的拟合结果。假设，存在实数a'，b'1，b'2，…，b'i-1，c'，且符合，若函数f（x'）在区间［a'，c'］上存在定义，则踝关节转角模型表示为：

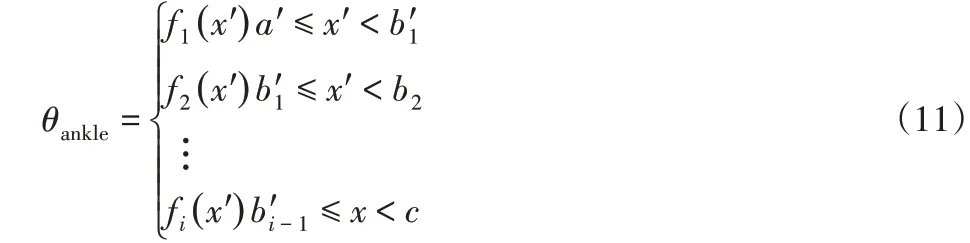
3 基于自适应迭代学习的膝踝协调运动控制

3.1 迭代学习控制

根据膝踝关节运动学特征，利用自适应迭代控制算法实现膝踝协调运动。在该算法中，一般情况下将膝踝关节运动特性变换为以下形式：

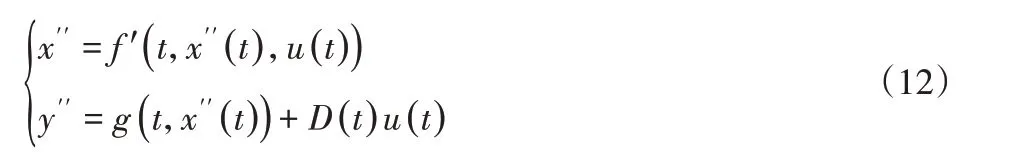
式中：x''∈Rn；u∈Rr；y''∈Rm；f'、g—对应维数的矢量函数。根据迭代控制理论能够描述为：针对一个被控系统，已知期望输出值为，存在与其相对的期望输入ud（t）以及每次运动的原始状态，需经过多次反复运行（K→∞），获得用于修正控制的学习率[8]，确保系统控制输入在时间t∈［0，T］内收敛，使系统输出为在迭代学习控制过程中需先假设符合以下条件：

期望轨迹是设定好的并且已知；相邻两次计算时间需固定；原始状态始终保持不变；只能具有一个控制输入u（d t）；每次的计算输出结果都能够被测出。

基于上述假设，迭代控制算法构建了一系列迭代控制序列信号［9］｛uk｝，它和任意一个能够实现的控制信号u*（t）之间存在较小误差，且u*（t）属于下述公式的最佳解：

结合假设条件，对膝踝运动轨迹进行第k次跟踪时，公式（13）变换为下述形式：

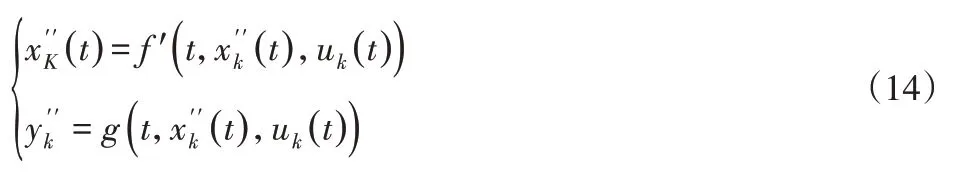
则输出误差表示为：

合理利用输入误差e'k(t)与控制输入uk（t），得出下次跟踪时的控制输入：

确保当k→∞时在t∈［0，T］区间内：

3.2 自适应迭代学习控制方法

但是上述方法只能通过提高学习速率来减少迭代次数，收敛性能较差。为此，将自适应算法引入到迭代控制中，自适应修正训练机器人运动控制期望轨迹，解决运动控制连续步态协调问题，从而提高控制性能，确保膝踝协调运动。

由膝踝动力学方程可知，膝踝协调运动就是在有限时间间隔［0，T］内能够反复进行正常平地的行走任务，利用公式表示为：

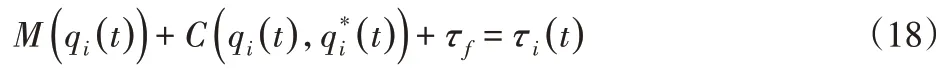
式中：σ—正规矩阵。

4 实验数据分析与研究

为了验证下肢康复训练机器人膝踝协调运动控制方法的有效性，实验利用北方数码公司（Northern Digital Inc.Canada，NDI）的Optotrak Certus主动式光学运动捕捉系统对标识点的空间坐标进行测试。下肢康复训练机器人采用三段式腿结构，髋关节、膝关节和踝关节均为串联弹性驱动关节，下肢康复训练机器人结构，如图2所示。

图2 下肢康复训练机器人结构Fig.2 Robot Structure of Lower Limb Rehabilitation Training

下肢康复训练机器人物理参数，如表1所示。

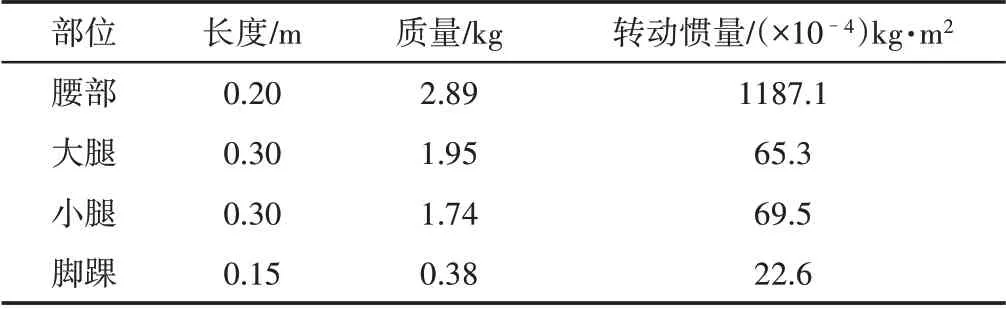
表1 下肢康复训练机器人物理参数Tab.1 Physical Parameters of Rehabilitation Training Robot

此次实验，主要分析膝踝协调运动的控制效果，分别采用文献[1-2]和这里方法，对比经过不同迭代次数后，不同方法的膝踝协调运动控制效果和膝踝协调运动速度误差结果，如图3、图4所示。

由图3和图4可知，这里方法的膝踝协调运动连续步态较为协调，膝踝协调运动控制效果较好，显示出较好的速度控制效果，能够在较短时间内，使速度误差控制在要求范围内。这是因为这里对迭代控制算法进行一定改进，通过自适应控制策略获得大量相关经验信息，提高控制性能，确保膝踝协调运动。

图3 不同方法的膝踝协调运动控制效果Fig.3 Effect of Knee-Ankle Coordination Motion Control by Different Methods

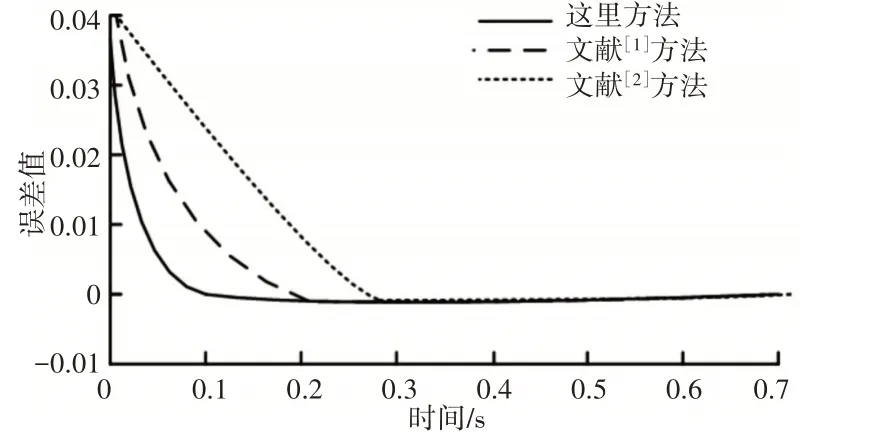
图4 不同方法的膝踝协调运动速度误差Fig.4 Velocity Error of Knee Ankle Coordinated Motion with Different Methods

在此基础上，进一步对迭代控制位置误差进行测试。这里方法在经过3次迭代后，膝关节与踝关节的迭代控制位置误差，如图5、图6所示。

图5 膝关节迭代控制位置误差Fig.5 Iterative Control Position Error of Knee Joint

图6 踝关节迭代控制位置误差Fig.6 Position Error of Ankle Joint Iterative Control

由图5和图6能够看出，膝关节与踝关节均经历三次迭代后控制误差值达到最小。表明本文控制方法的收敛速度较快，经过较少次数的迭代便可以满足误差需求，同时，膝踝两关节迭代次数相同，表明协调运动效果较好。

5 结论

针对下肢康复训练机器人膝踝协调运动控制方法，本文提出一种自适应迭代学习控制策略，改进了传统迭代算法的不足，减少控制误差，实现膝踝协调运动，研究结果如下：

（1）这里的方法的膝踝协调运动步态连续，膝踝协调运动速度误差较小，能够在较短时间内，使速度误差控制在要求范围内。

（2）这里的方法经过较少次数的迭代，膝关节和踝关节迭代控制位置误差达到最小，收敛速度较快，膝踝协调运动控制效果较好。