椭圆式异形压缩螺旋弹簧力学特性计算分析

李颂，周长城，张云山，李鹏雷

(1.山东理工大学 交通与车辆工程学院，山东 淄博 255049；2.山东汽车弹簧厂淄博有限公司，山东 淄博 255410)

螺旋弹簧是最基本的弹性元件之一，广泛应用于汽车等工业中[1],其中最为常见是圆柱螺旋弹簧[2]。这类弹簧安装时，对空间有一定的要求，但在某些特殊的应用中，空间受到限制，使用组合圆柱螺旋弹簧又无法满足刚度要求[3-4]，此时椭圆式螺旋弹簧可以很好地解决这个问题。

目前，螺旋弹簧设计的相关标准多适应于圆形中径螺旋弹簧[5]，国内外学者的研究也多以圆柱螺旋弹簧为基础进行。Wahl[6]将螺旋弹簧看作受剪切和扭转作用的圆杆，分析得出了圆柱螺旋弹簧的刚度公式。张健等[7]以改进后的精确几何模型梁单元为基础，对圆柱螺旋弹簧的非线性特性进行了分析。然而目前对于椭圆形中径螺旋弹簧的研究却非常少。张英会[8]给出了椭圆形弹簧圈螺旋弹簧的变形及应力的计算式，但是此计算式是将椭圆形中径等效成圆形中径弹簧得出的近似修正式。对于椭圆形丝径的研究，日本弹簧协会以等圆面积法对椭圆形截面簧进行了计算分析[9]。Gzal等[10]给出了小螺旋角椭圆截面簧的应力公式，但其仅考虑扭转应力作用，也忽略了曲率的影响。上述文献所用的研究分析方法虽然准确，但只考虑了弹簧圈为圆形时的情况，亦或是未给出准确的计算方法。以上方法应用于椭圆式螺旋弹簧时，计算得出的刚度及应力值偏差过大。

本文根据椭圆式螺旋弹簧的力学模型，利用卡氏定理建立其挠度、刚度计算方法，利用半逆解法建立考虑扭转及弯曲应力同时作用的复合切应力计算方法。根据复合切应力计算方法，总结椭圆式螺旋弹簧截面复合切应力、弯曲切应力以及弹簧圈上应力分布情况和变化规律。最后，通过实例参数对椭圆式螺旋弹簧进行ANSYS仿真验证。

1 椭圆式螺旋弹簧基本参数

椭圆式螺旋弹簧在轴向的投影轮廓如图1所示。图1中，长半轴为az, 短半轴为bz,R为任意角度αz下弹簧圈的半径,O为弹簧轴心。

图1 椭圆式螺旋弹簧中径参数

椭圆式螺旋弹簧的簧丝截面如图2所示。图2中，长半轴为as,短半轴为bs,r为任意角度下簧丝的半径,O1为簧丝形心。

图2 椭圆式螺旋弹簧丝径参数

由三角函数及比例关系，可推得任意角度αz、αs下的弹簧圈半径R、簧丝半径r表达式如下：

(1)

式中:kz=az/bz;ks=as/bs。

2 椭圆式螺旋弹簧刚度计算

如图1所示，椭圆式螺旋弹簧的投影轮廓关于横轴和纵轴对称,因此只需对1/4弹簧圈进行力学分析、推导挠度关系式。1/4椭圆式螺旋弹簧受力分析模型如图3所示。

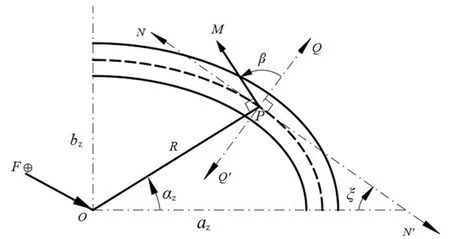
图3 1/4椭圆式螺旋弹簧力学模型

弹簧中心受竖直向下的力F, 在弹簧线圈P点上产生一个力矩M,M与P点法线QQ′的夹角为β。过P点的切线NN′与横轴的夹角为ξ, 当αz改变时，半径R、夹角β及ξ都随之改变。根据切线斜率的定义,ξ可表示为

(2)

由角与角的关系，可以推出角αz、β、ξ之间的关系如下：

β=αz+ξ。

(3)

P处的力矩M可分解为沿切线方向的扭矩T与沿法线方向的弯矩Me, 表达式如下：

(4)

根据弹性力学知识，由载荷F作用的1/4椭圆式螺旋弹簧力学模型的应变能U1可表示为

(5)

式中，J、I分别为弹簧截面的极惯性矩和惯性矩，且

(6)

则椭圆式螺旋弹簧总的应变能U可表示为

U=4NU1，

(7)

式中N为弹簧的有效圈数。根据卡氏第二定理可知，椭圆式螺旋弹簧的挠度为

(8)

由于对应变能U的公式积分化简存在一定的难度，因此利用微元法以及叠加原理对椭圆式螺旋弹簧的挠度进行计算。将1/4弹簧力学模型的π/2角度等分为90个微元角，单位微元角为Δα=π/180，则任意角度αzi可表示为

(9)

根据上述公式，可整理得到椭圆式螺旋弹簧的挠度计算式

(10)

式中v为泊松比。由式(10)及挠度与刚度的关系式，可整理得到椭圆式螺旋弹簧刚度K的计算式为

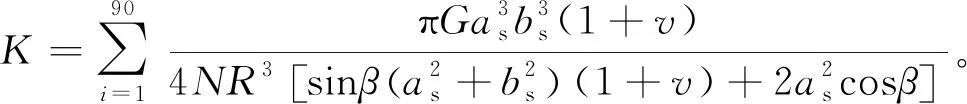
(11)

3 椭圆式螺旋弹簧复合切应力计算

3.1 扭转切应力的计算

椭圆式螺旋弹簧簧丝截面受扭转应力如图4所示。

图4 椭圆簧丝截面受扭转应力示意图

设除应力分量τ1zx,τ1zy外其余应力均为0。根据弹性力学理论[11]可知，扭转应力函数需满足微分方程和边界条件

(12)

式中T为椭圆式螺旋弹簧所受扭矩。设应力函数为

(13)

式中m为一常数，显然应力函数满足侧面边界条件。将式(13)带入式(12)中的微分方程可求得m。因此，应力函数可整理为

(14)

由弹性力学理论，可求得剪切应力分量为

(15)

式中：γ为单位长度的扭转角；G为剪切模量。根据端面边界条件可求得

(16)

式(16)中的扭转应力分量是在直杆的基础上推导出来的，若直接应用于弹簧这类大曲率螺旋线上，则会造成实际误差偏大；因此，需要引入扭转应力修正系数k对结果进行偏差修正。修正系数k[12]的表达式为

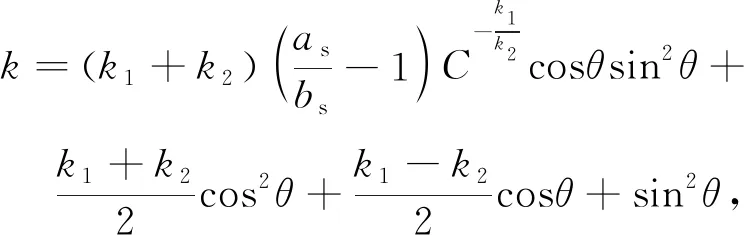
(17)

式中：C为弹簧的旋绕比,C=R/r；k1=(4C-1)/(4C-4),k2=(4C+1)/(4C+4)。

3.2 弯曲切应力的计算

弹簧所受的弯曲切应力在某些条件下不应被忽略，弹簧截面所受弯曲应力如图5所示。弹簧所受的剪力可简化为作用于圆心O1的力Fs, 受力分析后可知Fs=F。

图5 椭圆簧丝截面受弯曲应力示意图

由弹性力学理论可知，椭圆截面弯曲应力函数需满足微分方程以及边界条件

(18)

式中：v为泊松比，一般取v=0.3；Cw为常数；Ix为椭圆截面的惯性矩。为满足微分方程和边界条件，假设应力函数为

(19)

将式(19)带入式(18)中的微分方程及边界条件，即可求得mw。则弯曲应力函数可整理为

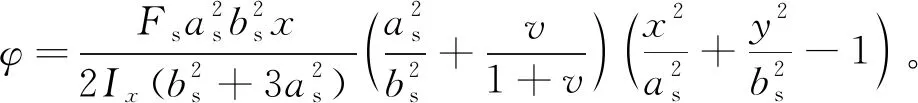
(20)

已知弯曲应力函数，由弹性力学理论，则可求得弯曲应力分量

(21)

3.3 总切应力的计算

椭圆式螺旋弹簧总的切应力应为修正后的扭转切应力与弯曲切应力的叠加之和，即

(22)

总切应力τ为

(23)

4 仿真验证

4.1 实例参数

已知某椭圆式螺旋弹簧的主要参数如下：弹簧中径长半轴az=23.66 mm、短半轴bz=18.86 mm，弹簧丝径长半轴as=4.26 mm、短半轴bs=3.34 mm，弹簧弹性模量E=206 Gpa，泊松比v=0.3，密度为7 800 kg/m3，弹簧的有效圈数为7.45，弹簧受轴向载荷F=1 950 N。

4.2 椭圆式螺旋弹簧刚度的ANSYS仿真验证

根据椭圆式螺旋弹簧的实例参数，在UG中建立其三维模型，将模型导入到ANSYS Workbench中进行静力学特性仿真。首先对模型进行网格收敛性分析，对弹簧模型一端施加固定约束，另一端施加大小为1 950 N的轴向载荷。分别对3组不同网格尺度下的弹簧挠度及应力进行仿真，结果见表1。

表1 网格收敛性分析

由表1可以看出，弹簧挠度及应力的仿真结果随着网格数量的增加几乎不变，说明仿真结果具有很好的收敛性。仿真得到的椭圆式螺旋弹簧的变形云图如图6所示。

图6 椭圆式螺旋弹簧变形云图

由图6可知，仿真得到的弹簧最大挠度为38.14 mm，刚度为51.13 N/mm。将实例参数带入式(10)、式(11)中求得椭圆式弹簧挠度及刚度的计算值。计算值与仿真值的对比结果见表2。

表2 弹簧挠度及刚度对比结果

由表2可知，弹簧挠度及刚度的计算值与仿真值偏差均在0.84%左右，表明本文建立的椭圆式螺旋弹簧刚度的计算方法是正确的。

4.3 椭圆式螺旋弹簧复合切应力的ANSYS仿真验证

根据所建立的椭圆式螺旋弹簧模型，对簧丝截面边界进行应力仿真，仿真结果如图7所示。

图7 簧丝截面应力云图

将截面实例参数带入式(23)求得截面边界应力的计算值。提取边界应力的仿真结果与计算值进行对比分析，对比结果如图8所示。

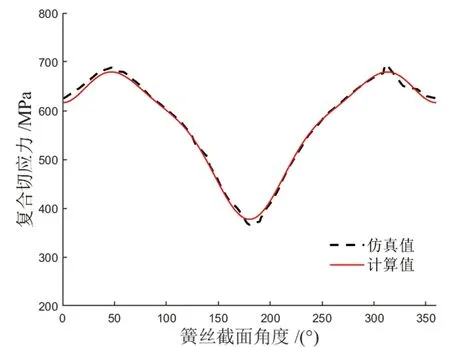
图8 簧丝截面边界切应力曲线图

簧丝边界0°、180°及最大应力所在位置313°的对比结果见表3。

表3 弹簧切应力结果分析

图8与表3的结果表明，根据式(23)计算所得应力值与仿真值趋势相同，能够较好地给出椭圆式螺旋弹簧应力分布的情况。其中，最大切应力的计算偏差在2.20%右右，表明提出的椭圆式螺旋弹簧复合切应力的计算方法是正确的。

根据给出的计算方法，对簧丝截面内部复合切应力及弯曲切应力进行计算分析，利用计算所得结果绘制如图9、图10所示的应力分布图。

图9 簧丝截面复合切应力分布图

图10 簧丝截面弯曲切应力分布图

根据图9、图10分析可知，簧丝截面复合切应力在空间的分布形似飞机状，由截面形心O1到截面边界随着半径的增大而逐渐递增，复合切应力随簧丝截面角度增加呈波浪式的变化。簧丝截面弯曲切应力并非均匀分布在截面内，其在空间的分布似双漏斗状；截面形心O1的弯曲切应力最大，随着半径的增大，截面角度0°、180°、360°位置处的应力略有下降，而约在90°、260°位置处的应力急剧减小，在此角度边界处的弯曲切应力近乎为0。

根据复合切应力计算方法，求取椭圆式螺旋弹簧表面的应力值并绘制应力分布图，结果如图11所示。

图11 椭圆式螺旋弹簧表面应力分布图

由图11可知，弹簧圈表面的复合切应力随着弹簧圈角度的增大呈余弦式变化。弹簧圈半径为中径长半轴时，即弹簧圈角度取0°、180°、360°时复合切应力最大；弹簧圈半径为短径长半轴时，即弹簧圈角度取90°、270°时复合切应力最小。

5 结论

1)对椭圆式螺旋弹簧模型进行力学分析，利用卡氏第二定理，建立了椭圆式螺旋弹簧挠度及刚度的计算方法，实现了对此弹簧挠度及刚度的准确计算。

2)基于材料力学、弹性力学理论知识，利用半逆解法建立了同时考虑扭转应力及弯曲应力的椭圆式螺旋弹簧的复合切应力计算方法，可准确计算弹簧任意位置处的复合切应力。利用此计算方法，计算并绘制出弹簧簧丝截面、弹簧圈表面的复合切应力分布图以及簧丝截面弯曲切应力的分布图，通过对应力分布图进行分析，总结出了切应力的变化趋势及分布情况。

3)ANSYS实例仿真结果表明，椭圆式螺旋弹簧刚度及复合切应力的计算值与仿真值均相吻合。其中，弹簧刚度的相对偏差在0.84%左右，复合切应力的相对偏差在2.20%左右。以上结果表明，所建立的椭圆式螺旋弹簧刚度及复合切应力的计算方法是可靠的。

4)本文所建立的椭圆式螺旋弹簧的刚度及任意角度位置处的复合切应力计算方法，经仿真验证是准确可靠的，可为椭圆式螺旋弹簧后续的优化设计及应用提供一定的理论参考。