基于图像识别的圆形指针式仪表读数矫正方法

孙志周，田克超，刘璇，王亚菲，李健，杨国庆

(1. 国网智能科技股份有限公司 机器人事业部,山东 济南 250101；2.广东电网有限责任公司广州供电局 运维部,广东 广州 510641)

智能电网是未来电网的发展方向，即在发电、输电、配电、用电等环节应用大量新技术，最终实现电网管理的自动化、综合化、集中化、智能化[1-2]。变电站作为电网枢纽必须进行定期巡视以确保安全运行，采用机器人对无人值守环境下变电站设备运行状态进行自动检测显得极其重要[3-4]。

在室外的变电站中圆形仪表是主要检测设备之一，主要分为指针式仪表和数字式仪表。对于指针式仪表，读数的准确率在很大程度上取决于圆形仪表的圆心位置。圆心定位精度越高，读数的准确率也就越高。圆形指针仪表的圆可以说是理想的圆，但由于变电站现场原因，摄像机拍摄时存在俯仰视角，不能保证拍摄的圆形仪表是正圆，造成了拍摄到的仪表图像发生了偏转变形。再者，由于摄像机视觉的影响，拍摄得到的仪表指针和真实的仪表指针之间存在差别。这些因素严重影响了指针读数识别，因此，开发一套快速、准确、稳定、可靠的读数矫正方法具有重要意义。

鉴于此，提出了一种圆形指针式仪表读数矫正方法。使用椭圆拟合方法得到圆形仪表的表盘区域并提取圆心，进而得到表针圆心和拟合得到的圆心之间的距离。结合得到的距离进行仪表指针读数矫正，输出正确的仪表读数。

1 仪表图像滤波

为了提高图像质量便于后面处理得到更好的结果，需要对图像进行预处理操作。滤波去噪是图像预处理常用的技术手段，其中，中值滤波是一种非线性滤波器，对噪声点有较好的处理效果[5-6]。

对于二维图像数据，选取一个r1×r2区域的窗口，将窗口依次滑过整幅图像，将窗口中心位置像素用窗口中像素中值代替，得到滤波后的图像。依据实践经验，选取1×3的窗口，可以较好滤除噪声点干扰,因此，结合变电站巡检图像自身特点，采用中值滤波对指针图像降噪处理。

数学形态学是进行数字图像处理的重要方法。它是建立在集合代数基础上，用集合论方法定量地描述几何形状和结构的数学方法，它逐渐成为提取和分析图像几何特征的工具[7]。数学形态学是分析几何形状和结构的数学方法，它是由一组形态学的代数运算子组成的，最基本的形态学运算子有：腐蚀(erosion)、膨胀(dilation)，开运算(opening)和闭运算(closing)。用这些运算子及其组合来进行图像形状和结构的分析及处理，包括图像分割、特征抽取、边界检测、图像滤波，图像增强和恢复工作[8-10]。

X对S的闭运算用X·S表示，其定义为

X·S=(X⨁S)ΘS，

(1)

式中：X⨁S表示X对S进行膨胀；XΘS表示X对S进行腐蚀。因此，闭操作可看作是对膨胀图像X⨁S用腐蚀来进行恢复。闭运算一般会将狭窄的缺口连接起来形成细长的弯口，并填充比结构元素小的洞。

2 表盘和指针定位提取

2.1 表盘提取

正如以上所述，对于圆形指针式仪表，识别效果的性能在很大程度上取决于圆形仪表的圆心位置。为了找到圆形仪表的圆心，首先需要定位表盘区域，根据表盘区域确定待检测仪表的圆心。由于摄像机拍摄角度的问题，变电站的圆形仪表产生了畸变，形状变为了椭圆,因此椭圆的圆心就是圆形仪表的圆心。

椭圆拟合是数据处理中的一个经典问题，它在图像处理、机器视觉、模式识别等技术领域中都有重要应用[11-12]。椭圆拟合法的基本思路是：对于给定平面上的一组样本点，寻找一个椭圆，使其尽可能靠近这些样本点[7],也就是说，将图像中的一组数据以椭圆方程为模型进行拟合，使某一椭圆方程尽量满足这些数据。椭圆拟合的常用算法有：最小二乘法拟合、Hough变换拟合、五点拟合等。

在二维平面坐标系中，椭圆一般可以用曲线方程的代数形式表示，如式(2)所示：

Ax2+Bxy+Cy2+Dx+Ey+F=0，

(2)

式中A、B、C、D、E、F为椭圆方程待确定的参数。由数学知识可知，当知道椭圆上五个点或者多于五个点的坐标即可得到方程式(2)中的参数。由于仪表发生了畸变，表盘的定位提取在人工干预的情况下效果较好,因此，本文使用五点法进行椭圆拟合，手工标定表盘区域内的五个点，以便精确地定位表盘并确定表盘圆心。如图1所示，红色的点为拟合椭圆的标定点选取方式。

图1 五点法椭圆拟合标定

2.2 表针提取

指针式仪表的指标呈直线状态，因此，在指针提取时可采用Hough变换进行直线检测。Hough变换直线检测是图像分析和计算机视觉的一个重要内容，并且Hough变换的优点是其抗噪性能比较好，并且能连接共线短直线[13-15]。Hough变换的基本思想是利用点和线的对偶性，即图像空间共线的点对应在参数空间里相交的线，在参数空间中交于同一个点的所有直线在图像空间里都有贡献的点与之对应。

在图像中检测直线的问题，其实质是找到构成直线的所有的像素点;而所有共线的点(x,y)，当直线斜率存在时，都可以用式(3)表示，其中k为直线的斜率，b为截距。

y=kx+b。

(3)

3 算法设计

机器人拍摄仪表图像时，会因为角度原因出现读数偏差，图2为同一仪表的不同角度拍摄结果。从图2中可以看到，仪表指针读数出现偏差。这是因为指针和表盘不是处于同一个平面，当仪表偏转变形时，指针相对表盘出现了偏差,因此，将指针位置平移到仪表平面上对应位置才是对应正面图像中指针的正确读数。

(a)偏转变形仪表 (b) 正面仪表

图3(a)为仪表投影俯视图简图，图3(b)为仪表投影前视图简图。因拍摄仪表目标较远，可将观测透射视线简化为平行视线。通过两张图可以观测到，当仪表旋转一定角度时，因为仪表平面与指针平面有一定间隔，从而在投影平面成像的结果会有一定的偏移；同时当旋转角度固定时，因为仪表平面与指针平面平行，两平面对应的点在投影平面成像的偏移距离相同,此时，当确定指针所在圆面圆心及针尖位置，以及表盘圆心，即可确定指针在表盘实际位置，从而获得最终矫正读数。

(a)俯视图 (b) 前视图

图3中，指针所在圆面圆心Op为标定位置，表盘圆心Oi为通过标定表盘进行椭圆拟合的位置，指针针尖Pp可通过Hough直线检测得到。根据几何知识可得到以下位置关系，进而计算出Pi的真实位置。

Pos(Pp) - Pos(Pi) = Pos(Op) - Pos(Oi),

(4)

式中Pos() 表示各点的位置坐标。

综上所述，由于仪表表盘与指针之间的距离不方便获取，但是手工标定可以得到指针的圆心位置，通过表盘椭圆拟合可以得到表盘的圆心位置。表盘区域提取步骤如下：

Step1 选择目标仪表框;

Step2 手工标定仪表盘位置(5个点均匀分布在表盘周边);

Step3 使用椭圆拟合标定数据，别截取表盘区域;

Step4 计算椭圆圆心。

图4中黄色的椭圆即为根据五点拟合的结果，其中长轴和短轴的交点(红色的点)即为表盘圆心。

图4 椭圆拟合 图5 指针和表盘的偏移

经过推算可知，表盘圆心与指针圆心的偏差即为指针针尖与表盘对应针尖位置的偏差，也就是偏转变形仪表指针读数和正面仪表指针读数的差别。见图5中蓝线即为偏移距离d。

4 实验结果及分析

4.1 实验数据获取及预处理

实验中的数据均来自机器人在巡检过程中停靠在预置位拍摄的设备图像，如图2所示。获取到的仪表图像需要进行中值滤波去噪处理，消除噪声干扰，然后使用五点法提取表盘区域进行二值化、形态学处理操作。

Hough直线检测指针提取处理过程结果如图6，步骤如下：

(a)原图 (b) 表盘 }(c) 二值化

Step1 五点法椭圆拟合。在表盘内任意选取五个点，拟合椭圆。

Step2 表盘定位截取。通过拟合的椭圆区域，将表盘区域截取出来。

Step3 滤波去噪、二值化。将截取获得的表盘区域进行滤波去噪和二值化。

Step4 形态学闭操作。对二值化表盘区域进行闭运算操作。

Step5 直线检测。使用Hough直线检测算法检测到表针的位置。

4.2 矫正实验

实验中共测试了87张图像，其中：83张图像与原图像结果一样或误差在可接受的范围内；4张图像的矫正后误差仍然不符合要求，其中，标定结果2张无法确定，2张结果较差。

表1列举了三张矫正后的读数情况，并与hough直线检测进行了对比分析，其中：图7和图8的正确误差在可接受的范围内(根据实际需求，5%的误差可接受)；图9由于仪表偏转严重，正确误差较大，误差为8.91%，矫正结果不能接受。测试结果统计情况见表2。

图9 一侧全遮挡仪表

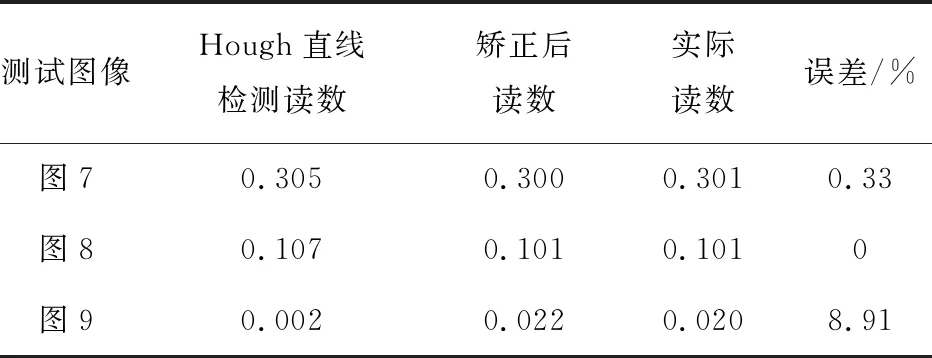
表1 本文方法结果举例

表2 测试结果统计

表1中数据显示，矫正后的读数和实际读数更加接近，更加优于Hough变换得出的读数。表3中使用透视变换对图像进行矫正，然后识别指针对数。测试结果发现对偏转较小的效果较好，如图8结果和本文一致，但对偏转角度较大的情况识别结果误差仍然较大,这主要是因为图像偏转严重，即使矫正后仍有几何位置差异。本文算法中图9错误主要是表盘提取不完整造成了表盘圆心及偏移距离计算出现偏差。

表3 透视变换矫正结果举例

实验结果表示，本文矫正算法使仪表读数的正确性取得了很大的改善。利用指针和表盘的偏移距离矫正，提高了偏转仪表的读数正确率，正确率达到了95.4%。

5 结论

1) 该算法成功解决了变电站设备中圆形指针式仪表倾斜造成算法识别率降低的现象，正确率达95.4%，提高了变电站巡检机器人设备识别性能，可应用到产品中。另一方面，算法具有建模简单、运行速度快、鲁棒性强等特点，算法的成功实施推进了变电站无人值守进程。

2) 对偏转较大造成遮挡严重的仪表读数还存在偏差，仍需进一步分析研究，如针对硬件设备，调整机器人停靠位置、优化云台俯仰角度控制等，针对算法需要进一步研究高性能的仪表圆心定位方法。