解析几何教学中如何有效落实逻辑推理素养的培养

王小飞

(江苏省如皋市长江高级中学 226500)

学生数学能力的发展要以逻辑推理素养为基础和前提，同时这也是数学核心素养培养的关键构成部分，对学生发展意义重大.基于此，我们借助高中数学中的重要知识内容——解析几何，对培养高中生逻辑推理素养的内容展开了论述研究，为构建高质量数学课堂奠定基础.

1 逻辑推理素养培养的意义研究

随着核心素养概念的提出，要求高中数学课程中积极体现核心素养的内容，彰显数学学科的品质与基本特征，强调学生价值观、情感与态度的综合强化与培养，这是在学习与应用数学时渐渐构成与发展起来的.当前，在数学学科核心素养中逻辑推理素养属于关键性内容，其基本表现为：基本规则与形式的掌握，寻找问题与给出命题，进行论证过程的探究与表述，认识命题体系，逻辑清晰的交流与表达.

推理逻辑、空间想象以及计算等是学生数学能力的主要构成，其中，推理逻辑能力的强化将进一步促进其余二者的发展，他是学生学习数学知识中的重要能力体现.

在学生的生活与学习中逻辑推理思想发挥着重要作用.高中数学解析几何教学中培养与发展学生的逻辑推理素养，可以引导学生展开逻辑推理思考，引导学生发现问题，思考问题，解决问题，通过解析几何教学中培养学生逻辑推理素养，引导学生更加高效的学习解析几何知识内容，实现知识的发散与升华；逻辑推理素养的掌握，引导学生在平时生活、数学学习以及活动中将自己的方法更好的表达出来.引导学生彼此间相互合作与交流，激发学生学习热情，强化学生的实践与创新能力.

2 解析几何教学中培养学生逻辑推理素养的方法

在高中数学知识的学习中，解析几何属于其中的重、难点内容，并且在考试中所占据的分值比例较大，一旦学生在学习中没有掌握一套行之有效的方式方法，或者没有形成逻辑推理能力，将会在这部分知识的学习中遇到很大的困难.逻辑推理是数学体系建构、数学理论获取的重要方式之一，是保证数学严谨性的重要学习思想，是在数学活动中人们互相交流的基本思维形态，对此，我们需要深刻把握高中解析几何知识教学中培养学生逻辑推理素养的契机，不断强化学生这方面的能力与素质.

2.1 逻辑思维强化

培养高中生的逻辑推理素养，需要严格的要求其思维发散能力，尤其数学思想建模中，要密切关注数形结合对学生逻辑推理素养的影响.由于传统课堂授课理念与模式已经难以满足当前教学的需要.因此，教师需密切关注新课改的规定，在养成学生的逻辑推理素养中，引导他们探索逻辑关系，找寻其中的奥秘，在教学解析几何知识中，这种解题方法较为常见.通常而言，在对这类试题解答中，先把一个常数设定出来，再接触变换消除方法，实现求解.在解析几何试题解答中渗透此方法，需要充分考虑下列内容：①科学控制参数.通过引入参数的方式展开试题讲授，达到横跨解答的目的.因此，授课中应该科学的控制参数，以防引入不正确的参数而将题目解答难度提升.②易懂简易参数的选取.在引入参数中，不仅要考虑到试题的难易情况，而且时刻坚持简单实用的原则，把与解析几何相符合的参数引入当中；③消除要方便.参数引入后，需要引导他们快速消除参数，化简试题，在思索参数是否影响正常量与未知量的情况下进行消除，避免盲目引入参数而影响最终学习质量.

2.2 培养问题思维，强化逻辑素养

在平时授课中，需要积极发挥典型例题的引导作用，通过较强探索性的试题引领学生寻找问题源泉，并渗透数学思想进行作答，进而把数学的魅力呈现在学生面前，引导学生积极、主动的探索问题，将学生创新意识以及解题能力不断提升.同时，在问题得到处理后，合理的总结与反思可以让学生更好的理解知识内容.只有对思维过程的不断反思，总结解题方式，对于解题中的问题才能及时发现.摆脱题海战术展开数学知识学习，要求教师精简处理试题，将具有代表性的题目呈现在学生面前，通过深入引导学生探究分析，不断内化与结构化处理知识内容，深化学生的数学思想.

例1 经过点A(1,3)、B(4,2)、C(1，-7)的圆与y轴相较于M，N两点，求|MN|？

在分析这道题目中，通过给出的3个点，在确定了圆的基本方程式后，求出y上它的截距.经过分析此题目，可以通过以下步骤求解圆方程表达式：第一步，先把AB、BC的垂直平分线方程写出来，之后按照现有条件将两条直线交点求出来，这样随之也就确定了圆的半径、圆心以及最终的方程.第二步，向(x-a)2+(y-b)2=r2中依次带入圆的标准方程，并将圆的方程表达式在此基础上进行求解.第三步，将圆的一般方程求解出来.因为这三种方法不够清晰直接，并且自身弱点都比较明显，而且对于题目所呈现的数据关联性难以准确分析.因此，制定更加高效的方法非常重要.

解析KAB=3-2/4-1=1/3，KBC=2+7/4-1=3，所以，KAB·KBC=-1.

对以上陈列的解析方法的分析，不论通过何种方式确定圆，需要先确定圆的圆心和半径.所以，对此试题解答中，发散学生思维，科学引导其逻辑探究，采用合适的方式让学生将圆心与半径确定出来，在仔细分析与思索后，借助数形结合的方式简化问题，之后利用KAB·KBC=-1能够推出AB与BC相互垂直，之后推导出直角三角形外接圆的圆心在AC这条斜边中点上，经过有效的转化三者间的关系，简化处理繁琐的计算，把握基本问题，最后得出最终的答案.

2.3 设置开放性问题，调动学生逻辑推理能力

在传统的授课之中关注数学技能与知识的常规运用，忽略了如何创设开放性问题情境.伴随全新教育改革的推进，注重从生活中挖掘知识，在教授知识中融入了很多数学运用题目，从某种程度上深化了学生数学运用素养的提升.然而，通过处理相关问题得知，学生较为擅长数学技能与知识的常规运用，但是在复杂的问题情境内不善于处理问题.因此需要教师将一些开放性、真实性的问题情境创设出来，在这种疑惑的引诱下去推理论证，这样的效果会更加理想.

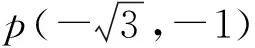
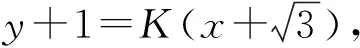
通过具体问题内容的创设，构建具体的模型思维，然后向解析几何的具体授课内容中渗透，让学生以更加饱满的热情去学习，对数学知识进行更加直观的感知，对有关内容进行深入理解，捋顺解题思路，积极思索问题，灵活运用相关知识点，强化逻辑推理素养，不断强化课堂学习效率与质量.

2.4 借助逆向思维，培养学生逻辑推理素养

高中数学解析几何比较抽象，通过实践教学让学生深入理解解析几何知识内容，从而达到理论与实践的融合.例如，在教学《直线和抛物线的位置关系》中，围绕这样一道题展开教学引导：在y2=4x的抛物线焦点处作一条斜率为1的直线L，同抛物线交汇于A与B两点，求弦AB的值.

解析通过抛物线方程可以计算得出焦点的具体坐标，通过给出的直线斜率，进而能够得到直线L的方程，进而联立起抛物线方程与直线方程，进而得到A和B点的具体坐标，通过两点间距离计算公式，能够得到AB的绝对值.此种解答方式较为简易，但是代数运算相对复杂，尤其遇到参数时，为了让运算变得简单化，通过韦达定理将弦长求解出来，亦或者利用数形结合简化计算过程.

为了在逆向思维中培养学生的推理逻辑素养，在完成解答后，学生对基本的解答方法理解与掌握后，在将AB的绝对值求出后展开变式练习，还是在这个抛物线经过斜率为K的直线，同抛物线相交于AB两点，弦长为8，求出直线的斜率值.为学生留设足够的时间去比较变式与原式间的关系.尽管原题与变式考察的内容差不多，但这是一个逆向的思维过程，若是学生深入探究，进行比较，这样就可以掌握以及灵活应用本题所涉及的知识内容.

总的而言，在高中解析几何教学中强化与培养学生的逻辑推理素养，对教学质量的提升与学生自身成长的强化都会带来巨大帮助.在解析几何知识模块具体教学引导中，需要从多方向切入培养学生的逻辑推理素养以及思维解题能力.在推理与学习基础知识期间，要引导学生从已知向未知推理探究，不断强化其逻辑推理素养，在具体的授课中也要注重学生思维模式的强化，引导他们在自主学习期间优化自身的思维方式，通过多样化的引导与强化，在教学中不断变化试题内容，进而在强化学生思维的同时将逻辑推理能力和素养不断提升.