单向通道行人-自行车混合流建模及自组织现象研究

郝妍熙，刘戎阳，胡华，方勇，刘志钢

(上海工程技术大学，城市轨道交通学院，上海 201620)

0 引言

步行和自行车是重要的交通方式，是出行者最后一公里的主要选择，可以促进城市交通领域节能减排，预防和缓解城市交通拥堵，促进城市交通资源合理配置。三部委联合发布的《加强城市步行和自行车交通系统建设的指导意见》中提出，我国行人和自行车混合交通在交通系统中占比的发展目标为55%[1]。因此，深入解析行人与自行车混合流的运动特性非常重要。通过对实际混合流的观察分析发现，骑行者和行人的混合流动在空间维度上往往表现出自组织行为。研究行人和骑车人混合流的自组织特征可以为行人-自行车混合流的运动特性研究与仿真建模提供理论基础，为混合流交通组织提供有效依据。

目前具有代表性的行人、自行车微观仿真模型有元胞自动机模型、社会力模型、启发式模型等。Jiang等[2]对自行车流的元胞自动机模型进行修正，定量再现了基本图和临界密度以上交通堵塞的发生情况；Ning等[3]基于启发式模型，用3个圆来代表自行车，通过有碰撞模型和无碰撞模型的启发式算法，确定自行车和行人的运动方向和运动速度。社会力模型最早由Helbing等[4]提出，主要应用于行人领域的仿真研究。张蕊等[5]对社会力模型进行修正，结合颗粒流理论，引入社会关系强度，实现了行人结伴行为的仿真；丁青艳等[6]在模型计算时引入矩形作用范围，提出避免过度重叠的行为规则模型。社会力模型同时也应用于非机动车微观仿真[7]。张蕊等[8]基于社会力模型，引入骑行者生理感知空间并结合颗粒离散元理论，改良了自行车之间的接触力、自行车与边界的作用力；严巧兵[9]通过给社会力模型添加感知域和超越力来实现自行车超越行为；马尚[10]通过对非机动车道或人行横道边界在非机动车占道超越不同阶段的特点改进社会力模型实现非机动车占道超越；王占中等[11]考虑自行车对行人过街的干扰，引入自行车与行人以及自行车与人行横道间的相互作用。

1 模型构建

假设行人所需的最小舒适空间由1 个圆组成，骑行者所需的最小舒适空间由3 个圆构成。行人圆的半径为rp，自行车圆的半径分别为r1、r2、r3，行人的质量为mp，自行车及骑行者的总质量为mb。

1.1 行人社会力模型建模

以行人i为目标主体的社会力模型为

式中：fi(0)为吸引个体接近目标的力，即行人的自驱动力；fi(e)为个体间和个体与环境间的排斥力和相互作用力。

行人i的自驱动力为

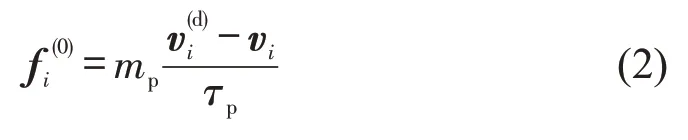
式中：v(id)为行人的期望速度；vi为行人的当前速度；mp为行人的质量；τp为行人的松弛时间。

行人i会受到来自前方180°范围内其他行人j、自行车a和环境的相互作用力fij、fia和fiw，即

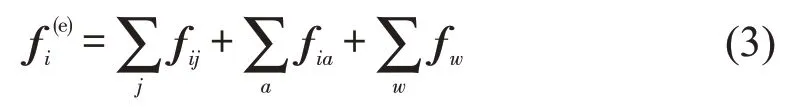
行人之间存在排斥力和接触力，即

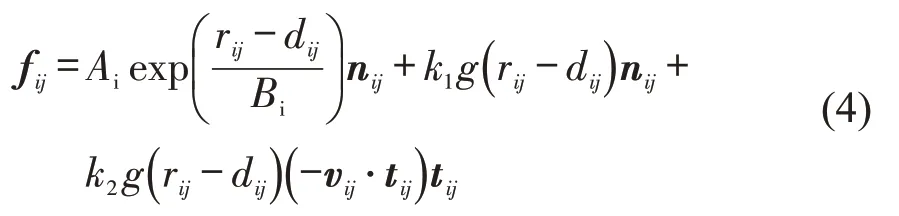
行人与环境之间的作用力相似，即

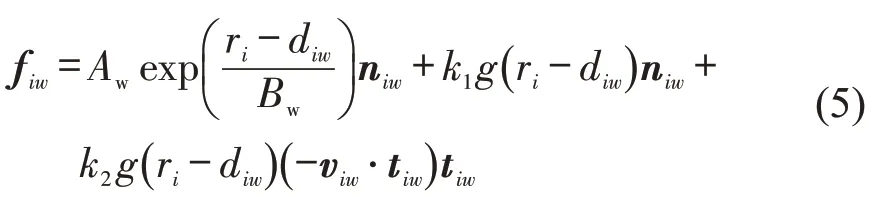
由于自行车的灵活程度不如行人，自行车的圆与其他个体的圆接触极易发生事故，所以一般行人和自行车、自行车和自行车之间不存在接触力，只有排斥力[9]。自行车由3 个圆组成，每个圆都会对行人产生排斥力，即

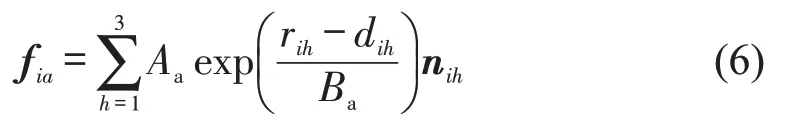
式中：Ai、Bi分别为行人之间相互作用强度和作用范围；Aw、Bw、Aa、Ba分别为行人与环境、行人与自行车相互作用强度和作用范围；k1、k2为常数；g(x)=max{0,x}；rij为行人i和j的半径之和；dij为两个行人中心的距离；vij为行人i和j之间的相对速度，vij=vi-vj；nij为从行人j指向行人i的单位向量；tij为垂直于nij的单位向量；ri为行人i的半径；diw为行人i和环境(边界)的垂直距离；niw为边界上距行人i最近点指向行人i的单位向量；viw为行人i与边界的相对速度；tiw为垂直于niw的单位向量；rih为行人i和自行车a第h个圆的半径之和；dih为行人i和自行车a第h个圆中心之间的距离；nih为自行车a第h个圆中心指向行人i中心的单位向量；h为自行车a前进方向的第h个圆。

1.2 自行车社会力模型建模

以自行车为目标主体的社会力模型为

式中：fa(0)为吸引个体接近目标的力，即自行车的自驱动力；fa(e)为个体间和个体与环境间的排斥力和相互作用力。

自行车a的自驱动力为

式中：v(ad)为自行车的期望速度；va为自行车的当前速度；τb为自行车的松弛时间。

自行车会受到来自行人、其他自行车、环境的相互作用力fai、fab、faw，即

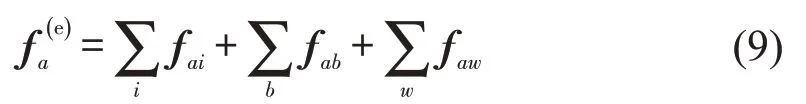
由于自行车由3个圆构成，其受力与运动方式与单个圆的行人不同，在此做以下假设。

假设1 自行车3 个圆中，3 个圆均为钢节点连接，自驱动力的作用点为前进方向第1 个圆的圆心。

假设2 自行车3 个圆均会对其他个体造成影响，但只有前2个圆受到其前方180°范围内其他个体的影响，如图1所示。中间的圆是行人所在位置，行人无法观察到后方的其他个体，因此不受后方个体力的影响。

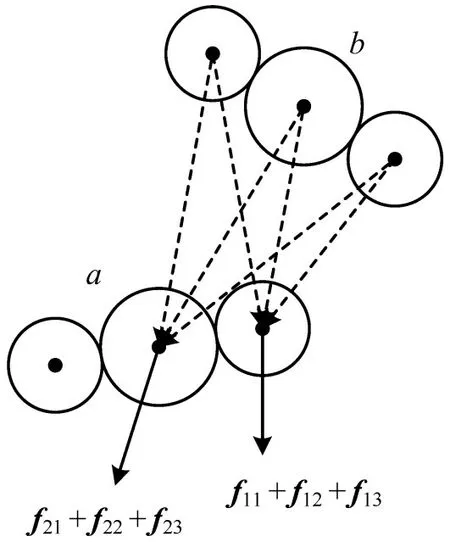
图1 自行车与自行车之间相互作用力示意图Fig.1 Schematic diagram of interaction force betweenbicycle and bicycle

假设3 自行车发生转动时，转动中心为前进方向最后一个圆的圆心。

假设4 自行车本身的质量分布是均匀的，骑行者的质量全部集中在自行车中心。

自行车和行人之间的相互作用力为

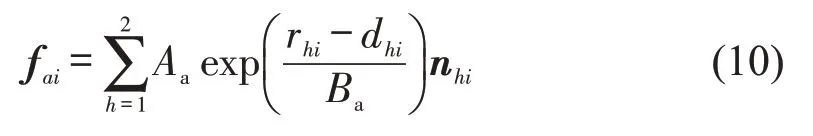
自行车与自行车之间的相互作用力为

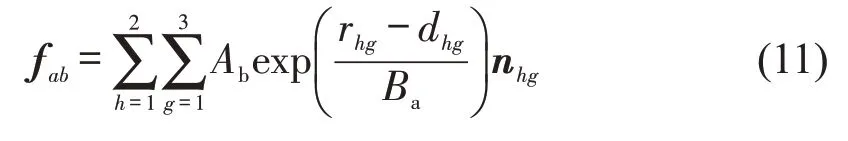
自行车与环境的作用力为

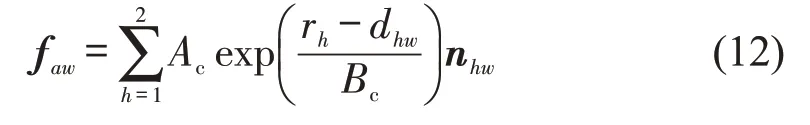
式中：Aa、Ba为自行车与行人之间相互作用强度和范围；Ab、Bb、Ac、Bc为自行车与自行车之间、自行车与环境之间相互作用强度和范围；rhi为行人i的半径与自行车a前进方向第h个圆的半径之和；dhi为行人i和自行车a前进方向第h个圆的距离；nhi为i行人指向a自行车前进方向第1个圆的单位向量；rhg为自行车a第h个圆的半径与自行车b第g个圆的半径之和；dhg为自行车a第h个圆与自行车b第g个圆中心的距离；nhg为为自行车b第g个圆指向自行车a第h个圆中心的单位向量；rh为自行车a第h个圆的半径；dhw为自行车a第h个圆距边界的垂直距离；nhw为边界上距自行车a第h个圆最近点指向自行车a第h个圆中心的单位向量；h为自行车a前进方向的第h个圆；g为自行车b前进方向的第g个圆。

在基于社会力模型的自行车仿真中，部分学者把自行车抽象为一个椭圆[7]，对其整体进行受力分析，将其作为特殊的行人，忽视了自行车不同部分受力的差异。以椭圆的中心为旋转中心转动，则导致自行车尾部向转动的反方向发生较大的侧向位移，显然是不符合现实情况的。本文用3个圆来代表自行车，前进方向前2个圆收到其他个体及环境的作用力，以第3 个圆为自行车的旋转中心，优化了自行车的旋转。本文模型中自行车发生转动时，旋转的中心为自行车前进方向的第3个圆的圆心，自行车尾部不会发生侧向位移，如图2所示。

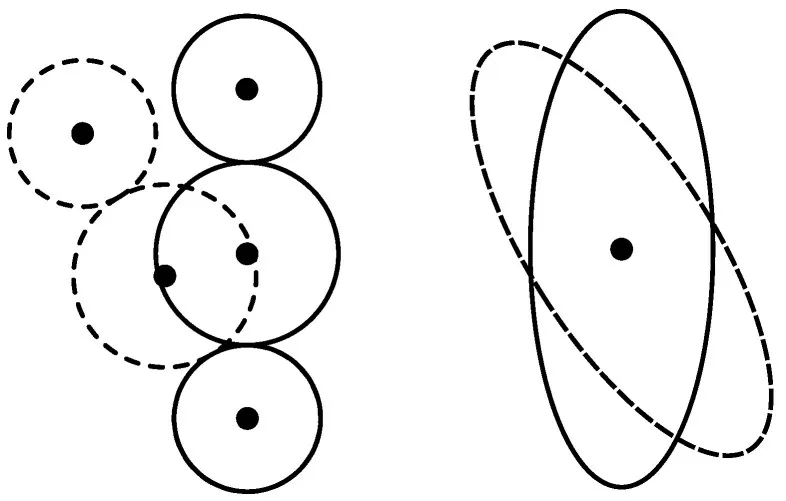
图2 三圆与椭圆的偏转示意图Fig.2 Schematic diagram of deflection of three circles and ellipses

根据假设1，本模型自行车为刚性连接，自行车3个圆的圆心始终在一条直线上。根据假设2和假设3，前2个圆车身方向上(前进方向)的合力带动自行车向前位移，垂直于车身方向上的两个分力带动自行车偏转，距旋转中心的距离分别为r2+r3、r1+2r2+r3，如图3所示。

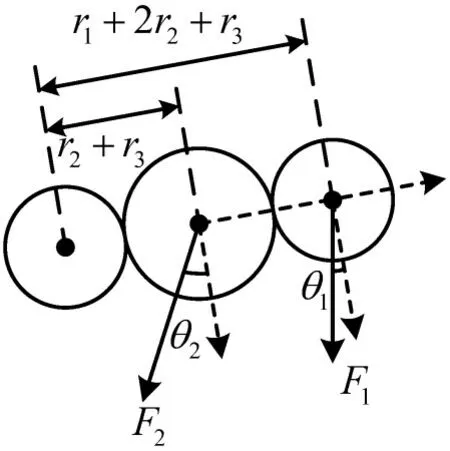
图3 自行车受力偏转示意图Fig.3 Schematic diagram of bicycle deflection under force

自行车旋转运动方程为

式中：I为自行车转动惯量；ω为角速度；T为总力矩。

I计算公式为式

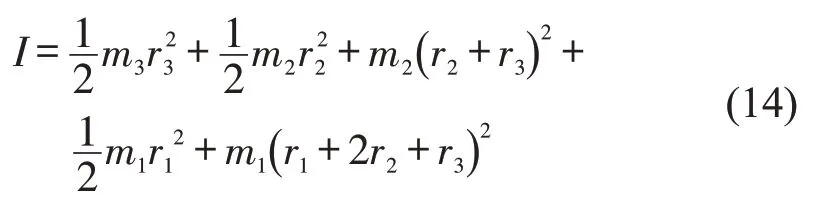
中：m1、m2、m3为自行车3 个圆的质量，根据假设4，m2包含了骑行者的质量。

令前2 个圆受到的力总和分别为F1、F2，则T的计算公式为

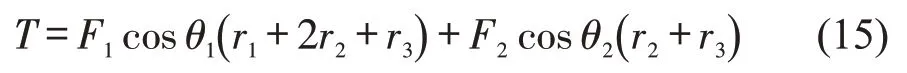
式中：θ1为F1与车身方向垂线的夹角；θ2为F2与车身方向垂线的夹角。

2 数据采集与处理

本文选取一段实际行人-自行车混合直行通道进行观察，此通道由锥形桶分割成两个单向通道，左侧通道为本文实验通道，宽度为5.4 m。经视频观察发现，在行人和自行车流较长时间连续稳定进入通道的情况下，通道内会有稳定的“车道”形成，行人在右侧“车道”行走，自行车在左侧“车道”移动，如图4所示。总体来看，行人和自行车会形成明显的“车道”，当行人和自行车比例发生变化时，“车道”宽度会发生变化。

图4 自组织现象Fig.4 Self-organization phenomenon

根据实际调查，行人质量主要分布在50～80 kg，为方便计算骑行者和自行车整体的转动惯量，行人质量取65 kg。通过视频统计分析得出，行人的自由流速度在1.1～1.4 m·s-1之间，自行车的自由流速度在4.5～6.0 m·s-1之间，自由流速度作为期望速度。速度提取过程如图5所示，选取实际通道中两条显著标记线，测量其标记线间隔为17 m，通过视频观察对象经过两条标记线的时间差，间隔除以时间差即为测定对象的速度，选定行人和骑行者数量较少、不受干扰的时间段进行观测，此时间段内速度即为自由流速度。通过对多种自行车的实际测量，发现其车身总长度与Ning 等[3]中调查的1.4 m 相符，故本文选取1.4 m 作为自行车车身长度。自行车质量参照严巧兵[9]调查的15 kg，根据假设4，自行车质量均匀分布，结合3个圆的半径可推得3 个圆的质量m1、m2、m3分别为4.65，70.7，4.65 kg，则根据式(13)可计算出骑行者转动惯量的值为22.5931。

图5 速度提取示意图Fig.5 Schematic diagram of speed extraction

本文使用Matlab 软件进行仿真，仿真通道宽5.4 m，根据既有研究的取值，结合实际调查数据和多次仿真验证，最终相关参数取值如表1所示。

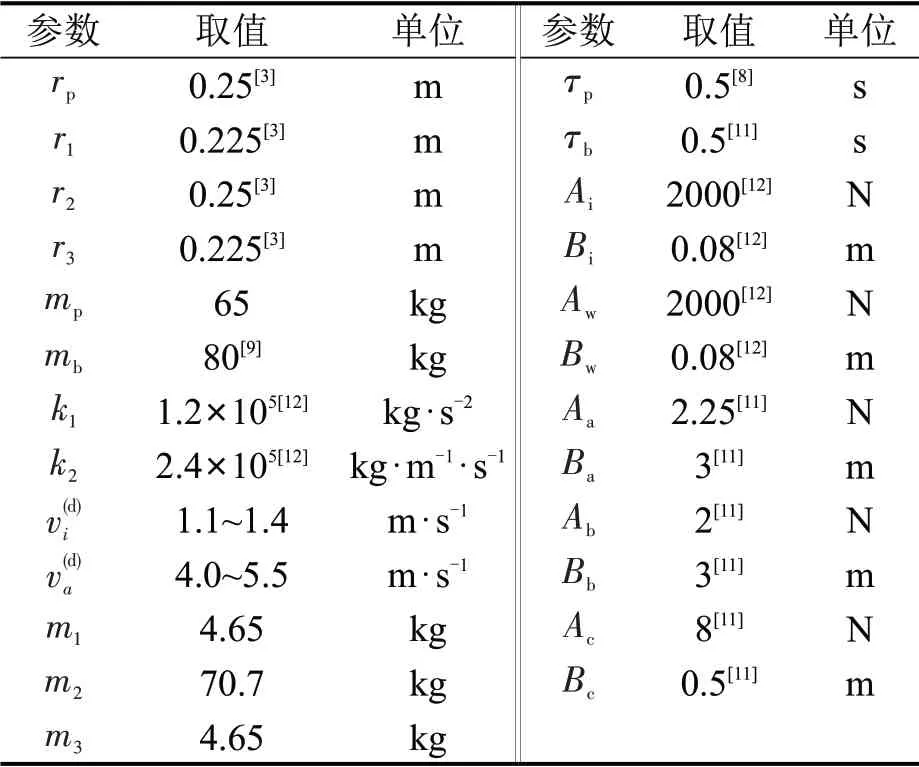
表1 参数选取Table 1 Parameter selection

3 仿真与结果分析

3.1 模型可靠性验证

为验证模型的可靠性，本文对实验和仿真数据进行采样，得到行人和自行车的流量-密度关系，并拟合成曲线，结果如图6和图7所示。图6为自行车实际与仿真的流量-密度基本图对比，R2为0.8689；图7为行人实际与仿真的流量-密度基本图对比，R2为0.8961，仿真效果较好。

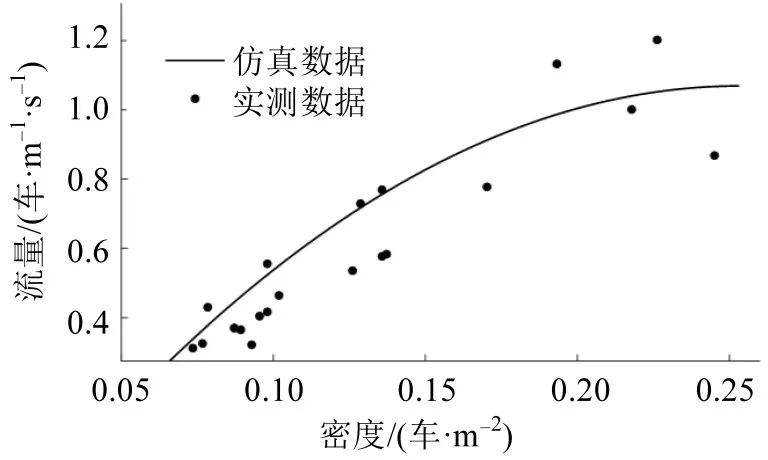
图6 自行车基本图Fig.6 Basic bicycle diagram

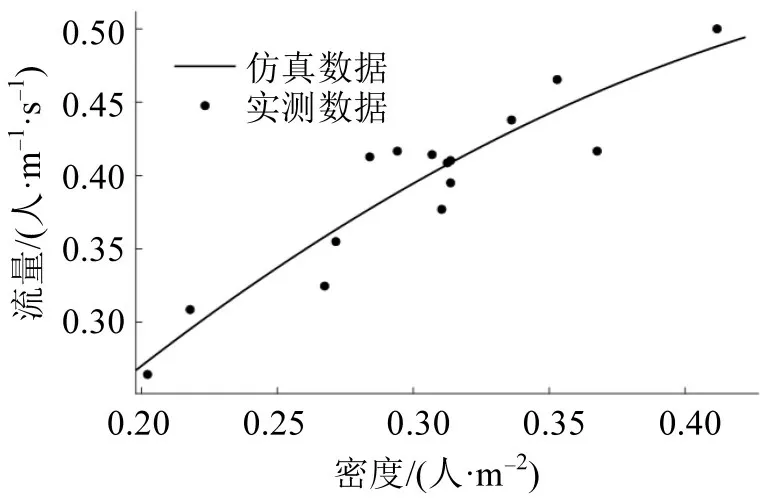
图7 行人基本图Fig.7 Basic pedestrian diagram

3.2 自组织现象及特性分析

在仿真中，当行人和自行车前进方向相同时，设置行人遇到障碍会向右避让，自行车遇到障碍会向左避让。仿真开始时，行人和自行车混合分布在通道入口处，在一定时间后，也出现了自组织现象，如图8所示。

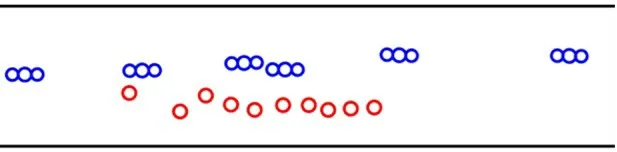
图8 仿真模拟中的自组织现象Fig.8 Self-organization in simulation

行人和自行车往往倾向于在各自车道中线处移动，本文用通道内所有行人与自行车的距左边界的平均距离来表征车道宽度的大小，自行车距左边界平均距离越小，则自行车车道宽度越小，反之则越大；行人距左边界距离越小，则行人车道宽度越大，反之则越小。图9为行人和自行车数量为1∶1时，车道宽度随时间的变化情况，从图中可以看出，自行车的车道变化略慢于行人，且自行车所占用的车道宽度大于行人。当自行车与行人间有明显的车道形成后，行人车道偏向于稳定，自行车由于整体速度较快，且速度浮动区间较大，因此车道宽度变化幅度较大。

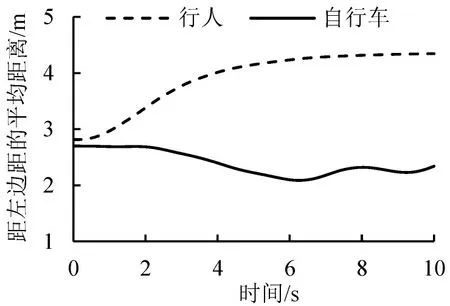
图9 自行车、行人距左边界的平均距离Fig.9 Average distance between bicycles and pedestrians from left boundary

实际观察发现，行人和自行车的密度、比例不同时，其车道宽度也会发生变化。图10(a)为相同行人/自行车比例，不同密度情况下，自行车距离边界的平均距离，其中0.20，0.17，0.14 m-2为自行车的密度。随着行人密度和自行车密度的改变，行人车道宽度变化不大，自行车车道在一定程度上受到密度影响，自行车密度越大，车道宽度越小且波动越大。图10(b)为不同行人/自行车比例下，自行车车道宽度的变化。当行人和自行车的比例为1∶2时，自行车距左侧边界距离更远，即占据了更宽的车道；当比例增加到1∶1时，车道宽度逐渐变小；当比例增加到2∶1 时，自行车车道宽度变得更小，由于占用空间减小，自行车与其他个体的冲突增多，车道宽度波动更加明显。

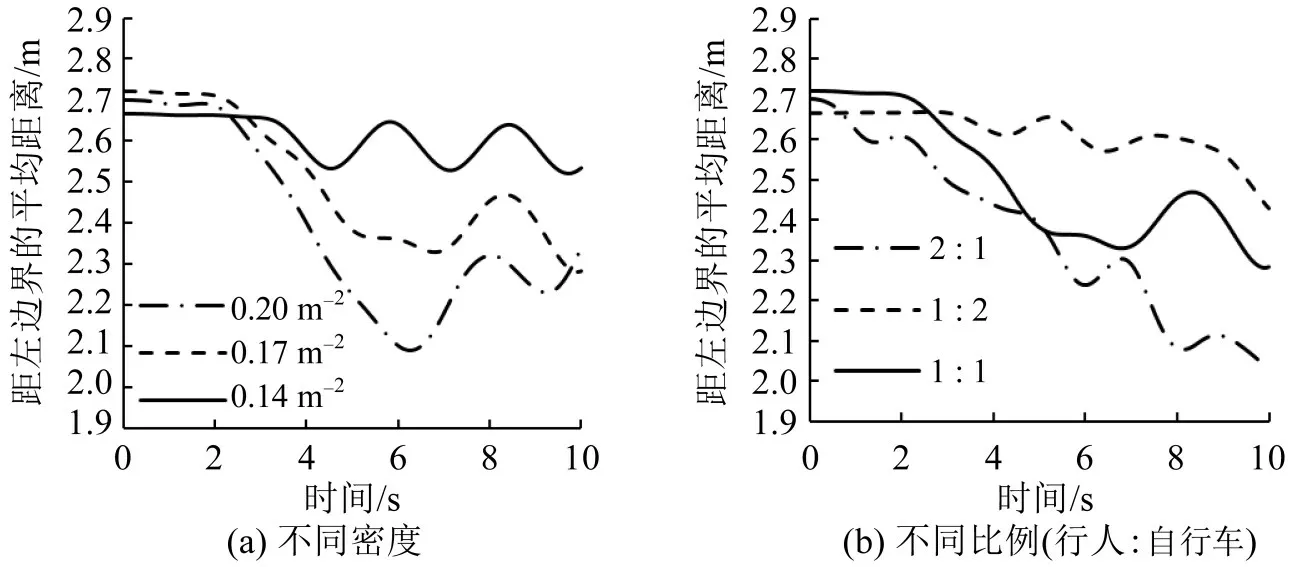
图10 自行车、行人距左边界的平均距离Fig.10 Average distance between bicycles and pedestrians from left boundary

总体来看，行人/自行车比例为1∶1 时，随着自行车密度增加，自行车车道宽度的波动也增加；当自行车比例逐渐减小时，自行车所占车道宽度也随着减小，且车道宽度的波动增大。

在自组织现象出现之后，如果行人和自行车的输入稳定，车道也保持稳定状态。根据实际观察，行人的输入往往是不稳定的，会出现一段时间内行人输入较少或者没有行人输入的情况，从而导致行人在通道上分布不连续。在自行车向前移动的过程中，遇到行人会倾向于向左避让，如果通道某一部分没有行人，自行车缺少向左的约束，会向右移动进行松弛，使得某一段车道变宽，如图11所示。由于发生变化的这部分车道在空间上是不停向前移动的，难以单独进行研究，本文依旧用自行车的整体距左边界的平均距离来表征车道宽度，单独发生变化的这部分车道也会影响整体车道宽度的变化，并与之正相关。如图12所示，当车道已经稳定形成后，行人暂停输入，自行车车道宽度一开始变化不大，随着时间推移，其车道宽度显著增加。

图11 不同宽度的虚拟车道Fig.11 Virtual lanes with different widths

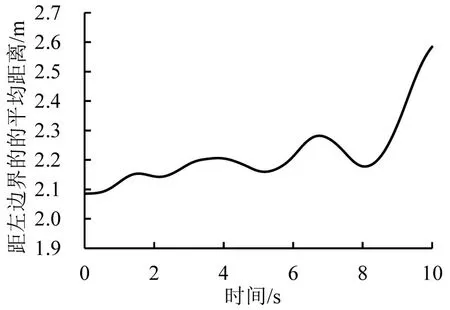
图12 行人输入暂停时自行车距左边界的平均距离Fig.12 Average distance between bicycle and left boundary when pedestrians enter a pause

4 结论

本文得到主要结论如下：

(1)提出了一种面向行人-自行车混合流的混合流社会力模型，并修正了已有研究中的自行车模型。通过实测数据与仿真数据对比，验证了模型的有效性。

(2)仿真结果表明，在共享道路中，行人与自行车混合流会出现自组织现象，分别形成车道，当行人和自行车数量比例为1∶1时，自行车会占据更多的道路空间，行人车道宽度较为稳定，自行车车道宽度波动比行人大。

(3)在行人和自行车数量比例为1∶1的前提下，自行车密度越大，自行车车道宽度越小且波动越大，密度越小，自行车车道宽度越大且稳定；自行车比例越小，自行车车道宽度越小且波动越大；自行车比例越大，自行车车道越大且越稳定。

(4)在行人和自行车车道宽度稳定后，行人输入中断，一开始自行车宽度增长幅度不大，一段时间后，自行车车道宽度显著增加。