微型离心泵模化试验方法及数值模拟研究

赵子涵，包宁，王胜，邵春雷

(南京工业大学机械与动力工程学院，南京 211816)

在医学上微型离心泵常用于血液的输送，许多学者在对微型离心泵进行试验研究时选用与血液粘度相似的水和甘油混合物作为替代介质[1-2]。但是这种试验方法仍存在一定的不足，在试验前需要配置密度为1 055 kg/m3，粘度为0.003～0.004 Pa⋅s的水和甘油混合溶液，试验准备时间长，需购买甘油溶液与粘度测量仪，试验成本较高，试验结束后，仍会有水和甘油依附在试验装置表面，清理困难。本文拟采用水来替代血液作为试验介质，通过模化方案设计模型泵进行试验并换算得到原型泵的性能。

国内外运用模化试验方法对不同的泵进行了研究。张根广等[3]通过不同流体对泵的相似性进行试验验证，发现模型泵和原型泵具有很好的相似性，并且采用黄原胶溶液模拟血液流体，发现黄原胶溶液模拟血液流体时的相似性更好。方向阳等[4]建立了熔盐泵输送固液两相流的相似准则，根据其所设计的熔盐泵模型试验方案，对熔盐泵内部流动进行了数值模拟，采用高速摄像技术对泵内盐析两相流动状况进行了拍摄，研究了颗粒直径和密度对熔盐泵外特性与内部流动的影响。SHAO等[5]研究了熔盐泵的无量纲特性，提出一种使用水代替熔盐进行建模试验的方法，并采用经过验证的数值方法对模型进行模拟，并对熔盐泵的性能进行了详细的研究。前人对微型离心泵也开展了相关研究，但主要集中在内部流动研究[6-8]、空化研究[9-11]、改变结构提升性能[12-14]等方面的研究。微型离心泵输送水时，可以通过调节工况得到与输送血液时相似的内部流动状态，并通过换算得到输送血液时的外特性，这样可以大大节省时间与成本，因此有必要对微型离心泵进行模化试验研究。

本文通过量纲分析建立微型离心泵相似准则，确定模化方案。将相似理论推算的结果与数值模拟结果进行比较，验证相似理论和模化方案的正确性；研究原型泵和模型泵压力和速度随时间的变化规律，通过判断原型泵和模型泵压力和速度变化规律是否相同，进一步验证模化方案的正确性。研究结果可为微型离心泵内部流动及外特性试验提供一种简便经济的新方法，也可为其它泵的模化试验研究提供参考。

1 三维模型及网格划分

微型离心泵叶轮直径为47 mm，进口管直径为15 mm，出口管直径为20 mm，定义叶片和蜗舌夹角为α，并在蜗壳Ⅰ-Ⅷ截面上设置监测点，微型离心泵蜗壳截面及监测点如图1所示。采用ICEM软件对微型离心泵进行网格划分，微型离心泵的进口段和出口段采用结构化网格，叶轮和蜗壳部分采用非结构化网格并进行局部加密，微型离心泵计算区域网格如图2所示，当网格数从875 455增加到1 612 943时，微型离心泵的外特性几乎没有变化，限于篇幅，此处不再详述。本文选用875 455的网格数进行数值模拟。

图1 微型离心泵蜗壳截面及监测点

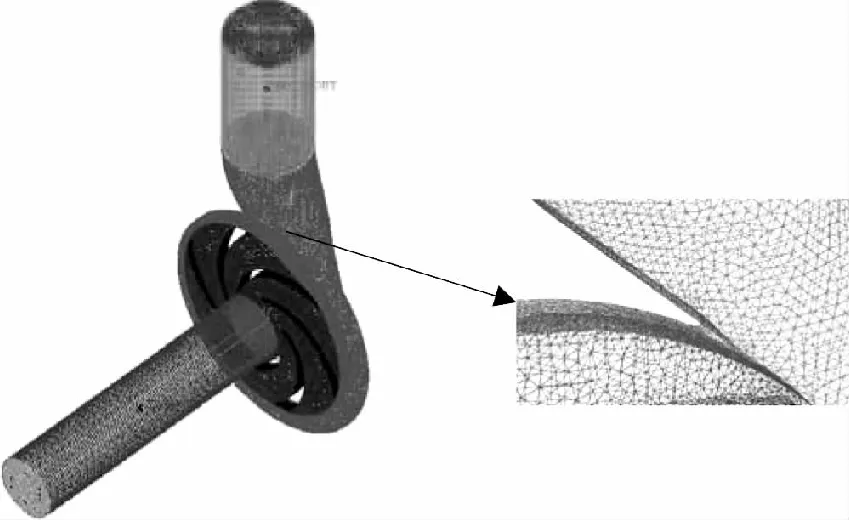
图2 微型离心泵计算区域网格

在人的正常体温下，血液粘度为0.003～0.004 Pa·s，本文取0.003 4 Pa·s，血液密度约为1 055 kg/m3，正常成年人的血液流量为3～5 L/min，血压范围为80～120 mmHg[3]。本文微型离心泵的额定工作流量Q为0.3 m3/h，额定工作转速n为2 300 r/min。

2 微型离心泵模化试验方法研究

2.1 微型离心泵输送粘性介质无量纲特性分析

根据相似理论对微型离心泵输送血液进行无量纲特性分析，微型离心泵输送粘性介质涉及到的物理量有泵的转速n，泵的流量Q，泵的特征尺寸D，比能量gH，输送介质的密度ρ，输送介质的动力粘度μ。根据π定理，可将上述物理量进行描述如式(1)[5]。

f1(n，Q，D，gH，ρ，μ)=0

(1)

上述涉及到的物理量中一共含有3个基本量纲，分别为时间T、长度L以及质量M，通过量纲分析可以导出3个独立的相似准则，可以将式(1)表述如式(2)所示。

f2(π1，π2，π3)=0

(2)

同时选择泵的转速为n、泵的特征尺寸D、介质的密度ρ作为基本物理参数，根据量纲和谐原理可得到式(3)～(5)。

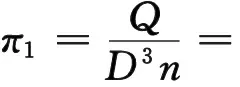
(3)

(4)

(5)

式(3)、(4)和(5)式中，ϕ表示泵的比流量，Re表示泵的雷诺数，ν表示输送介质的运动粘度，ψ表示泵的比扬程。在微型离心泵输送单相介质的情况下，原型泵和模型泵只需要满足π1，π2，π3为同一常数，则可以认为原型泵和模型泵相似。

2.2 微型离心泵输送粘性介质模化方案设计

采用清水代替血液进行试验研究时，由于血液和水的密度与粘度并不相同(水的密度为998.2 kg/m3，粘度为0.001 Pa·s)，要想模型泵试验结果能够换算成微型离心泵输送血液时的性能，必须要进行模化方案设计，使得原型泵和模型泵相似。

由上述可知，原型泵和模型泵只需要满足π1，π2，π3为同一常数，则可以认为原型泵和模型泵相似，即两台泵在满足几何相似的前提下，还需同时满足比流量、雷诺数和比扬程相等。因此假设，原型泵的特征尺寸为Dp，介质的密度为ρp，介质的粘度为μp，模型泵的特征尺寸为Dm，介质的密度为ρm，介质的粘度为μm。

要保证原型泵和模型泵的雷诺数相等，则原型泵的转速和模型泵的转速需满足式(6)，同时直径满足式(7)。

(6)

(7)

要保证原型泵和模型泵的比流量相等，则原型泵的流量和模型泵的流量需满足式(8)。

(8)

要保证原型泵和模型泵的比扬程相等，则原型泵的扬程和模型泵的扬程需满足式(9)。

(9)

式(6)、式(7)、式(8)和式(9)中，νm表示模型泵的动力粘度，νp表示原型泵的动力粘度，ξ表示为相似系数，取不同的ξ值可以得到不同的模化方案。只有当原型泵和模型泵的直径、转速、流量、扬程同时满足式(6)～(9)时，这两台泵才相似。通过改变相似系数ξ的取值所得到的模化方案如表1所列。为了使输送清水的微型离心泵试验能够有效地展开，需要考虑转速、流量、几何尺寸和扬程等综合因素，从而在众多的模化方案中选择最优方案。

由表1可知，叶轮直径比和流量比随着相似系数ξ的增加而不断降低，转速比和扬程比随着相似系数ξ的增加而不断增加。当相似系数ξ位于区间[-0.5，0.5]内时，转速比、叶轮直径比、流量比和扬程比的差值都较小，模型泵的转速、流量、叶轮直径和扬程可能同时达到一个合理值。因此，可从相似系数ξ位于[-0.5，0.5]的区间内的模化方案中选择最优模化方案。

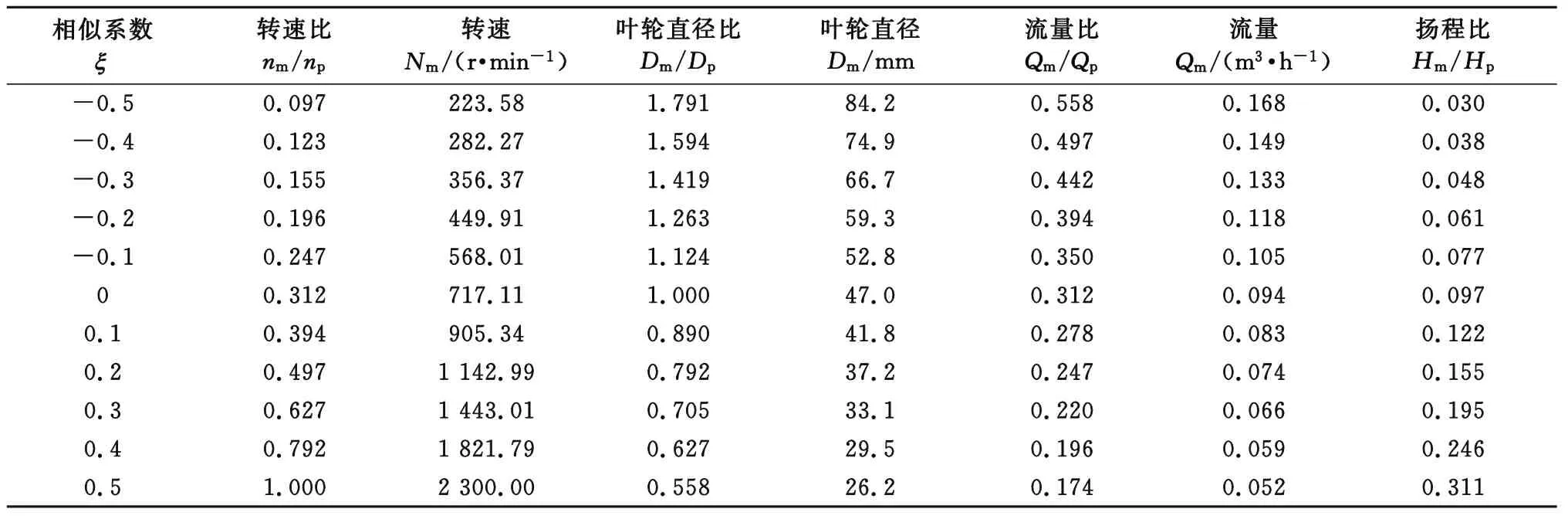
表1 模化方案

3 微型离心泵模化试验方法定常数值模拟研究

3.1 微型离心泵定常数值模拟计算方法

微型离心泵数值模拟中采用定常和非定常计算，均选用SSTk-ω湍流模型，由于模拟介质均为不可压缩流体，因此采用速度进口，出口采用出口自由流(outflow)，壁面采用无滑移边界条件，近壁区域采用标准壁面函数。

3.2 不同模化方案下的数值模拟结果分析

对原型泵输送血液时的情况以及相似系数ξ为-0.5、-0.2、0、0.2和0.5时的模化方案进行数值模拟，在选择最优模化方案的同时，验证相似理论和模化方案的正确性。清水代替血液的模化结果见表2。由表2可知，通过对相似系数ξ为-0.5、-0.2、0、0.2和0.5的模化方案进行数值模拟所得扬程比，与根据相似理论得到的扬程比几乎相同，不同相似工况下的原型泵和模型泵的效率也几乎相同，表明上述通过相似准则得到的模化方案是正确的。完全可以通过采用清水作为试验介质来代替血液进行试验。当相似系数ξ为-0.5和-0.2时，位于区间[-0.5，0]内，扬程太小，影响测量精度。当系数ξ为0.2和0.5时，位于区间[0，0.5]内，扬程满足要求，但是叶轮直径太小，加工难度大。因此当系数ξ为0时，为最优模化方案。

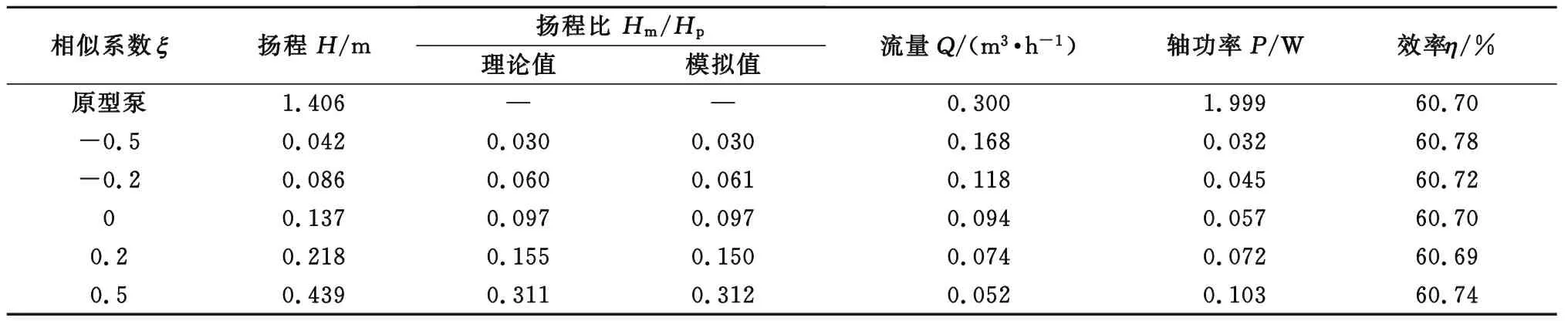
表2 清水代替血液的模化结果

4 微型离心泵非定常数值模拟研究

4.1 微型离心泵非定常数值模拟计算方法

为了获得更快的收敛速度，将定常求解的结果作为非定常解的初始条件。非定常计算中的原型泵时间步长设置为7.246×10-5s，模型泵时间步长设置为2.324×10-4s，即原型泵和模型泵叶轮分别旋转1°所需的时间，时间步设置为1 800步，即记录叶轮旋转5圈泵内流动状态。为了比较原型泵和模型泵内流动情况是否相似，在泵内关键位置处设置了监测点，用于监测微型离心泵内部流动随时间的变化情况。原型泵和模型泵内各监测点见表3。

表3 原型泵和模型泵内各监测点位置

4.2 原型泵和模型泵出口压力随时间变化规律

在研究常规尺寸离心泵输送单相介质非定常模拟时，通常通过监测泵的出口压力是否随时间达到周期性波动来判断是否收敛，因此也需要对微型离心泵的出口压力进行监测。由图3和图4可知，原型泵和模型泵的出口压力随时间变化趋势相似，均随时间进行周期性波动。

图3 原型泵出口压力随时间变化曲线

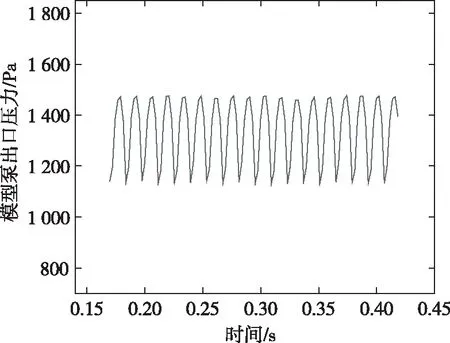
图4 模型泵出口压力随时间变化曲线

为了比较原型泵和模型泵的出口压力随时间变化趋势，绘制原型泵和模型泵出口压力随时间步变化局部放大对比图，如图5所示。由图5可知，原型泵和模型泵的出口压力随时间步变化趋势完全相同，但是对应的压力和时间并不相同。原型泵的出口压力约为模型泵出口压力的10.8倍。由于原型泵和模型泵的转速不同，叶轮旋转5圈的时间也不相同，原型泵叶轮旋转5圈时间是模型泵叶轮旋转5圈时间的0.3倍，也是原型泵和模型泵转速的比值。因此，根据模型泵的出口压力随时间变化规律完全可以推算出原型泵的出口压力随时间变化规律。

图5 原型泵和模型泵出口压力随时间步变化局部放大对比图

4.3 原型泵和模型泵蜗壳Ⅰ-Ⅶ截面上的压力随时间变化规律

由于蜗壳的结构较为复杂，为研究原型泵和模型泵的蜗壳内流动是否相似，在蜗壳的Ⅰ-Ⅶ截面中心位置分别设置了监测点vm1至vm7。由图6和图7可知，原型泵和模型泵蜗壳Ⅰ-Ⅶ截面压力随时间变化趋势相似，监测点vm1至vm7的压力随时间成周期性波动。为了比较原型泵和模型泵蜗壳Ⅰ-Ⅶ截面压力随时间变化趋势，针对监测点vm1和vm7绘制原型泵和模型泵蜗壳截面压力随时间步变化局部放大对比如图8所示。由图8可知，原型泵和模型泵蜗壳Ⅰ-Ⅶ截面压力随时间步变化完全相同，但是对应的压力和时间不同，可以根据模型泵蜗壳Ⅰ-Ⅶ截面随时间变化规律推算出原型泵蜗壳Ⅰ-Ⅶ截面随时间变化规律。由图6、图7和图8可知，监测点vm1的压力波动幅度最大，并且平均压力最大，监测点vm1至vm7上的平均压力是不断下降的。这是由于监测点vm1靠近蜗舌，蜗舌处流动比较复杂，压力波动幅度较大，并且由于微型离心泵的额定工作流量大于设计流量，流经蜗壳Ⅰ-Ⅶ截面的流体流速过高，蜗壳对动能的转化能力较差，压力不断下降。

图6 原型泵蜗壳Ⅰ-Ⅶ截面压力随时间变化曲线

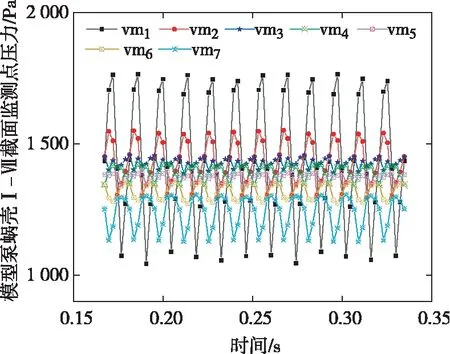
图7 模型泵蜗壳Ⅰ-Ⅶ截面压力随时间变化曲线

图8 原型泵和模型泵监测点vm1和vm7上压力随时间步变化局部放大对比图

4.4 原型泵和模型泵蜗壳第Ⅷ截面压力随时间变化规律

由于从第Ⅷ截面开始蜗壳流道的截面面积突然增大，且离蜗舌较近，因此设置监测点vm8-1至vm8-9监测第Ⅷ截面上的压力随时间的变化规律。

由图9和图10可以看出，原型泵和模型泵蜗壳第Ⅷ截面上各监测点压力随时间变化趋势相似，各监测点上压力都随时间周期性波动。由图可知监测点vm8-2的平均压力最高，监测点vm8-1平均压力略低于监测点vm8-2，并且监测点vm8-2至vm8-9的平均压力是不断下降的，监测点vm8-9的平均压力最低，且下降幅度最大。这是由于蜗壳第Ⅷ截面面积突然增大，从叶轮流出的流体不易受蜗壳作用产生周向运动，监测点vm8-1靠近叶轮，受叶轮旋转带动作用进行周向运动，监测点vm8-2至vm8-9逐渐远离叶轮，受叶轮扰动作用逐渐减小，因此产生了监测点vm8-1平均压力略低于监测点vm8-2，监测点vm8-2至vm8-9的平均压力不断下降的现象。而监测点vm8-9距离叶轮最远且最接近蜗壳壁面，受蜗壳作用影响产生周向运动，压力进一步下降。

图9 原型泵蜗壳第Ⅷ截面上压力随时间变化曲线

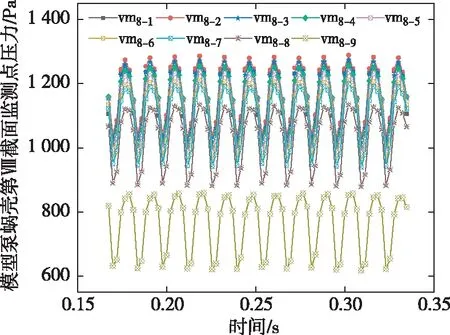
图10 模型泵蜗壳第Ⅷ截面上压力随时间变化曲线

为了比较原型泵和模型泵第Ⅷ截面处压力随时间变化是否完全相似，选取监测点vm8-1和vm8-9绘制压力随时间步变化局部放大对比如图11所示，结果表明原型泵和模型泵蜗壳第Ⅷ截面压力随时间步变化完全相同，但是对应的压力和时间不同，可以根据模型泵蜗壳第Ⅷ截面压力随时间变化规律推算出原型泵第Ⅷ截面压力随时间变化规律。

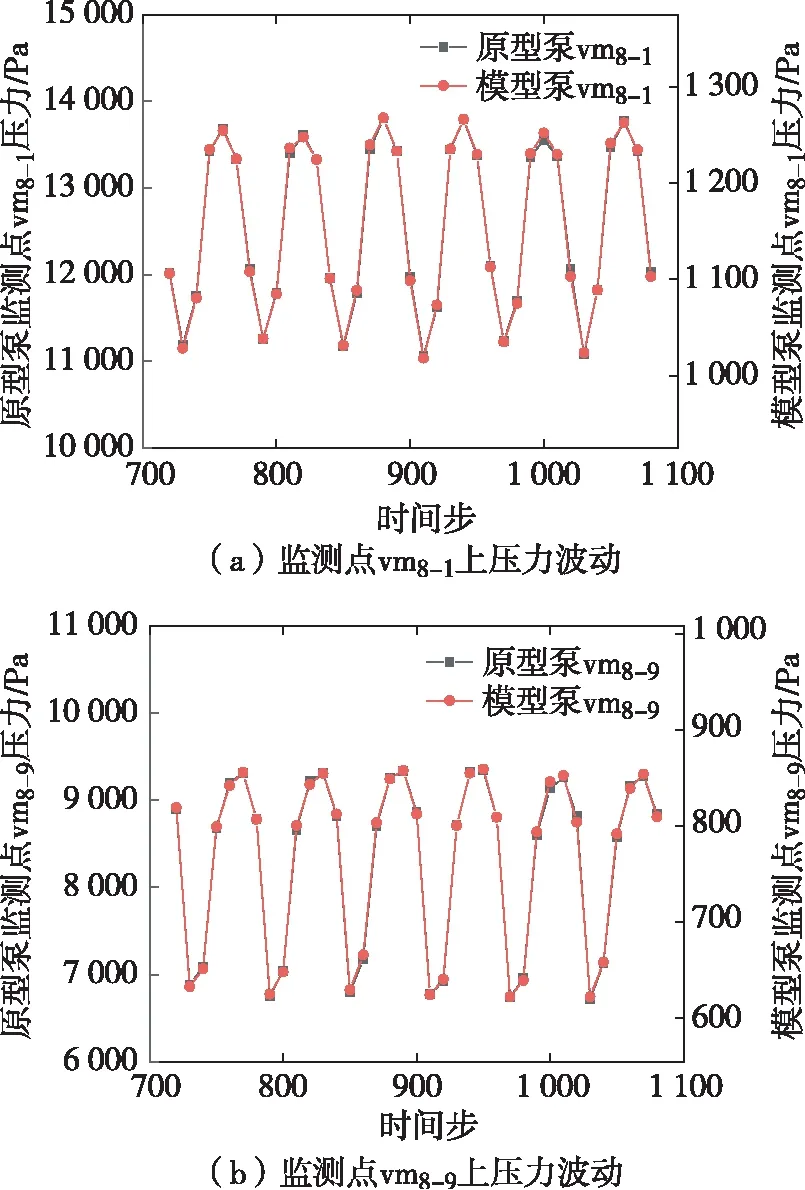
图11 原型泵和模型泵监测点vm8-1和vm8-9上压力随时间步变化局部放大对比图

4.5 原型泵和模型泵不同时刻泵中截面上压力分布

为研究原型泵和模型泵不同时刻泵内截面上压力分布，选取同一周期内原型泵和模型泵中截面上不同时刻压力分布，如图12和图13所示。由图12和图13可知，原型泵和模型泵在不同时刻下的泵内压力云图分布规律相同，但是压力大小并不相等。不论叶片和蜗舌夹角如何变化，原型泵和模型泵的泵内压力都随着叶轮半径的增加而增加，蜗壳第Ⅰ截面至第Ⅶ截面压力普遍较高，由于蜗壳第Ⅷ截面至第Ⅸ截面间面积突然增大，因此第Ⅷ截面处压力较低。随着叶片和蜗舌夹角增大时，第Ⅰ截面靠近蜗舌区域，压力变化较为明显。受叶轮与蜗壳间的动静干涉的影响，蜗壳区域压力变化较大，叶轮区域压力变化较小。

图12 原型泵中截面上不同时刻压力分布

图13 模型泵中截面上不同时刻压力分布

4.6 原型泵和模型泵蜗壳Ⅰ-Ⅶ截面上的速度随时间变化规律

为了研究原型泵和模型泵内部流动是否相似，在上述压力相似分析的基础上，本节开始进一步研究泵内速度是否相似。对原型泵和模型泵蜗壳Ⅰ-Ⅶ截面上的速度随时间变化进行监测，如图14和图15。由图14和图15可知，原型泵和模型泵蜗壳Ⅰ-Ⅶ截面上的速度随时间变化规律相似，均随时间周期性波动。对应位置上原型泵的速度约为模型泵的3.18倍。监测点vm1靠近蜗舌，由于流体流速过高，对蜗舌产生冲击，在蜗舌处产生流动分离现象，形成低速区，因此监测点vm1速度最低，波动幅度最大，并且流体经叶轮进入蜗壳时，流速过高，在蜗壳内产生多个高速区，部分监测点在高速区内，从而形成了监测点vm2至vm7速度忽高忽低的现象。

图14 原型泵蜗壳Ⅰ-Ⅶ截面速度随时间变化曲线

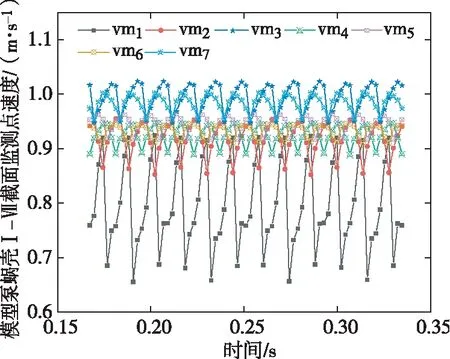
图15 模型泵蜗壳Ⅰ-Ⅶ截面上速度随时间变化曲线

4.7 原型泵和模型泵蜗壳第Ⅷ截面速度随时间变化规律

原型泵和模型泵蜗壳第Ⅷ截面上的速度随时间变化如图16和图17所示。由图16和图17可知，原型泵和模型泵蜗壳第Ⅷ截面上的速度随时间变化规律相似，均随时间产生周期性波动。由图可知，监测点vm8-1至vm8-9的速度均高于监测点vm1至vm7的速度，且监测点vm8-1速度最大，波动幅度最大，监测点vm8-2至vm8-8的速度忽高忽低，没有规律性可言，而监测点vm8-9的速度又相对较高。这是由于蜗壳第Ⅷ截面面积突然增大，流体经叶轮流出后不易因蜗壳作用变成周向运动，所以流体流速过快，流动不稳定，从而造成监测点vm8-1至vm8-9的速度普遍较高，监测点vm8-2至vm8-8速度忽高忽低的现象，而监测点vm8-1靠近叶轮，受叶轮旋转带动作用，进行周向运动，因此速度最高，波动幅度也最大，监测点vm8-9远离叶轮且靠近蜗壳壁面，因蜗壳作用变成周向运动，流动相对稳定，速度相对较高。

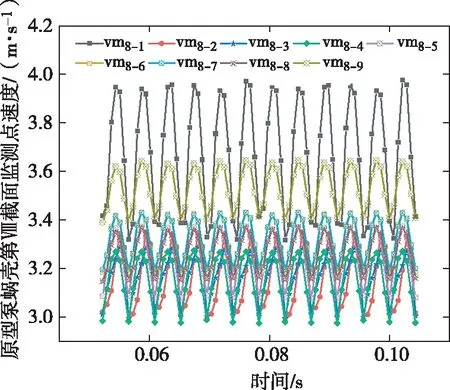
图16 原型泵蜗壳Ⅷ截面上速度随时间变化曲线

图17 模型泵蜗壳Ⅷ截面上速度随时间变化曲线

4.8 原型泵和模型泵不同时刻泵中截面上速度分布

为研究原型泵和模型泵不同时刻泵内截面上速度分布，选取同一周期内原型泵和模型泵截面速度分布，如图18和图19所示。由图18和图19可知，原型泵和模型泵内部速度的分布相似，但速度大小不同。不论叶片和蜗舌的夹角如何变化，原型泵和模型泵的泵内速度均由叶轮进口处至叶轮出口出不断增大，叶轮出口的速度最大，当叶片和蜗舌的夹角变大时，叶轮出口速度的变化也更明显，叶轮进口和蜗壳出口处的速度较小，蜗壳出口处存在一处低速区域。当泵内液体临近第Ⅷ截面处时速度会有所增加，由于微型离心泵的蜗壳在第Ⅷ截面后突然增大，当泵内液体经过第Ⅷ截面后，速度开始降低。受叶轮出口速度的影响，从第Ⅷ截面往后，蜗壳外侧速度较大。

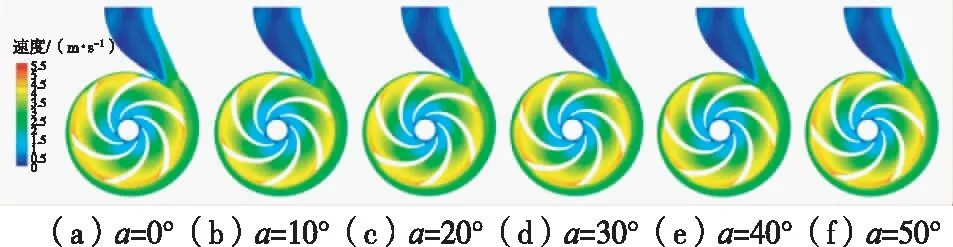
图18 原型泵截面上速度分布

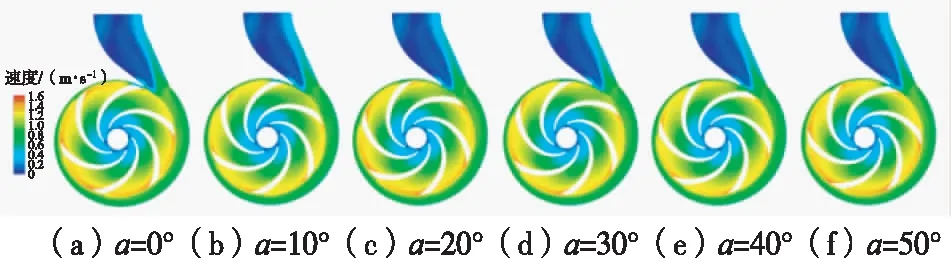
图19 模型泵截面上速度分布

由原型泵和模型泵的内部流动状态分析可知，原型泵和模型泵内的流动是相似的，根据模型泵内的流动可以换算得到原型泵内的流动情况。进一步验证了相似理论和模化方案的正确性，表明采用清水代替血液进行模化试验是可行的。

5 结语

(1)根据π定理，建立了微型离心泵输送单相介质的相似准则，推导出原型泵和模型泵的相似关系，根据相似关系设计模化方案，选择最优方案时，需要考虑转速、流量、几何尺寸和扬程等综合因素。

(2)数值模拟的结果与相似理论所得结果完全一致，表明上述通过相似准则得到的模化方案是正确的，完全可以通过采用清水作为试验介质来代替血液进行试验。

(3)原型泵和模型泵的压力随时间变化规律完全相同，虽然压力和速度大小不同，但是对应位置上原型泵的压力约为模型泵的10.8倍，原型泵的速度约为模型泵的3.8倍，原型泵叶轮旋转5圈时间是模型泵叶轮旋转5圈时间的0.3倍。根据模型泵的压力(速度)随时间变化规律完全可以推算出原型泵的压力(速度)随时间变化规律。

(4)原型泵和模型泵在不同时刻下的压力分布云图和速度分布云图相似，表明原型泵和模型泵的内部流动相似，根据模型泵内的流动可以换算得到原型泵内的流动情况，进一步验证了相似理论和模化方案的正确性，表明采用清水代替血液进行模化试验是可行的。