基于MSST的高压直流线路故障定位方法

郑茂然，陈朝晖，余江，李正红，杨涛，高湛军

(1. 中国南方电网有限责任公司，广州510663；2. 山东大学 电网智能化调度与控制教育部重点实验室，济南250061)

0 引言

随着半导体技术的发展，柔性直流输电技术(VSC-HVDC)应运而生，由于其不存在换流失败现象、无需滤波器与功率补偿设备和易于扩展及模块化等优点[1 - 2]，在直流输电领域拥有广阔的前景[3 - 4]。但是由于直流输电线路多分布于恶劣的环境中且跨越距离很长[5]，直流线路故障概率在高压直流输电系统故障中占比较高，约占50%[6 - 7]，提高直流输电线路故障测距的精度，缩小测距误差，对清除线路故障，缩短故障检修时间，提高供电可靠性具有重要意义。

目前高压直流输电线路的故障定位方法仍广泛使用行波法[8]。针对行波法的主要误差由波速造成的问题，国内外学者提出很多解决办法。一类方法为采集多个波头信息，在公式中利用冗余信息消除波速的影响。文献[9 - 10]通过在线路增加测点的方式，推导不含有波速的故障定位公式，消除波速对定位误差的影响。文献[11]通过极性识别多次波头到达时刻，利用双端测距原理计算故障距离，消除波速的影响。文献[12 - 13]同样采用采集多次波头信息的方式，利用单端测距原理在公式中消除波速，减小定位误差。

另一类方法是根据行波的传播特性，精确每个波头到达时刻对应的波速。文献[14 - 15]提出了考虑波速频变特性的定位方法，与普通行波法相比，该方法不仅需要确定波头到达测点的时刻，还需要确定该时刻对应的频率，进一步确定其对应的波速，最关键的问题仍是波头的识别与标定。目前解决该问题的最主要的方法有导数法、小波变换、数学形态学和希尔伯特-黄变换及其改进算法[16 - 20]。为实现波速和行波到达时刻的统一，文献[21]将行波波速拟合为故障距离的函数，文献[22]分析了行波波速和行波频率的关系，采用改进的希尔伯特黄变换识别行波频率和到达时间，进而确定该时刻到达测量点行波的传播速度。文献[23 - 24]采用变分模态分解和同步挤压小波变换(variational mode decomposition and syncrosqueezing wavelet transform, VMD-SWT)联合方法对信号进行时频分析，确定波头到达时刻及对应波速。以上方法在考虑波速变化后，定位精度得到显著提高。

在考虑行波频变特性的定位方法中，提高时频特征的识别精度是关键。本文采用多重同步压缩变换(multisynchrosqueezing transform, MSST)对信号进行时频分析，得到精确的频率和对应时间，最后根据频率确定波速实现故障定位。首先将采集到的两端电压信息解耦得到其线模分量，然后通过MSST提取突变点的时频特征，在确定波速与波头到达时刻之后利用计及波速频变特性的两端测距公式计算故障距离。由于MSST的挤压特性，频率识别精度更高，定位精度更高，具有较好的耐过渡电阻能力。

1 多重同步压缩变换(MSST)原理

MSST是由Yu Gang等[25]在2019年提出的一种新的提取信号时频特征的方法，其原理是对经过短时傅里叶变换(short-time Fourier transform, STFT)的信号进行多次的同步压缩处理，极大地提高了信号在时域与频域的聚集程度。并且针对进行多次同步压缩处理导致的计算量大、时间长等问题，通过迭代方式优化了算法流程。

信号y(x)的STFT定义为G(t,ω)：

(1)

式中：g(·)为时间窗函数；x为原信号的时间跨度；t为在时间轴上平移的距离；ω为瞬时频率。由于故障分量包含多种频率分量，为抑制频域分量能量泄露为后续多重挤压提供准确的信号，即要求窗函数旁瓣窄并且衰减速度慢，综合上述要求选用Hamming窗。

以简单的单分量信号为例，信号如式(2)所示：

y(x)=A(x)ejφ(x)

(2)

式中：A(x)为信号幅值；φ(x)为信号相位。

在一个短时间窗x∈[t-Δt，t+Δt]内，假设∃ε足够小，对于∀t,|A′(t)|≤ε,|φ″(t)|≤ε， 信号y(x)可认为是在此短时间窗内的纯谐波信号。

对于时间窗长度的选择，在MATLAB中数据窗长度选择采样点数的1/4，但此时数据的采样点数为2的次方，而本文采样点数为6 000，因此选择最接近6 000的2的12次方数4 096的1/4，考虑MSST会在频率方向对STFT结果进行挤压，因此在STFT处理中选择较高的时间分辨率，牺牲一定的频率分辨率，本文的时间窗最终长度选择500个采样点，即为0.5 ms。

根据泰勒级数展开，信号的幅值函数和相位函数可以分别表示为

A(x)=A(t)

(3)

φ(x)=φ(t)+φ′(t)(x-t)

(4)

将式(3)和式(4)带入式(2)，信号y(x)可表示为

y(x)=A(t)ej[φ(t)+φ′(t)(x-t)]

(5)

于是，式(1)可以改写为

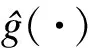
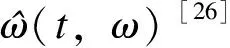
(8)

在得到信号的瞬时频率估计值后，对经过STFT处理得到的G(t,ω)进行同步压缩变换(SST)，SST采用频率重分配因子Ts(t,η)来完成对时频的聚集，利用狄拉克δ函数δ( )完成瞬时频率的估计值对理想频率η的聚集[27 - 28]，其表示为

(9)

对于多分量信号(以两分量叠加的信号为例)

y(x)=A1ejφ1(x)+A2ejφ2(x)

(10)

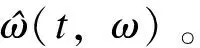
(12)

由于时间窗函数g(·)的范围为[t-Δt，t+Δt]，对于其傅里叶变换可以得到

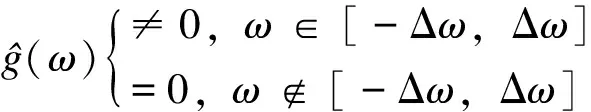
(13)

假设两分量之间有足够距离可以被分离，即

φ′1(t)-φ′2(t)>2Δω

(14)

(15)

将式(15)代入公式(9)可得多分量信号的SST表达式如式(16)所示。

其中

式中：k=1,2,3,…,n， 代表多分量信号的第k个分量；Gk(t,ω)、Ak、φk分别为第k个分量的STFT结果、幅值与相位。

以故障发生在100 km，过渡电阻300 Ω为例，图1为对两端测量装置采集的线模分量经过SST处理后的时频关系。

图1 SST处理后的行波时频关系Fig.1 Time-frequency relationship of traveling wave after SST

根据图1经过SST得到的时频关系计算得到的故障距离为97.289 km，所得故障距离明显错误，其原因是故障行波分量中各种频率分量混叠，仅靠一次同步挤压变换无法准确提取其时频特性。

为获得更高精度的时频特性，对得到的时频谱继续进行SST处理，经过N重处理后，可得到：

(18)

当过渡电阻增大时，采集得的行波幅值会降低，由式(6)、(16)、(18)可以看出经过SST后的时频关系函数的幅值也会变小，但是突变时刻的时频关系相较于其他时刻仍很明显，对时频关系的提取影响较小。由于行波的色散特性，当故障距离变化时，故障点距离采集装置越远行波的衰减越严重，各种频率分量的混叠越难以识别，会对行波时频特征的提取造成困难，由于MSST抑制了频域能量的泄露并在频域方向提高了行波的时域聚集程度，减小了由行波衰减造成的误差。

在对信号进行MSST处理前先用连续小波变换(continuous wavelet transform,CWT)对行波信号预处理，确定MSST的分解层数。经过CWT得到的小波量图如图2所示。由图2可以看出整流侧和逆变侧的瞬时频率主要集中在5个频率区间，因此对信号的MSST处理重数可以选择5重，经过5重MSST处理后的行波时频关系如图3所示。

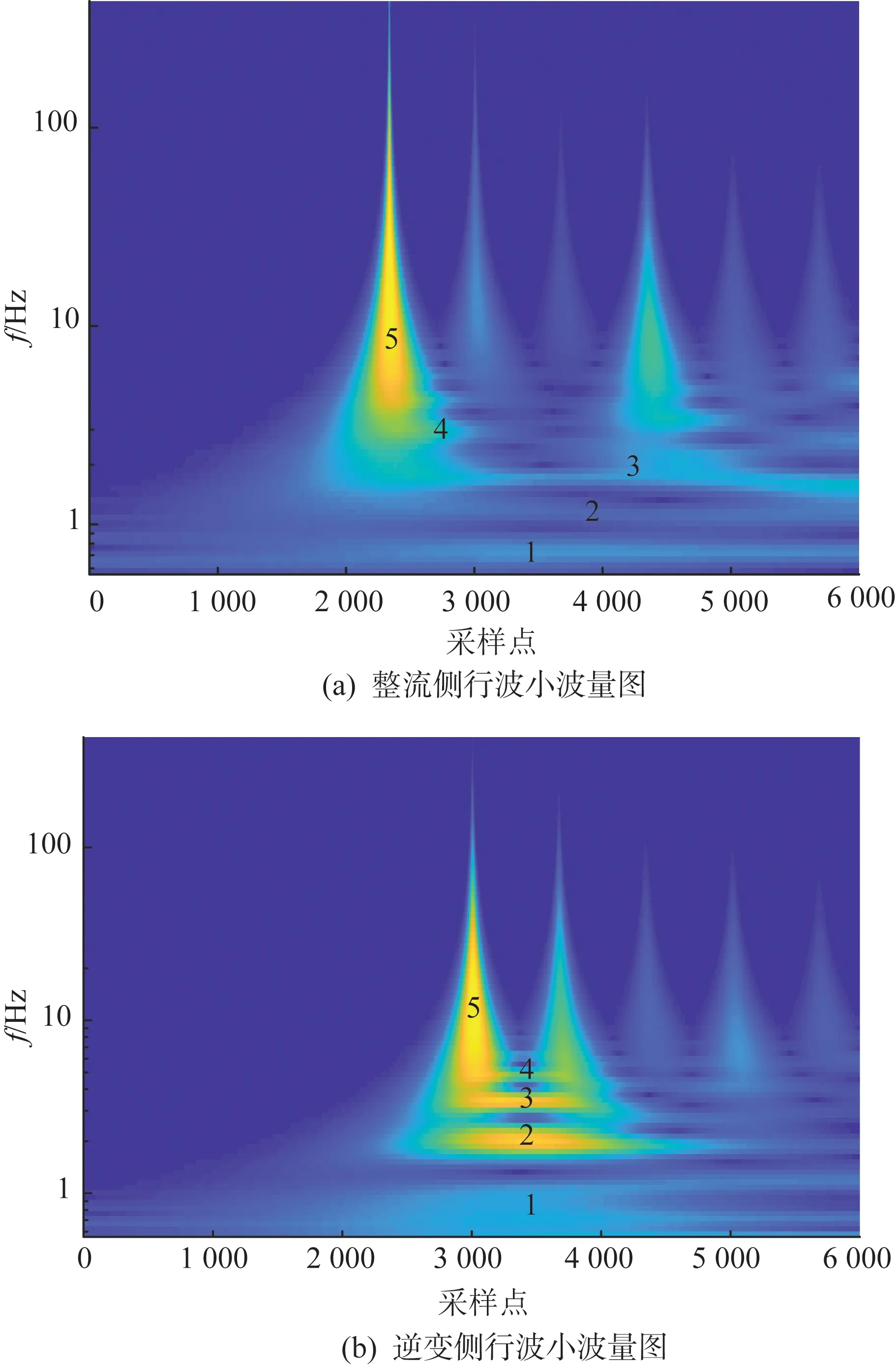
图2 行波小波量图Fig.2 Wavelet scalogram of traveling wave

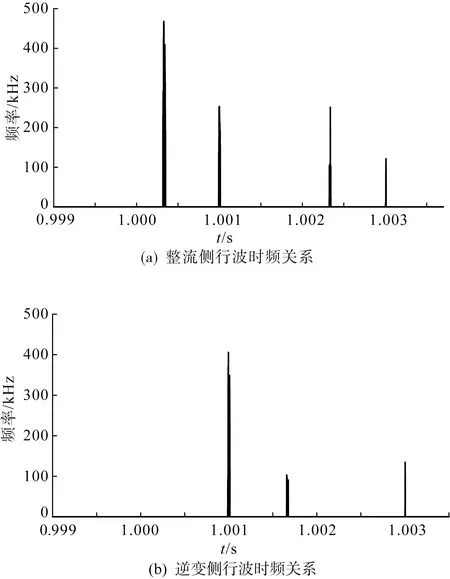
图3 MSST处理后行波时频关系Fig.3 Time-frequency relationship of traveling wave after MSST

2 基于波速频变特性的故障测距原理

如图4所示，采用双端测距，行波采集装置分别安装在线路两端，即A、B两处。假设故障发生在t0时刻，故障点记为F，在A端采集装置处采集到的行波分量其波头到达时间为tA，该时刻对应的波头频率为fA；在B端采集装置处采集到的行波分量其波头到达时间为tB，该时刻对应的波头频率为fB；频率为fA的行波波速度为vA(fA)，频率为fB的行波波速度为vB(fB)。

图4 行波传播示意图Fig.4 Schematic diagram of traveling wave propagation

根据故障距离与行波波速和时间的关系可得故障点距整流侧的距离XA为：

XA=vA(fA)(tA-t0)

(19)

故障点距逆变侧的距离XB为：

XB=vB(fB)(tB-t0)

(20)

此外，线路总长度L为：

L=XA+XB

(21)

将上述3式联立，消去故障发生时刻t0，可得故障点距整流侧测量点的距离XA为：

(22)

式中波速vA(fA)、vB(fB)分别为波头到达测量装置时的频率对应的波速。

故障行波某一频率分量的传播速度与频率的函数关系为：

(23)

式中：ω=2πf， 为指定频率分量的角频率；β(ω)为指定频率分量的相位畸变系数，其计算公式为：

(24)

式中：R0、L0、C0、G0分别为输电线路单位长度的电阻、电导、电感、电容。根据上述分析，由式(23)、(24)，可以求得波速度v随频率f变化的曲线，如图5所示。

图5 波速随频率变化的关系曲线Fig.5 The relationship between wave speed and frequency

从图5可以看出，在高频段波速随频率的变化幅度比较大，若用经验波速代替会造成较大误差。由上述分析可以知道，基于波速频变特性的故障定位原理的关键是得到故障行波的时频关系，确定到达测量点的行波频率及对应频率分量到达测量点的时间。因此，准确地提取故障行波的时频特征尤为重要。

3 算法具体实现步骤

根据前述测距原理以及信号的时频分析方法，本文故障测距的流程如图6所示。

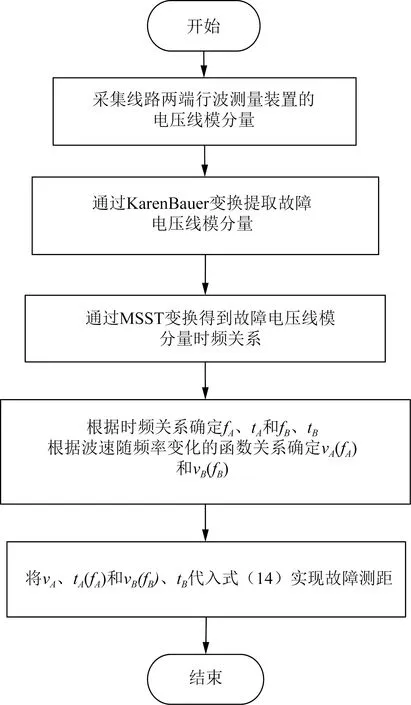
图6 故障测距流程图Fig.6 Flow chart of fault location

1)当线路发生故障时，分别采集整流侧、逆变测的电压行波；

2)利用相模变换矩阵(25)对所采集到的双极电压进行解耦得到其线模分量；

(25)

3)对步骤(2)中所得的两端电压线模分量利用MSST做时频分析，窗口函数选择Hamming窗，窗口长度为0.5 ms，得到如图3所示的信号时频关系，根据时频关系曲线确定其最大值点，该点对应的横坐标即为故障行波到达测量端的时刻，纵坐标为该时刻对应的频率。基于此可获得故障行波到达测量点A、B的时刻tA和tB以及该时刻对应的频率值fA和fB，根据图5中频率和波速的对应关系，确定测量点所检测到行波信号的传播速度vA(fA)和vB(fB)。

4)将故障行波到达测量点的时刻tA和tB以及行波传播速度vA(fA)和vB(fB)带入式(22)，即可计算出故障点距整流侧测量点的距离，实现故障测距。

由图3的时频关系可以得到，故障电压行波到达整流端的时间为1 000.328 1 ms，对应的频率为76 833.333 Hz，对应波速为299.260 9 km/ms；故障电压行波到达整流端的时间为1 000.996 1 ms，对应的频率为81 500 Hz，对应波速为299.290 km/ms。架空线路全长400 km，可以计算得到故障距离为99.957 km，与实际故障距离只相差43 m，测距精度较高。

4 基于实际工程的算例分析

本文根据南方电网某直流线路实际工程为模型在PSCAD中搭建了±500 kV两端MMC模型。该工程采用双极运行方式，线路参数如下：输送容量为3 000 MVA，额定电流3 000 A，线路长度总计390.9 km，输电线路采用架空线，其选用4×JL/LB1A- 720/50铝包钢芯铝绞线，其整流端仿真模型如图7所示。

4.1 不同过渡电阻水平下的定位结果

如图8所示，当故障点过渡电阻变化时，所得电压行波随之变化，过渡电阻越大，所得到的电压行波的幅值随之减小，增大了波头识别的难度，所得到的故障测距误差会略有增大。本文在每个故障点分别设置0、100、200、300 Ω过渡电阻，所得到的故障测距结果如表1所示。

图8 不同过渡电阻行波波形Fig.8 Waveforms of travelling waves with different transition resistances

由表1可以看出，对于在0～300 Ω的过渡电阻，本文所提出的故障定位方法最大误差为0.126 km，最小误差为0.019 km，精度高并有良好的耐受过渡电阻的能力。

表1 故障测距结果Tab.1 Fault location results

4.2 有效性对比

为验证MSST提取行波时频特征的精确度以及采用频变波速对减小定位误差的作用，本文采用经验波速[26]v=296.1 km/s计算故障距离，采用MSST识别波头到达时刻(简称方法一)来证明采用频变波速减小误差的有效性。同时选择同步挤压小波变换(SWT)并利用频变波速计算故障距离(简称方法二)，来对比本文所提方法(简称方法三)识别行波时频特征的优越性。表2为3种方法定位结果的对比，图9为3种方法误差的对比图。

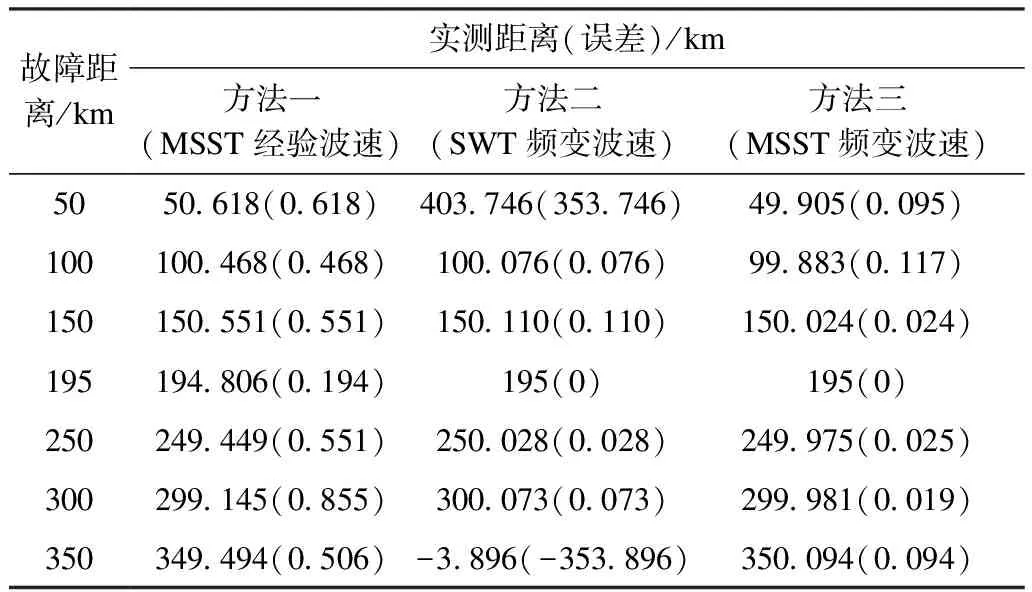
表2 3种方法故障测距结果Tab.2 Fault location results of three methods

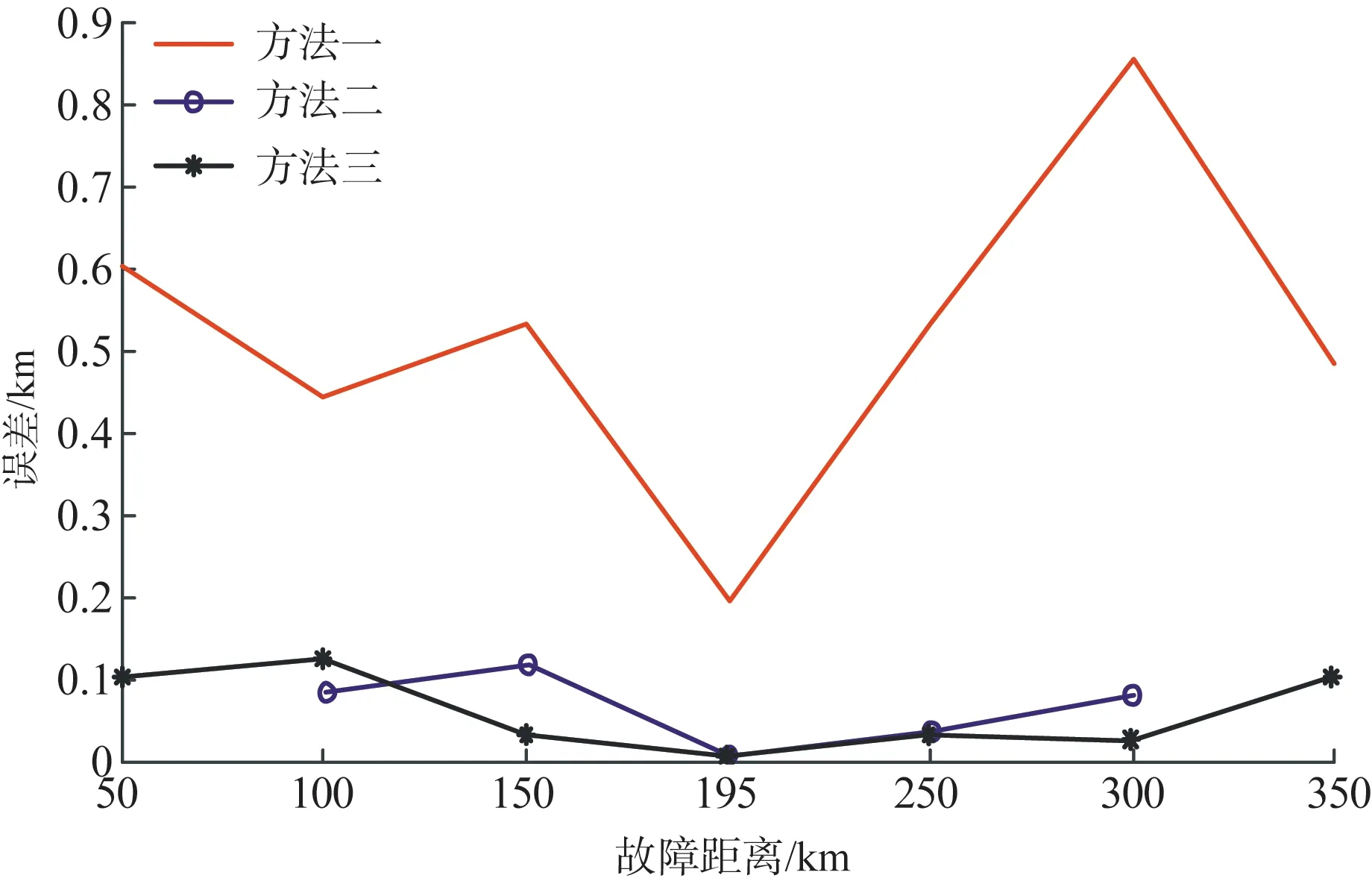
图9 定位误差对比Fig.9 Error comparison of positioning

比较表2与图9中方法一与方法三可以看出，在采用频变波速计算故障距离后，定位的精度有明显的提升，方法一最小误差为231 m，而方法三最大误差为117 m。比较方法二和方法三，图10为两种方法的波头识别精度的对比图。通过表2和图10可以看出两种方法波头识别的精度相差不大，但是当故障发生在距离线路两端较近的时候，所得到的误差较大，甚至出现了明显的错误，如表2中故障发生在50 km与350 km时。从图10可以看出，产生上述误差的原因是通过SWT识别的波头比较平缓，容易识别错误，而MSST不存在此类现象。

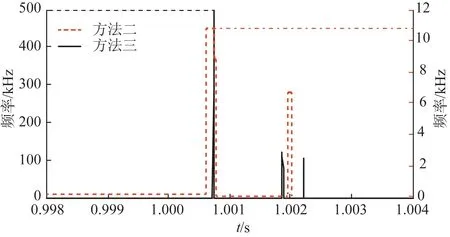
图10 波头识别精度对比Fig.10 Accuracy comparison of wave head recognition

4.3 现场测距结果对比

以该工程发生的3次故障为例，其故障类型均为正极单极短路故障，故障原因为风偏树木导致线路故障，实际的故障距离分别为226.42 km、225.83 km、221.33 km。根据实际录波数据，表3为现场测距结果与本文所提方法所得故障距离的对比。

表3 故障测距结果对比Tab.3 Comparison of fault location results

通过对比可以看出，本文所用方法的定位结果相较于现场定位结果绝对误差提升约0.1 km，相对误差提升约0.026%。

取另一直流工程两次故障，该工程直流线路总长1 223 km，双回架空线运行，总容量6.4 GW。两次故障发生在该工程甲直流线路，故障类型为单极接地故障，实际故障距离为892.22 km与329.66 km，329.66 km处故障录波数据如图11所示。两次故障测距得到的距离与实际距离误差较大，测距对比结果如表4所示。

图11 两端故障数据录波Fig.11 Recording of two terminal fault data

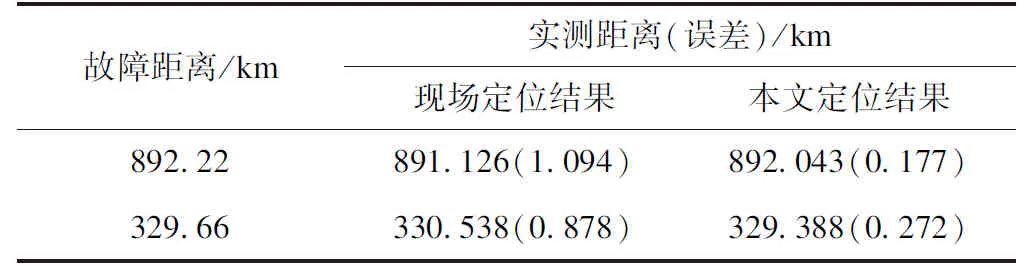
表4 故障测距结果对比Tab.4 Comparison of fault location results

由表4可以看出实际工程中测距结果与实际巡线结果误差均超过了500 m，而用本文提出方法测距误差小于300 m，仍可满足实际工程误差要求。

5 结语

本文提出了基于MSST的高压直流输电线路故障定位方法，分析了计及波速频变特性的故障定位原理，选择MSST对信号做时频分析以提高定位的精准度，最后利用该算法实现MMC-HVDC的故障定位，在各种故障情况下准确度高并且耐受高过渡电阻；经过方法对比后本文所提方法有更高的精度和更强的可靠性。本文所用MSST的同步压缩重数由人为设定，后续针对如何在算法实施之前确定最优压缩重数这一问题继续研究解决。