风电-柔直系统次同步振荡的耦合阻抗模型分析
张帆,尹聪琦,袁豪,洪潮,杨雄平,谢小荣
(1. 直流输电技术国家重点实验室(南方电网科学研究院),广州510663; 2. 电力系统及发电设备控制与仿真国家重点实验室(清华大学电机系),北京100084; 3. 中国南方电网有限责任公司,广州510663)
0 引言
风电机组经柔性直流输电系统(风电-柔直系统)在某些运行工况下会产生次同步频率的振荡现象,严重影响了系统的稳定运行[1 - 3]。近几年,在德国北海Borwin1海上风电-柔直系统[4]、广东南澳风电-柔直系统[5]、上海南汇风电-柔直系统[6]等工程调试或者运行阶段中都曾观测到此类振荡现象。振荡现象严重时会引起柔直单元闭锁、变压器损毁等严重后果。
此类振荡问题多与风电机组控制器及柔直变流器之间的动态相互作用有关[7 - 8]。目前判断其稳定性的方法主要为时域仿真法和频域阻抗分析法。时域仿真法通过仿真软件或者实时数字仿真器(real time digital simulator, RTDS)建立目标系统的详细电磁暂态模型来判断互联系统的稳定性。该方法能够直观地了解系统的稳定状态,提供诸如振荡频率、幅值等信息,但是难以获取振荡的产生机理及影响振荡的关键因素等信息[9]。频域阻抗分析法通过风电-柔直系统的阻抗特性确定系统稳定性[10 - 11],该方法能够直接表示系统在各频段的阻抗特性,物理意义明确,有利于快速确定风电-柔直系统谐振频率处的稳定性及影响谐振频率的关键因素,但是稳定性判断的结果对所建立的阻抗模型的精确程度要求较高,能否精确反应风电-柔直系统在各频段的阻抗特性会直接影响稳定性判断的结果是否正确[12]。风电机组控制器和柔直换流站控制器中的各控制环节会引起系统频率耦合的阻抗特性[13],频率耦合特性主要体现在:当系统某相电流中存在任意fs频率的谐波时,对应会出现2f1-fs频率的谐波(f1为基波频率)。两者在次同步及二倍频频段耦合效应明显,因此当考虑风电-柔直系统在该频段的稳定性时,不可忽略两者的耦合阻抗特性[14]。
本文首先介绍了一种典型风电-柔直系统的拓扑结构,提出了风电及柔直系统阻抗模型的耦合特性;其次,分析了风电-柔直系统阻抗的耦合特性对次同步频段稳定性的影响;然后,基于风电-柔直系统聚合阻抗矩阵行列式,分析了风电机组台数、交流线路长度、风电机组出力程度、柔直控制器参数对风电-柔直系统次同步振荡稳定性的影响;最后,总结了风电-柔直系统阻抗耦合特性及风电机组运行状态对系统稳定性的影响。
1 风电-柔直系统耦合阻抗模型
1.1 风电柔直互联系统
风电场自身需要开阔的场地来充分利用风能,因此多建造在远离负载中心的偏远地区或海上区域,输电距离最高可达上百千米。目前风电场并网均采用柔直并网技术。图1中为某典型风电-柔直互联系统,风电机组经过35 kV交流线路汇集,然后通过升压变压器后再由525 kV线路输送至柔直换流站整流侧,逆变侧连接交流电网。
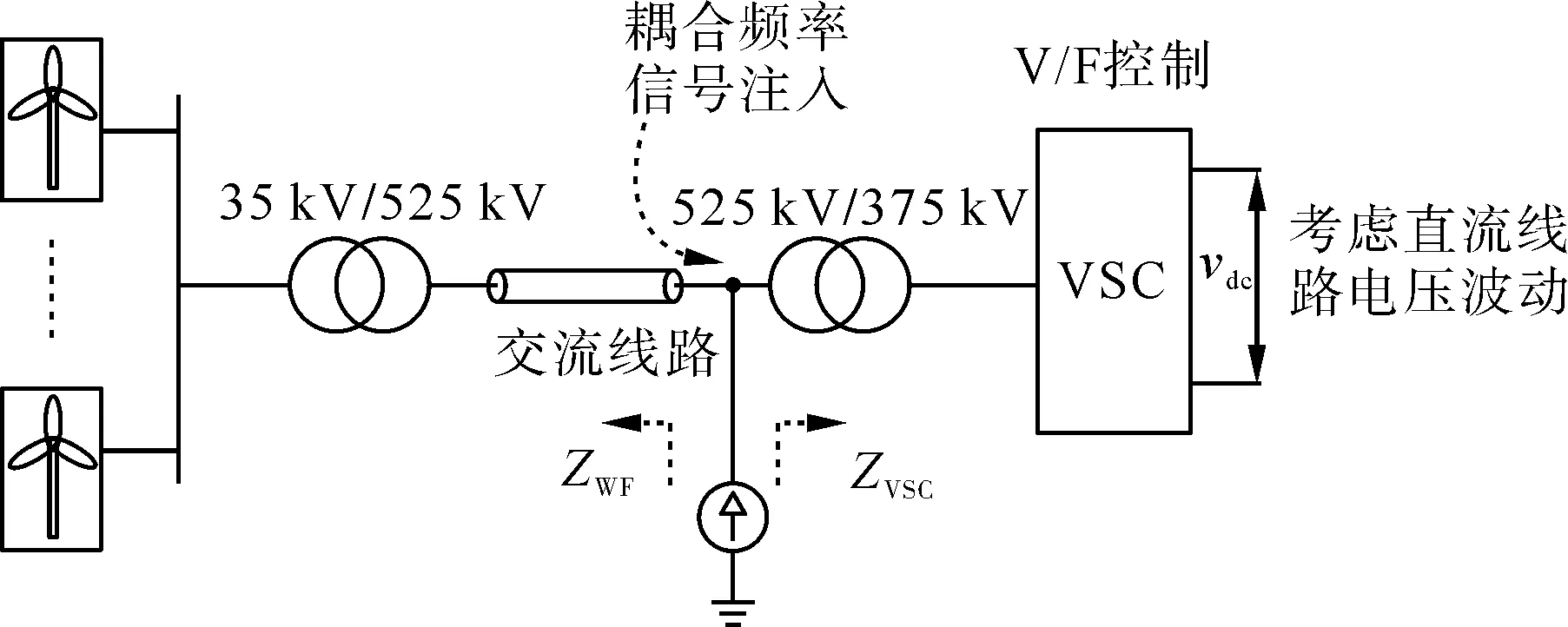
图1 风电-柔直互联系统Fig.1 Interconnected system of wind farm and VSC-HVDC system
1.2 频率耦合效应
假设交流线路上除基波电压分量u1外,还存在次同步频率的小扰动us,则a相电压ua可以表示为:
ua=u1cos(ω1t+φ1)+uscos(ωst+φs)
(1)
式中:ω1和ωs分别为基波电压和小扰动电压的角速度;φ1和φs分别为基波电压和小扰动电压的初始相角。以基于dq轴的控制系统为例,abc/dq变换可以表示为:
(2)
式中θpll为锁相环输出相角。
当交流电压存在小扰动us时,会引起锁相环输出相角波动Δθ,该相角波动同样会引起在该频率下计算得到的小扰动us及其耦合分量,但是其相对于由θpll引起的阻抗耦合特性影响较小,因此在此处省略了Δθ对阻抗特性的影响[15]。将式(1)代入式(2)中,假设小扰动足够小,略去其中高阶谐波分量,可得:
(3)
式中:ud为包含小扰动的d轴电压分量;uq为包含小扰动的q轴电压分量。
根据式(3)可得,当a相电压中包含小扰动时,会分别在d轴、q轴上产生频率为ωs-ω1的扰动电压;与abc/dq变换的推导过程类似,在经过abc/dq逆变换后,dq轴上的频率为ωs-ω1的扰动电压又会在a相电压上分别产生ωs-ω1和2ω1-ωs的电压谐波分量。因此,当系统存在频率为ωs的小扰动时,会同时在交流线路中产生频率为ωs和2ω1-ωs的谐波分量。
1.3 耦合阻抗模型的辨识方法
阻抗模型可采用解析推导法和频率扫描法得到。解析推导法根据风电-柔直系统结构、控制器参数来推导其耦合阻抗模型的难度较大,尤其是当风电-柔直系统线路复杂、风电机组结构差异较大时,推导难度成倍增长。此外,出于保密要求,风电机组及柔直控制器厂家往往不愿公开其参数,进一步加大了从解析式推导系统耦合阻抗模型的难度。
频率扫描法通过在测量点注入频率耦合的小信号电压或电流,通过测量对应频率处的电流或电压幅值,即可计算出该频率处的耦合阻抗特性。依次改变注入的小信号频率,即可获得测量点各频段的耦合阻抗特性。频率扫描法对风电-柔直系统的参数无要求,适用于获取各种工况下的风电-柔直系统的耦合阻抗特性,可以构建风电-柔直系统的阻抗模型,如图2所示。风电-柔直系统的耦合阻抗模型可以表示为:
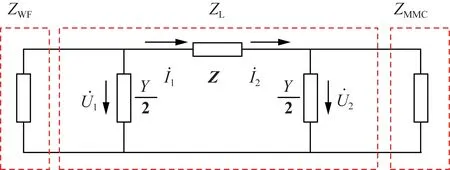
图2 风电场经输电线路接入柔直系统阻抗模型Fig.2 Impedance model of the wind farm connecting into VSC-HVDC system
(4)
式中:ZWF和ZMMC分别为风电场和柔直换流站耦合阻抗模型,其中对角元素下标“ss”、“cc”表示风电-柔直系统在耦合频率的自阻抗特性,既该频率处扰动电压引起的该频率处扰动电流变化;而非对角元素“sc”,“cs”表示风电-柔直系统在耦合频率的互阻抗特性,既该频率处扰动电压引起的耦合频率处扰动电流变化。
2 基于耦合阻抗频率特性的振荡稳定性分析方法
2.1 耦合阻抗模型的聚合
在分别得到风电机组、交流线路及柔直变流器阻抗模型后,得到风电-柔直系统的频率耦合的聚合阻抗矩阵:
Zint=ZWF+ZL+ZMMC
(5)
式中:Zint为频率耦合的聚合阻抗矩阵;ZL为风电场和柔直换流站间的交流线路耦合阻抗模型:
(6)
式中:ZL_ss和ZL_cc分别为交流线路的次同步阻抗特性和超同步阻抗特性,当采用π形线路表示交流线路时,交流线路的阻抗耦合特性可以忽略[16],既认为线路的次同步阻抗特性与超同步阻抗特性一致,既ZL=ZL_ss=ZL_cc。π形线路的次超同步阻抗特性可以表示为:
(7)
式中:r1、x1、g1、b1、l分别为交流线路的单位电阻、单位电抗、单位电导、单位电纳以及线路长度;R、X、G、B分别表示线路的总电阻、总电抗、总电导、总电纳。当分析风电-柔直系统次同步频段的阻抗特性时,π形线路能够满足阻抗分析精度要求。但是当分析风电-柔直系统高频段的阻抗特性时,需要根据精度要求采用多段π形线路阻抗模型、分布式参数线路模型或者频率相关模型[17 - 18]。
风电场、输电线路、柔直变流器的阻抗聚合过程可以分为两部分:1)分别获取风电场、输电线路、柔直变流器的耦合阻抗模型;2)完成风电场接入柔直系统的阻抗聚合。其中风电场、输电线路、柔直变流器的阻抗模型可以通过解析方法建立耦合阻抗模型[19],也可以通过频率扫描法直接获取耦合阻抗模型。耦合阻抗的建模方法主要包括小信号分析法[10]、多谐波线性化法[20]以及状态空间向量法[21],其阻抗模型的推导过程在以往文献中已有详细描述,此处不再赘述,仅给出基于本文耦合阻抗模型所用方法的阻抗特性对比结果。
阻抗聚合形式采用阻抗串并联的方法根据公式(4)—(6),对图1中风电厂经输电线路接入柔直系统进行阻抗聚合,聚合方法如图3所示。
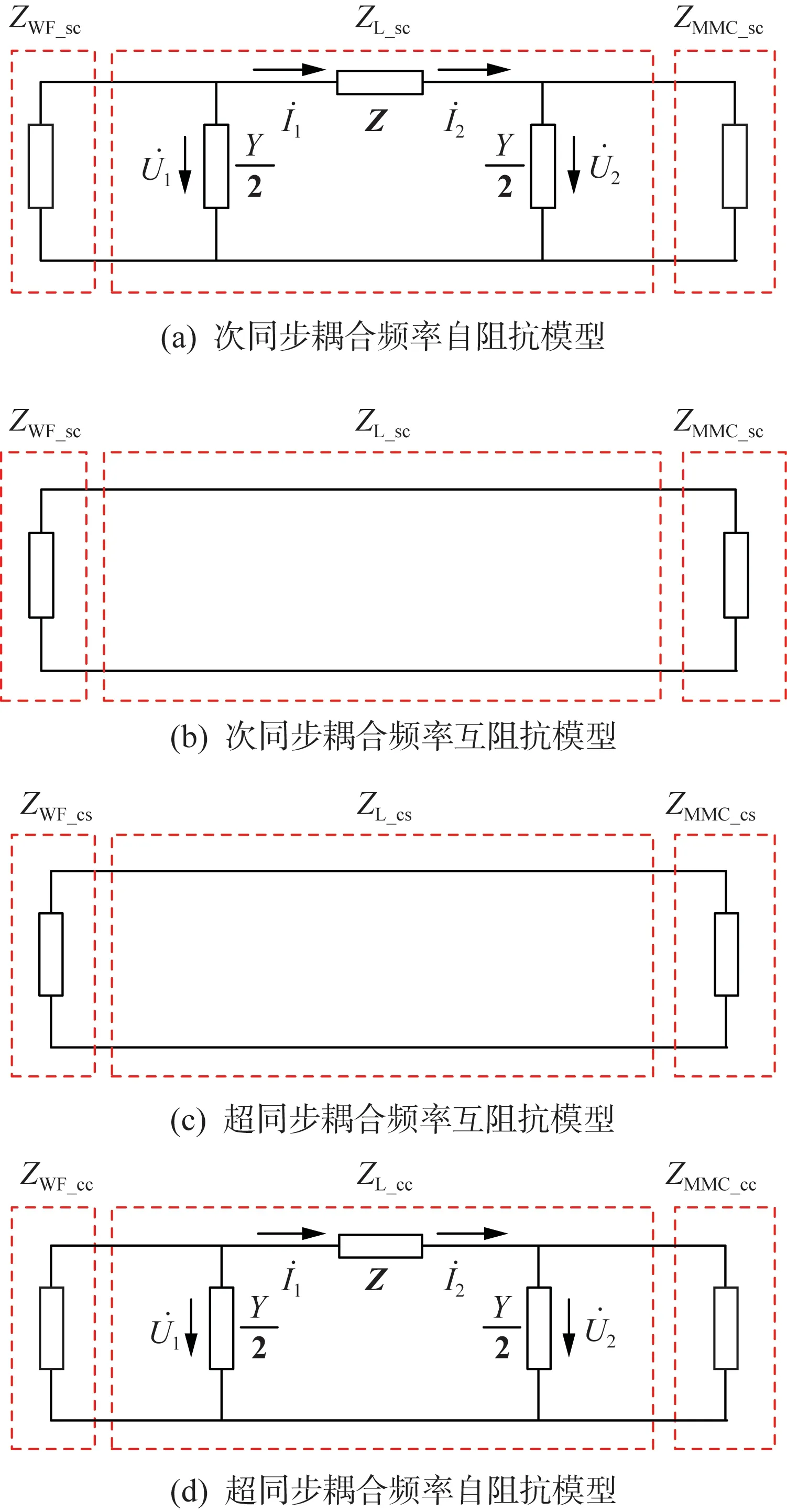
图3 风电场接入柔直系统阻抗聚合方法Fig.3 Impedance aggregating approaches of the wind farm connecting to VSC-HVDC system
由图3可知为风电场接入柔直系统的耦合阻抗的聚合方法,由于风电场、输电线路、柔直变流器阻抗模型的耦合特性已经通过2×2的矩阵进行解耦,因此可以将他们阻抗矩阵的各元素相加,可以得到聚合后的阻抗模型,如式(8)所示。
(8)
2.2 基于聚合阻抗频率特性的稳定性判据
频率耦合的聚合阻抗Zint可以表示为2×2的矩阵形式:
(9)
其行列式可以表示为:
D(Zint)=Zint_ssZint_cc-Zint_scZint_cs=R+jX
(10)
式中R、X分别为聚合阻抗矩阵行列式的实部和虚部。聚合阻抗矩阵行列式D(Zint)的共轭零点会在其等效电抗-频率特性曲线上产生过零点[22]。如果聚合阻抗矩阵行列式D(Zint)等效电抗曲线上存在一个频率为ωssr的过零点,则该系统存在一个频率为ωssr的振荡模式,通过分析该处其等效电阻R(ωssr)与等效电抗斜率Kx(ωssr)之积的正负可判断该振荡模式的稳定性[23]。如果R(ωssr)·Kx(ωssr)>0,表明振荡模式稳定;反之,振荡模式不稳定。即:
(11)
3 算例分析
3.1 算例系统说明
风电-柔直仿真模型结构如图1所示,其中风电场中的风电机组全部由双馈风电机组组成,总容量为300 MW。输出电流经风电场交流线路汇集后经过35 kV/525 kV升压变压器,后经525 kV交流线路输送至柔直换流站。柔直换流站整流侧采用v/f控制。由于直流线路的电压波动会引起柔直整流侧电容电压波动,进而对柔直系统在次同步频段的阻抗特性产生影响,因此需要考虑直流线路的电压波动对柔直变流器阻抗特性的影响[24 - 25]。
3.2 耦合阻抗模型的获取
用频率扫描法获得柔直侧的耦合阻抗模型,当柔直变流器的采用交流电压和无功功率控制模式时其阻抗特性如图4所示。
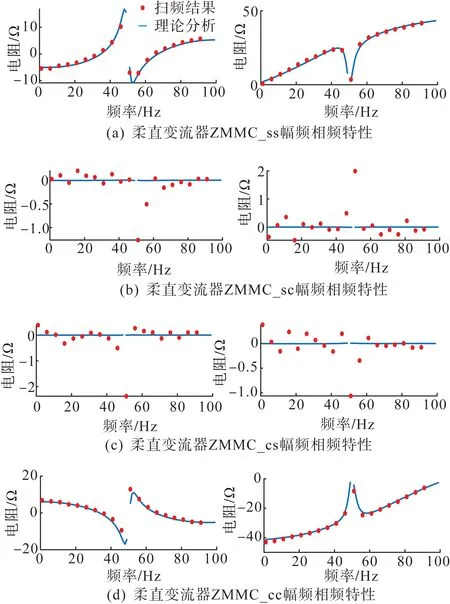
图4 柔直变流器耦合阻抗频率特性Fig.4 Frequency response of the coupled impedance model of the VSC-HVDC system
可见根据扫频得到的柔直变流器的Zss、Zcc阻抗的幅频和相频特性一致,Zsc、Zcs的幅频和相频特性相差较大。初步分析为当柔直变流器采用交流电压和无功功率控制模式时,在Zss、Zcc中的耦合特性较弱,因此Zsc、Zcs相对较小,理论分析结果也显示两者不存在耦合特性,因此可以认为Zsc、Zcs扫频结果和理论分析之间的误差为噪声引起的扰动误差。基于此分析结果可以认为,采用此扫频方法得到的耦合阻抗模型能够满足本算例的次超同步振荡稳定性分析要求。
将频率扫描接入点设置在柔直变流器和输电线路+风电场之间,如图5所示。用频率扫描法获得风电场侧的风电机组加输电线路的耦合阻抗模型,如图6所示。可见在0~20 Hz频段,风电场的自阻抗Zss,Zcc相对较小,随着频率升高,阻抗逐渐增大;同时,自阻抗Zss、Zcc与互阻抗Zsc、Zcs在0~50 Hz频段幅值接近,说明风电场在此频段的耦合特性较强,随着频率增大,耦合特性逐渐减弱。
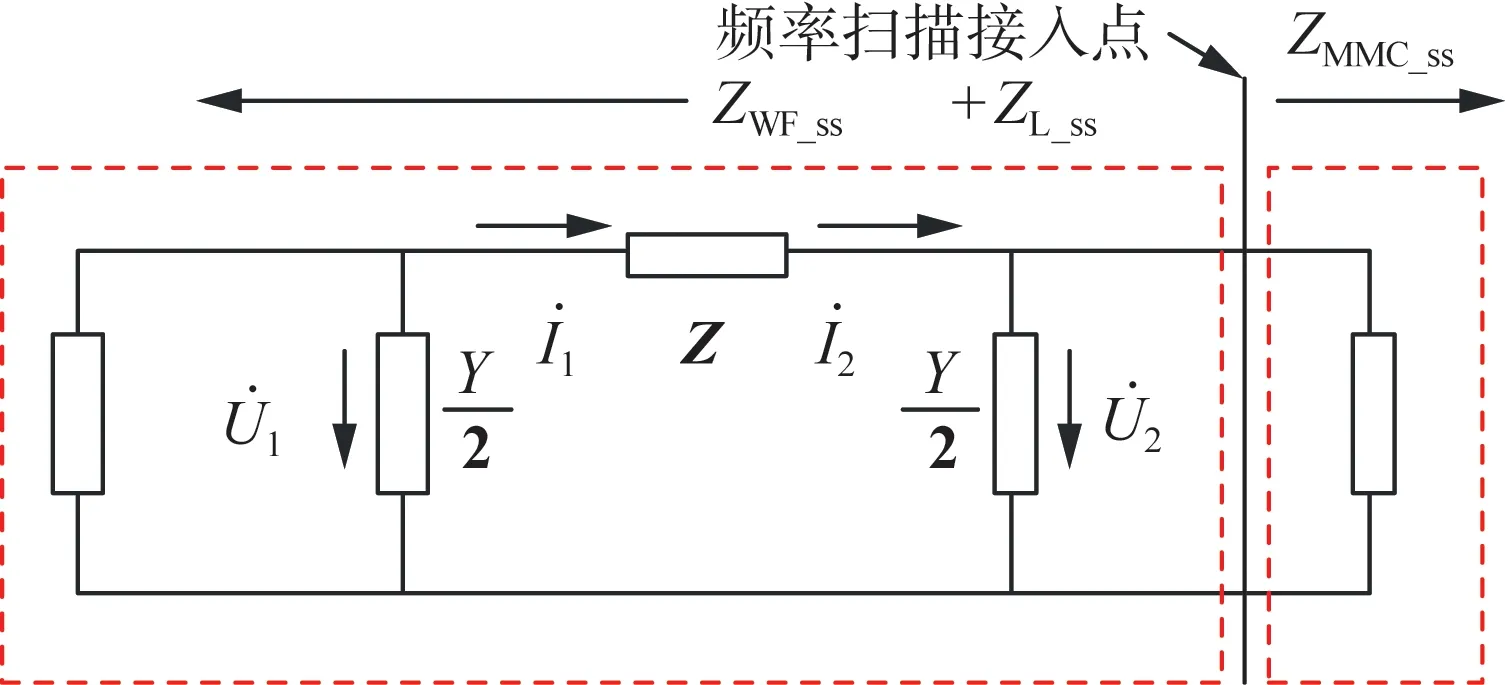
图5 耦合频率扫描方法Fig.5 Frequency scanning approach for the coupled impedance model
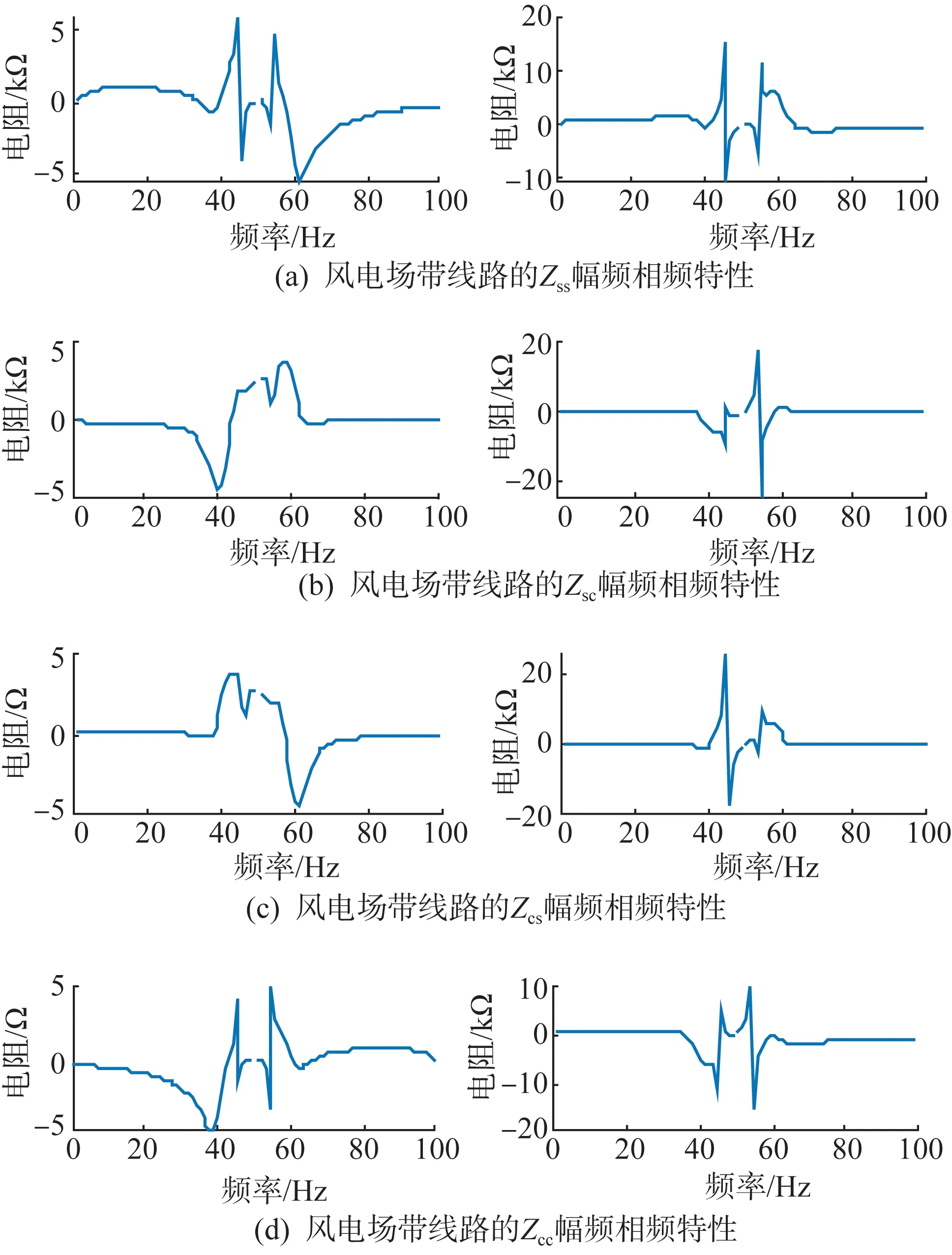
图6 风电场耦合阻抗的频率特性Fig.6 Frequency response of the coupled impedance model of the wind farm
3.3 振荡稳定性分析
基于聚合阻抗频率特性进行振荡稳定性分析,考虑和未考虑频率耦合特性时,聚合阻抗矩阵行列式的频率特性如图7所示,其行列式的过零点如表1所示。当考虑频率耦合特性时,风电-柔直系统的聚合阻抗行列式在7.0 Hz存在过零点,根据式(11)判断,系统在此频率处存在稳定的振荡模式;当未考虑阻抗耦合特性时,风电-柔直的聚合阻抗行列式存在8.2 Hz的过零点,根据式(11)推导该系统在8.2 Hz处应该存在不稳定的谐振点。
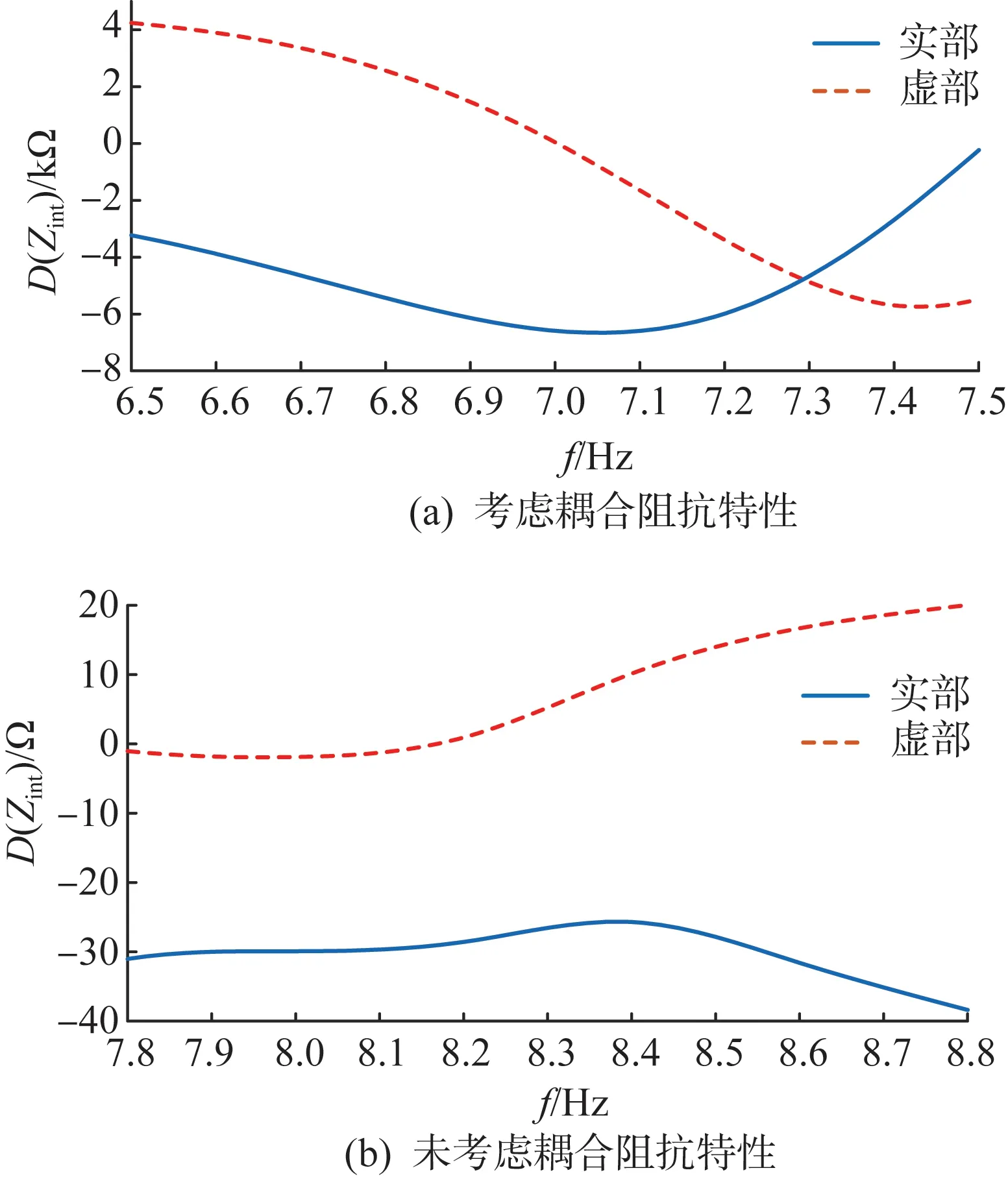
图7 耦合阻抗行列式稳定性判据Fig.7 Stability criteria of the aggregated impedance based on the determinate of the coupled impedance

表1 耦合阻抗谐振点稳定性分析Tab.1 Harmonic point stability of the coupled impedance model
为验证频率耦合阻抗特性对系统稳定性分析结果的影响,在PSCAD仿真软件中搭建了如图1的风电-柔直系统,对理论分析下的工况进行仿真分析。仿真结果显示,在接入点电流中,存在7 Hz的谐波电流,当风电-柔直系统10 s达到稳态后,接入点电流的谐波含量从6.1%逐渐下降,如图8所示。因为谐波含量很小(6%),受到风电机组干扰的影响,在13 s前后会出现谐波上升的情况,但是谐波整体呈现下降趋势,因此判断在系统7 Hz谐振点处稳定。
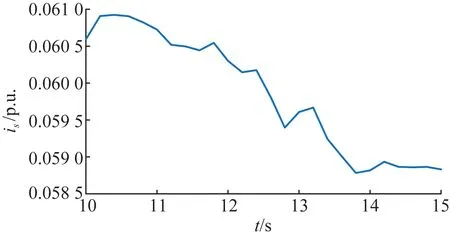
图8 风场与柔直换流站之间的谐波幅值变化Tab.8 Magnitude variations of the harmonic current between the wind farm and the VSC-HVDC system
仿真结果与基于耦合阻抗的分析结果一致,与不考虑频率耦合特性的阻抗分析结果相反。这说明:在判断风电-柔直系统振荡稳定性时,不可忽略阻抗重的频率耦合效应。
3.4 影响稳定性的主要因素
风电-柔直系统的运行状态会随着风速、负载等控制条件的变化而产生变化。以风电机组台数为例,如图9(a)所示,风电机组台数分别在0.5 s增加至10台,在4 s处增加至20台,在8 s处增加至30台,在12 s处增加至40台,在16 s处增加至50台。当风电机组台数增加至50台后,交流线路中出现13.2 Hz的谐波电流,谐波电流逐渐发散,最终在17 s引起风电-柔直系统失稳。风电机组台数为50台时的耦合阻抗特性如图9(b)所示,耦合阻抗行列式的虚部在13.2 Hz处出现过零点,根据式(11)稳定性判据,在此工况下系统存在13.2 Hz的不稳定振荡,与仿真分析结果一致。
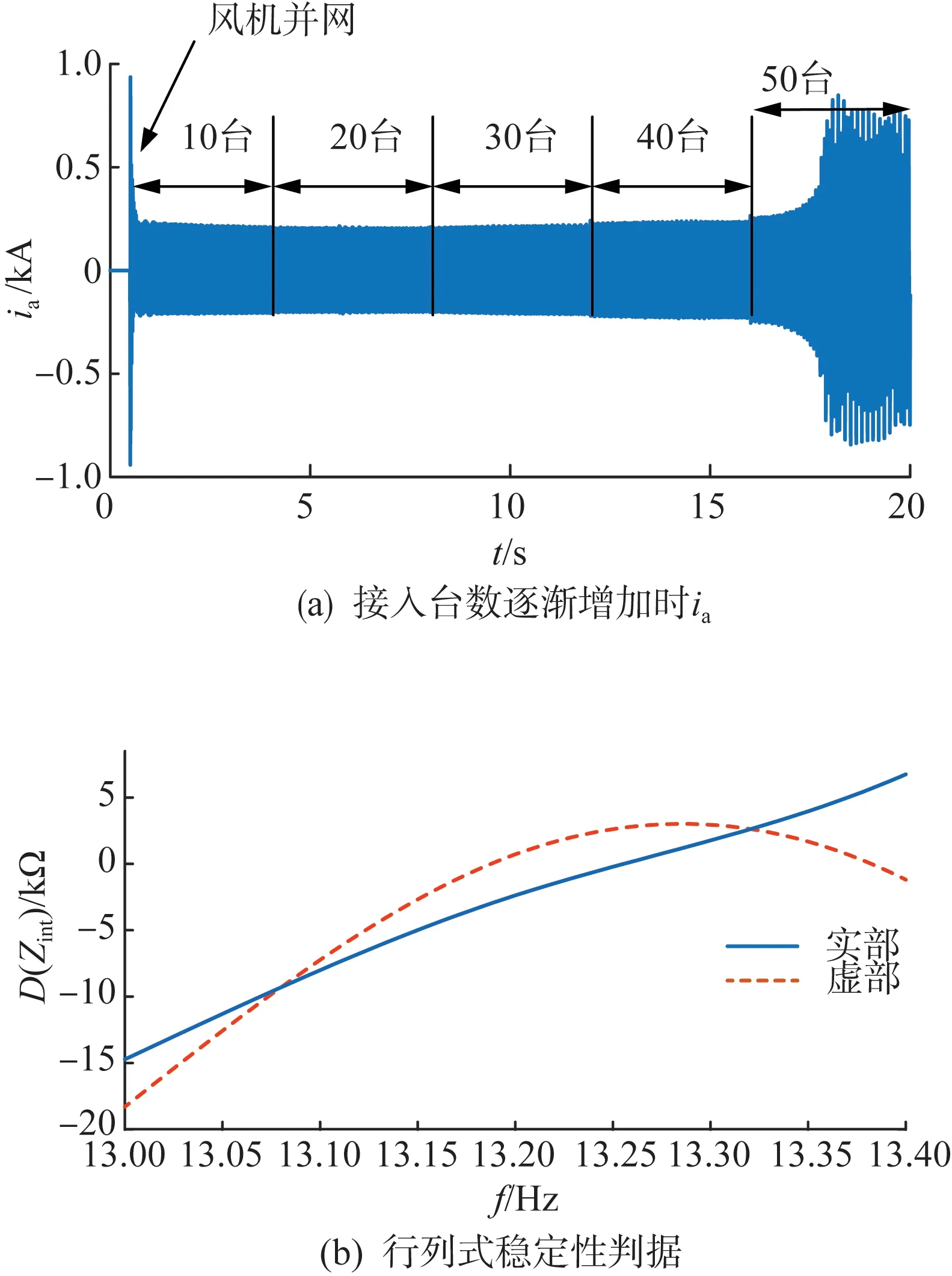
图9 风机台数增加时系统稳定性Fig.9 System stability reduces with the increasing number of wind turbines
结合仿真分析与聚合阻抗判据,分别列出了风电-柔直系统交流线路长度、出力程度、控制器参数对稳定性的影响。
交流线路长度:风电场过交流线路接入柔直系统,当线路长度的变化会影响风电-柔直互联系统的稳定性。如图10所示,随着线路长度在t1时刻从10 km切换到50 km,遂后在t2时刻从50 km切换到到100 km,接入点电流变化特性如图10所示。
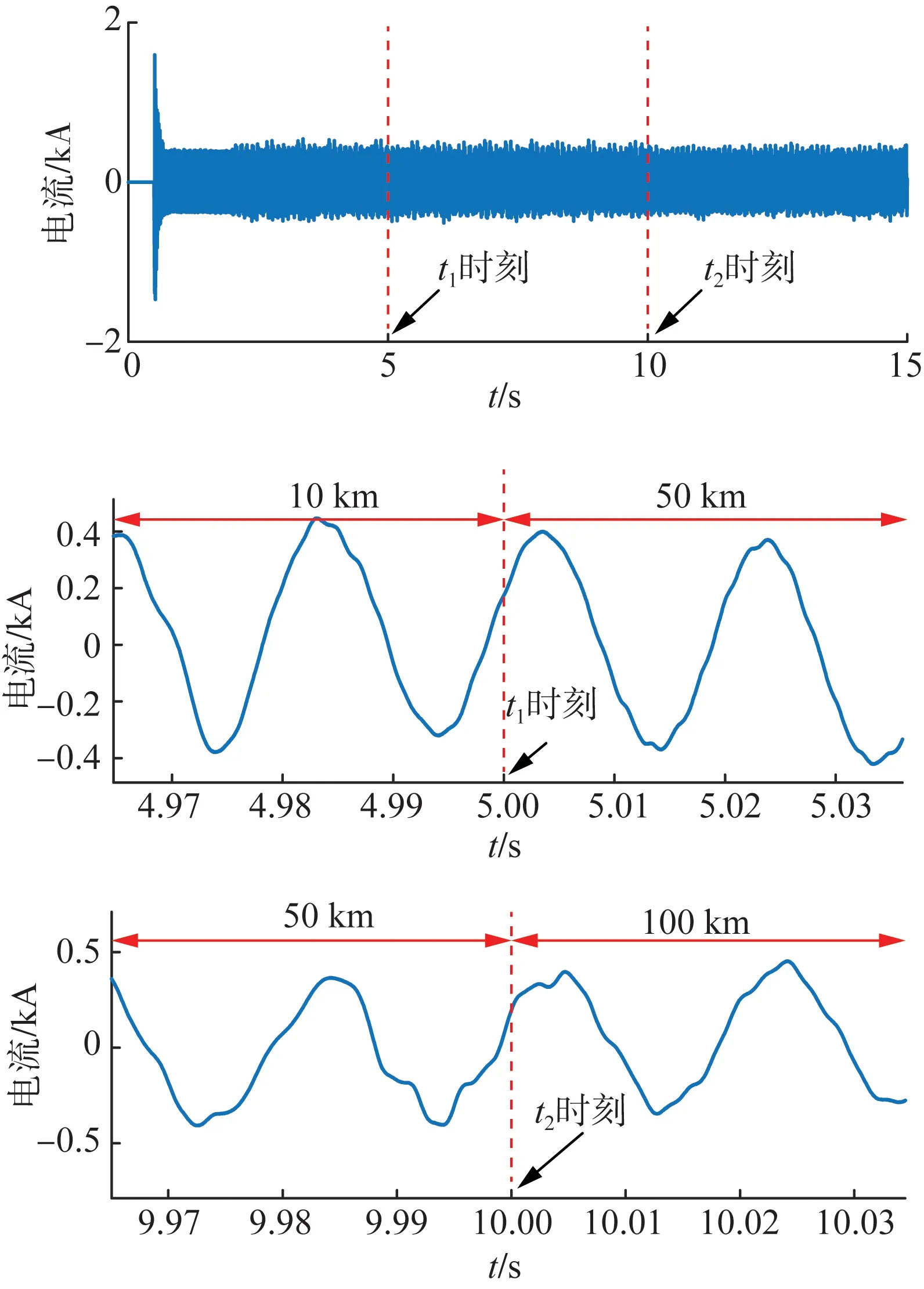
图10 交流线路长度变化对接入点电流影响Fig.10 Impact of changing length of AC line on the current at PCC
在次同步频段,线路阻抗仅为风电机组阻抗的5%左右,线路长度从10~100 km变化的范围内,对风电-柔直系统的稳定性影响较小。另一方面,由于仿真模型中风电机组台数较少,实际风电场中风电机组台数可达数百台,相当于风电场又并联上多台风电机组,此时风电场的等效阻抗下降,因此交流线路阻抗在聚合耦合阻抗特性中的影响就逐渐增大,此时线路长度的变化可能会对实际风电-柔直互联系统的稳定性产生影响。
风电场出力水平:风电场出力程度会根据系统运行工况动态调整。以处于临界稳定状态的风电-柔直系统为例,风电场出力程度逐渐变小过程中,振荡频率略微下降,振荡频率处的阻尼率先下降再上升,如表2所示。
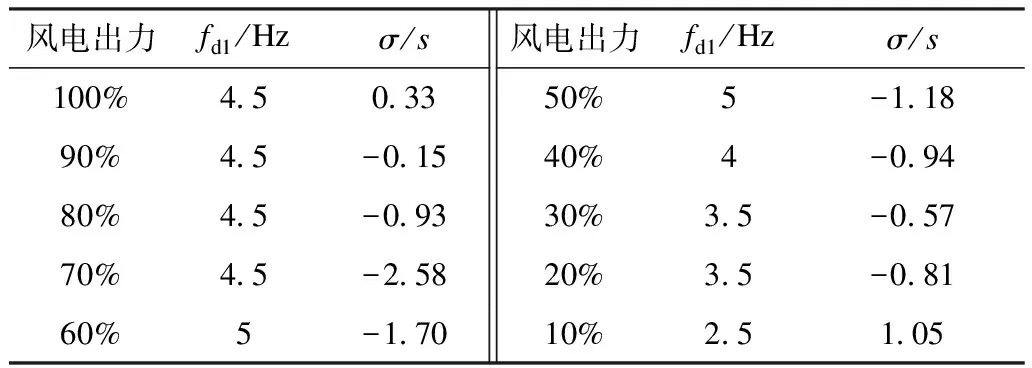
表2 风电场出力程度对稳定性的影响Tab.2 Impact of the varying output power of the wind farm on the system stability
控制器参数:风电-柔直系统中柔直变流器中采用了v/f控制。当交流控制器比例增益Kp为1时,接入点电流谐波含量较少;但是当Kp增至3时,接入点电流中出现了4.5 Hz的谐波,如图11所示。
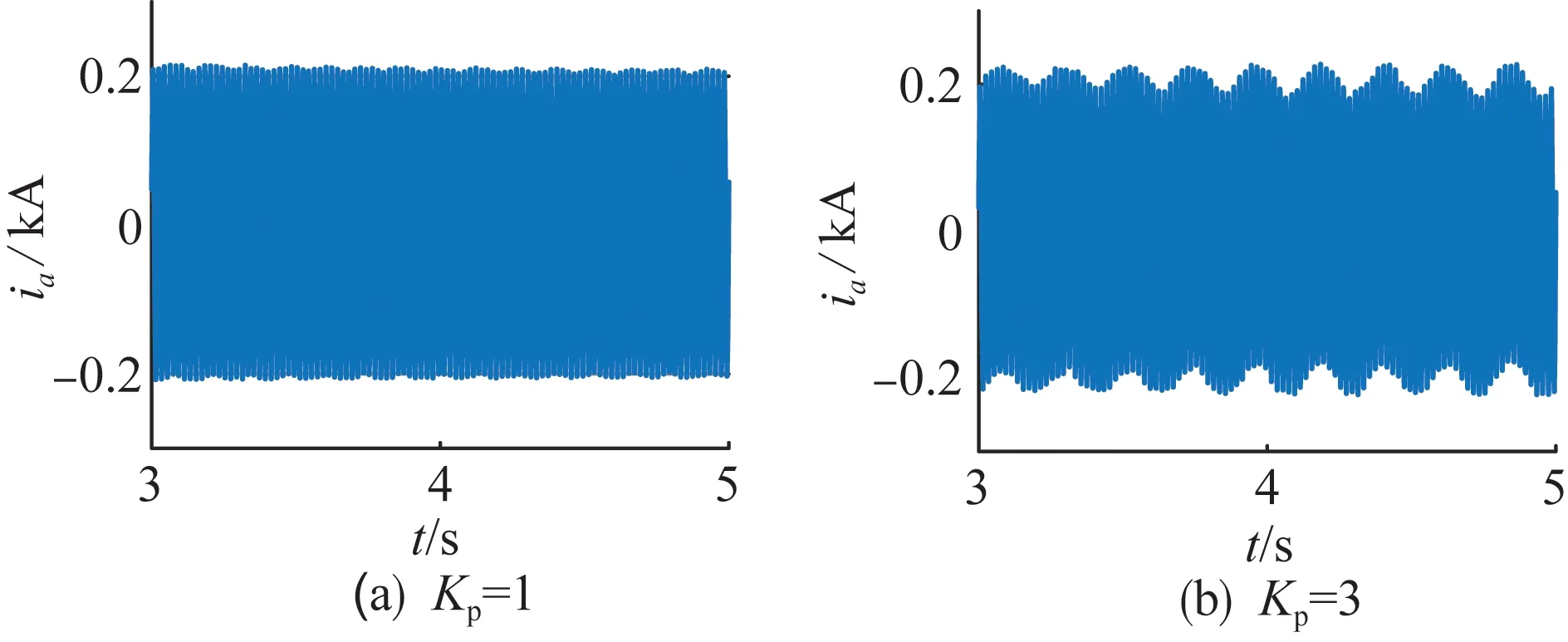
图11 控制器PI参数增大时接入点电流逐渐出现振荡Fig.11 Harmonic current gradually increases when increasing the gain of the controller
4 结论
本文针对风电-柔直系统的次同步针对问题,考虑次、超同步频率耦合效应,基于耦合阻抗模型分析了次同步振荡的稳定特性,并结合时域仿真研究了风电场机组台数、线路长度、风电机组出力水平、柔直变流器控制器参数等对振荡稳定性影响,得出以下几点结论。
1)风电-柔直系统中,次同步与互补的超同步频率之间存在明显的耦合效应,考虑该频率耦合效应并采用耦合阻抗模型才能准确判定系统的次同步振荡稳定性。
2)基于耦合阻抗模型及其聚合阻抗的频率特性可准确预测风电-柔直系统的次同步振荡风险,并可获取振荡的频率、阻尼等量化信息,为制订振荡抑制策略提供了依据。
3)风电场机组台数、出力水平和控制器参数对耦合阻抗影响较大,交流线路阻抗特性对次同步振荡的影响跟风电机组台数有关,风电容量越大,交流线路的影响也会增大。

