基于Bayes和Bootstrap方法的智能电表可靠性评估
李若茜,肖霞,梅能,柯航
(华中科技大学电气与电子工程学院,武汉 430074)
0 引言
随着智能电网的发展,海量智能电表投入运行。截至2017年底国家电网累计安装了4.24亿只,截至2018年底南方电网安装了8 815.72万只。智能电表的可靠运行关系到用户电费计量,同时,其可靠性评估结果可用于指导设备的检修、轮换工作[1 - 3],因此准确评估智能电表的可靠性具有重要意义。
目前针对智能电表可靠性评估已给出了较多解决方案。IEEE1413.1—2002标准[4]给出了4种电子设备可靠性预计方法:基于手册的可靠性预计、基于试验的可靠性预计、基于现场数据的可靠性预计和基于失效物理的可靠性预计。基于手册的可靠性预计根据元器件的质量、工作环境等由手册获得元器件失效率、结合串联模型得到系统的可靠性预计结果,文献[5 - 6]分别依据SR- 332、GJB/Z 299C标准预计智能电表可靠性。文献[7]结合智能电表特点及可靠性预计需求指出SR- 332更适用于智能电表的可靠性预计,然而该方法的结果依赖于更新较慢的预计手册,与实际情况存在偏差,通常仅用于设计阶段。基于试验的可靠性预计和基于现场数据的可靠性预计采用数理统计方法处理通过开展加速寿命试验(accelerated life test, ALT)、收集现场数据得到的数据进行智能电表可靠性评估,GB/T 17215.931[8]标准采用最小二乘法处理获得的ALT数据。文献[9]则将该方法用于现场失效数据的分析中。文献[10]采用遗传算法优化根据现场数据构建的极大似然函数得到模型参数,以上方法仅使用一种来源的数据,其结果的准确度有限,原因在于试验数据虽能涵盖智能电表整个生命周期但受限于试验施加应力同现场运行环境间差异、试验样本量等因素,其结果并不准确,而现场数据虽然样本量相对更大但由于截尾程度较深故不能涵盖其全生命周期。基于失效物理的可靠性预计在掌握设备结构、材料等信息的基础上,将开展应力分析得到的结果结合失效机理寿命模型得到准确的失效时间[11],但一些失效机理尚未建立准确的寿命应力模型,限制了该方法的应用。
融合多源数据进行可靠性评估的研究目前大多基于贝叶斯理论并围绕发动机、数控机床等[12 - 16]设备开展,应用于智能电表的研究不多,文献[17]通过加速退化试验数据与现场检测状态数据的融合对智能电表进行状态评估,文献[18]对ALT得到的失效数据和性能退化数据进行融合实现可靠性评估,但先验分布的确定是该方法的难点。
针对前述问题,本文提出基于Bootstrap和Bayes方法的智能电表可靠性评估方法,该方法通过Bayes理论融合ALT数据和现场数据,采用Bootstrap方法获取并解决先验分布的确定存在主观性的问题,得到的可靠性评估模型兼顾两种数据的优点,弥补两种数据的缺陷,对于智能电表可靠性评估工作具有指导意义。
1 数据融合的智能电表可靠性评估法流程
基于Bayes和Bootstrap方法融合ALT数据、现场失效数据的智能电表可靠性评估方法的框架如图1所示。

图1 基于Bootstrap和Bayes方法的智能电表可靠性评估框架Fig.1 Framework for reliability evaluation of smart meters based on Bootstrap and Bayes methods
融合现场失效数据与ALT数据的智能电表可靠性评估方法主要由以下3部分构成。
1)对现场失效数据的处理。采用传统参数估计方法处理现场数据求得总体的可靠性模型参数估计值;在获得模型参数的基础上,基于Bootstrap方法对总体多次抽样并重复参数估计过程,得到可靠性模型参数的先验信息。
2)对ALT数据的处理。ALT数据是在高于正常应力水平下得到的,需借助加速因子外推至正常条件下,作为后续似然函数构建的基础。
3)融合现场与试验数据的参数估计值求解。以现场数据处理后得到的参数离散分布作为先验分布,由外推至正常条件的试验数据构建似然函数,基于Bayes方法联合两种信息得到参数后验分布进而求得数据融合后的参数估计值。
2 基于Bayes方法的智能电表数据融合
2.1 Bayes方法
Bayes方法是一种以Bayes定理为核心的参数估计方法,该方法认为概率分布的参数为随机变量,且其估计值为根据样本信息不断修正先验信息得到的后验分布的期望值。
考虑到指数分布、正态分布等一些常用可靠性寿命分布可视为Weibull分布的特殊形式,本文采用如式(1)所示的Weibull分布建立智能电表的不可靠度模型。
(1)
式中β和η分别为形状参数和尺度参数。
模型参数后验分布的离散形式如式(2)所示。
(2)
式中:π(βi,ηi)为β和η的先验分布;L(t|βi,ηi)为根据样本构建的似然函数;g(βi,ηi|t)为参数的联合后验分布。
基于该后验分布的参数β、η后验期望计算式如式(3)—(4)所示。
(3)
(4)
采用该方法进行参数估计的难点在于先验分布的确定。常用的确定方法包括依赖经验的主观确定法和客观法,客观法又分为基于同等无知原则的Bayes假设和总结过去资料两种方法,但同等无知原则在高可靠系统的评定中不可取[19],故本文根据已有的现场失效数据或试验数据确定先验分布。
由式(2)可知,先验信息和样本信息提供的信息量大小虽然有所差异,但两者在参数估计中地位对等[20]。考虑到现场数据样本量更大,因此本文将现场数据作为先验信息来源、试验数据作为似然函数构建依据。
2.2 ALT数据的处理
ALT对样本施加高于正常条件的应力以在短时间内获得高可靠设备寿命数据[21]。将该数据应用于评估设备实际运行条件下的可靠性或寿命,需借助加速模型导出的加速因子对试验数据进行外推处理。
高温、高湿试验下获得的数据可通过Peck模型处理,该模型及其导出的加速因子(acceleration factor, AF)表达式分别如式(5)—(6)所示,ALT得到的寿命数据乘以加速因子即得到等价的正常运行条件下的寿命数据。
(5)
(6)
式中:A为常数;Ea为活化能,一般取0.9 eV;n为常数,一般取3;k为玻尔兹曼常数;ρu和ρs分别为正常使用条件和加速试验条件下的相对湿度;Tu和Ts则为对应条件下的温度。
通过ALT得到的数据包含失效数据和截尾数据两部分,前者提供了准确的样本寿命、后者给出了样本寿命的取值范围,似然函数应由两个部分共同构成。假设样本总数为N,失效样本数为r,则该样本对应的似然函数如式(7)所示。
(7)
式中:f(ti|β,η)为概率密度函数在ti处的取值;R(TR|β,η)为可靠度函数在Tr处的取值。
将Weibull分布的概率密度函数、可靠度函数代入式(7)得到似然函数,如式(8)所示。
(8)
式中:ti为第i个失效样本对应的失效时间;Tr为截尾时间。
3 基于Bootstrap法的先验分布获取
3.1 Bootstrap方法
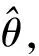
该方法后续也被用于参数区间估计的研究中,因此本文采用该方法获取参数的先验分布,基于Bootstrap方法获取Weibull分布的参数联合先验分布的主要步骤如下。
1)依据现场数据进行参数估计,得到形状参数和尺度参数的估计值β和η。
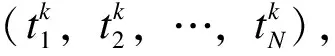
3)由Weibull分布中β和η独立得到式(9)所示参数的联合先验分布。
(9)
3.2 现场数据及其Bootstrap子样的处理
如前所述,先验分布的获取依赖于对样本及其Bootstrap子样的参数估计,传统参数点估计方法有最小二乘法和极大似然估计法(maximum likelihood estimation, MLE),合适的参数估计方法应当结合样本的特点确定。
现场数据来源于对实际运行的大量智能电表的故障收集,智能电表的高可靠性[23 - 24]使得同一批投运的装置中故障数量占比并不大,得到的现场数据实际是样本总数N很大,而失效数量r占比很小的截尾样本。采用MLE方法时,一种处理为使用失效数据和截尾数据得到式(7)所示的似然函数,但较大的样本总数使得表达式复杂、求解困难;另一种方式将样本转换为截尾分布后只使用失效数据列出似然函数,但该方法的求解精度随截尾程度的增加而降低[25],不适用于截尾程度过深的现场数据。最小二乘法则对截尾样本、完全样本均适用。
对式(1)所示的Weibull分布做线性化处理得到式(10)。
(10)
采用最小二乘法结合样本对上式进行参数估计时,代入样本点(ti,F(ti)), 其中i为样本升序排列的序号,F(ti)采用近似中位秩计算、同时构造新的变量如式(11)所示。
(11)
则采用最小二乘法进行线性拟合得到的参数β、η的计算式分别如式(12)—(13)所示。
(12)
(13)
样本的Bootstrap子样的参数计算式要求同上述计算式保持一致,故抽样过程中从Fn(β,η)中抽取N个样本,升序排列并剔除大于截尾时间Tr的样本后采用同样的方法进行处理。
4 实例分析
本节以某厂家某型号智能电表的实际ALT数据和现场失效数据为例,采用本文给出的可靠性评估方法进行处理并对结果进行分析。
4.1 算例数据处理
在ρs=95%、Ts=65 ℃的条件下对30个样本开展ALT,由式(6)可知外推至ρu=75%、Tu=20 ℃的正常条件时,加速因子取值为234,由此得到的23个ALT失效数据及其外推结果在表1中给出,该样本的等效正常使用条件下截尾时间为146 016 h。

表1 ALT失效数据及其外推结果Tab.1 ALT failure data and their extrapolation results
同时对现场数据进行收集,得到某批次投入现场使用的同型号智能电表共2 312只,故障表计共53只,相应的失效数据如表2所示,该样本截尾时间为89 784 h。
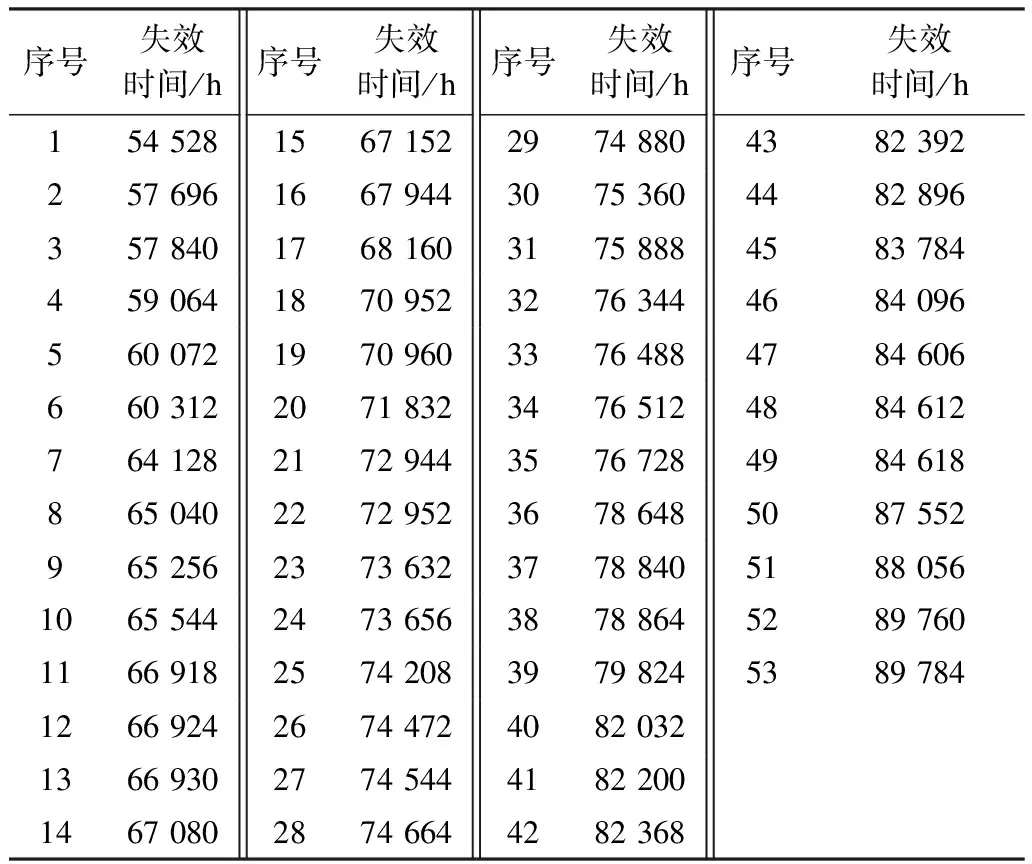
表2 现场失效数据Tab.2 Field failure data
由现场数据根据式(12)—(13)求得形状参数β=7.30,尺度参数η=140 700.17,从对应的Weibull分布中进行10次Bootstrap重抽样与参数估计,得到各子样的参数估计结果如表3所示。
以表3数据为基础构建Weibull分布的参数联合先验分布,根据Bayes方法基于该离散先验分布和试验数据,由式(2)得到参数的后验分布,根据式(3)—(4)得到对应的后验期望值为β=5.74、η=130 818.18。

表3 Bootstrap子样参数估计结果Tab.3 Parameter estimation results of Bootstrap samples
本文所提方法在上述算例场景下的应用流程图如图2所示。
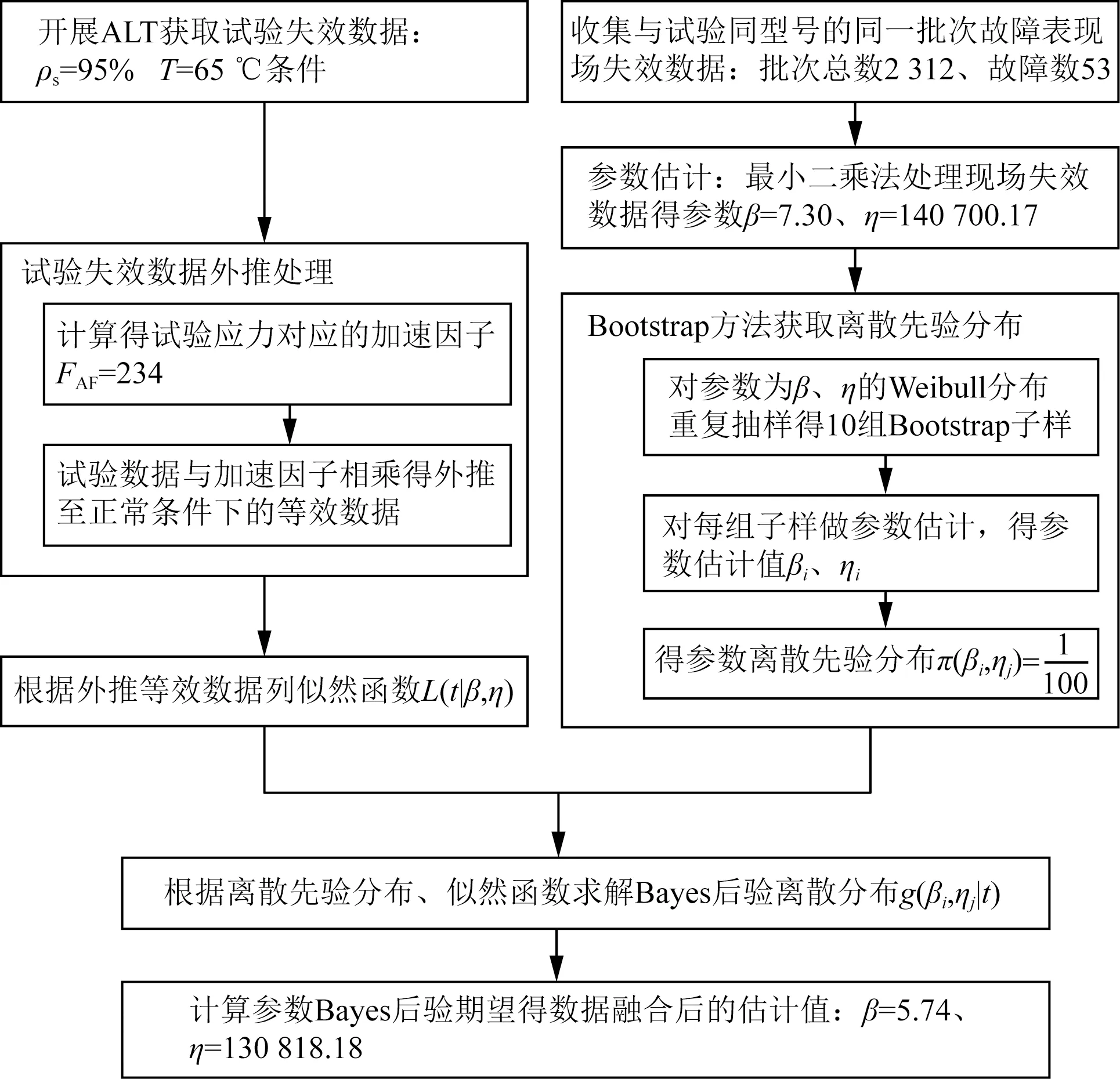
图2 算法在算例应用下的流程图Fig.2 Flow chart of the algorithm in a calculation case application
4.2 结果对比分析
将本文方法得到的模型与基于现场数据评估、基于ALT数据评估得到的模型进行对比,后两种方法的模型采用最小二乘法单独对表1的试验数据、表2的现场数据处理得到,参数估计值由式(11)—(13)计算。3种数据源对应的模型参数整理如表4所示,对应的可靠度随时间变化曲线及现场数据如图3所示。可以得到如下结论。

表4 不同数据源的参数估计结果Tab.4 Estimation results of parameters based on different data source
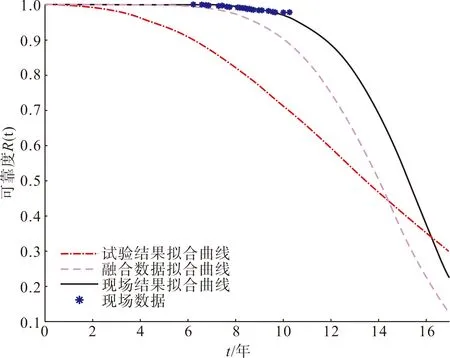
图3 三种不同数据源可靠性评估结果对比Fig.3 Comparision of reliability evaluation results based on three different data source
1)在有现场数据的时间段,仅采用ALT数据得到的智能电表可靠性模型预计的可靠度指标明显低于实际运行数据反映的情况。
2)仅采用现场数据得到的智能电表可靠性模型对现场数据拟合效果较好,但由于现场数据集中在全生命周期的前半段,对于缺乏现场数据支撑的范围无法判断模型评估效果的优劣。
3)本文所提方法得到的智能电表可靠性模型在前半段相较于仅依据试验数据得到的模型更接近现场实际情况;在无现场数据的后半段由于融合了涵盖全生命周期的试验数据,相较于仅依据现场数据得到的模型其评估结果有一定的数据作为支撑,可以用于智能电表全生命周期的可靠性评估。
5 结语
本文提出了一种基于Bayes和Bootstrap方法的智能电表可靠性评估方法,融合现场数据和试验数据解决基于单一数据源的可靠性模型不够准确的问题,采用Bootstrap方法处理现场数据解决数据融合中先验分布的获取依赖主观经验的问题。
实例分析结果表明,该方法得到的模型能够较好地反映现场实际可靠度水平,同时在现场数据缺失段利用试验数据,综合两种数据各自的优点,可用于解决智能电表全生命周期的可靠性评估问题,对智能电表的轮换工作具有一定的参考价值。

