Radarsat-2影像的空间基线误差去除方法研究
陈建明 匡薇 孙卫东 刘超
(1.新疆维吾尔自治区地质矿产勘查开发局信息中心,新疆乌鲁木齐 830011;2.新疆地质调查院,新疆乌鲁木齐 830011)
0 引言
Radarsat-2是一颗搭载C波段传感器的高分辨率商用雷达卫星,具有3-100 米分辨率成像能力,重访周期仅24 天,可用于大范围监测地表形变[1]。由于Radarsat-2卫星存在零件松动的情况,导致基线不能正确估计,加拿大MDA 公司也正致力于纠正Radarsat-2轨道数据的精度问题[2]。国内外很多使用Radarsat-2数据的学者都尽量避免提及基线误差对结果的影响,对于Radarsat-2 数据呈现的非线性特点,目前并没有有效去除该误差的方法[3-5]。本文针对现有的Radarsat-2影像空间基线不能正确估计的问题,在了解到Radarsat-2 影像空间基线误差呈现弱二次曲面特点基础上[6-10],提出一种不用直接估计空间基线,而在干涉相位解缠后去除空间基线误差的方法。该方法是在相位解缠后,针对感兴趣区,采用二次曲面拟合基线误差,并通过相位相减来实现误差的去除。同时,本文将对比误差去除前后效果,以及传统基线估计方法对结果的影响来评估该方法的准确性。
1 研究区概况
研究区位于安徽省西北部,如图1。区内以平原为主,气候上属暖温带与亚热带的过渡地区,四季分明,春暖多变,夏雨集中,秋高气爽,冬季寒冷。区内发育多条水系,地下水储量丰富,过度的地下水开采导致该区域沉降明显,城区大面积地面沉降,地面沉降累计最大沉降量为1567.2mm,有关资料表明,该区仍以30-40mm/a的速度下沉[11]。
2 数据和方法
2.1 数据
2.1.1 影像数据
实验选取Radarsat-2 影像,数据类型为SLC 数据。本实验数据为标准波束模式,VV 极化方式,距离向分辨率为25m,方位向分辨率为26m,标称景大小为100km×100km,数据商提供的数据为竖三联景,即景大小为100km×300km。
DEM 选用欧空局免费提供的SRTM DEM 数据,分辨率为90m。
2.1.2 数据预处理
差分雷达干涉测量(D_InSAR)技术是地表形变监测领域的有效手段,数据处理采用GAMMA 软件,数据处理流程包括影像配准及重采样、多视处理、生成干涉图、基线估计、DEM 准备、差分处理、相位解缠等步骤。
2.2 方法
2.2.1 相位解缠后的Radarsat-2 影像的空间基线误差特点及去除方法
由于Radarsat-2 影像的空间基线误差在干涉图中相位呈现出非周期性-π至π的变化特征,各图像没有统一的误差形态,不能用同一个模型去模拟整个图像的基线误差。图2为采用精轨数据校正后的差分干涉图,图中大型条纹变化均为基线误差影响。但相位解缠时,空间基线误差也会被当作缠绕相位解缠,相位解缠后的基线误差呈现出一个二次曲面的特点,如图3所示。所以本文将拟合一个二次曲面,用相位解缠后的图像减去拟合的二次曲面值,即得到沉降值。
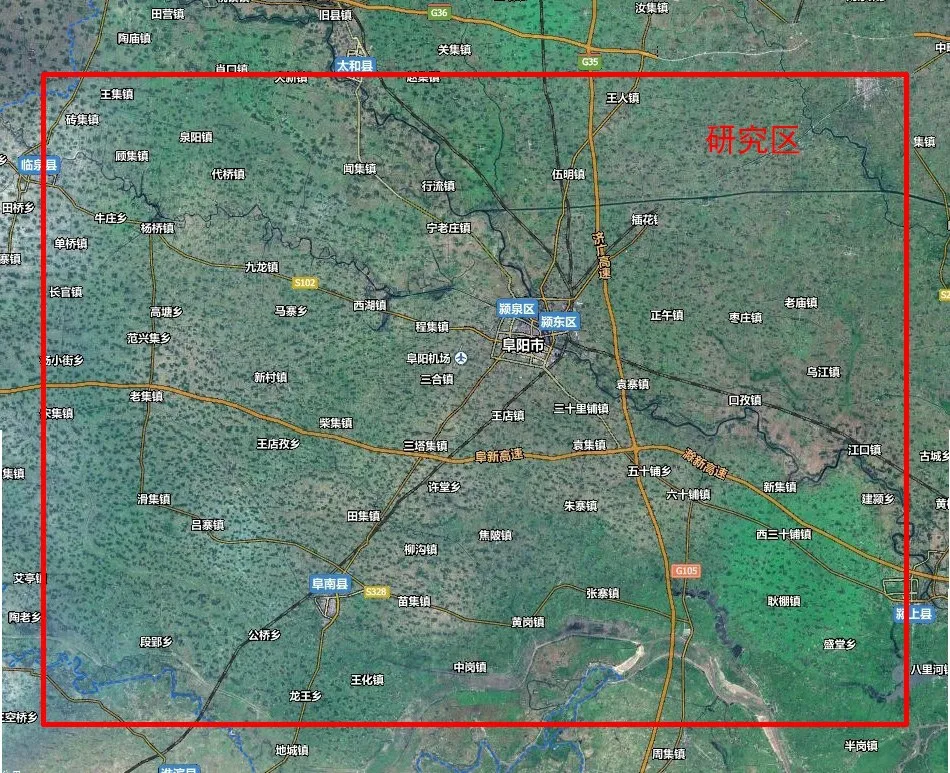
图1 研究区示意图

图2 含基线误差的差分干涉图
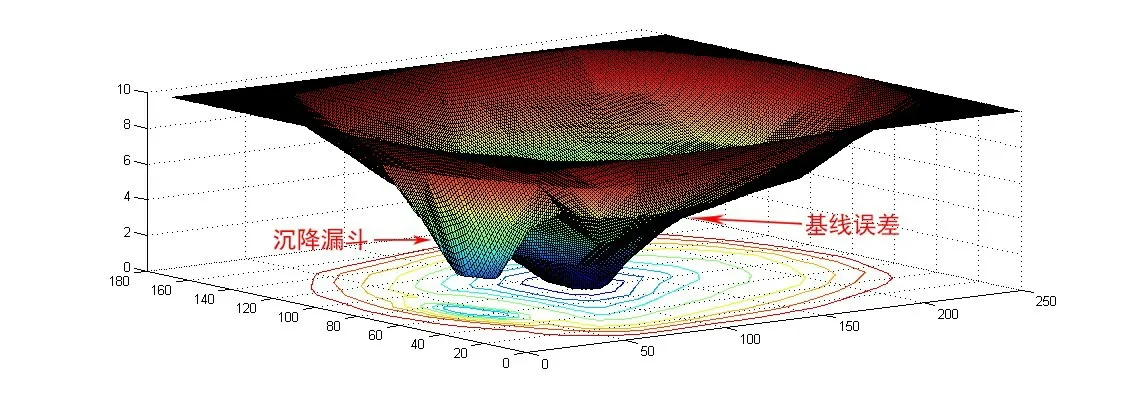
图3 解缠后干涉相位示意图
当然,为了避免噪声的干扰,最好是针对感兴趣区拟合二次曲面,这样得到的结果更加准确。
2.2.2 二次曲面拟合算法
二次曲面的拟合采用最小二乘法,它通过计算残差的平方和最小时候的参数来拟合曲面。二次曲面拟合算法如下:
设曲面上的任一点的高度值z=f(x,y)可写成:
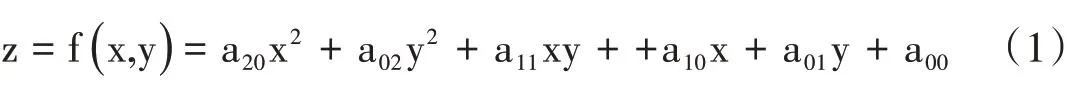
假设实验数据为(xi,yi,zi)(i=1,2,…,N),由于多项式曲线不一定通过所有的点,所以多项式在(xi,yi)所算出的值与观测到的函数值zi之间存在差距,即误差或剩余量,用Ri来表示。
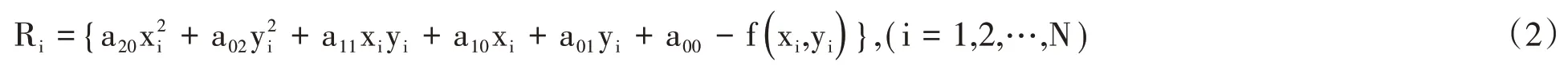
这样就有N 个误差方程。对于N 个数据(xi,yi,zi)去求系数aij的最佳值就是能使误差Ri的平方和最小的那些值。因此,为了选择适当的系数,要使误差的平方和:
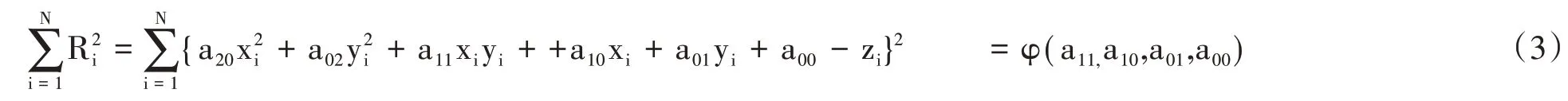
为最小值,必须适合下列方程组:
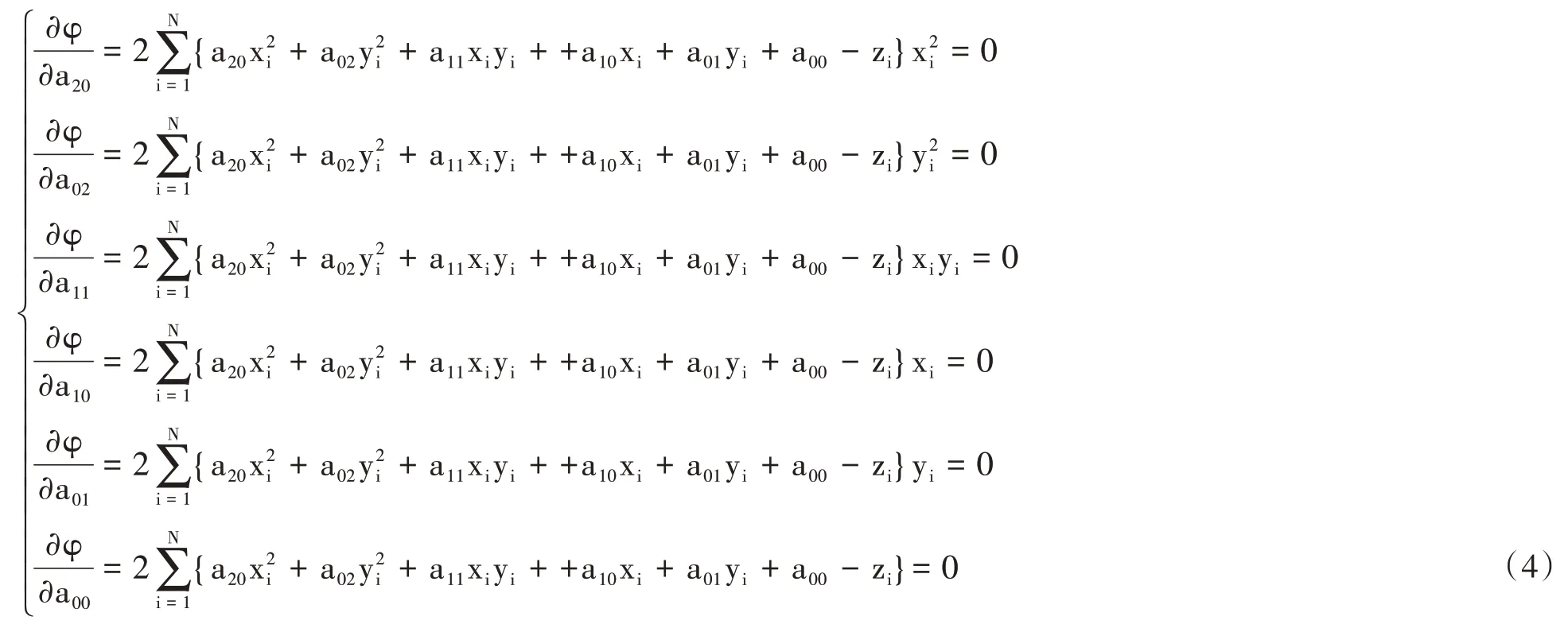
即有:
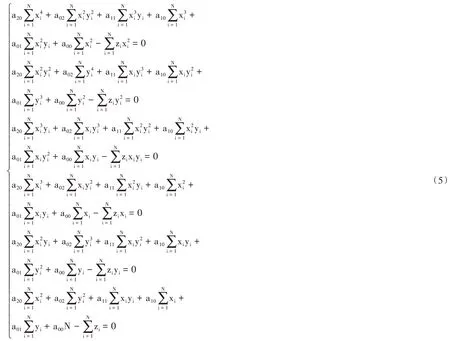
为了得到正规方程组,须计算以下各和:
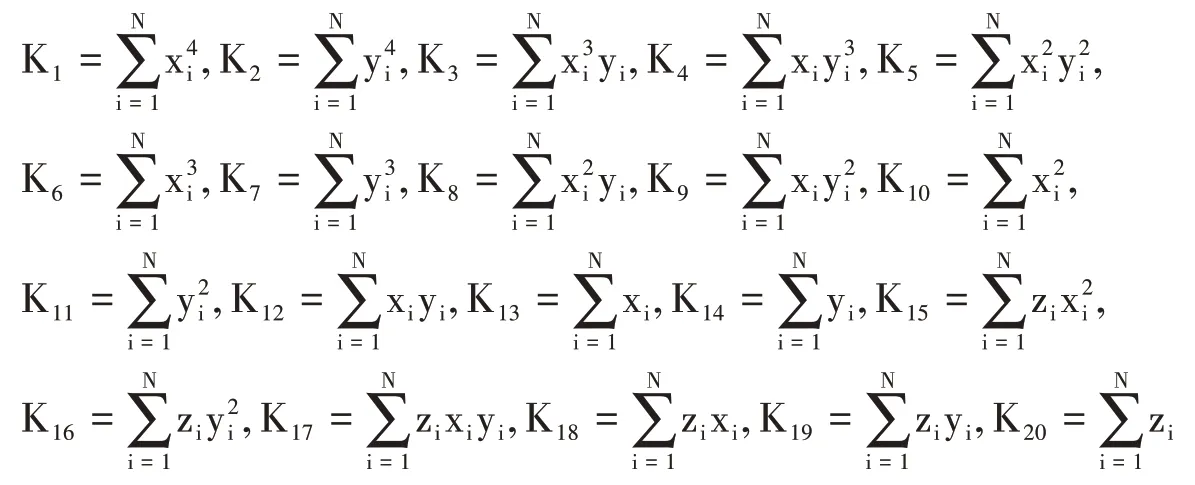
则有
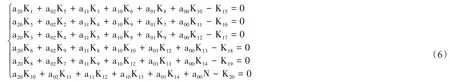
根据cramer法则:
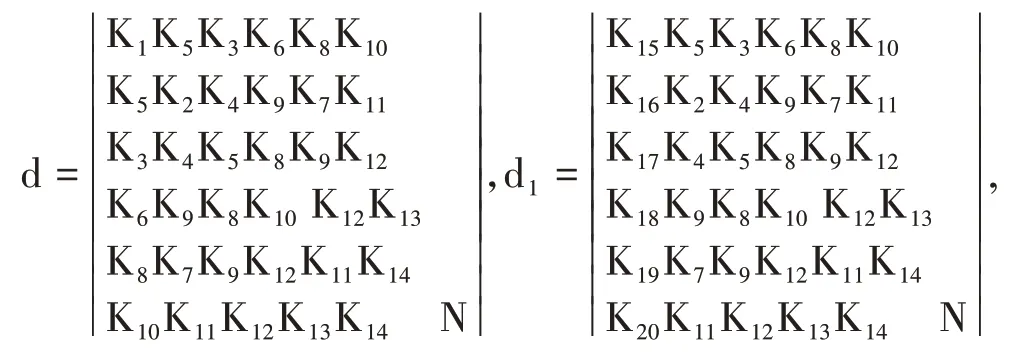

带入式(1)即得拟合二次曲面方程:f(x,y)=a20x2+a02y2+a11xy++a10x+a01y+a00
2.2.3 Radarsat-2影像的基线误差去除步骤
(1)获取相位解缠后的图像,图像数据类型为float型,暂命名为data1;
(2)采用滤波方式平滑图像,建议采用均值滤波,滤波后的图像暂命名为data2;
(3)将相位解缠后的图像与强度图叠加显示以选择感兴趣区,该感兴趣区须具有较明显的基线误差特征;
(4)用data2 数据在感兴趣区范围内拟合曲面,得到参数a20,a02,a11,a10,a01和a00,并用该参数计算整个图像的z值,生成的拟合曲面图暂命名为data3;
(4)将data1和data3做差分处理即得去除基线误差的沉降图,暂命名为data4。
3 Radarsat-2 影像的空间基线误差去除实验及结果分析

图4 基线误差去除前后对比图
实验采用安徽地区的Radarsat-2雷达影像,主图像获取时间为20120416,辅图像获取时间为20130318,感兴趣区选在影像底部的阜阳地区。实验数据已采用精轨数据校正过。按本文方法去除基线误差,基线误差去除前后对比图如图4 所示,图4 为0416_0318.unw和0416_0318.unw_base生成的图片。
图中方框区域为感兴趣区,可以看出相位解缠图中即便是没有发生沉降的区域,由于基线误差的影响仍然有明显的条纹变化,且这些条纹变化并不规律。阜阳地区属于平原区,该区域内条纹变化较为规律,有明显的二次曲面特点,故选择该区域进行基线误差去除。对于感兴趣区内,在基线误差去除后城市区域的沉降漏斗明显地显示了出来,而未发生沉降的区域则没有了条纹变化。对于感兴趣区以外的地区均为不可信区,图中方框以外的区域,其误差并未得到有效去除,其结果不能用于成果显示。这说明基线误差的存在并不影响解缠,且解缠后二次曲面拟合去除基线误差效果较好。
4 结论
通过本文的分析,笔者得出如下结论:
(1)Radarsat-2影像的空间基线误差可在解缠后通过对感兴趣区进行二次曲面拟合的方法去除。
(2)Radarsat-2影像存在较为严重的空间基线误差,该误差在解缠后误差相位呈现弱二次曲面的特点,且在相位解缠后去除效果较好。去除方法为对感兴趣区进行二次曲面拟合,通过相位相减的方法将空间基线误差去除。
(3)误差去除后的图像,感兴趣区内数据可信,感兴趣区外数据不可信。
(4)该方法使得从Radarsat-2影像中定量提取沉降信息成为可能。

