基于任意四边形镶嵌的四方连续图案智能化设计技术研究

刘肖健，吕芸芸，赵赢男，黄鑫宇

（浙江工业大学，杭州 310023）

在服装面料、室内装饰板、背景底纹等平面设计中，经常需要基于图形单元对一个无限的平面进行无交叠填充，即图形单元平铺布置，相互之间不存在交叠。四方连续图案是完成此类任务最常用的手段，对图案中的图形单元有分布均匀、疏密平衡等美学要求，同时还要避免简单复制带来的僵硬感和机械感。由于选定的图形单元其本身的形状并不规则，且多个图形单元的组合方式灵活多变，所以画面布置与调整将比较耗时。笔者利用任意四边形无缝镶嵌的原理来解决上述设计问题，开发了智能化的设计工具，以提高设计师的工作效率。

1 概述

四方连续是一种常见的平面图案类型[1]，属于对称图形的一种。Washburn 等[2]基于对各国传统纹样的研究，梳理了多达几十种不同的对称规则，其中绝大多数可用于四方连续图案的构造。四方连续图案的自动生成技术在计算机图形领域已有较长的研究历史，如李宝德等[3]早在1992 年就创造了面料四方连续图案的自动生成算法，实现了图块的复制及跨边界单元的处理；金兰名等[4]提出了连续式、比例式、分段式、整体式等四方连续图案的设计手段，可以快速完成符合工艺要求的织物图案设计；刘艳等[5]给出了重叠式四方连续的构造规律，并对织机效果进行了数字模拟；刘肖健等[6]基于二进制的编码方式，实现了中国古代墙洞填充四方连续图案的自动设计。

镶嵌图案指由一种或有限的几种图形单元通过无缝拼合得到的图案。各国传统纹样中均存在镶嵌图案。荷兰艺术家Escher 在镶嵌图案方面的创意和探索，引起了科学界和艺术界的兴趣，并引发了大量研究[7]。Naimia 等[8]对Escher 的连续镶嵌网格构造原理给出了数学证明；Fratta 等[9]改进了任意方向的3D 单元镶嵌方法，对Escher 的艺术设计思想给出了数学解释；Liu 等[10]利用Escher 风格的无缝图案镶嵌技术，解决了切割材料的排版和节约问题；Lin 等[11]开发了一个软件系统，主要用于生成渐变类型的Escher 镶嵌风格；Zhou 等[12]基于曲线自动构建装饰图案的方法，为非专业用户提供了一个可以绘制复杂装饰图案的工具；Adanova 等[13]对镶嵌式图案的设计方法进行了探索，给出了基于单元分组的创新方法；Hu 等[14]采用连续优化和组合优化相结合的方法，开发了利用不规则瓷砖进行无缝镶嵌的技术。镶嵌图形也被大量用于艺术创作之外的领域，如Mizzi 等[15]利用镶嵌图案原理来设计材料的微结构，实现对材料性能与形态的精确控制；Schumacher 等[16]根据美学性能和功能性需求来设计镂空建筑材料的四方连续图案。

任意四边形的可镶嵌性可以用于解决艺术设计、材料设计、制造工艺规程等领域的问题。笔者根据平面艺术设计中的填充式四方连续图案，把镶嵌单元从传统的直边四边形拓展到曲边四边形，在可镶嵌性的前提下，开发了可供设计师自由发挥的创意工具。同时把镶嵌单元用作其他图形元素的“外壳”，通过丰富的形态变化来满足不规则图形元素均衡分布的需要。

2 基本原理

2.1 直边四边形的镶嵌

基于初等几何学可以证明，任意四边形单元均可无缝镶嵌[17]，见图1。

图1 四边形的无缝镶嵌Fig.1 Seamless tessellation of quadrilaterals

基于四边形镶嵌的四方连续，需要利用4 个相同的四边形单元，通过旋转、移位来构造出一个复合单元，然后利用复合单元进行常规的阵列操作。在四边形内填入图形元素，令其符合一定的美学原则，完成镶嵌后再隐藏边框，即可得到所需的四方连续图案，见图2。另外，也可以事先进行内部图形元素的布置，然后构造出一个四边形进行紧密围绕，并彼此调整到位。非凸四边形（即四边形包含大于180°的内角）也可以无缝镶嵌，图2a 即使用了一个非凸四边形单元。

图2 四边形镶嵌得到的四方连续图案Fig.2 Square continuous patterns generated by tessellation

2.2 曲边四边形的镶嵌

图1b 的复合单元由四边形各边进行反向贴合得到，因此四边形的边不一定是直线，只要是相对直边中点对称的曲线（如正弦曲线）均可进行无缝镶嵌，见图3。

图3 曲边四边形单元的镶嵌Fig.3 Tessellation of curve-edge quadrilaterals

利用曲边四边形来调整图案的紧凑度，见图4。对称曲边四边形的可镶嵌性给图形元素的布置提供了极大的灵活性。例如，可以将图2a 单元四边形的边调整为曲边，从而使四方连续图案变得更加紧凑，见图4a。

比较图4b 与图2c，可以看出，图4b 的空间布置更加紧凑，留白更均匀。曲边四边形的无缝镶嵌也可以用于切割加工的排版设计，在四边形基础上，进一步设计出符合可镶嵌条件的自由形状来包裹待切割单元，从而最大限度地利用材料。

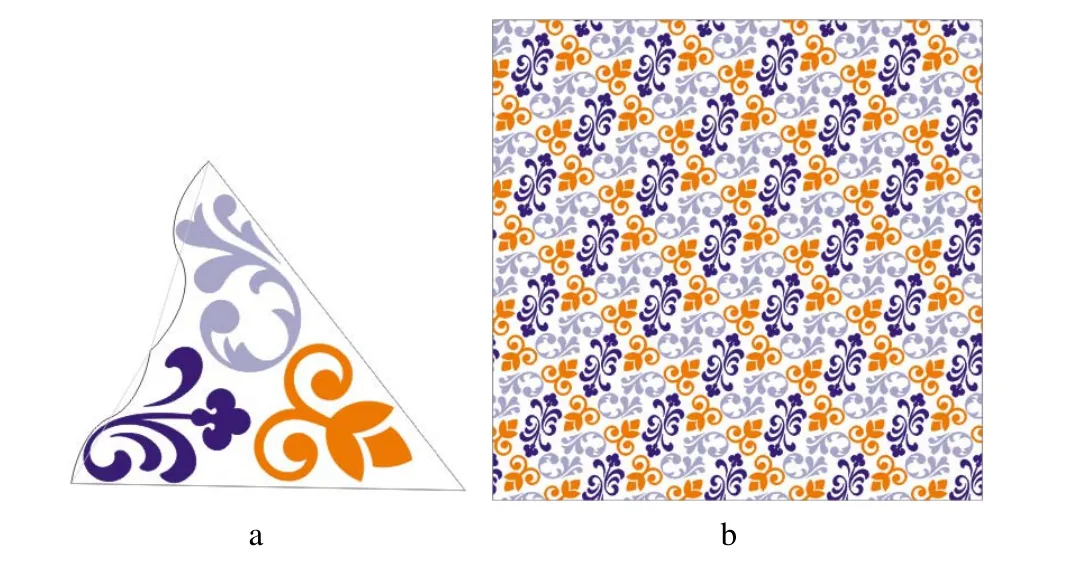
图4 利用曲边四边形调整图案紧凑度Fig.4 Regulation of pattern tightness with curve-edge quadrilaterals

3 四方连续图案智能化设计的技术实施

3.1 功能架构

为实现上述四方连续图案的智能化设计，基于平面设计师常用的矢量设计软件CorelDraw 来进行技术开发。CorelDraw 具有丰富的图形设计功能，图形元素的设计和布局及四边形绘制等单元设计工作可以由设计师手工完成，四方连续图案可以通过四边形的智能化识别和镶嵌等自动化方式完成。智能设计技术充分融合设计师的设计思想，通过人机协作的方式进行工作。四方连续设计的技术流程与界面见图5。

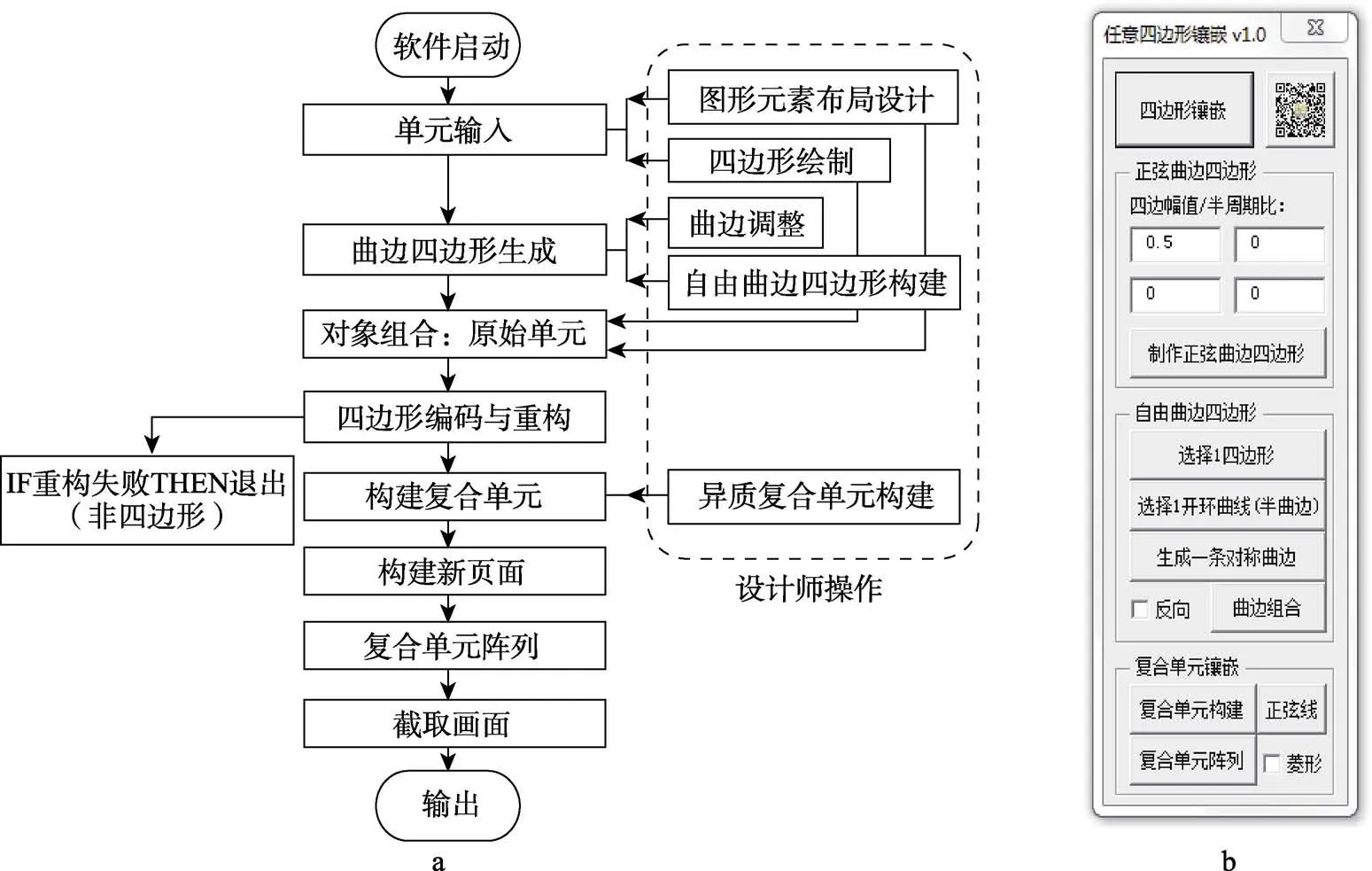
图5 四方连续设计的技术流程与界面Fig.5 Technical process of the pattern design and the user interface

设计师的工作集中在前期，主要内容是手工构建基本图案单元（如图2a、图4a），具体包括单元内部图形元素的布置和包围四边形的绘制，程序提供辅助工具，从而确保设计师绘制的曲边四边形具有可镶嵌性。复制阵列等工作交由程序处理。平台软件CorelDraw 提供了方便的图形处理函数，使开发工作可以控制在2 周之内，且设计师可以胜任开发工作，不需要职业程序员的介入。由于最体现创意价值的关键性工作均由设计师完成，且程序设置了对设计师创建的图形进行智能识别的算法，所以需要用户填写的参数很少，可用性良好。

四方连续设计界面分为4 个部分：基于四边形单元生成镶嵌图案，选定单元图形后，点击上方最大的按钮即可生成四方连续图案；生成正弦曲边四边形，在直边四边形基础上给出4 条边的波动幅度参数，把直边四边形转化为正弦曲边四边形；生成自由曲边四边形，在直边四边形的基础上，利用用户手绘的自由曲线生成可镶嵌的自由曲边四边形；基于复合单元生成镶嵌图案，在四边形单元基础上构建复合单元。

3.2 曲边四边形的可镶嵌性

不是所有的曲边四边形都可以无缝镶嵌。可镶嵌的曲边四边形需要满足一个条件，即各曲边均为直边中点的中心对称曲线。以下使用2 种方法构建曲边：第1 种是基于一条直边来构造一条正弦曲线形状的曲边，并设定一个参数让用户输入，从而控制各边正弦曲线的起伏高度和起伏方向；第2 种是由用户手工构造任意形状的自由曲边。

第1 种正弦曲边可以满足一般性的四方连续图案的设计，主要用于单元内部的图形元素填充。笔者基于直边构建正弦曲边，采用节点偏移的方法，即在直边上均匀取点，然后使其向直边法线方向偏移，偏移量的大小用正弦函数计算，最大偏移量（即正弦波的峰值高度）根据用户输入的参数值来确定。基于几种不同偏移量参数生成的曲边见图6。

图6 正弦曲边的生成Fig.6 Generation of Sine curve edge

用户可以在图5b 界面上部的4 个输入框中，输入4 条边的正弦曲线波幅参数。如果参数值为0，则该边保持为直线；如果为负值，则正弦波起伏方向相反。用户也可以通过界面中的“正弦线”按钮将一条直线快速变为正弦曲线（波幅取自界面上的第1 个参数），然后经过手动压缩变形（并不改变其对称性）处理后参与组建曲边四边形。有时正弦波形状的曲边四边形不能满足用户的需求，因此需要构建自由形状的曲边。对此，程序提供了辅助工具，从而确保用户可以构建出满足可镶嵌条件的曲边四边形。

用该辅助工具构建一个自由曲边四边形的过程如下：选择一个直边四边形（程序会检测所选的图形是否正确）；选择一条开环曲线，该曲线将被用作曲边四边形的半条曲边；将开环曲线复制、缩放并旋转180°后，与原曲线融合成一条对称曲线，形成一条可镶嵌的曲边；用鼠标在直边四边形需要替换的边的附近进行点击，程序会搜索附近的直边，并将曲边移动到位，使其两端点与直边两端点重合；选择生成的四条曲边（或直边），将其组合成一个曲边四边形。界面上的“反向”复选框用于确定曲边替换直边时，是否需要基于直边进行两侧翻转。自由曲边四边形的生成见图7。

图7 自由曲边四边形的生成Fig.7 Generating free curve-edge quadrilateral

3.3 四边形的识别

首先，程序需要识别一个图形是否为可镶嵌的四边形，如不是，则给出提示。该过程分为以下2 个部分。

第 1 步，识别待镶嵌的图形是否为四边形。CorelDraw 的图形以Bezier 曲线的形式表达，曲线在有尖角之处的节点左右两侧的切矢方向不同。程序以此作为四边形识别的依据：如果有尖角的节点数为4，则是四边形，否则不是。由于光滑曲线具有连续性特征，所有节点两侧的切矢方向均相同，所以该法可以同时用于检测直边四边形和曲边四边形。基于上述规则，三角形也可以用相同的技术来镶嵌，只要把2 个邻边做成一条直线即可。然而，由于检测规则的约束，2 条邻边的夹角不能是精确的180°，而应与180°保持1°以上的差值以确保图形被识别为四边形而非三角形，这个差值对四方连续图案的制作效果基本无影响。

第2 步，识别四边形是否可以镶嵌，直边四边形均可镶嵌，曲边四边形则需要满足边对称条件才能镶嵌。程序将四边形视为曲边四边形，并在相邻两尖角节点之间的曲线段上均匀取参数点，然后计算参数点到直边的距离（在直边一侧为正距离，另一侧为负距离），如果两侧对称位置的距离相等，则为可镶嵌四边形，见图8。

图8 识别四边形的可镶嵌性Fig.8 Judgment of quadrilateral's tessellability

3.4 复合单元的构建

本部分工作通过用户界面中的“复合单元构建”按钮完成。复合单元是指四边形（及其内部图形元素）通过复制、旋转、平移构成的复合无缝镶嵌单元，见图9。复合单元可以通过简单阵列形成四方连续，见图9a。

图9a 中：1 号单元为原始单元；2 号单元通过1号单元平移得到，平移向量为CA；3 号单元通过1号单元旋转180°，然后将旋转后的A 点与原B 点对齐得到；4 号单元通过1 号单元旋转180°，然后将旋转后的A 点与原D 点对齐得到。4 个四边形群组后得到一个复合单元，复合单元通过简单阵列即可得到四方连续图案。

图9 复合单元Fig.9 Composite unit

3.5 复合单元的阵列

本部分工作通过用户界面中的“复合单元阵列”按钮完成。对复合单元进行阵列的主要工作是确定2个方向（通常不是正交的）的复制向量，包括它的方向和长度2 个要素。复制向量通过对复合单元外轮廓上的角点进行计算得到。可以取图9a 复合单元外轮廓8 个节点中的2 个相对节点构建第1 个复制向量，如1、5 两点。另一复制向量由第1 个复制向量的2个节点号加2 得到，如1、5 节点对应的是3、7 节点。为了让2 个复制向量的方向尽量贴近两轴，在选择第1 对复制向量时会检测2 个节点连线与X轴方向的夹角，并取最小者确定复制向量。这样做是为了使生成的四方连续阵列尽量保持为一个矩形状态，以便最后使用一个矩形框来进行截取。将图9a 的复合单元原地复制后沿1、5 节点构成的向量连续平移可以得到一行单元，每行单元沿3、7 节点构成的向量进行连续复制可以得到多行单元，从而形成四方连续。

在选取第1 对复制向量时有可能遇到另一种情况，即2 个相对节点不是“腰点”（同时连接2 个四边形单元的节点，如1、3、5、7 节点），而是“角点”（只存在于1 个四边形单元中，如2、4、6、8 节点）。这种情况下，按照上述方案复制阵列会导致四方连续出现“中空”，即相邻单元以节点相连而非以边相连，类似菱形的常规二维阵列，因此需要在中空部位填补单元。可以利用程序来判断第1 对复制向量的2 个节点是否为腰点，不过为了简化代码，把这个工作留给了设计师，在界面上设置了一个“菱形”选项，用于处理复合单元菱形错行阵列的情况。“菱形”选项默认处于未选中状态，如果设计师发现复制向量属于第2 种情况，则将其选中，程序会自动在中空部位补充复制单元。

3.6 异质复合单元的构建

上述复合单元是由相同的原始单元组合而成，区别只有位置和角度不同。在复合单元的基础上可以发展出异质复合单元，即由不同的单元构成的复合单元。由于复合单元的可镶嵌性取决于其轮廓，所以可以通过打破内部边界的方式重新划分出不同的新单元形态，形成多种异质单元组合的镶嵌图案。如改变图9a 复合单元的4 条内部边界的形态，可以得到由4 个不同形状的四边形组合成的新复合单元，如图9b、图9c；或者取消复合单元的4 条内部边界，并连接3、7 两个节点形成新的内部边界，得到由2 个不同的五边形组合成的新复合单元。由于复合单元的内部边界可以任意划分，图案效果极具多样性，这也是Escher 镶嵌图形设计的重要原理之一。

图5b 用户界面的下端除了复合单元的构建和阵列外，还给出了一个正弦曲线的快速生成按钮，可以在2 点之间迅速创建一个周期的正弦曲线，图9b 中复合单元内部的重新分割就是利用2 条正弦曲线完成的。异质复合单元的镶嵌方式与同质复合单元的镶嵌方式相同。

4 案例应用验证与反思

4.1 案例应用验证

技术应用以纺织纹样中的一种常见四方连续形式为例进行设计。该四方连续由四色单元构成，4 种颜色的单元形态完全相同，只有方位不同，它们铺满整个空间，不留空隙。单元形态要求为具有一定复杂度的自由曲线形态，以避免单调。自由曲边四边形四方连续案例见图10。图10a 为基于图7 的自由曲边生成的自由曲边四边形，背后的细线是原始的直边四边形。图10b 为复合镶嵌单元。图10c 为基于复合单元生成的四方连续图案。

图10 自由曲边四边形四方连续案例Fig.10 Example of free curve-edge quadrilateral tessellation

可以看到，文中的方法可以简单、快捷地实现基于复杂单元图形的四方连续图案设计，图案单元嵌合精确、细节丰富，并且在单元设计环节给设计师留出了充分的创意发挥空间。所开发的工具软件，可以让智能技术和设计师共同协作并高效完成四方连续的创意设计工作。

4.2 反思

文中的技术在智能化方面还有进一步提升的空间，主要如下：基于智能化手段的自由曲边的形态设计，特别是带有某些具象特征的曲线形态，如传统纹样图形元素面向可镶嵌的图形单元的定制设计，可以让传统纹样的应用不再是简单的阵列，而是带有一些理性的几何逻辑，对传统文化的创新也有促进作用；基于优化算法的曲边交叠性校验与修正，设计自由曲边四边形时，曲边之间有可能产生交叠，影响单元的可镶嵌性，因此可将曲线定义为参数化曲线，使用交互式遗传算法等智能优化工具来搜寻无交叠的最优解；对设计师手绘图案的智能识别机制，基于智能化技术对设计师手工制作的图形的不规范之处逐一进行鉴别并处理，以减少设计师在琐碎事务上耗费的精力。

5 结语

基于四边形镶嵌的四方连续图案生成方法在原理上早已成熟。尽管如此，手工绘制镶嵌单元图形仍是一项复杂的工作。文中所开发的技术主要贡献有如下几点：基于通用平面设计软件平台开发了专用工具，并实现了智能镶嵌设计；利用四边形镶嵌作为空间填充布置的工具，实现了丰富、复杂的连续图案设计效果，为面向空间充分利用的排版设计提供了一种通过设计师输入参数进行驱动设计的方便工具；通过程序保证曲边四边形的可镶嵌性条件，让设计师可以利用手绘的自由曲线来迅速生成无缝镶嵌图案单元；通过复合单元的重构，可以生成异质单元的无缝镶嵌图案；基于选定的图形单元，可以构造出可镶嵌四边形或复合单元。

事实上，理论界和技术界的很多研究仅止步于算法，应用层面的创新探索还远远不足，在服务生产方面也有大量的开发工作有待落实，这中间的断层是设计类研究创造价值的聚集地，也是通过大量实践和迭代发现新的科学问题的契机。