平纹编织复合材料层合板静态压缩与压-压疲劳性能

张铁纯, 杨晨晨, 王 轩, 周春苹

（1．中国民航大学 航空工程学院, 天津 300300；2．航空工业济南特种结构研究所 高性能电磁窗航空科技重点实验室, 济南250023）

玻璃纤维平纹编织复合材料具有轻质、比强度和比刚度高、透波性好等优点，被广泛应用于航空航天领域，如机载雷达罩、整流罩等部位[1]。这些结构部位主要受变化的局部空气动力载荷作用，经常处于压-压交变受力状态。因此，系统研究玻璃纤维平纹编织复合材料的压-压疲劳性能，了解其疲劳损伤规律，对于玻璃纤维平纹编织复合材料在航空航天领域的进一步应用尤为重要。

目前，Wang 等[2]研究了玻璃纤维环氧树脂基复合材料的拉-拉疲劳行为，揭示了不同应力水平下复合材料的疲劳损伤机理。Singh 等[3]对玻璃纤维增强树脂基复合材料层合板在[0o/90o]、[±15o]、[±30o]和[±45o]铺层角度下进行拉-拉疲劳研究，结果表明：铺层取向对疲劳失效模式有显著影响；疲劳载荷作用下刚度呈现3 阶段衰退规律。Zhang 等[4]提出了纤维增强复合材料的疲劳损伤模型，该模型描述了不同应力比下任意纤维取向的离轴单向纤维增强复合材料层合板的疲劳损伤累积和疲劳寿命。Movahedi-Rad 等[5]研究了玻璃纤维环氧树脂基复合材料层合板的拉-拉疲劳行为，发现在高应力水平下，试件在较短的寿命内发生纤维拔出失效；由于无界区域大的摩擦，能量耗散随着循环次数和疲劳应力水平的增加而增加。Brunbauer等[6]研究了纤维体积分数对玻璃纤维增强树脂基复合材料疲劳损伤机制的影响，发现纤维体积分数不会显著影响拉-压疲劳实验中的疲劳强度。Manjunatha 等[7]对玻璃纤维混合环氧树脂和纯环氧树脂两种复合材料分别进行了拉-拉疲劳实验，结果发现混合环氧树脂复合材料疲劳寿命比纯环氧树脂复合材料高6～10 倍。Malpot等[8]研究了玻璃纤维平纹编织复合材料的拉-拉疲劳性能，利用S-N曲线评估了三种疲劳寿命模型的材料参数，通过扫描电子显微镜观察到纤维基体脱粘、富脂区基体裂纹和分层现象。Vieille 等[9]在高于玻璃化转变温度的温度下，研究了塑性和黏性效应对纤维增强复合材料层压板拉-拉疲劳行为的影响。Liu 等[10]对玻璃纤维增强树脂基复合材料进行了拉-拉疲劳实验研究，利用不同预测模型对玻璃纤维增强树脂基复合材料疲劳寿命进行建模，结果表明实验数据与指定参数的模型吻合较好。郭霞等[11]通过对复合材料胶接结构的拉-拉疲劳特性进行实验研究，采用载荷-寿命曲线疲劳寿命预测方法拟合得到疲劳寿命预测模型。程小全等[12]研究了纤维增强复合材料疲劳寿命预测及损伤分析模型，讨论了疲劳寿命模型、唯象模型和渐进损伤模型的发展趋势。陈基伟等[13]针对纤维增强树脂基复合材料提出了一种剩余刚度概率模型，所提出的模型可以较好地描述实验结果。李鹏扬等[14]建立了能准确描述拉-拉疲劳载荷下复合材料的塑性变形能与材料发热所消耗的耗散能之和的量化模型，通过疲劳实验对所建立模型的合理性进行验证。Keller 等[15]研究了载荷中断对玻璃纤维环氧树脂基复合材料层合板拉-拉疲劳行为的影响，通过施加间断疲劳载荷，每次加载中断后，由于黏弹性聚合物基体的恢复，刚度部分恢复，每次加载模块开始时重复的材料硬化延迟了裂纹的扩展，裂纹钝化进一步延迟了损伤增长，增加了材料的损伤累积能力，间断疲劳加载的试件与连续加载的试件相比表现出更长的疲劳寿命。

分析上述文献可知，平纹编织复合材料层合板压-压疲劳研究较少，主要原因是目前国内外还缺少统一的层合板压-压疲劳实验标准。本工作基于ASTM 层合板静态压缩标准开展玻璃纤维平纹编织复合材料层合板静态压缩性能和压-压疲劳性能实验研究，考虑不同峰值载荷下的疲劳行为，分析疲劳过程中玻璃纤维平纹编织复合材料的刚度退化、能量耗散、循环蠕变与循环软化，结合扫描电子显微镜对试件断口形貌进行观察，揭示其在静态压缩载荷与循环载荷作用下的损伤演化机理。

1 实验方法

参考ASTM D-6641/D-6641M-09 标准，对玻璃纤维平纹编织复合材料层合板进行静态压缩和压-压疲劳性能测试，试件采用7781 E 型玻璃纤维预浸料和3M PR381 环氧树脂制成，尺寸和形状如图1 所示。静态压缩与压-压疲劳实验在Instron 8801 电液伺服疲劳试验机上完成，实验矩阵如表1 所示。静态测试加载速度为1.2 mm•min-1。疲劳测试选取应力比R=10，最大应力循环周次为106，采用应力控制加载，加载频率为4 Hz，波形为正弦波，采用8 级载荷水平进行S-N曲线测试，实验环境为室温、干态。采用S-3400N 扫描电子显微镜对试件断口进行微观形貌分析。

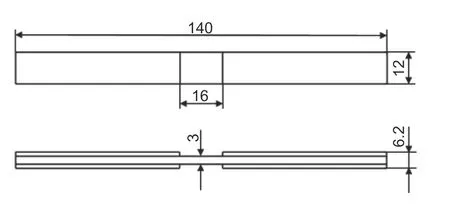
图1 试件尺寸和形状Fig. 1 Size and shape of test piece

表1 实验矩阵Table 1 Experimental matrix

2 结果分析与讨论

2.1 静态压缩强度

静态压缩实验结果如表2 所示。由表2 可以看出，玻璃纤维平纹编织复合材料层合板平均压缩强度σa为357.83 MPa，压缩强度变异系数为2.7%，在工程的可接受范围内。

表2 静态压缩实验结果Table 2 Static compression test results

2.2 失效模式

图2 为试件失效模式。从图2 可以看出，静态压缩（图2（a））失效模式属于ASTM 标准试件（图2（b））可接受的失效模式中的一种，说明静态压缩实验的有效性。疲劳试件（图2（c））具有与静态压缩试件（图2（a））相同的失效模式。

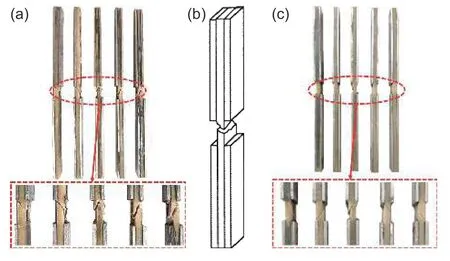
图2 试件失效模式 （a）静态压缩；（b）ASTM 标准；（c）压-压疲劳Fig. 2 Failure modes of specimens （a）static compression；（b）ASTM standard；（c）compression-compression fatigue

2.3 S-N曲线

压-压疲劳实验结果如表3 所示。S-N曲线由不同载荷水平下疲劳测试得到。其中，条件疲劳极限利用升降法获得，采用成组法描述S-N曲线有限寿命区[16]。表3 中，试件编号为P-1 和P-2 两个试件用来确定升降法中第一个有效数据。试件编号为P-3 至P-15 共13 个数据为升降法获得的有效数据，根据式（1）来确定条件疲劳极限。

表3 压-压疲劳实验结果Table 3 Compression-compression fatigue test results

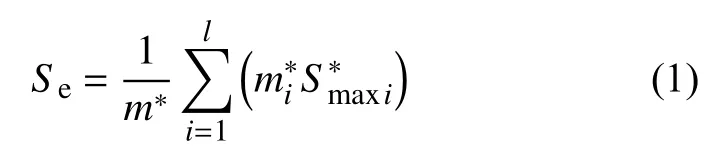
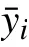
图3 确定条件疲劳极限的升降图Fig. 3 Lifting figure for determining conditional fatigue limit

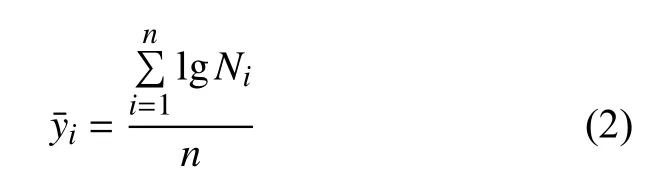
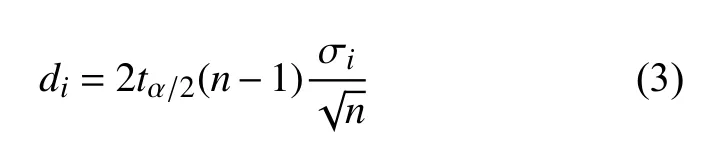
N(Smax−S0)H=C(4)

式中：S0为理论疲劳极限；H、C为待定常数；Smax为峰值应力；N为疲劳寿命。

图4 为采用双加权最小二乘法拟合的S-N曲 线。计 算 得 到H=0.781，C=2.92415×105，S0=237.64 MPa。可以看出，拟合的S-N曲线通过了疲劳实验数据的95%置信区间，因而具有较高的可信度。拟合的S-N曲线获得的疲劳极限与通过升降法获得的疲劳极限大小相差0.26%。

图4 玻璃纤维平纹编织复合材料层合板S-N曲线Fig. 4S-Ncurve of glass fiber plain woven composite lamin ates

2.4 刚度退化与能量耗散

采用迟滞回线割线模量来表征试件在循环载荷作用下的刚度变化，每个循环周期的迟滞回线面积大小代表该循环周期能量耗散大小。典型迟滞回线相关定义如图5 所示。图6 分别给出了-10 kN和-8.4 kN 峰值载荷作用下，试件在不同循环次数下的迟滞回线示意图。从图6 可以看出，随着循环次数的增加，迟滞回线发生了移动。在循环载荷作用下，试件产生的永久性损伤或塑性变形导致迟滞回线发生移动[3]。另外，试件迟滞回线的割线模量逐渐减小。其他峰值载荷下的试件迟滞行为相似。

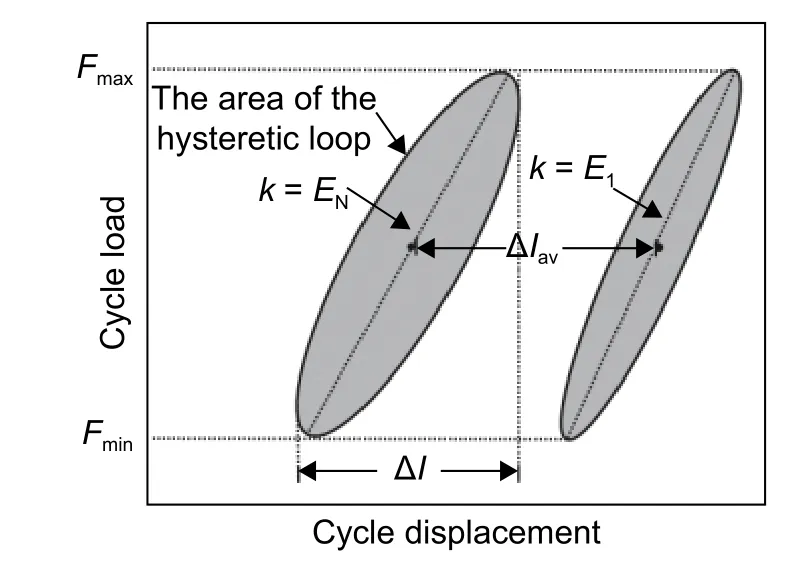
图5 典型迟滞回线相关定义Fig. 5 Typical hysteresis loop related definition

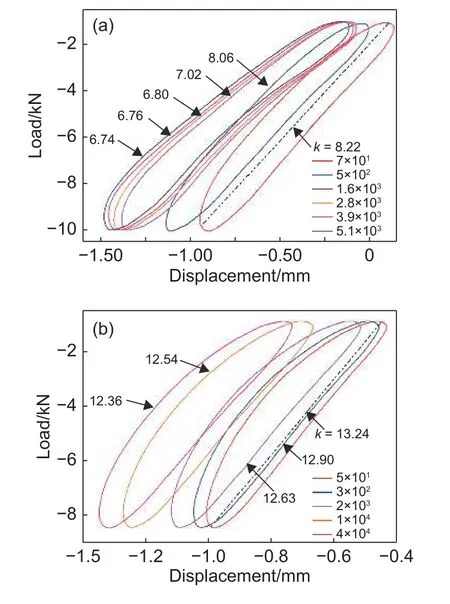
图6 不同循环次数下迟滞回线示意图 （a）-10 kN 峰值载荷；（b）-8.4 kN 峰值载荷Fig. 6 Schematic diagram of hysteresis loops with different cycles （a）-10 kN peak load；（b）-8.4 kN peak load

图7 为各峰值载荷作用下试件由第一个循环周期的刚度E1归一化的疲劳刚度EN/E1与归一化疲劳寿命N/Nf的关系，横坐标中的N为当前循环寿命，Nf为疲劳寿命。从图7 可以看出，无论峰值载荷多大，刚度退化都遵循相似的模式。在疲劳寿命的前10%期间，刚度急剧下降，且高峰值载荷下的刚度下降幅度较大，低峰值载荷下的刚度下降幅度较小；疲劳寿命的20%以后刚度下降幅度很小，直至所有试件发生失效。在循环加载初期，刚度的显著变化归因于试件早期更大的损伤形成和增长[5]。

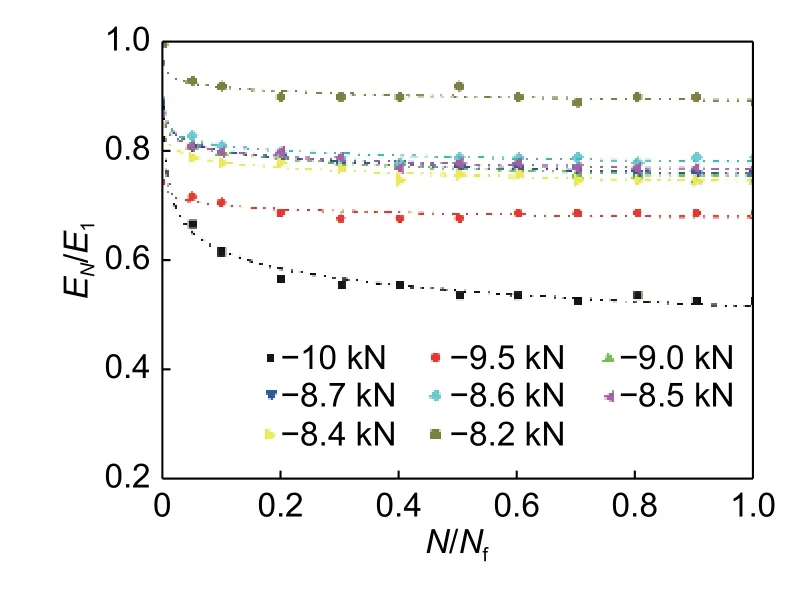
图7 不同峰值载荷作用下归一化疲劳刚度EN/E1与归一化疲劳寿命N/Nf的关系Fig. 7 Curves ofEN/E1（normalized fatigue stiffness）vs N/Nf（normalized fatigue life） under different peak loads

图8 为不同峰值载荷作用下试件在第一次循环、25%、50%、75%循环次数和最后一次循环下的迟滞能量耗散。由图8 不难发现，随着循环次数的增加，各峰值载荷下的能量耗散逐渐增加，即迟滞回线面积逐渐增加，这主要因为损伤的增长使得试件内部摩擦增加，进而导致热能耗散增加[18]。Meneghetti 等[19]在对玻璃纤维增强聚丙烯复合材料进行拉-压疲劳研究时，也发现能量耗散随着循环次数的增加而增加。摩擦的大小取决于裂纹尺寸大小，随着循环次数的增加和高峰值载荷作用，裂纹尺寸更大。此外，试件内部裂纹间的内耗也会引起能量耗散[5]。在疲劳寿命的前25%，各峰值载荷下的能量耗散增加幅度较大。而在此之后的寿命中，能量耗散增加幅度较缓慢。与其他峰值载荷作用下相比，低峰值载荷作用下的试件在疲劳寿命的前25%，能量耗散增加幅度较小。

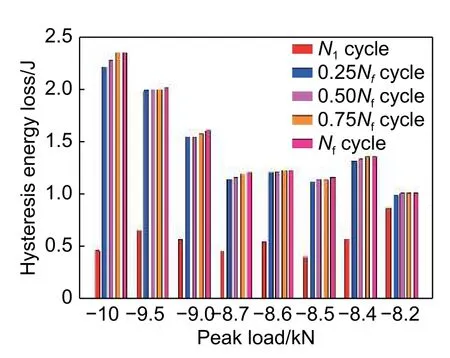
图8 不同峰值载荷作用下试件在不同循环次数下的迟滞能量耗散Fig. 8 Hysteretic energy loss of test piece under different peak loads and different cycle numbers

2.5 循环蠕变与循环软化

从图6 可以看出，随着循环次数的增加，试件的迟滞回线发生了移动。图9 为不同峰值载荷作用下试件第一次平均循环位移和当前平均循环位移的差值Δlav与归一化疲劳寿命N/Nf的变化关系。正如图9 所观察到的，无论峰值载荷多大，Δlav变化都遵循相似的模式。在疲劳寿命的前20%期间，Δlav急剧增加，这说明在循环初期，迟滞回线发生了移动，且移动幅度较大，试件表现出强烈的循环蠕变现象，随后逐渐减弱，并趋于稳定。循环初期试件的损伤或塑性变形导致迟滞回线发生移动[3]。此外，随着循环次数的增加，-10 kN、-9.5 kN 峰值载荷作用下的试件表现出大的平均循环位移。由于基体的黏弹性变形，高峰值载荷作用下的试件表现出明显的循环蠕变现象[5]。

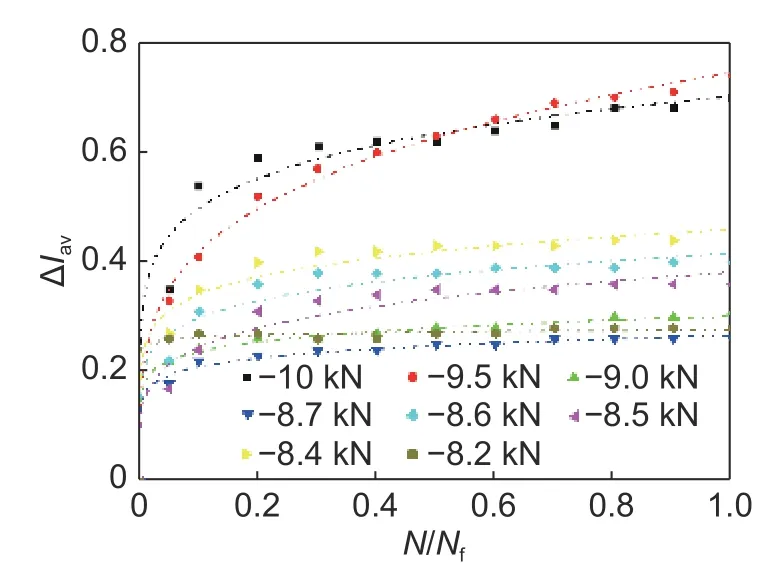
图9 不同峰值载荷作用下Δlav（第一次平均循环位移和当前平均循环位移的差值）与N/Nf（归一化疲劳寿命）的关系曲线Fig. 9 Curves of Δlav（difference between the first average cyclic displacement and the current average cyclic displacement）vs N/Nf（normalized fatigue life）under different peak loads

图10 为不同峰值载荷作用下试件同一循环最大循环位移与最小循环位移的差值Δl与初期循环寿命（前250 次）的变化关系。从图10 可以看出，不同峰值载荷作用下，循环初期试件的循环位移不断增加，即存在循环软化行为，高峰值载荷作用下的试件循环软化行为表现得比较强烈，低峰值载荷作用下的试件循环软化行为表现得不明显，随着循环次数的增加，试件的循环软化行为逐渐减弱，并趋于稳定。

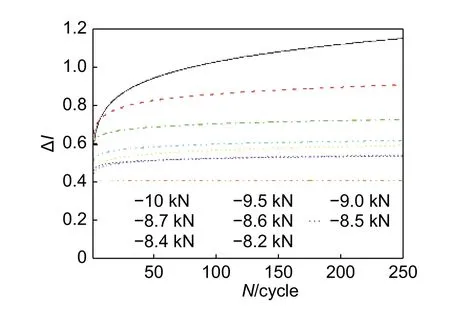
图10 不同峰值载荷作用下试件同一循环最大循环位移与最小循环位移的差值Δl与初期循环寿命N的关系Fig. 10 Curves of Δl（difference between the maximum and minimum cyclic displacements of the same cycle）vs N（the initial cycle life）under different peak loads

2.6 剩余载荷

对达到最大应力循环周次（106）的试件（P-4、P-5、P-6、P-8、P-9、P-14、P-15），进行剩余载荷测试，结果见表3。图11 为试件静态压缩载荷-位移曲线与疲劳测试后剩余载荷-位移曲线对比图。从图11 可以看出，试件剩余载荷-位移曲线线性段的斜率明显大于静态压缩载荷-位移曲线线性段斜率。这表明试件经过循环载荷作用后抵抗变形能力得到了增强。试件经过循环载荷作用达到最大应力循环周次后，疲劳实验停止，由于短暂的停止，损坏的黏弹性基体导致裂纹钝化，裂纹尖端开裂区的局部应力强度显著降低[15]，从而延迟了裂纹扩展。再次进行剩余载荷测试时，增加了材料的断裂韧度[20-22]。材料断裂韧度的增加和裂纹钝化，使得刚度退化显著延迟，损伤累积能力增加[15]。这就是试件剩余载荷-位移曲线线性段的斜率大于静态压缩载荷-位移曲线线性段斜率的原因。图12 为不同加载条件下的破坏位移分布。从图12 可以看出，循环载荷下的破坏位移远小于静态压缩载荷下的破坏位移，循环加载后试件的剩余载荷略高于静态极限载荷。剩余载荷下的破坏位移略低于静态极限载荷下的破坏位移。由于循环加载后部分试件的剩余载荷与静态极限载荷相接近，当加载到极限载荷时，经过循环加载试件抵抗变形能力提高，对应剩余载荷下的破坏位移小于静态极限载荷下的破坏位移。

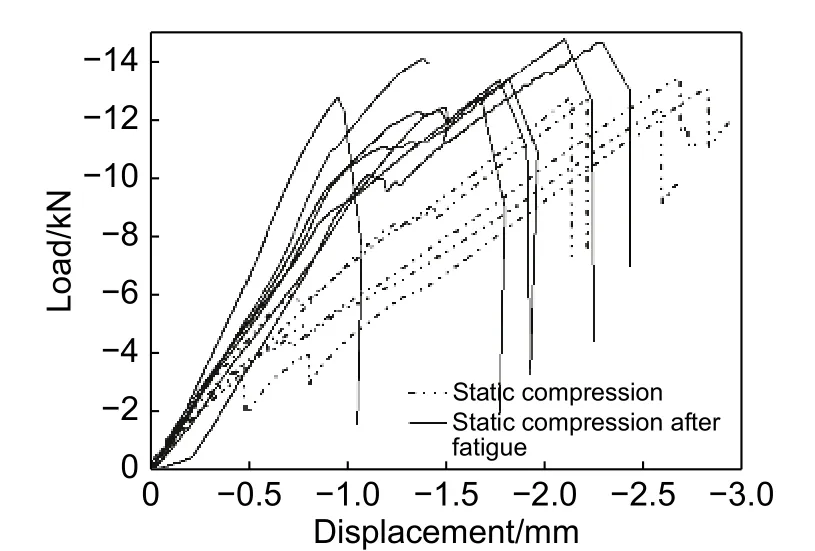
图11 载荷-位移曲线Fig. 11 Load-displacement curves

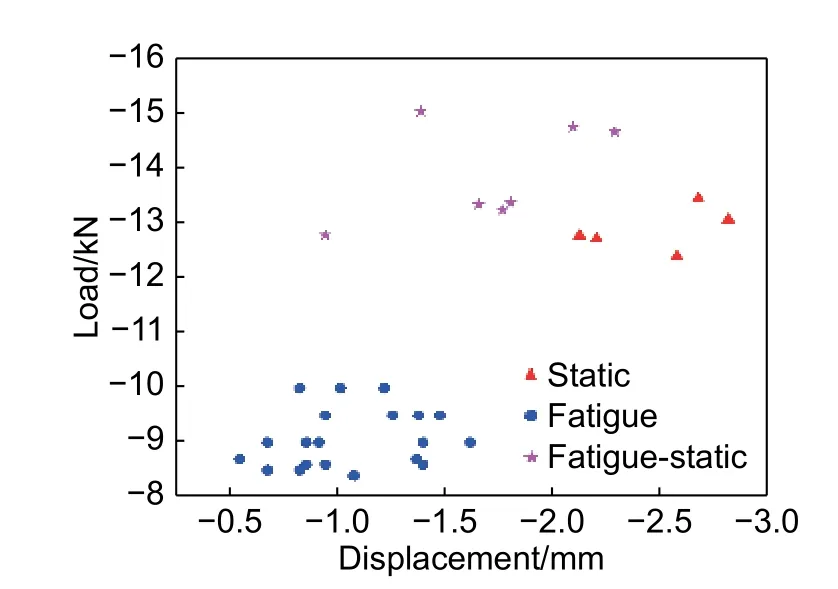
图12 不同加载条件下的破坏位移Fig. 12 Failure displacements under different loading condi tions

2.7 断口形貌

图13 和图14 为试件断口微观组织形貌扫描电镜照片。其中图13（a）～（f）为静态压缩试件断口形貌；图14（a）和（b）为试件在-8.5 kN 峰值载荷作用下循环85899 次发生疲劳破坏后的断口形貌；图14（c）和（d）为剩余载荷试件的断口形貌；图14（e）和14（f）是试件在-9.0 kN 峰值载荷作用下循环714239 次发生疲劳破坏后的断口形貌。可以看出，静态压缩断口（图13（a））与疲劳断口（图14（a））可清晰观察到纤维被拉出，当裂纹扩展时，纤维和基体之间强黏附性导致纤维的更多损伤[23]。另外，纤维断裂的横截面是平的，可以证明玻璃纤维断裂为脆性断裂。静态压缩断口（图13（d））与剩余载荷试件断口（图14（c））中存在纤维的明显剥离，裂纹扩展引起的张力使得纤维发生破坏，产生许多碎片纤维。由于良好的黏附性而存在更多碎片纤维，意味着更多的能量被纤维吸收[23]。图13（b）和（c）中可清晰地观察到纤维/基体界面脱粘现象，图14（b）也观察到了这一现象。图13（e）为环氧树脂的断裂表面，可明显看到基体开裂现象，疲劳断口（图14（b））也发现了基体开裂现象。当循环载荷峰值低于疲劳极限时，沿载荷方向在纤维束之间形成微裂纹，产生大量拉脱松散的纤维（图14（d）），随着循环次数的增加，试件断口表面呈现为带有损伤纤维的块状图案（图14（d））。这表明，循环载荷会在纤维与基体之间的界面上形成微裂纹，当界面强度在循环加载降低时，材料结构发生显著变化，纤维发生断裂[24]。此外，静态压缩断口（图13（f））与疲劳断口（图14（e）和（f））还观察到了明显的分层损伤，与疲劳断口相比，静态压缩断口表现出较大的分层损伤。

图13 静态压缩试件断口形貌 （a）纤维拉出；（b）、（c）纤维/基体脱粘；（d）纤维脱落；（e）基体开裂；（f）分层Fig. 13 Fracture morphologies of static compression test pieces （a）fiber pull-out；（b），（c）fiber/matrix debonding；（d）fiber peeling；（e）matrix cracking；（f）delamination

图14 疲劳试件断口形貌 （a）纤维拉出；（b）纤维/基体脱粘、基体开裂；（c）纤维脱落；（d）松散的纤维；（e）、（f）分层Fig. 14 Fracture morphologies of fatigue test pieces （a）fiber pull-out；（b）fiber/matrix debonding，matrix cracking；（c）fiber peeling；（d）loose fibers；（e），（f）delamination

3 结论

（1）试件条件疲劳极限为平均静态压缩强度的66.3%。随着循环次数的增加，层合板刚度逐渐下降，在寿命的前10%期间，刚度急剧下降，且高峰值载荷作用下，刚度下降幅度较大，低峰值载荷作用下，刚度下降幅度较小。

（2）随着循环次数的增加，各峰值载荷下的能量耗散逐渐增加；在寿命的前25%，各峰值载荷下的能量耗散增加幅度较大。而在此之后的寿命中，能量耗散增加幅度较缓慢。

（3）在循环加载初期，无论峰值载荷多大，层合板都表现出强烈的循环蠕变现象；高峰值载荷作用下，层合板表现出强烈的循环软化行为，随着循环次数增加，层合板循环软化行为逐渐减弱，并趋于稳定。

（4）经过循环加载层合板抵抗变形能力得到了增强。层合板断口观察到了基体开裂、纤维/基体界面脱粘、纤维断裂和分层四种失效模式。与疲劳断口相比，静态压缩断口表现出较大的分层损伤。