基于双射角射线扫描的平面定位研究

李立新，丁电宽，冯丽娜

(安阳师范学院 物理与电气工程学院，河南 安阳 455000)

0 引言

自动作业系统中，对工作区内作业对象的定位是自动控制系统中的必要环节[1]。利用特定双直角三角形斜边相交[2]，求解交点到直角边距离的几何原理，用双射角射线扫描可以实现对平面工作区内随机位置物体的纵横双向定位。其精简扫描模式和最优扫描模式适用于长阵列红外扫描汽车定位系统[3]，实际应用中可替代、优化原有的红外扫描与超声波测距组合平面定位系统。

1 双射角射线扫描平面定位

1.1 双射角平面定位数学模型

如图1所示，Rt△A1B1C1和Rt△A2B2C2，∠A1B1C1=∠A2B2C2=90°，∠B1A1C1=α1，∠B2A2C2=α2，且α1>α2，α2≥0，两条直角边B1C1和B2C2处于同一条直线上，另外两条直角边A1B1=A2B2，两条斜边相交于P，若已知B1B2间距，则P到各直角边的距离可以通过下面方法求出。

图1 双射角平面定位数学模型

作三条辅助线，一条是A1E，A1E平行于A2C2，即∠B1A1E=α2，第二条是PD1，PD1⊥A1B1，交A2B2于D2，第三条是PF，PF⊥B1C1。PD1、PD2、PF就是P到各直角边的距离。

因△EA1C1与△C2PC1为相似三角形，所以

(1)

又因△A1B1C1与△PFC1为相似三角形，所以

(2)

由式(1)和式(2)得

故P到直角边B1C1和B2C2的距离

(3)

由式(2)得

故P到直角边A1B1的距离

(4)

故P到直角边A2B2的距离

(5)

将△A1B1C1和△A2B2C2，置于平面直角坐标系中，如图1所示，B1在横轴上的坐标用XB1表示，则P点坐标(XP，YP)可表示如下：

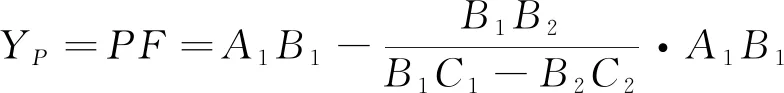
(6)

1.2 双射角射线扫描平面定位测量算法

如图2所示，有矩形工作区，宽为H，长为L。在工作区随意放置一长方形实物P，基于双射角平面定位数学模型，可用双射角射线扫描定位测量P的四个顶角坐标。

图2 双射角扫描平面定位测量

先以P1顶角为例说明。将上侧边线和下侧边线按单位长度ΔL均匀划设N个刻度，刻度值用n表示，其中ΔL=L/N，n=0～N。将左边线和右边线按单位长度ΔL均匀划设I个刻度，刻度值用i表示，其中ΔL=H/I，i=0～I。

在上边线n位置放置一个射线发射器，在下边线n+m1位置放置一个射线接收器，即接收器位置在X轴正方向超前发射器m1刻度，构成射角为α1的射线测量组(以下简称α1测量组)，其中tanα1=m1/I。发射器上边线从刻度0向N逐步移动，接收器在下边线也同时从刻度m1向N方向移动，每次移动一个刻度，两者同步移动，保持射角α1不变。当接收器从刻度m1移动至N时，α1测量组完成一次工作区扫描。在α1测量组扫描工作区时，射线在P1点处形成通断转换，断点位置标记为n1/(n1+m1)，即断点发射器位置n1，接收器位置n1+m1。

再以α2测量组(接收器位置在X轴正方向超前发射器m2刻度，tanα2=m2/I)对工作区进行扫描，射线在P1点处形成通断转换，断点位置标记为n2/(n2+m2)，即断点发射器位置n2，接收器位置n2+m2。在α1>α2，α2≥0时，根据式(6)可得P1在平面直角坐标系中的坐标(x1，y1)为：

(7)

α1测量组和α2测量组在扫描经过P2点时，再次形成通断转换，断点位置分别标记为n3/(n3+m1)和n4/(n4+m2)，同理可得P2在平面直角坐标系中的坐标(x2，y2)为：

(8)

由于α1测量组和α2测量组在扫描经过P3、P4点时，射线无法形成通断转换，需要改变射角方向进行扫描。如图3所示，把射角分为前射角和后射角两种，接收器位置在X轴正方向超前发射器位置的称为前射角，接收器位置在X轴正方向滞后发射器位置的称为后射角。P1、P2定位用的是前射角扫描，α1测量组和α2测量组可进一步改称为前α1测量组和前α2测量组，P3、P4定位需要用后射角扫描，测量组称为后α1测量组和后α2测量组。

图3 前射角与后射角示意图

如图4所示，后α1测量组和后α2测量组在扫描经过P3点时，射线形成通断转换，断点位置分别标记为n5/(n5-m1)和n6/(n6-m2)，同理可得P3在平面直角坐标系中的坐标(x3，y3)为：

图4 后射角双射角扫描平面定位测量

(9)

后α1测量组和后α2测量组在扫描经过P4点时，射线形成通断转换，断点位置分别标记为n7/(n7-m1)和n8/(n8-m2)，同理可得P4在平面直角坐标系中的坐标(x4，y4)为：

(10)

2 测量结果分析

2.1 纵向测量结果分析

先分析P1点纵坐标y1。式(7)中，n2-n1是双射角扫描断点发射器位置间距，m1-m2与α1、α2角度取值有关，令Δn1=n2-n1，ΔM=m1-m2。为此，P1点纵坐标y1可以表示为：

由上式可知，y1测量结果与双射角扫描断点相对位置有关。两个断点发射器位置间距Δn1越小y1越大；反之，Δn1越大y1越小。因0≤Δn1≤ΔM，所以，当Δn1=ΔM，即断点发射器位置间距最大时，y1=0，为最小值。而当Δn1=0，即断点发射器位置间距最小时，y1=I，为最大值。

由上式还可知，y1的最小变化量是I/ΔM,即纵向测量结果分辨力为I/ΔM*ΔL。当I/ΔM>1时，纵向测量结果分辨力大于ΔL；当I/ΔM=1时，纵向测量结果分辨力等于ΔL；当I/ΔM<1时，纵向测量结果分辨力小于ΔL。即减小I/ΔM可以优化纵向测量结果分辨力。

图5 断点位置误差示意图

因-1<Δl2-Δl1<1，所以-I/ΔM<Δy1

由此可见，纵向测量结果最大误差不超过I/ΔM*ΔL，即纵向测量精度为±I/ΔM*ΔL。当I/ΔM<1时，纵向测量结果最大误差小于ΔL；当I/ΔM=1时，纵向测量结果最大误差等于ΔL；当I/ΔM>1时，纵向测量结果最大误差大于ΔL。即减小I/ΔM可以优化纵向测量精度。

2.2 横向测量结果分析

再来分析P1点横坐标x1。同上，x1可以用下式表示：

由上式可知，x1测量结果与双射角扫描断点位置以及两断点相对位置有关。x1等于断点发射器位置n1以及该断点发射器位置与P1点之间的横向间距两者之和。

如图5所示，同样因扫描移动步长为ΔL，导致实际断点与测量断点位置存在误差，影响横向测量结果x1。若用Δx1表示P1点横向坐标测量误差，则P1点实际的横向坐标x1S为：

图6表示出Δx1与Δl1、Δl2、m1/ΔM之间的关系。m1/ΔM越小，误差范围越小。由于m1/ΔM≥1，当达到最小值m1/ΔM=1时，误差范围最小，且误差大小与Δl1无关；当m1/ΔM>1时，Δl1越大，误差范围正向极值越大，Δl2越大，误差范围负向极值越大。

图6 Δx1与Δl1、Δl2、m1/ΔM之间的关系

2.3 测量优化措施分析

2.3.1 双射角的选择

减小I/ΔM可以优化纵向测量精度，减小m1/ΔM可以优化横向的测量误差范围。因为

所以，双射角的选择关系到测量结果的质量。

发射角α2的选择。由上式可知，减小tanα2是优化措施之一。但0≤tanα2<∞，故tanα2=0，即α2=0是极限选择。当α2=0时，前α2测量组和后α2测量组合二为一，称之为精简扫描模式。这种极限选择仅限于实物P左右侧边垂直于测量上下区边线的情况，其他情况下，要保证α2不小于实物P左右侧边倾角。

发射角α1的选择。由上式可知，增大tanα1是优化措施之一。为了保障工作区为有效测量区，双射角定位测量需要在工作区前后增加附加测量区，tanα1增大会增加附加测量区长度。为兼顾尽量减小附加测量区长度和测量结果尽量优化，一般选择tanα1=1，即α1=45°为宜。

若选取α2=0和α1=45°，扫描精简，且Δx1误差范围最小，Δy1测量精度较好，称之为最优扫描模式。

2.3.2 单位长度ΔL的选择

双射角断点位置误差Δl1和Δl2是形成定位测量误差的主要原因。Δl1和Δl2的长度最大值小于一个单位长度ΔL，所以，减小单位长度ΔL的值是提高定位测量精度的重要措施。一般情况下，单位长度ΔL应小于设定的测量精度值。

2.3.3 平移修正算法优化

由于n1′位于n1与n1-1之间，n2′位于n2与n2-1之间，0≤Δl1<1,0≤Δl2<1。若在计算时对n1与n2做-0.5平移修正，即将断点和相邻通点的中间点作为修正测量断点，则进行修正后有-0.5≤Δl1<0.5,-0.5≤Δl2<0.5。表1对比了修正前后Δx1误差范围，平移修正后Δx1误差范围得以优化，最大误差减小。平移修正算法对Δy1没有改善作用。

表1 平移修正前后误差对比表

P2、P3、P4分析结果与P1相同，不再论述。

3 在长阵列扫描定位系统中的应用

长阵列红外扫描定位系统是车载物料作业系统中自动控制系统的重要组成部分，用于对平面内汽车位置进行检测。如图7所示，该系统由红外发射阵列和红外接收阵列组成，有N个发射模块和N个接收模块，相邻模块间隔ΔL，收发模块一一位置对应，在扫描移位脉冲的作用下，可以控制逐对轮流接通。采用发射模块接收模块错位组合扫描[4]，可以按照双射角定位算法完成对汽车位置的定位。

在该系统中，由于车辆进入工作区前经过引道，车厢侧边与工作区横向中线基本平行，适用于精简扫描模式。在车厢后面有较为充裕的空间，可以对车尾两角采用最优扫描模式。在拖挂车情况下，拖车挂车间距不同，需根据实际调节发射角。一般采用三轮扫描，第一轮采用零射角扫描(逐位移动对位扫描)，确定车厢横坐标位置xP1(xP3)、xP2(xP4)、xP5(xP6)等。第二轮、第三轮采用错位扫描，分段采用不同射角。第二轮首先是前射角α1扫描，之后结合接收和发射交替脉动移位，转换为后射角α2→α2+变角扫描等，依次确定yP1、yP4、yP5等坐标。第三轮首先是后射角α1扫描，之后结合发射和接收交替脉动移位，转换为前射角α3→α3+变角扫描，依次确定yP3、yP2、yP6等坐标。车尾处采用射角α1=45°，拖车挂车间采用的射角大小依据第一轮扫描测得的拖车挂车间距以及之前射角α1扫描测得的车尾角纵坐标来动态确定。根据三轮扫描结果计算出车辆位置。实测结果，车厢横向位置误差小于1/2ΔL，车尾两角位置纵向误差小于ΔL，综合定位结果达到红外扫描与超声波测距组合定位水平。

4 结论

基于双射角扫描的平面定位方法，利用特定双直角三角形几何特性，结合射线扫描，对指定区域的物体进行纵横双向定位，具有可行性。该方法对纵向位置测量时，受限于附加测量区长度和光源器件半角值等因素，射角一般难以超过45°，所以纵向位置测量精度通常不及横向位置测量精度。研究以矩形工作区、长方形实物为背景讨论了双射角扫描平面定位算法，对于非矩形工作区、其他多边形物体，也可以以此为基础，经过算法处理完成定位。