双层非负矩阵分解的分形图像压缩算法

方美东，王 辉，张爱华

南京邮电大学 理学院，南京 210023

如果一个对象的部分与整体以某种规则联系起来，通过某种变换使之对应，那么可将它看成分形。自1988年Barnsley首次提出分形图像压缩编码的概念以来，分形图像压缩编码已获得广泛认可[1-2]，并成为近年来最受欢迎的现代图像压缩方法之一[3]。之后，基于块的分形图像编码方法被Jacquin[4]和Barnsley[5]提出。分形块编码方法[6]是在自然图像具有丰富仿射冗余的情况下，发现一个构造规则来构造近似图像。

分形图像压缩将图像分成Range块和Domain块，然后在Domain块池中搜索与之最佳匹配的Range块。该方法在编码过程中只记录匹配过程中必要的变换参数[7-9]。在分形图像压缩过程中，关键性问题是如何优化匹配方案，减少压缩时间，提高重建图像的质量。Huang等[10]提出了一种基于分形特征的图像检索方法。

NMF本质上是一种无监督的特征提取算法，其思想最早可追溯到Paatero等[11]在1994年提出的正矩阵分解的概念。Lee和Seung于1999年在Nature上正式提出了NMF方法和概念[12]。近年来，NMF在人脸识别[13-15]及特征提取[16]等领域得到广泛应用。

NMF收敛效果不够明显，Hoyer首次提出将稀疏约束的思想加入NMF[17]，接着Hoyer提出了一种介于L1范数和L2范数之间的稀疏度量[18]；Du等提出了L3/2范数的稀疏约束NMF[19]和基于L3/2范数的图正则NMF[20]；Yang等在NMF基础上增加了投影约束限制[21]。本文在投影非负矩阵分解的基础上加入L3/2范数的稀疏约束，构建了双层非负矩阵分解，提取图像的稀疏特征灰度值，然后对特征进行K-means聚类，接着进行基于分类下的稀疏分解，相较于其他算法，本文改进算法在分形图像压缩的过程中提高了重建图像的效率。

1 理论基础

1.1 非负矩阵分解

非负矩阵分解是一种非常有效的低秩逼近方法，它通过对非负矩阵进行非负因子分解得到数据的潜在特征。对于给定数据为X∈R M×N，非负矩阵分解的目的是把它分解为基因子U∈R M×K与低维表示因子V∈R K×N乘积的形式：

应用两种测度方式：Frobenius范数（简称F范数）和Kullback-Liebler（KL）散度来度量式（1）逼近程度，基于欧式距离的目标函数为：

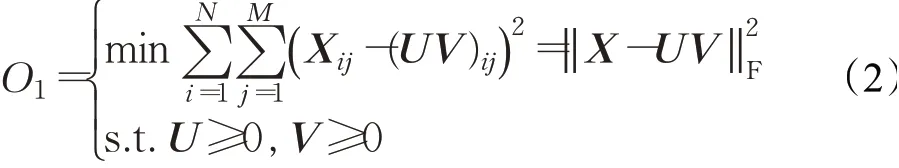
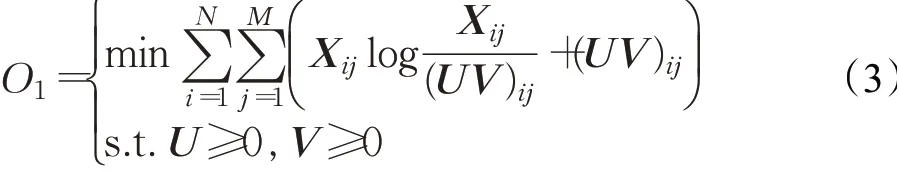
本文采用F范数求得分解后的非负基矩阵，针对目标函数（2），Lee和Seung给出了乘性迭代规则：

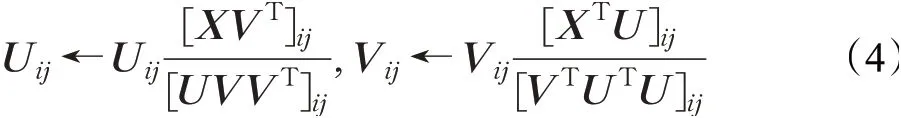
上述迭代算法（4）可以看成步长自学习的梯度下降算法。

1.2 基本分形编码

在基本分形编码中，首先将N×N原始图像分割成不重叠的Range块R i(i=1,2,…,Nr)和重叠的Domain块D j(j=1,2,…,Nd)，其中通常取X=2B，δ是滑动窗口的长度。

对于每个Domain块D j(j=1,2,…,N)，采用四领域像素平均，得到B×B像素块，用S（空域收缩算子）表示这种运算，即：

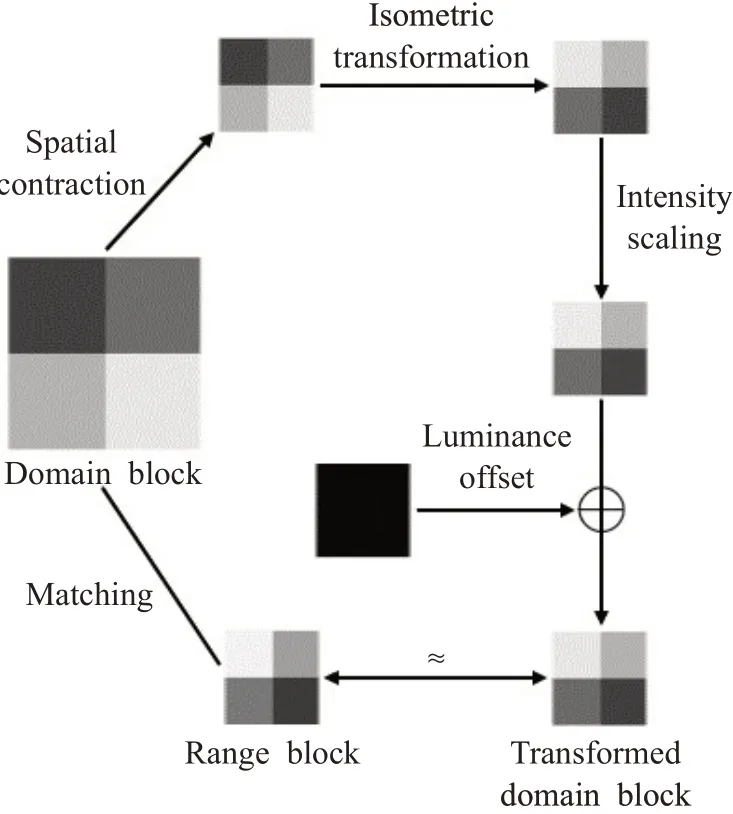
图1 范围块和域块之间的缩进仿射变换的过程Fig.1 Process of contractive affine transformation between range block and domain block

然后，在灰度匹配过程中对Domain块进行灰度变换。灰度变换是由亮度调整s和亮度偏移o两部分组成的线性变换。因此，可以得到Range块R与Domian块D之间的灰度变换：

这里，R、D分别是Range块和Domain块的灰度值，|s|＜1，s与o都为实数，I是灰度均为1的大小为B×B的常值块。根据最小误差函数E(R,D)计算Range块与Domain块之间的匹配误差：

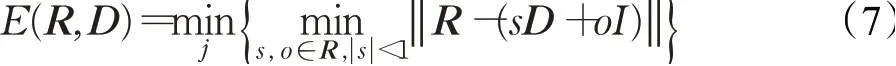
其中‖·‖是L2范数。通过最小二乘法可得参数s和o如下：

其中·,·为内积，和表示Range块和Domain块的

解码是一个相对简单的迭代过程，基于压缩变换的不动点定理和分形码进行图像重构。

1.3 稀疏分解

稀疏分解的目的是在海量的数据中选取一小部分重构新的数据[23]。在数学上，如果列向量B=[b1,b2,…,b K](b i∈R d)是有限维空间R中的一组基，则定义任意列向量X∈R d有：

其中S∈R K是向量X的系数和每个基向量上的投影系数。一般取B中的元素作为一组标准正交基，即任意两个基向量b i、b j满足：

如果基向量的个数等于空间维数，即K=d，那么这组基是完备的。稀疏分解的思想是利用少量的基向量来线性近似一个目标向量。因此，实现稀疏分解，需要基底完整，并且具有一定的冗余性。可以通过基底数量远远大于基向量的维数来实现，即K≫d。在稀疏分解中存在重构误差，一般用稀疏近似，其形式为：

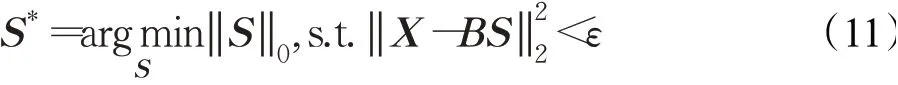
在保证重构精度的前提下，使系数向量达到稀疏最大化，有两种解决方案，分别是匹配追踪和正交匹配追踪。OMP[24]（orthogonal matching pursuit）是一种改进的MP[25]（matching pursuit），在OMP中残差与之前的线性部分保持完全正交，因此OMP具有更好的收敛性。

2 双层非负矩阵分解的分形图像压缩算法

2.1 投影非负矩阵分解

PNMF在原矩阵空间和特征空间上建立线性映射，不仅可以降低求解的复杂度，还可以得到更稀疏的解。对于一个秩为K的对称半正定矩阵P∈R M×M，存在非负矩阵U∈R M×K，使得P=UUT，将原始的非负矩阵X∈R M×N进行非负线性映射得到：

因此矩阵X可以表示为：

PNMF有两种测度方式，分别是Frobenius范数和Kullback-Liebler（KL）散度。下面仅介绍基于欧式距离的目标函数：

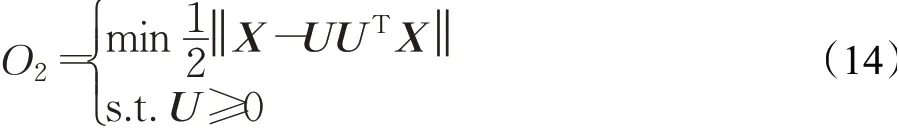
根据目标函数式（14），更新规则如下：

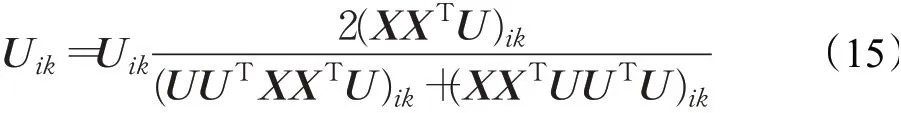
相比NMF方法，PNMF方法将系数矩阵V∈R K×N替换为UTX，引入投影限制，并且在非负分解的过程中要求投影矩阵P接近单位矩阵。说明PNMF方法隐含了基矩阵的正交性，这样可以获得更稀疏的特征矩阵。

2.2 提出的非负矩阵分解

NMF将原始数据矩阵分解为两个非负矩阵U和V的乘积，分解后的矩阵仅包含非负因子，并且基向量U可以很好地保持数据的局部结构。但是NMF得到的解不够稀疏，收敛速度慢。PNMF可以将原始矩阵投影到特征空间，能很好地表示数据隐藏的属性，对于正交限制的隐藏可以获得更稀疏的矩阵。

对于范数稀疏约束方法而言，主要有：L0范数、L1/2范数、L1范数、L3/2范数、L2范数。

Lq是一组范数，根据q的变化，范数有着不同的性质。L0范数是NP难问题，而L1是L0的最优凸近似，相对L0范数要容易优化求解。L2范数可以实现正则化约束中的每一个元素都接近于零，而L1范数趋于产生稀疏的特征，其他元素都是零。通过L2范数实现正则化的同时在一定程度上避免了过拟合，从而提升泛化能力，还可以使得优化求解变得稳定和快速，一般用于目标函数求损失函数。

近年来，分数范数Lq(0＜q＜1)被很多学者提出，当分数q取不同值时，得到比L1范数更稀疏的解。在文献[26]中，Krishnan等证明L1/2范数和L2/3范数正则化约束是非常高效的约束。在文献[19]中，Du等表明Lq和L1/q具有相同属性，当q＞1时，L3/2范数的正则化项是一个凸的光滑范数，验证了L3/2范数约束在稀疏表示上具有很好的约束效果。

因此本文将PNMF与L3/2范数的稀疏约束相结合，提高矩阵分解的鲁棒性和稀疏性，目标函数如下：

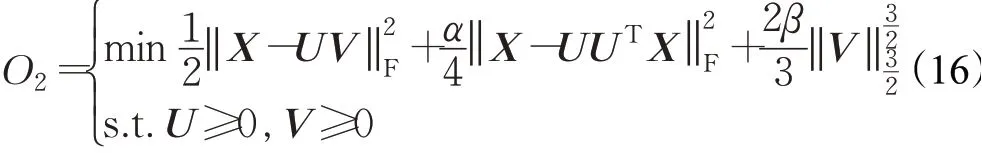
其中∂、β是正则化参数（在仿真实验中α、β均取10-3），目标函数可写成如下形式：

下面对拉格朗日函数关于U、V求偏导：

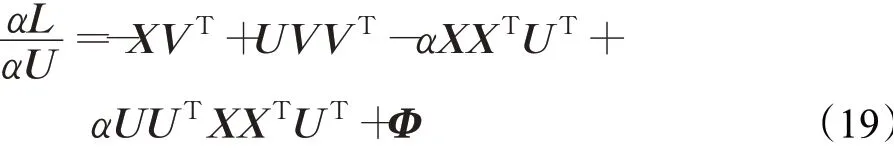
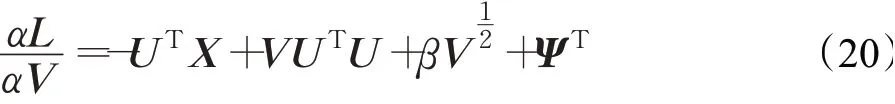
根据KKT条件φik U ik=0，φkj V kj=0，使得：

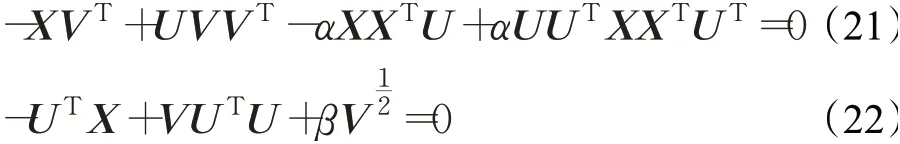
进一步化简，可以得到关于U、V的更新迭代公式：

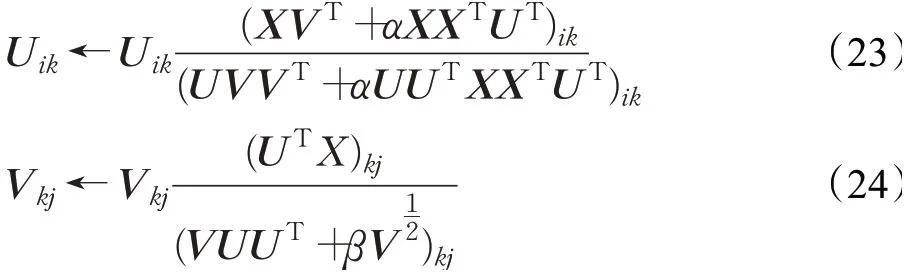
使用梯度下降的方法对U、V进行如下更新：

其中ηik、ςkj为步长参数，计算可得：

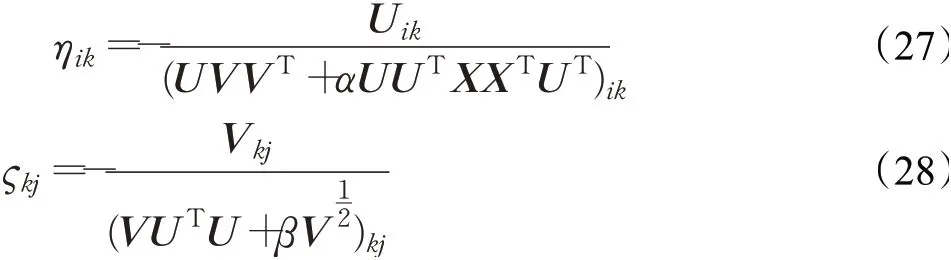
为了证明目标函数O2的收敛性，需要证明式（23）和（24）在更新过程中是不增的。由于U的证明过程和V的证明过程类似，这里只对V进行证明。将遵循类似于文献[27]的描述过程。证明过程需要用到辅助函数，类似于期望最大化算法[28]中使用的函数。

定义1G(v,v′)是F(v)的辅助函数，如果G(v,v′)≥F(v)，则有G(v,v)=F(v)。

根据如下引理，辅助函数将非常有用。

引理1如果G是F的辅助函数，F在如下迭代中是不增的：

证明

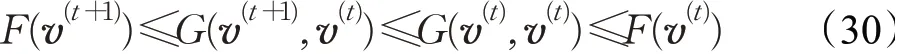
现在，将证明式（24）中v的更新满足式（29）中带有辅助函数的更新。目标函数O2可表示为：

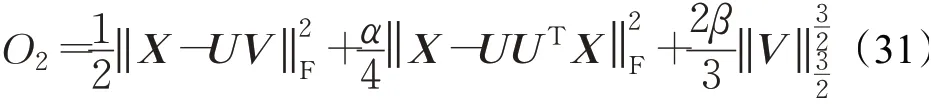
这里用Fab表示O2中只与v ab相关的部分，对于V中任意元素v ab，有：

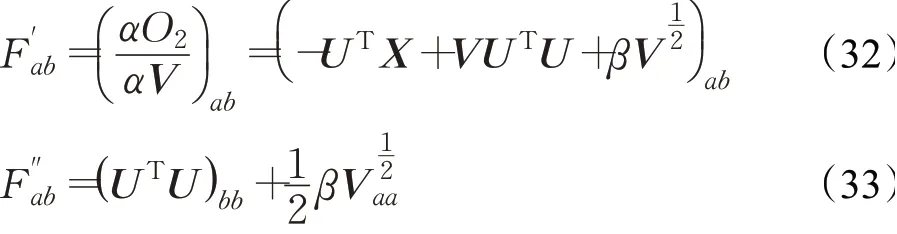
由于V的更新本质上是元素的更新，这足以表明每一个F ab在更新步骤（24）下是不增的。

引理2函数：

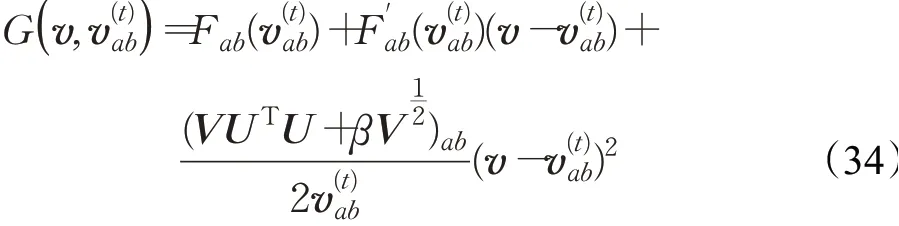
是O2的部分辅助函数，只与V ab相关。

证明由于G(v,v)=Fab(v)是显而易见，这里仅需要验证为此比较Fab(v)的泰勒级数展开：

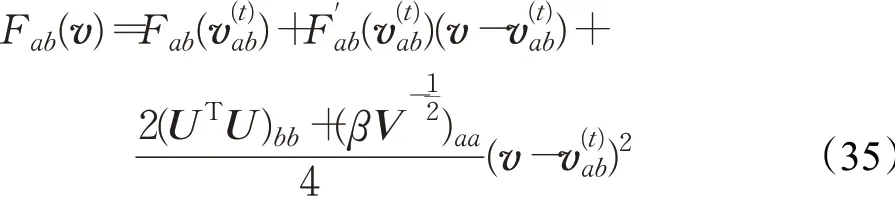
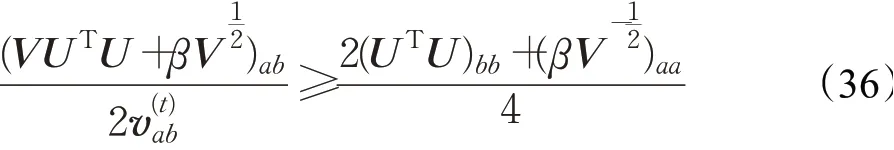
由于

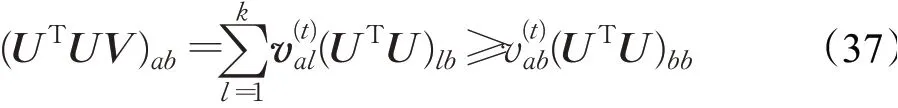
并且

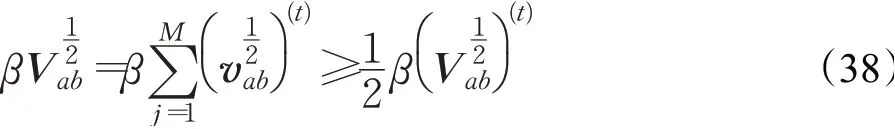
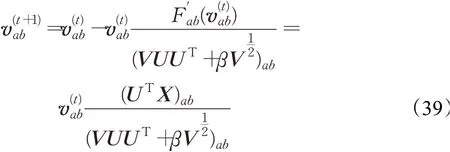
2.3 正交稀疏分形编码过程

稀疏分解的编码过程可以看成线性分解求系数矩阵的过程，因此，需要找到每个Range块在虚拟码本中的若干个基向量的最优线性组合。根据稀疏分解，一个新的灰度变换定义[29]如下：

通过进一步研究E(R,D)，可以发现：

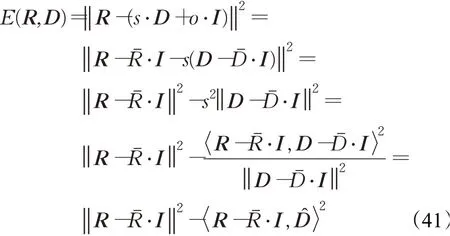
根据以上推算过程可以得到R-Rˉ·I和D^能够用来计算匹配误差E(R,D)。通过直接计算R-Rˉ·I,D^2的最大值作为Domain块的最优匹配块。基于此方法，基本分形编码中的灰度变换公式（6）可以定义为如下形式：

其中sj(j=1,2,…,k(k≤K))是尺度参数。正交稀疏分形编码方法直接计算尺度参数s，减少了计算的复杂度和迭代次数。

2.4 算法分析

根据上述计算，可以得到基于PNMF方法与L3/2稀疏约束结合的更新迭代过程。在进行分形图像压缩时，为了尽可能得到更稀疏的图像特征，本文对图像的灰度值矩阵进行了双层非负矩阵分解，使分解结果尽可能的稀疏，获得原始图像的特征向量。结合DLNMF、Kmeans和OMP稀疏分解的思想，提出了一种双层非负矩阵分解的分形图像压缩编码算法。

本文采用二分K-means聚类[30]，可以有效地避免K-means聚类中在第一步中随机选取初值中心敏感带来的影响，保证了每一步误差最小并且能够克服Kmeans收敛于局部最优。利用二分K-means聚类将虚拟码本Ω进行分类，根据稀疏分解的思想在相应的类别块里进行正交稀疏分形编码，不仅可以提高Range块与Domain块的匹配搜索效率，而且可以提高匹配重建图像的质量。

2.5 算法实现

基于以上算法分析，下面给出所提出算法的具体过程。

算法1双层非负矩阵分解的分形图像压缩算法

输入：原始图像I。

（1）图像分割。把原图分割成互不重叠的大小为n×n的固定Range块，记为R块。

（2）码本构成。对同一幅图像，在纵横方向上按滑窗步长均为δ（一般的，取δ=2n）个像素来生成尺寸为2n×2n的Domain块，记为D块。对于每个D块，采用4-邻域像素值平均得到n×n的图像块，并考虑8种等距变换，这样的子块集合构成码本Ω。

（3）计算图像特征向量。对原始图像的灰度值矩阵进行DLNMF。

①根据非负双重奇异值分解初始化[31]得到初始矩阵U0和V0。

②首先，进行第一层的非负矩阵分解，根据目标函数：

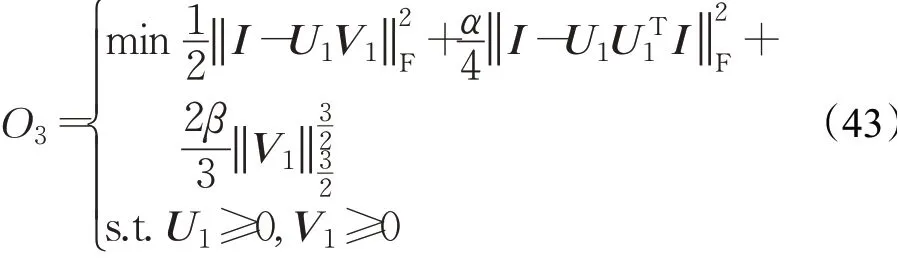
得到基矩阵U1。然后进行第二层的非负矩阵分解，由目标函数：

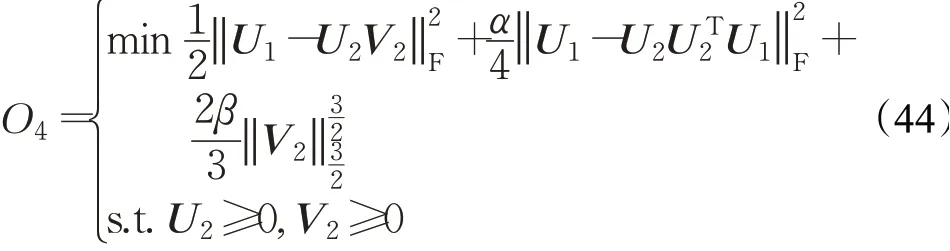
得到基矩阵U2。

③对双层非负矩阵分解的基矩阵U2进行归一化，得到图像的特征向量U3。

（4）根据原始图像的特征向量U3进行K-means聚类。利用特征聚类索引将图像的虚拟码本Ω划分成C类。

（5）用OMP算法进行稀疏灰度匹配处理。

对于每一个R块R i，设置初始残差e0=R i-Rˉi·I，索引集Λ0=∅，初始化D块B0=∅，迭代次数t从1到K。

①找出残差e t-1与相应类别字典D中某一列D^j的内积最大值对应的下标λ，即：

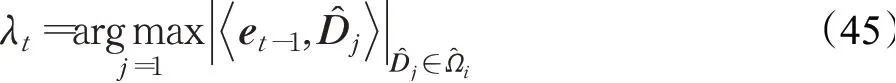
②更新索引集Λt=Λt-1⋃{}λt，更新所选字典子列构成的集合B t=[B t-1,D^λt]。

③利用最小二乘法得到K阶逼近：

④更新残差e t=e0-B t s^t。如果‖ ‖e t2＜emin，则迭代停止；否则，继续步骤①。

（6）解码。根据分形码重建图像。

3 实验结果和分析

为了测试文中提出方法的效果，选择标准测试图像Woman2、Aerial、Barbara、Boat、Goldhill、Zelda、Milkdrop、Plane和Lake（512×512，8 bit量化）为实验对象，在仿真实验中，实验平台为运行Windows10家庭版的Intel®CoreTM（2.60 GHz CPU/16.0 GB内存），程序用MATLAB编写。测试性能的参数为编码时间T（单位：s）和峰值信噪比PSNR（单位：dB）。实验中采用一致方块分割，并选取R块大小为8×8，生成D块池滑窗步长是8。

3.1 评价标准

一般采用峰值信噪比PSNR来评价原始图像和重建图像间的相似度：

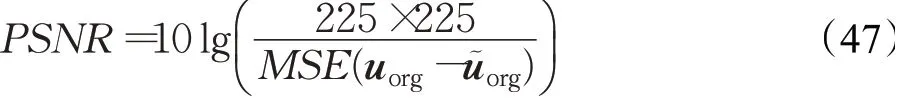
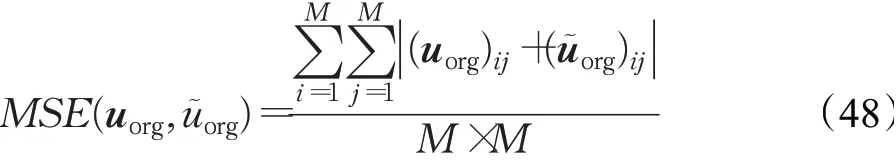
3.2 参数的选择

在改进的方法中，OMP算法下的稀疏度K、OMP算法下的重构误差阈值emin和K-means聚类过程中的聚类数C，这三个参数在编码的过程中影响重建图像的质量（PSNR）和编码时间（Time）。因此，需要进一步确定算法中的三个参数得到最佳的实验结果。

参数K是正交稀疏匹配过程中灰度值的稀疏程度，K值越大表示匹配获得的灰度值越多，重建图像的质量越好，但是由于数据变多，编码过程中耗费的时长也会增加。根据图2综合峰值信噪比和编码时间可以看出，当K=10时，获得的编码结果相对更好。

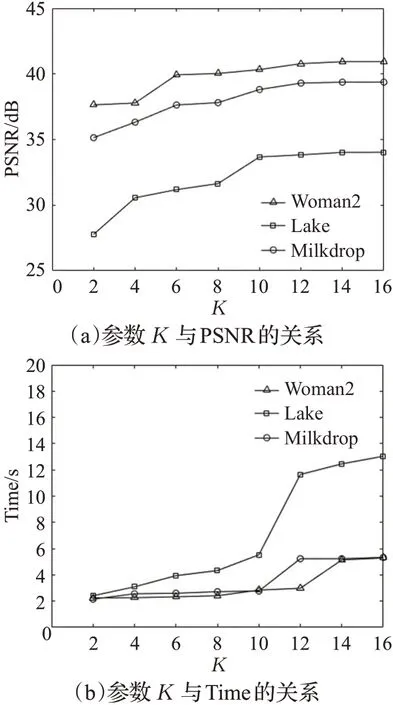
图2 参数K对分形图像压缩编码的影响Fig.2 Influence of parameter K on fractal image compression coding

参数emin是正交匹配搜索的终止条件，其目的是进一步区分出Range块的纹理特征。对于纹理复杂的Range块需要通过增加虚拟码本的数量来提高重构质量。emin的值越大表示正交匹配的误差阈限要求越低，导致重建的图像质量降低，编码时间减少。观察图3可以发现，当emin∈( )20,30时，PSNR和Time的变化比较快，本文中emin取25。

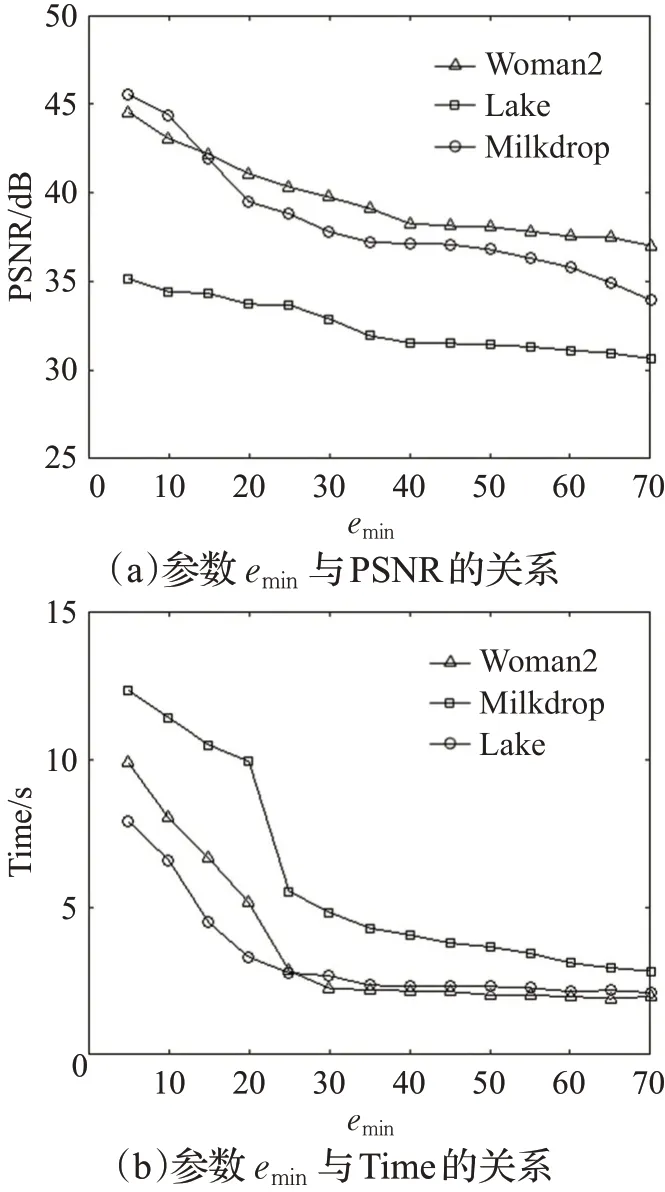
图3 参数e min对分形图像压缩编码的影响Fig.3 Influence of parameter e min on fractal image compression coding

参数C是K-means算法的聚类数，编码时相应的图像块划分的类别数越多，编码的复杂度会增加，从而影响PSNR和Time。通过图4观察参数C取不同值时，图像的重建质量有所下降，编码时间也随之增加，综合PSNR和Time两个因素，C=10时，重建图像效果较好。

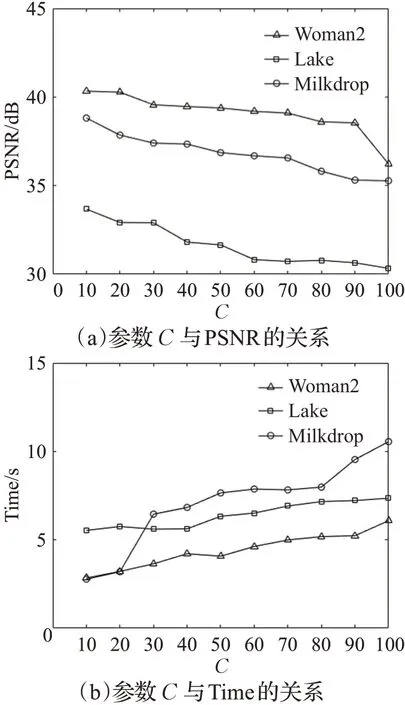
图4 参数C对分形图像压缩编码的影响Fig.4 Influence of parameter C on fractal image compression coding

3.3 结果和分析

使用Woman2、Aerial、Barbara、Boat、Goldhill、Zelda、Milkdrop、Plane和Lake图像将本文算法分别与基本分形算法[32]、快速稀疏分形算法[33]和小波分形算法[8]进行比较，稀疏度K=10，重建误差阈限emin=25，类别数C=10，实验结果见表1～表3，表中用加粗字体标出了本文算法在重建图像时峰值信噪比提高的值和编码时间减少的值。

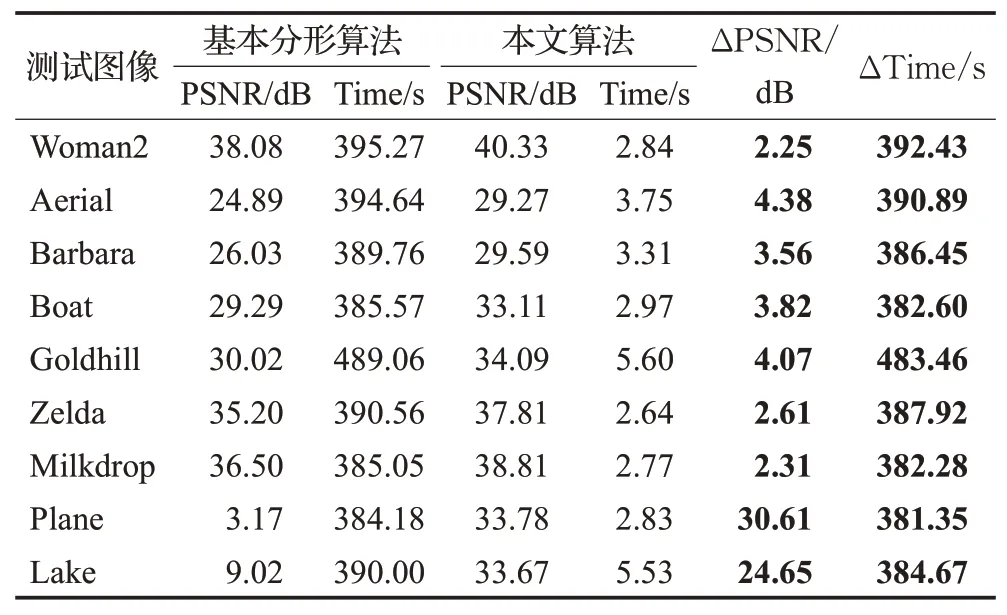
表1 基本分形算法和本文算法算法实验对比Table 1 Experimental comparison between basic fractal algorithm and algorithm of this paper

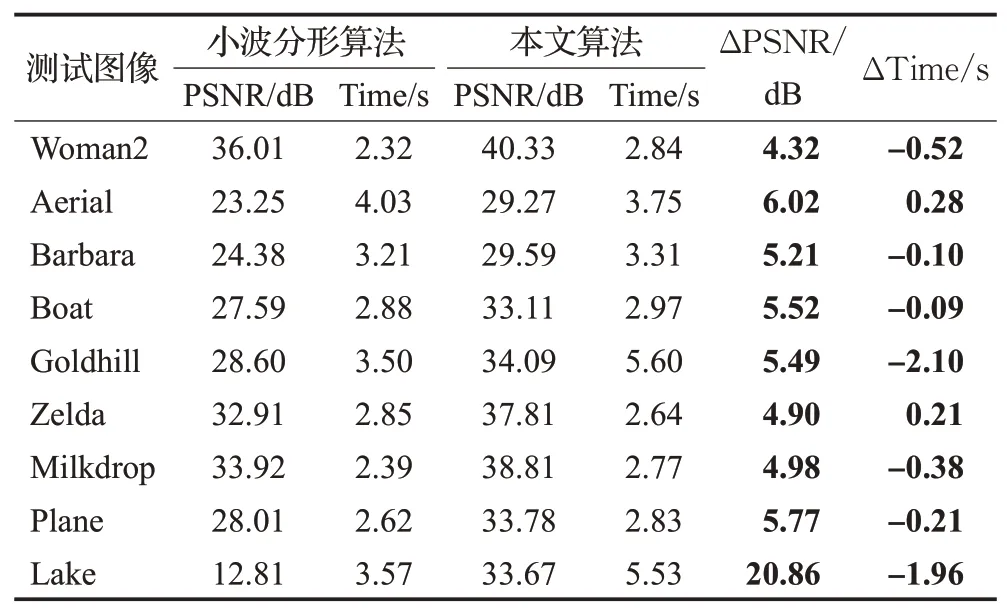
表3 小波分形算法和本文算法实验对比Table 3 Experimental comparison between wavelet fractal algorithm and algorithm of this paper

基本分形算法采用全搜索方法求解，虽然可以得到质量较好的重建图像，但是耗费大量的时间。提出的方法在快速稀疏分形编码的基础上，利用NMF高效的无监督提取灰度值特征的性质，提出了DLNMF有效缩减码本信息，并且根据提取的灰度特征将图像块进行了分类处理，提高编码效率。从表1中可以看出改进方法在重建图像质量上和编码时间上都有很大的提高，其中最为明显的是在基本分形算法中，Plan和Lake的重建图像的峰值信噪比非常低，改进方法提高了30.61 dB和24.65 dB。

快速稀疏分形算法采用了正交匹配追踪的思想，提高了Range块与Domain块的匹配效率，但是实验结果表明该方法有待进一步完善。本文算法在快速稀疏算法的基础上加入特征提取及分类匹配的方法进行优化，由表2可以发现，重建图像质量和编码时间都有所提高。

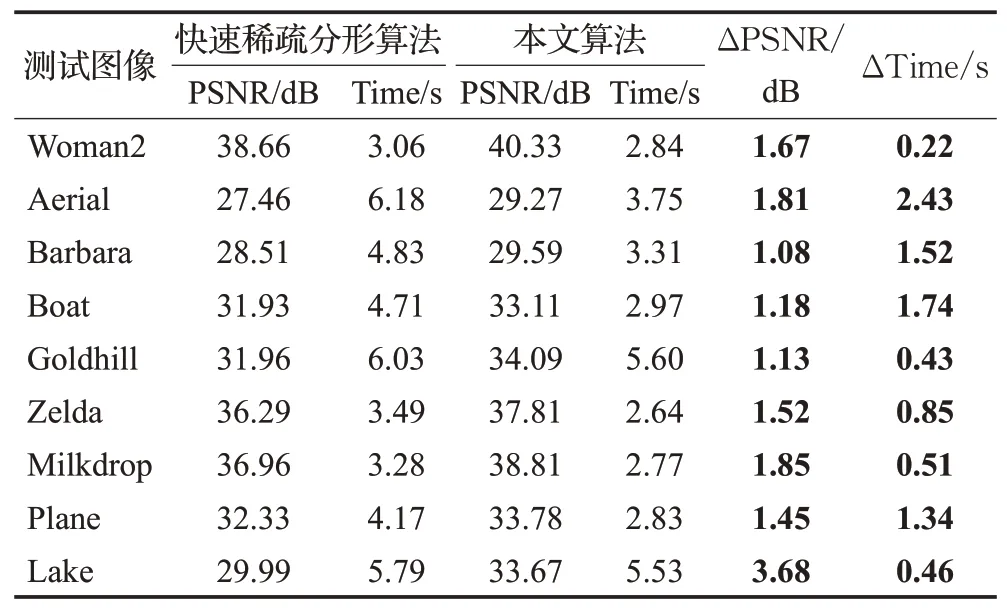
表2 快速稀疏分形算法和本文算法实验对比Table 2 Experimental comparison between fast sparse fractal algorithm and algorithm of this paper

小波分析自创立以来，在分形理论上的应用就日渐广泛。小波分形编码算法利用小波变换后多级子带之间具有相似性，将全局匹配变为邻域匹配，提高编码速度，但是重建图像的质量并不理想。观察表3可以看出，在小波分形算法和改进算法的比较中，可以发现本文算法在重建图像质量上都有非常大的提升，尤其是Lake的峰值信噪比，提高了20.86 dB，是改进算法的近2.63倍，但是在编码时间上部分略快一些。

将四种算法的峰值信噪比PSNR展示在图5上。在图6中只展示其余三种算法。

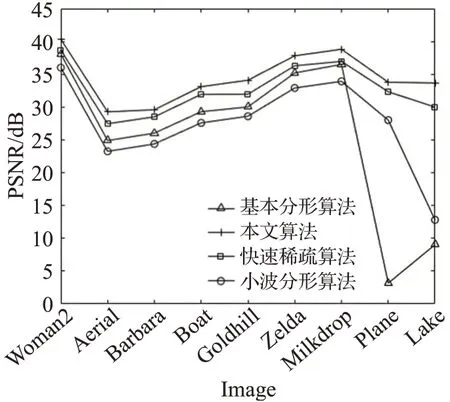
图5 四种算法在9幅图像压缩的PSNR对比结果Fig.5 PSNR comparison results of four algorithms in 9 images compression

观察图5和图6可以看出，改进算法在重建图像质量和编码效率上都有改善。

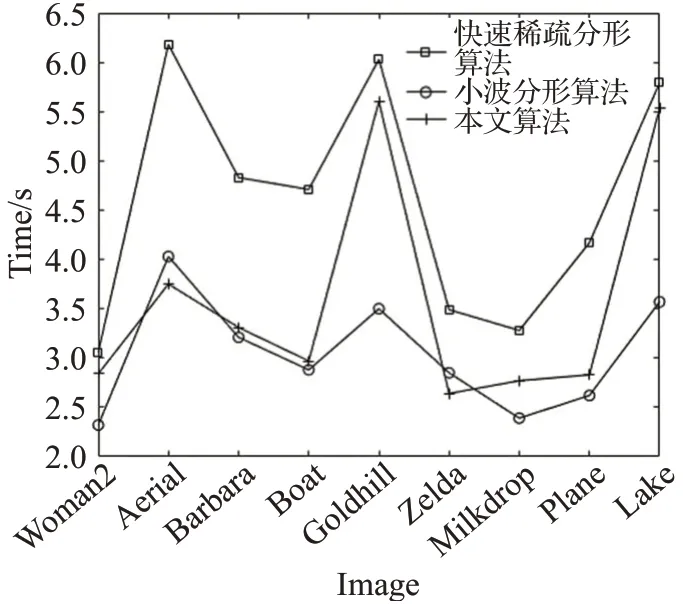
图6 三种算法在9幅图像压缩的Time对比结果Fig.6 Time comparison results of three algorithms in 9 images compression

这里选取了纹理复杂度不同的四幅图像，分别是Milkdrop、Woman2、Lake、Goldhill。将四幅图像在四种算法（基本分形算法[32]、快速稀疏分形算法[33]、小波分形算法[8]、本文算法）下进行仿真实验，得到图7，截取其中一个片段放大处理。

图7 四种算法的重建图像Fig.7 Reconstructed images of four algorithms

目前图像压缩从大体上看已经有相对良好的水平，但是部分细节还需要进一步完善和优化。从仿真实验得到的图像中可以看出，纹理相对简单的图像对比效果更明显。根据四种算法得到的图像1、图像2、图像3和图像4，分别将它们与原始图像进行对比，观察图8可以看见图像4与原图最接近，有的地方甚至比原图更清晰。在图像4中实物的边缘部分更光滑，而图像3与原图比较最模糊，在放大的图像3中只能看见大致的实物结构。图像2仅次于图像4，比图像1清晰。通过仿真图像的对比可以发现本文的算法得到的图像效果更好。

图8 四种算法的重建图像的部分放大图Fig.8 Partial enlarged view of reconstructed image of four algorithms

本文根据原始图像的特征分类索引，将字典分成了相应的类别块，在相应类别块中利用正交稀疏方法，记录其与初始化残差乘积最大值对应的位置，通过迭代得到满足重构误差限下的最佳匹配Domain块的序号，根据序号找到分形图像的Range块。快速稀疏分形编码算法每次迭代都需要将整个字典与残差做内积，因此用改进方法计算内积在很大程度上减少编码时间，并且在相应类别块中搜索，可以缩小搜索范围、提高匹配的准确率。图像Woman2、Lake、Milkdrop的匹配效率分别是91.18%、93.52%、90.43%。根据数据可以发现改进算法的匹配效率均超过了90%，改进算法利用稀疏思想减少信息冗余，在保证高匹配效率的同时，解决了基本分形算法耗时的问题。

4 结束语

针对分形图像在压缩后，重建图像的质量和时间不理想，本文算法利用NMF无监督特征提取的性质，将PNMF与L3/2范数约束相结合，利用稀疏分解来改进分形压缩算法，提出了双层非负矩阵分解的分形图像压缩算法，提取的图像特征具有稀疏性和鲁棒性。在仿真实验中，对比四种算法可以发现本文算法在分形图像编码时，显著改善重建图像的细节效果。今后可以尝试将本文算法运用在对于重建图像质量要求较高的分形图像压缩领域，如医疗图像或者存档扫描的图像等有价值图像的保存和传输。除了运用本文算法进行特征提取外，还可以尝试其他方法提高分形图像重构的匹配搜索效率，进一步缩短编码时间。