总结性自适应变异的粒子群算法

陈博文，邹 海

安徽大学 计算机科学与技术学院，合肥 230601

粒子群优化算法（particle swarm optimization，PSO）作为进化计算的一个分支，是由Eberhart和Kennedy等[1]于1995年提出的一种全局搜索算法，通过模拟动物在群体活动中所表现出来的信息共享特性完成对目标问题的求解。相关的群智能算法应用广泛，如文献[2]中通过改进蚁群算法解决旅行商问题，文献[3]中使用果蝇优化算法解决图像分割问题。PSO最早是用来优化神经网络的网络连接权重的，现已涉及多目标优化[4]、信号控制[5]、资源调度[6]等各个领域。

需要合理地对PSO的参数进行配置，平衡算法在迭代过程中对全局和局部的搜索能力，来优化整个收敛过程。Shi和Eberhart[7-8]分析了惯性权重对粒子搜索能力的影响，在粒子的寻优过程中，惯性权重随着迭代次数来线性递减，在保证广度和精度的基础上提高了算法的收敛性。Ao等[9]提出的自适应惯性权重的改进粒子群算法，将适应度值较差的粒子的惯性权重因子置零，充分发挥全局最优的指向性，提高了算法的收敛性。郭巳秋等[10]通过控制粒子群的数量来验证惯性权重对整个算法收敛的影响。周蓉等[11]提出的基于灰狼优化的反向学习粒子群算法中，引入余弦函数和贝塔分布来控制惯性权重的非线性变化，再次提高了算法的搜索效率。

目前，不同的改进策略对粒子群算法在求解问题时均有不同程度的提高，但仍然存在精度不高、收敛速度慢等缺陷。针对这些问题，本文新提出一种总结性自适应变异的粒子群算法，与相关变种算法对比，证明了该策略的稳定性、有效性。

1 基本粒子群算法

在PSO算法的模型中，每个粒子都代表着搜索空间的潜在解，并有可能成为群体的最优解，他们都以一个共同的全局最优作为自己的“标杆”。每个个体粒子在进化的过程中维护两个向量，分别为速度向量V i，位置向量X i，其中i表示粒子的编号，D是求解问题的维数。粒子的速度向量控制着其运动的方向和速率，而位置则体现了粒子所代表的解在解空间中的位置，正是通过计算适应度的值来判定该解的质量。

开始寻优过程，对每个粒子i各维的速度和位置进行更新，其公式如下：

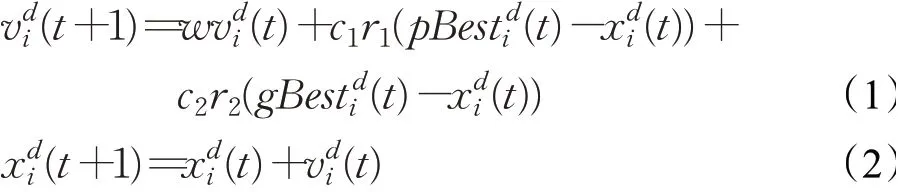
其中，d代表当前维度，t表示当前的迭代次数，r1和r2表示[0，1]之间的随机数，c1和c2代表学习因子，w作为速度的系数，控制了前一次迭代的速度对当前速度的影响，即惯性权重，pBest为各个粒子自身维护的历史最优位置向量，来确保粒子不会逆向寻找最优，gBest为整个群体维护的全局最优向量。因此粒子群算法在考虑了个体的自我认知和社会信息共享的基础上也保证了粒子的随机性。

2 SCVPSO算法

2.1 新的惯性权重自适应函数

在PSO算法中，惯性权重代表了前一次迭代各个维度的速度对当前速度的影响，因此惯性权重w的取值在整个收敛过程中会直接作用于各个粒子的寻优能力。本文截取logistic回归曲线[-6,6]之间的图像通过数学变换处理，提出新的非线性惯性权重衰减策略，其关于迭代次数的关系如式（3）所示：

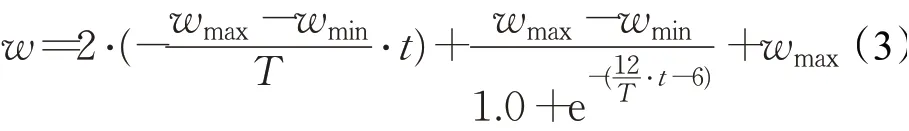
其中，T为最大迭代次数，t表示当前的迭代次数。wmax、wmin分别为最大惯性权重和最小惯性权重。本文wmax=0.8,wmin=0,T=1 000，绘制其变化曲线如图1所示。相关研究表明，w小于0.8时，能以更快的速度达到全局最优值[7]。在此基础下，本文再将惯性权重变化分为下降、上升、再下降三个部分。这满足在迭代初期，惯性权重取最大值并逐渐下降，便于提升粒子的全局搜索能力[12]，且下降呈凹函数趋势，保证了寻优时的收敛效率[13]；在迭代中期，惯性权重转折上升，即各个粒子前一次迭代速度的影响增大，则扩大了问题搜索空间，方便算法发挥其寻优性能；在迭代后期，随着迭代次数增加，惯性权重逐渐减小到最小值，最大化粒子的局部开发能力[14]。从整体来看该策略呈现递减趋势，平衡了在迭代时全局与局部的搜索能力，这符合文献[15]指出的应以较大的w值进行全局搜索，以较小的w值进行局部搜索。

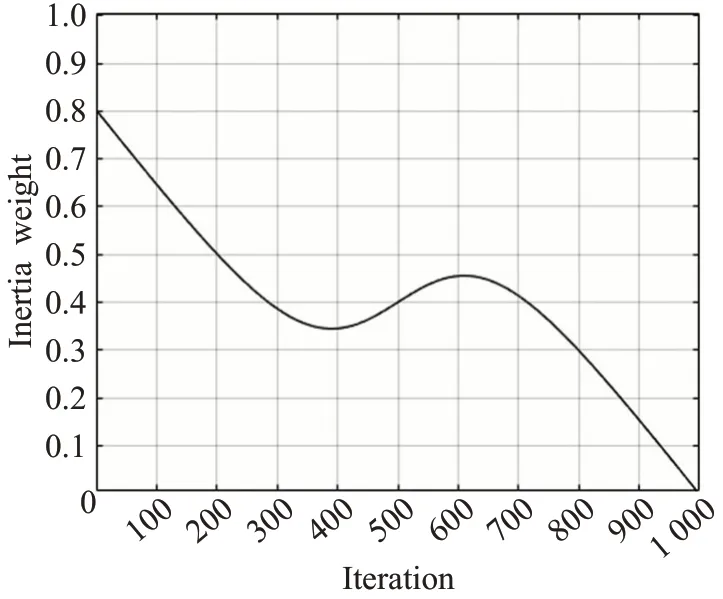
图1 SCVPSO算法惯性权重曲线Fig.1 Inertia weight curve of SCVPSO

2.2 局部粒子反向搜索处理

每个粒子在寻优过程中，虽然有着全局最优粒子的引导，但由于随机参数r1和r2的存在，难免会出现部分粒子pbest值停滞的现象，对于这种超过规定次数后仍无pbest值更新的粒子，将其认定为局部粒子。由于寻优资源的有限性，局部粒子会影响种群的搜索效率。

为改善该情况，这里自定义了一种干预策略。如图2为示例四种情况下，局部粒子在最近3次迭代过程①②③中位置发生了变化，若pbest值无提升即出现停滞现象，说明该粒子所在局部区域未搜索到更优解，且粒子速度过于发散会导致后期收敛速度慢[16]，此时在第4次干预其寻优的方向以及大小，该速度聚合了前三次速度矢量和，帮助局部粒子更快进入有效区域，在限定迭代次数中能够提高种群的寻优能力。拟将被干预的粒子位置更新公式如下：

图2 SCVPSO算法反向搜索示意图Fig.2 Reverse search of SCVPSO

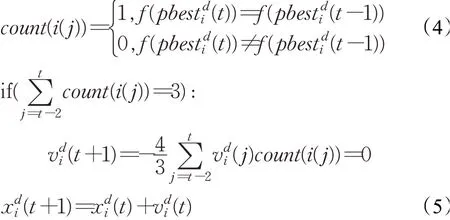
其中，i(t)表示第t次迭代中的粒子，count(i(t))表示第t次迭代时的粒子个体最优值是否与前一次迭代时个体最优值相等，1表示相等，0表示不等，以此来记录是否连续三次粒子处于被动的局部状态；表示连续三次的个体最优值未发生变化的次数。若，则该粒子被判定为局部粒子，并对个体当前速度更新策略进行调整；取-4/3作为系数，使当前速度与前三次速度矢量和相反。由于在前三次速度更新已经融合了随机性，为提高计算效率这里无需添加随机因子，个体位置更新后，将其count值重新设定为0。

2.3 劣势粒子位置总结性变异

拟对各个粒子进行自我总结性观察，引入新的参数scr（self-conclusion rate）自我总结率，该参数为近期各个粒子的寻优情况与全局最优粒子的变化比率，根据scr的值以对算法寻优进程进行分析，对筛选出的劣势粒子作出相关处理，从而跳出当前的劣势区域，有效防止其陷入局部最优。其中scr表达式如式（6）所示：

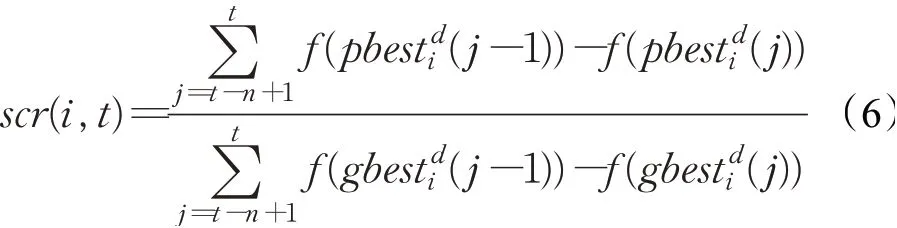
其中，scr(i,t)表示在第t次迭代中，第i个粒子在前n次迭代中的个体最优适应度值提升总量和全局最优粒子提升总量的比值。本文中n取5，因此式（6）中分子代表了个体粒子的近5次迭代提升，分母则代表了近5次全局粒子的提升效果。

在以下三种情况下，该粒子均判定为劣势粒子：scr(i,t)为无穷大Inf时，表示全局最优粒子gbest近期寻优停滞不前；scr(i,t)为0时，表示个体最优粒子pbest近期无寻优提升；scr(i,t)为异常空值NaN时，表示整个种群陷入了局部最优值。在粒子出现上述三种情况时，本文认定该粒子符合变异条件。受遗传算法[17]的思想启发，将劣势粒子和全局最优粒子进行位置单向变异，其基本步骤如图3所示。

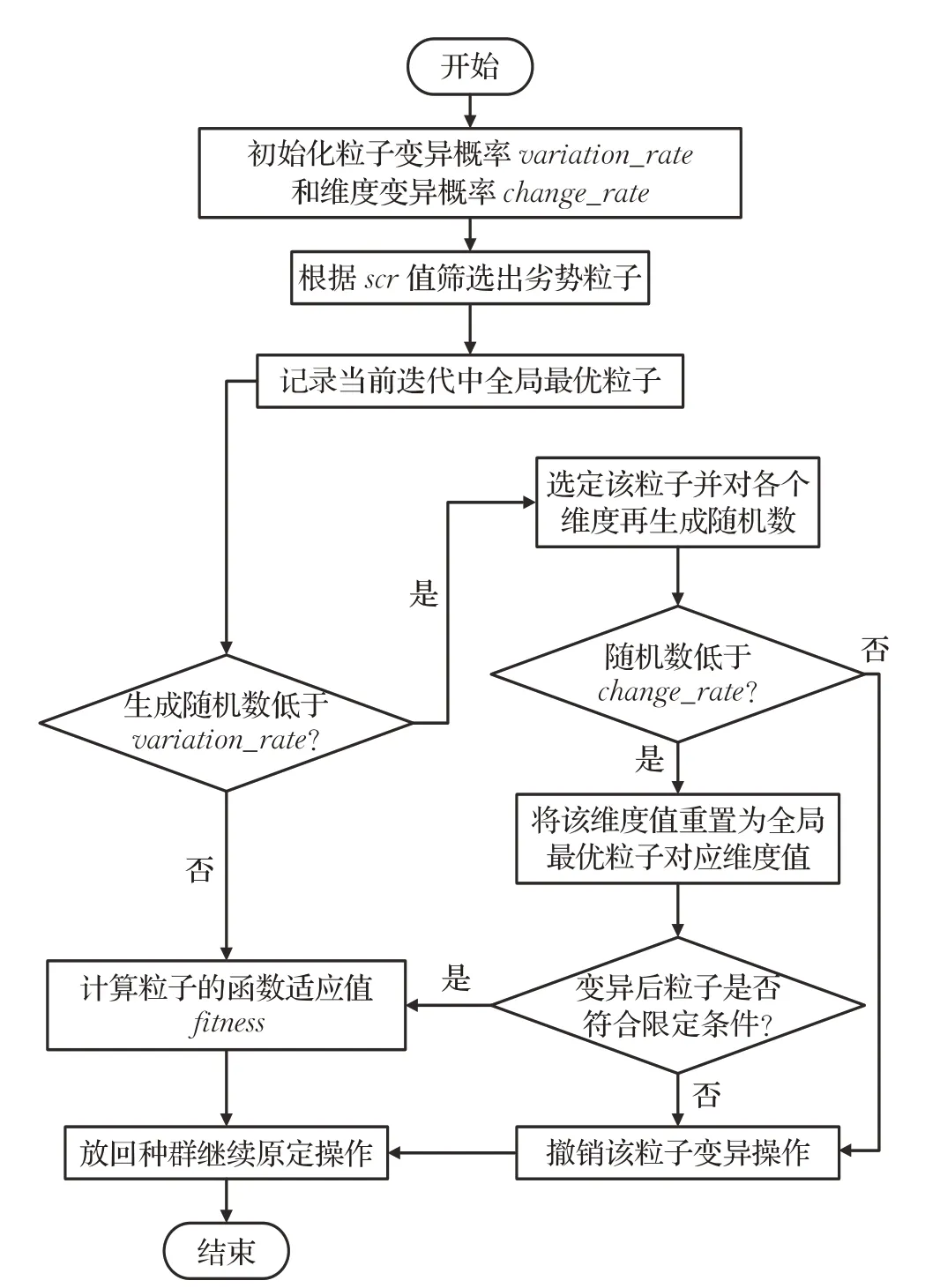
图3 SCVPSO算法变异部分Fig.3 Variation part of SCVPSO

变异具体流程如下：

（1）初始化，设置粒子变异概率variation_rate，决定该粒子向最优粒子跃迁的几率，设置维度变异概率change_rate，决定该维度是否需要变异为最优粒子对应维度值。

（2）总结变异条件，在第t次变异，取t-n至t-1次实验为例，计算粒子的scr值，筛选出符合条件的劣势粒子。

（3）记录最优，采用异步刷新的方式来记录最优粒子的位置gbest_position。

（4）单向变异，根据variation_rate选择出执行变异的粒子，采用轮盘赌选择算法思想，将生成[0，1]之间的随机数与change_rate再比较，二次筛选出劣势粒子的维度值并与当前最优粒子gbest_position进行交换，单向重置劣势粒子位置。

（5）确认正确，检查此次变异后的粒子是否符合既定条件，重新计算适应度值并放回种群。

如表1所示，为说明单向变异对粒子状态的改进程度，选取了表2中的测试函数F3,D=30时部分粒子在迭代过程中scr参数值的变化，各个粒子在迭代中筛选判定为劣势粒子后（粗体标出），通过概率单向变异策略及时在后续迭代中做出调整，使scr值回归正常，说明粒子跳出当前区域改善了劣势状态。与文献[18]通过引力系数让粒子进行社会学习相比，本文中单向变异学习了最优粒子的位置优势，且引入概率保证了粒子本身活性，在增加种群多样性的基础上提高了粒子寻优效率。

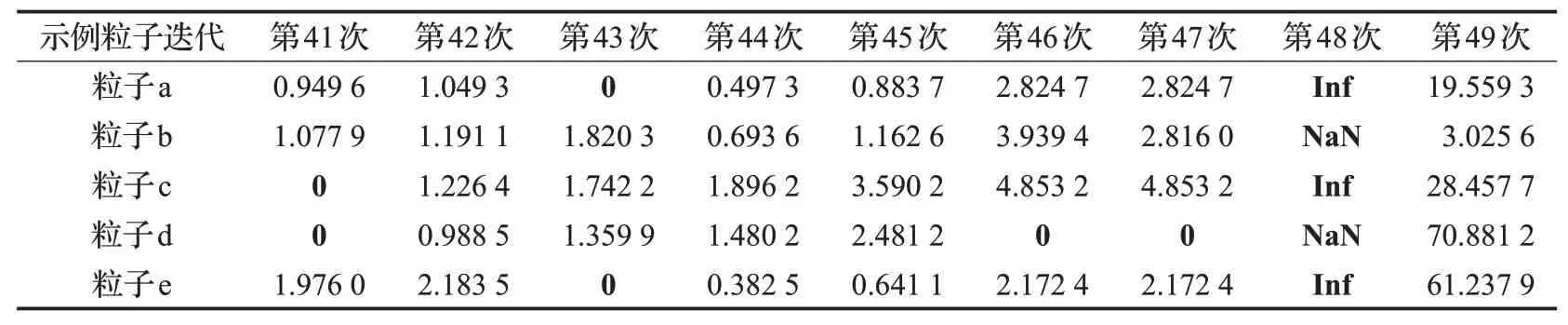
表1 迭代时部分粒子scr参数值变化表Table 1 Change of scr parameter value of some particles during iteration

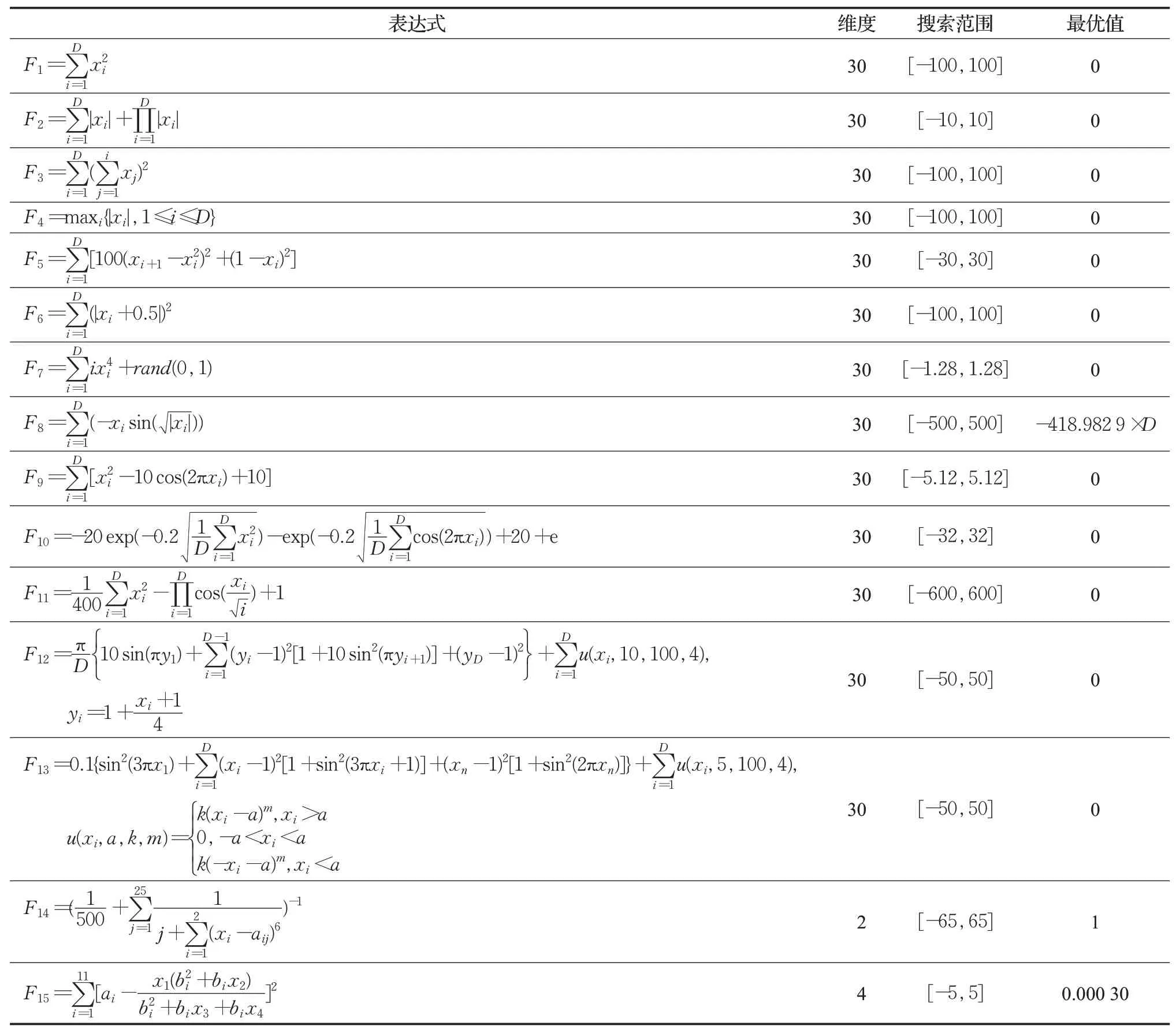
表2 基准测试函数Table 2 Benchmark function

2.4 算法流程

综合2.1～2.3节的相关改进分析，本文提出的总结性自适应变异粒子群算法具体步骤如下：

步骤1初始化所有的粒子，包括速度和位置，设置相关的参数T,wmax,wmin,c1,c2,variation_rate,change_rate等。

步骤2计算每个粒子的适应度值，初始化个体最优位置pbest和全局最优粒子适应度值gbest，为后续的迭代做准备。

步骤3迭代的同时来计算近n次的变化量，累计不变次数超过规定次数时对筛选的局部粒子做反向处理。

步骤4实现队列来循环缓存近期的pbest和gbest值，并在每个粒子位置更新结束后计算出其自我总结率scr值，按既定条件筛选出劣势粒子并实现2.3节中的单向变异。

步骤5与自身的历史最优值pbest进行比较，较优的值作为个体的最优值，同时判断并异步更新全局最优粒子值gbest。

步骤6在未达到结束条件时，转到步骤2继续向下执行，直到结束，找到规定迭代次数中的gbest值以及其对应的位置。

按照给定的参数设置以及限定条件来执行整个流程。

3 实验及结果分析

3.1 实验测试函数

为了检验改进后算法性能，选取了如表2中所示的15个基准测试函数进行测试，已确定各个函数搜索范围和最优值，其中F1～F7为单峰测试函数，F8～F13为多峰测试函数，F14、F15为固定维度多峰测试函数。

3.2 惯性系数提升对比

为了直观展示不同w对算法的影响，验证本文方案的可行性，将其与一些其他的w惯性权重方案做比较。其中有文献[8]中原始的线性递减函数w1，文献[19]中关于迭代次数差的1.2次幂下降方案w2，文献[20]中关于0.98的幂函数w3，文献[21]中使用的关于迭代次数的余弦函数w4，文献[12]中使用的正态分布衰减策略的改进方案w5，本文提出的方案为w6，如图4所示。

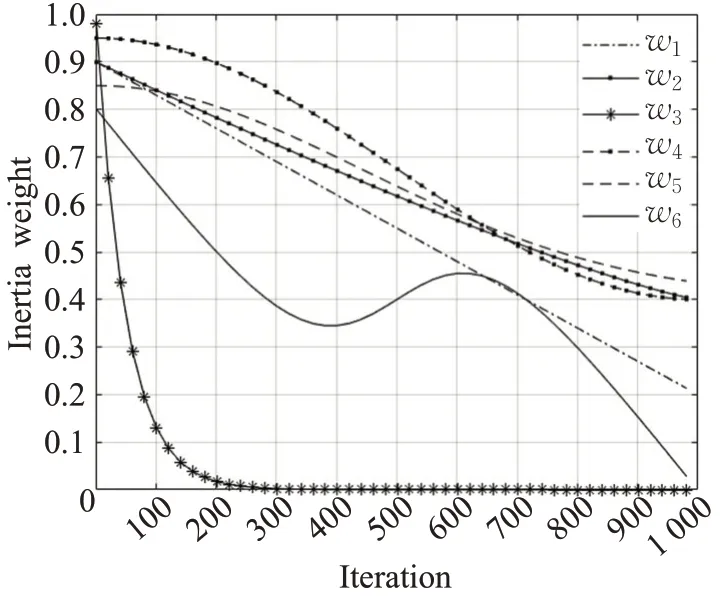
图4 不同方案的惯性权重Fig.4 Inertia weight of different ideas

选取了表2中的部分测试函数，采用控制变量法设置其他相关参数均相同，种群规模为50，迭代优化次数T=1 000，维度D=30，加速系数c1=c2=2。不同惯性权重w的方案在相关测试函数中表现如图5～图8所示。

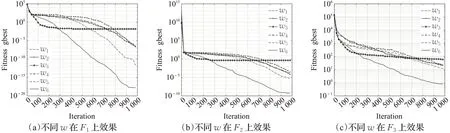
图5 不同惯性权重在F 1、F 2、F 3上的效果Fig.5 Effect of different inertia weight on F 1,F 2,F 3

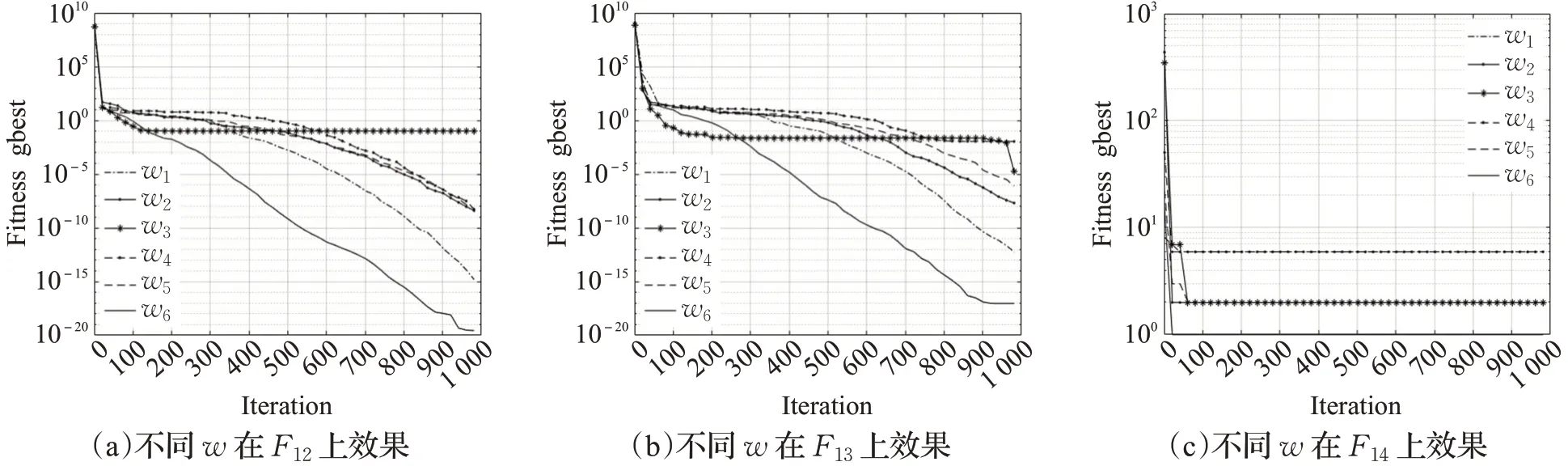
图8 不同惯性权重在F12、F 13、F14上的效果Fig.8 Effect of different inertia weight on F 12,F 13,F 14

实验结果分析：在F1、F2、F5、F6、F7、F9中，由于惯性系数w3曲线为幂函数骤降，在前期获得了较快的收敛速度，但是在后期由于其系数值较小且接近于0，则在迭代中弱化了惯性影响带来的优势，逐渐失去了寻优能力最终效果较差。惯性系数w1、w2、w4、w5从收敛速度和最终结果来看较为普通，整体表现接近。而本文提出的非线性递减方案w6综合了w3的优势，如在F3、F4测试中，前期系数值较大有利于提高算法的全局搜索能力[16]；在中期实现了惯性系数的转折再上升，从F10、F12、F13中可以看出，改进算法增加了粒子的活性，跳跃出当前区域，并扩大了粒子的搜索范围，有效避免了粒子在迭代中期的早熟现象；在后期继续非线性减小提升局部搜索能力[16]，从F3、F6、F10中可以看出，算法仍然拥有良好的寻优精度，且在F14中以最快速度收敛至目标解。

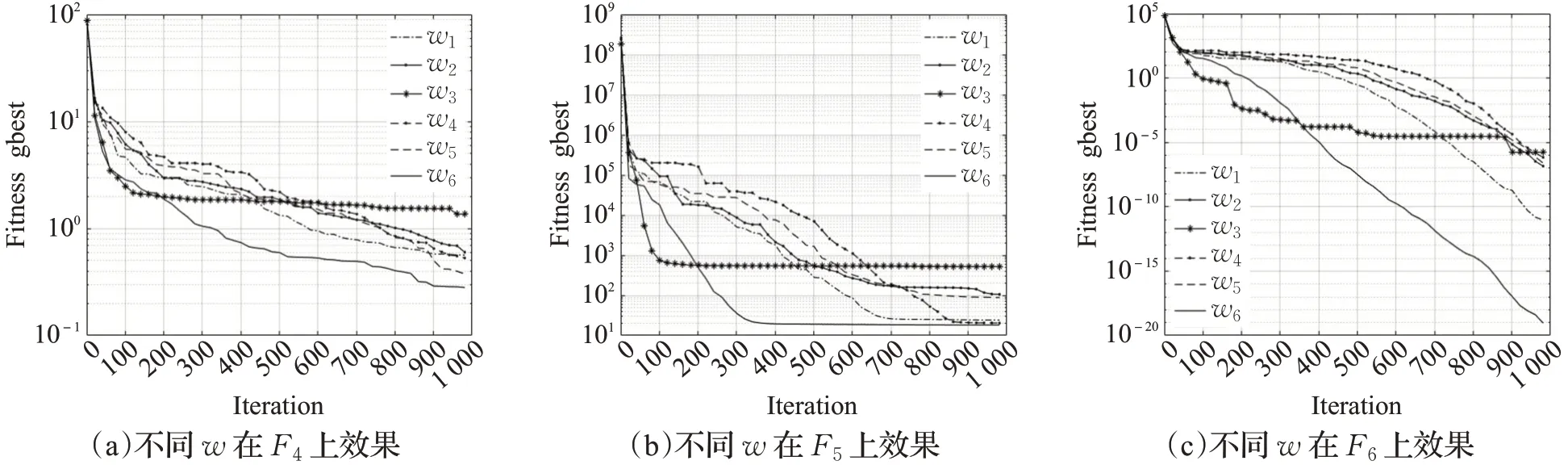
图6 不同惯性权重在F 4、F5、F 6上的效果Fig.6 Effect of different inertia weight on F 4,F 5,F 6

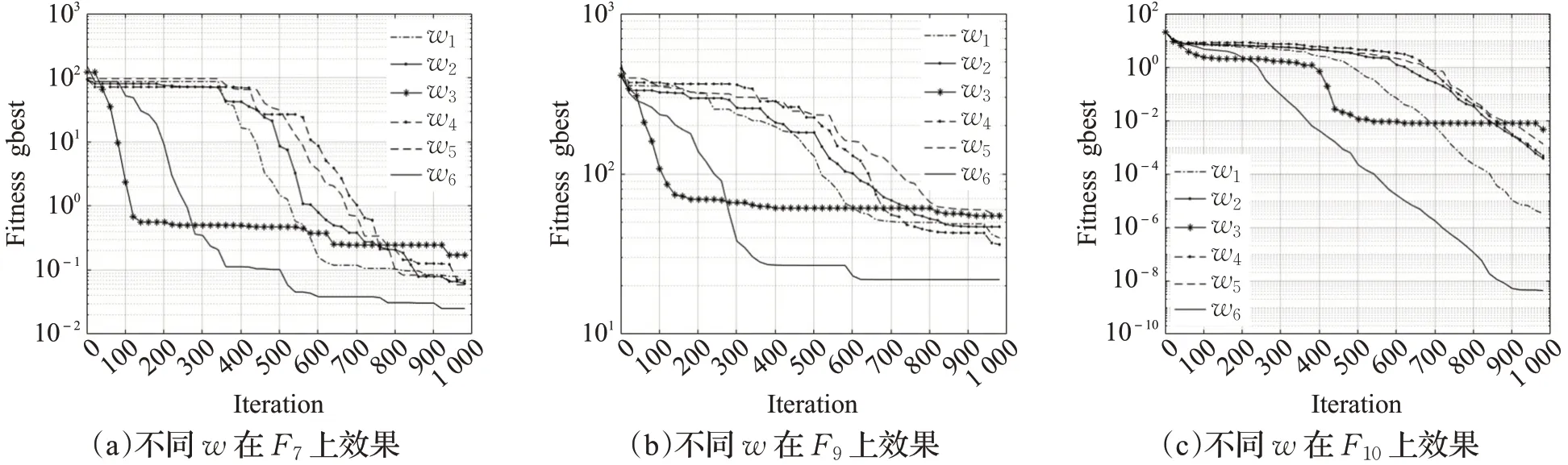
图7 不同惯性权重在F 7、F 9、F 10上的效果Fig.7 Effect of different inertia weight on F 7,F 9,F10

3.3 整体改进对比

综合SCVPSO算法中各项改进策略，为进一步验证其性能和优势，实验选取了基本粒子群算法PSO[7]、linear decay inertial weight PSO（LDWPSO）[8]、adaptive simulated annealing PSO（SAPSO）[14]、PSO based on dynamic acceleration coefficients（PSO-DAC）[22]、a normal distribution decay inertial weight PSO（NDPSO）[23]、exponential decay weight PSO（EXPPSO）[24]来作为对比实验，设置种群数目为100，测试函数搜索范围如表2所示。为保证实验的有效性，各个粒子群算法在每个测试函数上均独立运行30次，统计了在D=30、100时单峰函数和多峰函数上的实验结果如表3～表6所示。

表3 各个算法在D=30单峰函数F1～F7上的结果Table 3 Results of each algorithm on D=30 unimodal function F 1～F 7

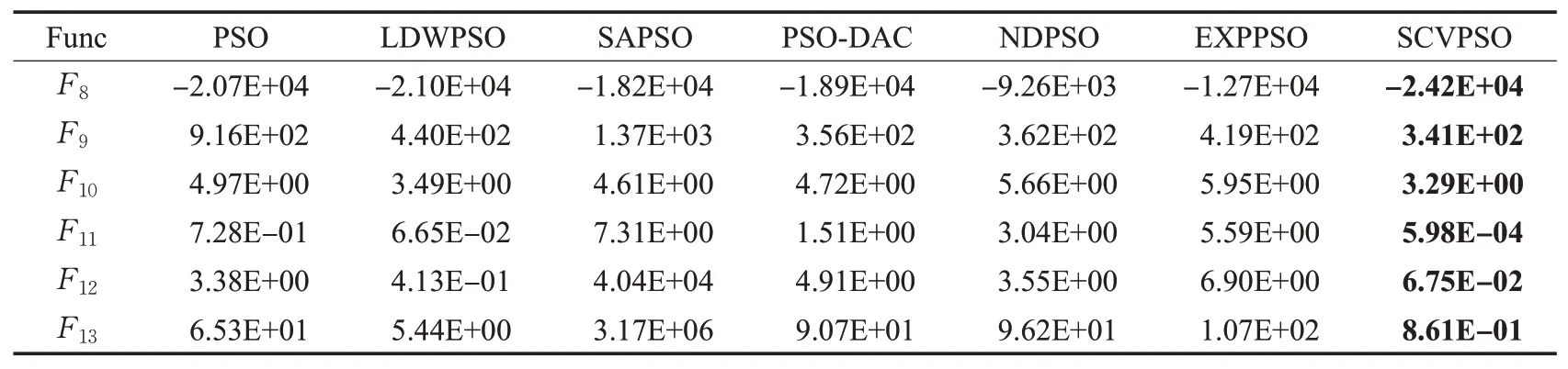
表6 各个算法在D=100多峰函数F 8～F 13上的结果Table 6 Results of each algorithm on D=100 multimodal function F 8～F 13

从表格中可以看出，在D=30时绝大部分单峰函数上，SCVPSO相比于其他算法在收敛精度上具有显著提升，在多峰函数中也具有一定的优势；在提升问题维度D=100后，SCVPSO的寻优结果仍明显优于其他对比算法。其中在多峰函数F9、F13中，提升维度后使粒子变异概率也随之提高，这使得SCVPSO寻优结果重新取得优势，验证了概率变异策略的有效性及改进算法对高维度的鲁棒性。为了更直观地对比不同算法在精度上的差别及其在收敛速度上的表现，实验选取了D=100时部分函数上具有代表性的迭代曲线，如图9～图11所示。

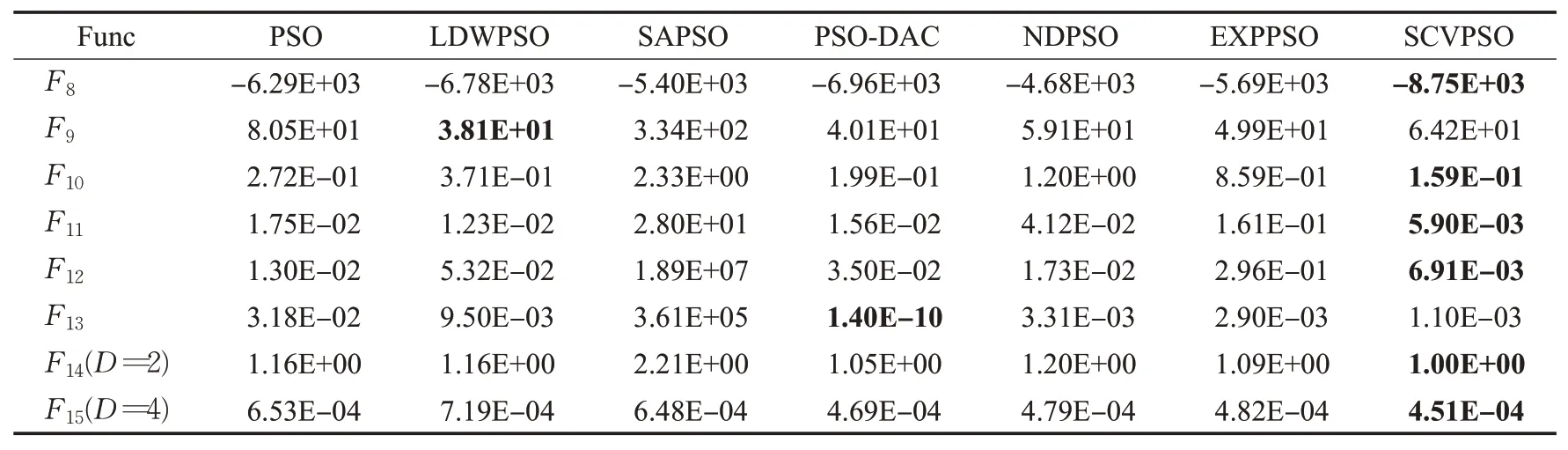
表4 各个算法在D=30多峰函数F 8～F 13上的结果Table 4 Results of each algorithm on D=30 multimodal function F 8～F 13

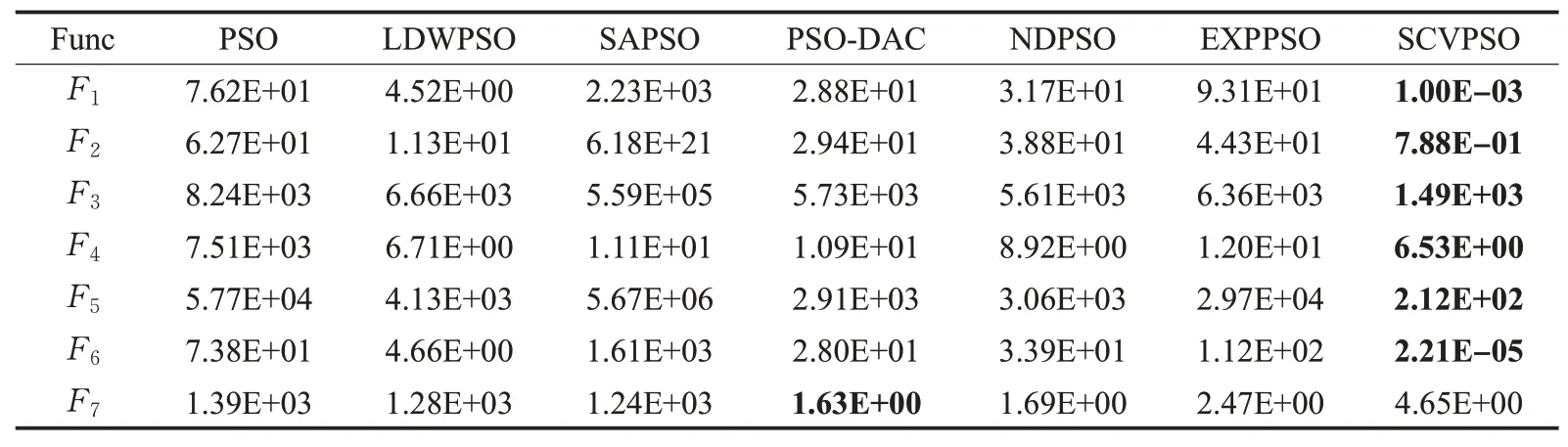
表5 各个算法在D=100单峰函数F 1～F 7上的结果Table 5 Results of each algorithm on D=100 unimodal function F 1～F 7

由图9～图11中可以看出，在函数F3、F5、F11中，迭代中期由于种群陷入局部最优整体曲线停滞，得益于SCVPSO算法中w曲线的二次上升转折，加大惯性影响，跳出了局部区域继续寻优，最终取得了较好的效果，再次验证了该方案w曲线的有效性。在函数F1、F2、F3、F4中迭代后期，SCVPSO仍然不断更新全局最优值，保持着良好的搜索效率。在多峰函数F10、F11、F15中，本文算法能以最快的速度完成寻优任务，充分展现了概率总结性变异在配合新的惯性权重后带来的优势，在增加问题搜索空间的同时也提高了最终求解精度。从不同维度的实验中可以得出，在相同的迭代次数时SCVPSO的适应度值均优于其他算法，且在迭代速度和精度上均具有显著优势。

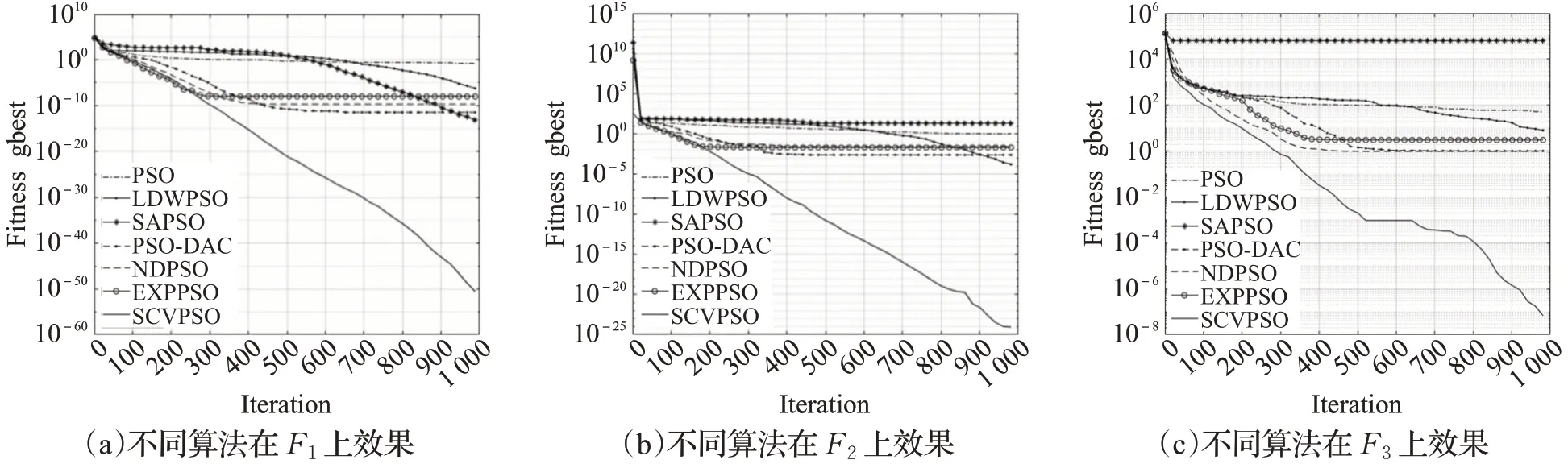
图9 不同算法在F 1、F 2、F 3上的效果Fig.9 Effect of different algorithms on F 1,F 2,F 3

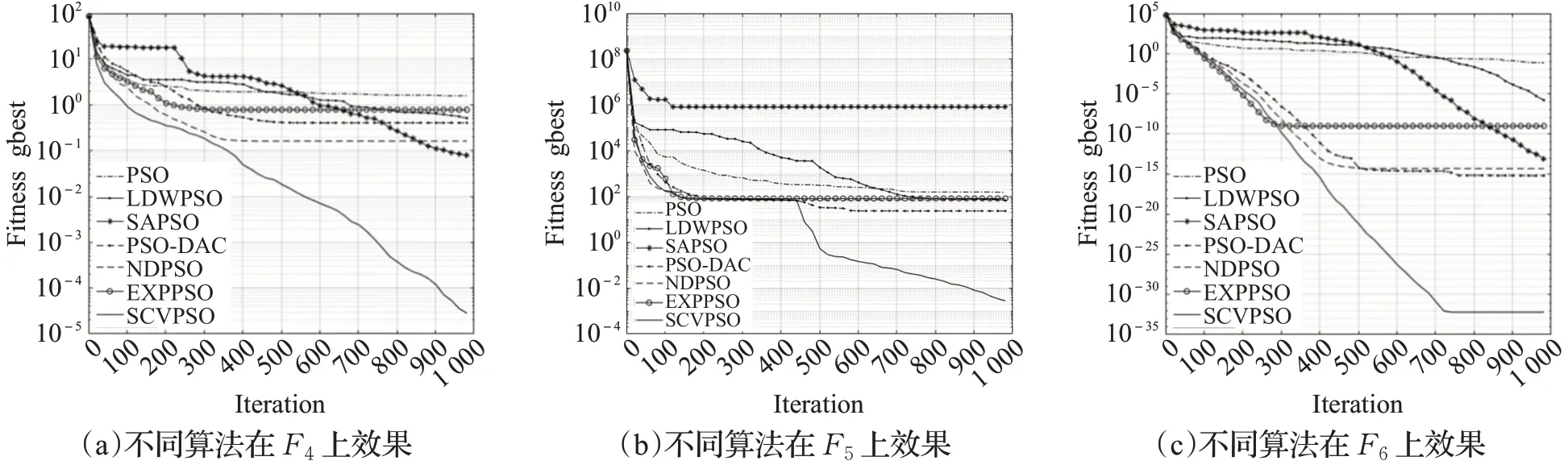
图10 不同算法在F 4、F 5、F 6上的效果Fig.10 Effect of different algorithms on F 4,F 5,F 6

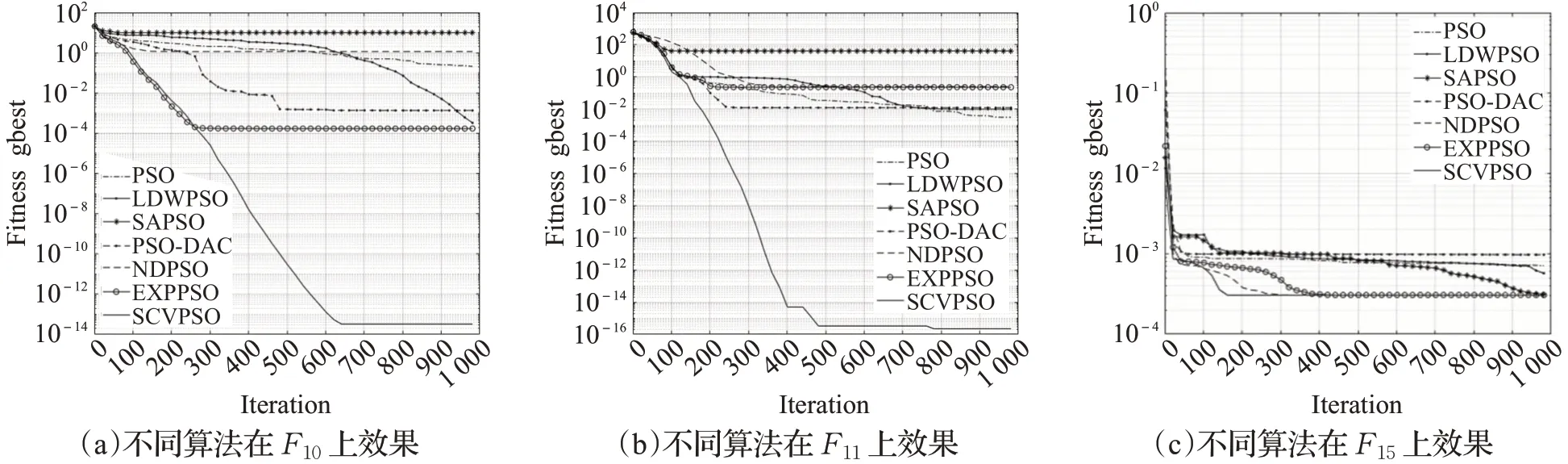
图11 不同算法在F10、F11、F15上的效果Fig.11 Effect of different algorithmson F10,F 11,F15

4 结束语

本文采用非线性转折上升再递减曲线来控制惯性权重随迭代次数的变化，保证了粒子在陷入局部最优后能以最快速度跳出当前区域，扩大搜索空间避免早熟；对筛选的局部粒子作反向搜索处理，提高了种群寻优的效率；引入新的参数scr来分析各个粒子近期求解情况，配合新的惯性权重扩大搜索空间，通过概率单向变异引导粒子指向全局最优，增加了种群中粒子多样性。仿真实验表明，SCVPSO算法在多个单峰函数和多峰函数上，与其他粒子群算法相比具有较高的收敛速度以及求解精度。下一阶段将围绕引入的scr参数对种群进行详细分类，方便对粒子做更进一步的分析研究。