利用邻接结构熵确定超网络关键节点

周丽娜，常 笑，胡 枫

1.青海师范大学 计算机学院，西宁 810008

2.青海省藏文信息处理与机器翻译重点实验室，西宁 810008

3.藏语智能信息处理及应用国家重点实验室，西宁 810008

随着网络科学的蓬勃发展，人们对复杂系统及复杂网络有了更深入的了解，现实世界中大多数系统都可以抽象为复杂网络。而人们对复杂网络的研究已经从宏观层面转变为微观层面（节点、链路）去解释不同网络所具有的不同特征[1]。节点作为网络中最小的单元，在不同的现实网络中起着不同的作用。有效且高效地识别与大规模网络的特定动态相关的关键节点将使人们能够更好地控制流行病的爆发、抑制疾病扩散[2]、精准投放商品广告[3]、预测热门研究成果、发现重要致病基因[4]、寻找恐怖分子头目等等。因此，识别网络中的重要节点至关重要。

随着信息化时代的到来，网络规模不断扩大，网络结构变得复杂多样，基于普通图的复杂网络[1，5-6]已经不能很好地描述真实网络以及复杂系统的各种特性，因此多数学者将视角转向了基于超图的超网络[7-9]。目前，超网络的研究大都基于超网络模型的构建及现实世界的超网络特性研究。Wang等[10]构建了一种超网络动态演化模型，该模型每次增加若干个新节点，并与原网络中已存在的一个旧节点优先连接生成新的超边。胡枫等[11]给出了另一种超网络演化模型，该模型的增长机理与文献[10]模型相对偶，并将BA网络视为该模型的特例。Suo等研究了超网络中信息动态传播问题[12]，并且根据超网络的演化模型分析了供应链网络的演化机制[13]。郭进利研究了非均匀超网络中标度率涌现问题[14]。卢文等[15]构建了节点超度分布具有双峰特性，层间采用随机方式连接，层内采用三种不同类型的双层超网络模型。刘胜久等[16]结合超网络维数与网络能量，提出了超网络能量，论证了超网络的超网络能量与图的网络能量之间的内在关联，并分析了超网络能量的若干性质。马涛等[17]构建了基于加权超图的产学研合作申请专利超网络模型，并分析其拓扑结构。陆睿敏等[18]基于超网络理论构建了上海公交超网络模型，分析了该模型的鲁棒性，从而对城市交通规划与设施管理具有指导意义。而在超网络拓扑结构方面的研究则相对较少，利用超网络拓扑结构指标计算超网络关键节点的研究则更少。Estrada等[8]扩展了复杂网络中子图中心性和聚类系数的定义到超网络上，并用这两种指标识别出了三类现实超网络中的核心节点。胡枫等[19]利用复合参数的方法识别出了蛋白复合物超网络中的关键蛋白。王雨等[20]从超网络角度出发研究了科研合作中的作者的重要性问题，并提出了重要度指标D′，能够较好地识别出科研合作超网络中的关键节点。单而芳等[21]讨论了超网络中心性测度的一类方法——广义Position值方法。孙琳等[22]基于超网络理论对上海交通轨道网络进行识别关键节点的实证研究。

近年来，信息熵[23]广泛应用于复杂系统与复杂性理论，Fei等[24]将信息熵应用到复杂系统的关键节点识别中，并取得了良好的效果。黄丽亚等[25]依据网络节点在K步内可达的节点总数定义了K-阶结构熵，并从三个方面评价网络的异构性。胡钢等[26]通过计算网络各节点的邻接度得到节点信息熵，利用节点信息熵的大小表征节点在网络中的重要性。李懂等[27]融合了度与k核迭代次数并利用熵权法计算度和k核迭代次数的权重，从而识别节点的重要性。王倩等[28]将软件动态执行过程抽象为有向复杂网络结构模型，并结合结构熵提出了软件动态执行关键节点挖掘算法。迄今为止，针对邻居结构熵的研究都是基于普通图的复杂网络上的应用研究，而缺乏基于超图的超网络上的定义及应用研究。网络的拓扑结构决定网络的功能和性质，复杂网络的拓扑结构为普通图，即一条边连接两个节点，而超网络的拓扑结构为超图，超图中的超边可连接任意多个节点，更切合现实网络的复杂、多元、群聚特性。因此，为刻画真实数据集的多元群组关系，以综合视角研究复杂的现实系统，学者们将研究重点逐渐从复杂网络转向超网络。超网络分为基于网络的网络（supernetwork）和基于超图的网络（hypernetwork）。Estrada等最先在文献[8]提出拓扑结构为超图的网络称为超网络（hypernetwork）。超图是普通图的扩展，普通图中的“边”只能连接两个节点，而超图中的“超边”可连接任意多个节点。节点连接的超边数量称为节点的超度。基于超图的超网络，由于结构简单、表示多元关系清晰明了，更适合刻画现实世界的综合、群组、多元结构，这种独特优势使其获得越来越多的重视。因此，本文在基于超图的超网络上，分析超网络中节点的重要性的识别方法。网络中的节点相互影响，只考虑度或超度值，会损失直接或间接邻居对节点的影响；考虑全局节点会增加算法的复杂度，且效果不一定很好，因为，节点的重要性不仅与自身的影响力有关，还与邻接节点的重要性密切相关。如在以作者为节点，合作发表的论文为超边构造的科研合作超网络中，一个人的重要性与个人所发表的论文数量（即节点的超度值）有关，还与合作者的影响力（即邻居节点的超度）有关，通常情形下，作为合作者的导师的影响力往往会波及个人；一个网页的重要性与指向它的权威网页存在重大关系等。

基于以上考虑，本文提出用邻接结构熵识别超网络中的关键节点，通过研究节点及其直接与间接节点间的关系，利用节点信息熵刻画不同节点在超网络中的重要性。其优势在于不仅考虑了节点自身的性质，也融合了邻居节点的影响力，且由于该算法只利用节点的局部属性，故其复杂度较低。为了验证此算法的适用性及正确性，本文收集了《物理学报》2012—2020年间发表的论文及作者信息，构建了一个作者为节点，合作发表的论文为超边的科研合作超网络。实证分析结果表明，本文提出的基于邻居结构熵识别关键节点的算法可以精准地识别超网络中的重要节点。

1 相关知识

1.1 超网络相关概念

超图概念最早是Berge[29]提出的，设V={v1,v2,…,vn}是一个有限集。若ei≠φ(i=1,2,…,m)，且则称二元关系H=(V,E)为超图。其中V的元素称为超图的节点或顶点，E={e1,e2,…,em}是超图的边集合，集合E的元素ei称为超图的超边。超图H=(V,E)的邻接矩阵A(H)是一个N×N的对称方阵，其元素aij为同时包含顶点vi和vj的超边数量，对角线元素为0。关联矩阵B(H)是一个N×M的矩阵，如果顶点vi包含在超边ej中，则bij=1，否则为0。超网络中节点度等同于普通图中度的定义，即节点的连边数，即，简记为ki。节点超度是包含该节点vi的超边数属于同一条超边中的节点为超图量，即中的邻接节点。Estrada等[8]提出了超网络中子图中心性的计算公式，即其中，λj是超网络H中邻接矩阵A的特征值，U=(uij)N×N是一个正交矩阵，且每一列都是特征值λj对应的特征向量。

1.2 信息熵

信息熵于1948年由Shannon提出，信息熵的优点是能够从系统样本点的不确定性出发，利用概率与统计方法，表征样本空间所体现的系统无序化程度，该方法能够很好地衡量网络节点的重要性。

1.3 网络结构熵

熵是系统的一种无序度量，用来描述一个系统内所有元素的状态总和。网络熵主要从网络结构和网络信息收容能力（即网络能够收取容纳信息规模的能力）来定义。吴俊等[30]利用网络节点的度与所有节点度值总和的比值来度量节点的差异性，提出了基于网络节点度来定义网络节点的重要性程度，最后通过网络节点的重要性程度定义网络结构熵。

定义1假设网络中节点vi的度为ki，则其重要度可以定义为[30]：

对于ki=0的节点不作考虑。定义网络结构熵[30]：

1.4 邻接信息熵

定义2（节点邻居概率函数）为了描述不同节点的邻居节点对节点的影响力大小，节点邻居概率函数定义如下：

其中，ki为节点vi的度值，Qi为节点vi的邻接度，通过以上改进，在复杂网络中，重要节点的识别计算公式如下：

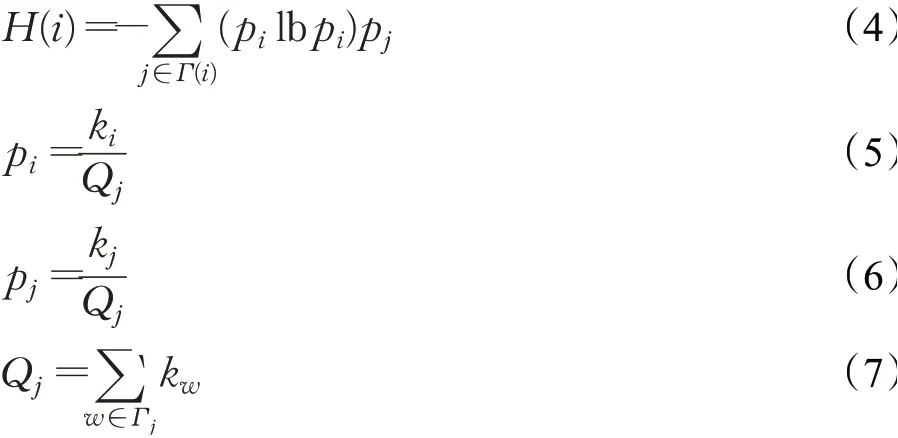
其中，pi为节点vi的概率函数，pj为节点vj的概率函数，Γi为节点vi邻居节点的集合，Γj为节点vj邻居节点的集合。

2 邻接结构熵

超网络中节点超度只能反映节点被包含的超边的数量，不能很好地反映节点与其他间接邻居节点的连接情况，为此，本文引入节点邻接超度的定义，在此基础上给出超网络中的邻接结构熵概念，通过邻接结构熵值识别超网络中的关键节点。

定义3（邻接超度）为了更准确地反映超网络中邻居节点对该节点的影响，通过邻接节点的重要性确定目标节点的地位。目标节点的邻接超度定义如下：

其中，d H(j)为节点i的超度值，R(i)为节点i的邻接节点集合。

定义4（重要度函数）为了描述超网络中不同节点在其邻居节点中被选中的可能性大小，定义超网络中节点的重要度函数：

其中，DH(i)为超网络中节点i的邻接超度。

定义5（邻接结构熵）结合邻接超度与网络结构熵定义，将超网络中计算单个节点vi的邻接结构熵定义如下：

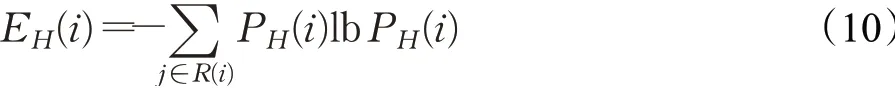
其中，PH(i)表示超网络中节点的重要度函数。

根据以上定义可知，超网络中的邻接结构熵不仅与节点的超度有关，还与邻接节点的超度有关。若节点包含在多条超边（即多个团队或族内）中，其重要性不仅跟自身有关，也与其邻接节点（即团队成员）的重要性有关。利用邻接结构熵值的大小，表示节点在超网络中的重要性。邻接结构熵值越大，节点越重要，表明该节点隐含的信息的价值越高。

本文实例为Estrada等在文献[8]中的竞争复杂网络与超网络对比图验证本文算法的正确性。在竞争网中，节点表示物种而链表示物种之间的营养关系。如图1所示的竞争网络及对应的竞争超网络图[8]。在竞争网中，当且仅当联系的物种在食物网中有共同的猎物时，两点直接连边。在竞争图中，仅仅知道两个联系的物种之间有共同的猎物，但并不知道为共同猎物竞争的整个物种群的构成情况。在竞争超网络中，节点为物种，竞争同一猎物的物种在同一条超边中，节点所竞争的猎物与邻居节点竞争的猎物一目了然。该竞争超网络由8个节点和3条超边组成，即8个物种竞争3种猎物，竞争关系明确清晰。节点的重要性也易识别。表1为此超网络超度、子图中心性及本文算法提出的邻接结构熵的排序结果。

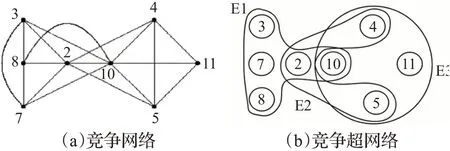
图1 竞争网络与竞争超网络Fig.1 Competitive network and competitive hypernetwork

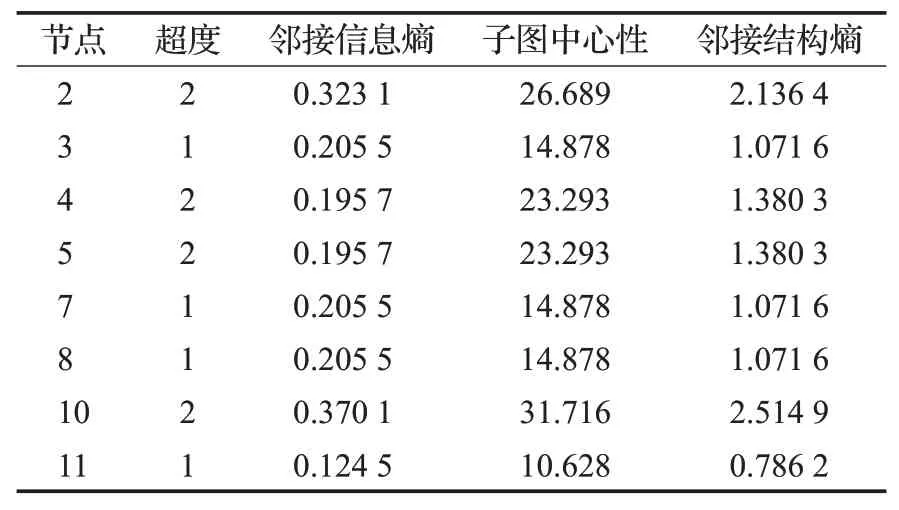
表1 竞争超网络各指标Table 1 Index of competitive hypernetwork

由表1知，超度不能很好地区分各节点的重要性，根据邻接信息熵、子图中心性及邻接结构熵知，节点10是此竞争超网络的重要节点。其子图中心性和邻接结构熵的值均远远大于节点2。节点10代表的物种发生在竞争数量最多的群体E1和E3中，分别有5个和4个竞争者，又因为它在子结构中参与同时涉及竞争群和外部群的物种，这使得此物种难以生存。排名第二的关键节点是节点2，它参与E1和E2组；接下来是节点4和5，它们参加E2和E3群体的竞争。

基于邻接结构熵计算节点重要度的算法如下：

步骤1对于超网络H=(V,E)，根据其邻接矩阵A(H)计算给定超网络H中节点i的超度d H(i)及邻接超度

步骤2按照重要度函数式计算概率函数PH(i)。

步骤3根据式，计算节点i的邻接结构熵；重复步骤2至3，直到计算出所有节点的邻接结构熵。

步骤4根据各节点的邻接结构熵大小对节点进行排序。

超网络H中，节点个数为V，超边数量为E，文献[8]提出的超网络中子图中心性的时间复杂度为O(V2)。复杂网络中，文献[30]利用节点的度计算网络结构熵的时间复杂度为O(V)，文献[28]利用节点及节点的邻居节点的度计算邻接信息熵的时间复杂度为O(V2)。本文算法利用公式（4）、公式（5）计算超网络中每个节点的邻接结构熵，算法时间复杂度为O(V)。本文算法相比其他算法，时间复杂度更优。

3 实验结果与分析

3.1 复杂网络与超网络比较

为了比较邻接结构熵在复杂网络和超网络中的异同性，本文在Estrada文献[8]的竞争网络和竞争超网络中进行邻接结构熵的重要度比对，并与网络结构熵和邻接信息熵进行比较。结果如图2所示。

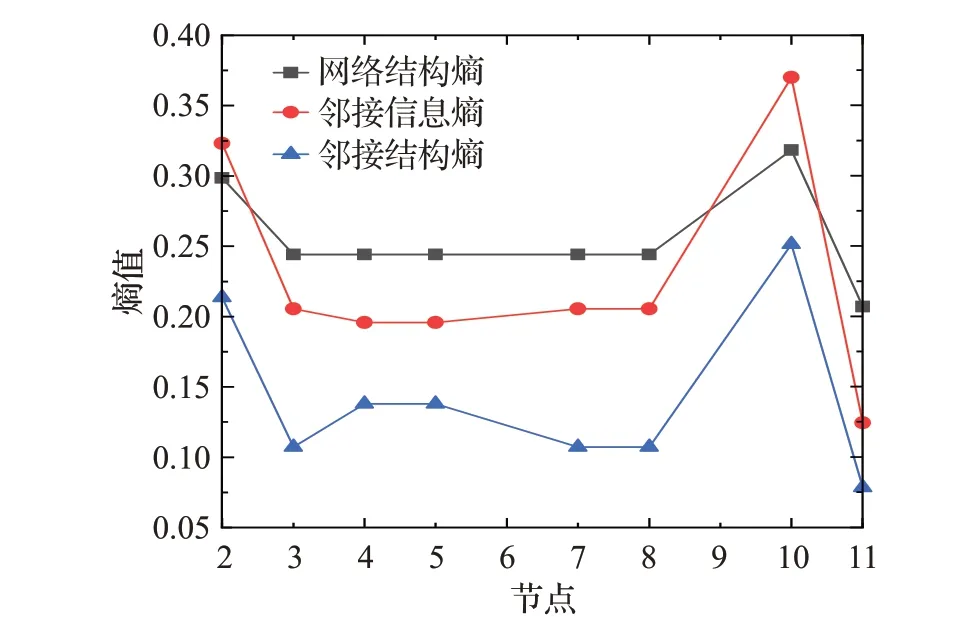
图2 复杂网络和超网络的熵值Fig.2 Entropy of complex networks and hypernetwork

从图2可知，由复杂网络的网络结构熵识别出节点10为重要节点，与超网络的邻接结构熵识别出的关键节点相同。但是，由于复杂网络中各节点的度值大致相同，导致根据网络结构熵与邻接信息熵得到的节点的粗粒化程度较高，难以区分度值相同的节点的重要性。而超网络中也存在某些节点超度值相同的情况，但超网络的邻接结构熵则能够较好地区分出各节点的重要性。

3.2 数据来源

为了进一步验证该算法的正确性，本文以《物理学报》为例，选取发表时间为2012年1月1日—2020年9月10日的文献记录。其中涵盖了16 158位不同的作者撰写的5 338篇论文，基于此数据集构建科研合作超网络模型，该模型包含16 158个作者节点和5 338篇论文超边。其中独立发文的作者有138人，仅占2.5%，故大部分论文由多位作者共同合作完成，且绝大多数论文由3～6个作者合作完成。

3.3 实验结果分析

将本文算法应用到上述超网络中，得到各个作者的邻接结构熵如图3（a）所示，图3（b）为各作者的超度值，即作者发表论文的数量。横轴表示节点编号；纵轴分别表示节点的邻接结构熵和节点超度值。由图3可以看出，大部分节点的邻接结构熵和超度值均处于区间[1，5]。由此可知，大部分作者在其领域内的影响力较低，并且大部分作者仅发表了1～5篇论文。

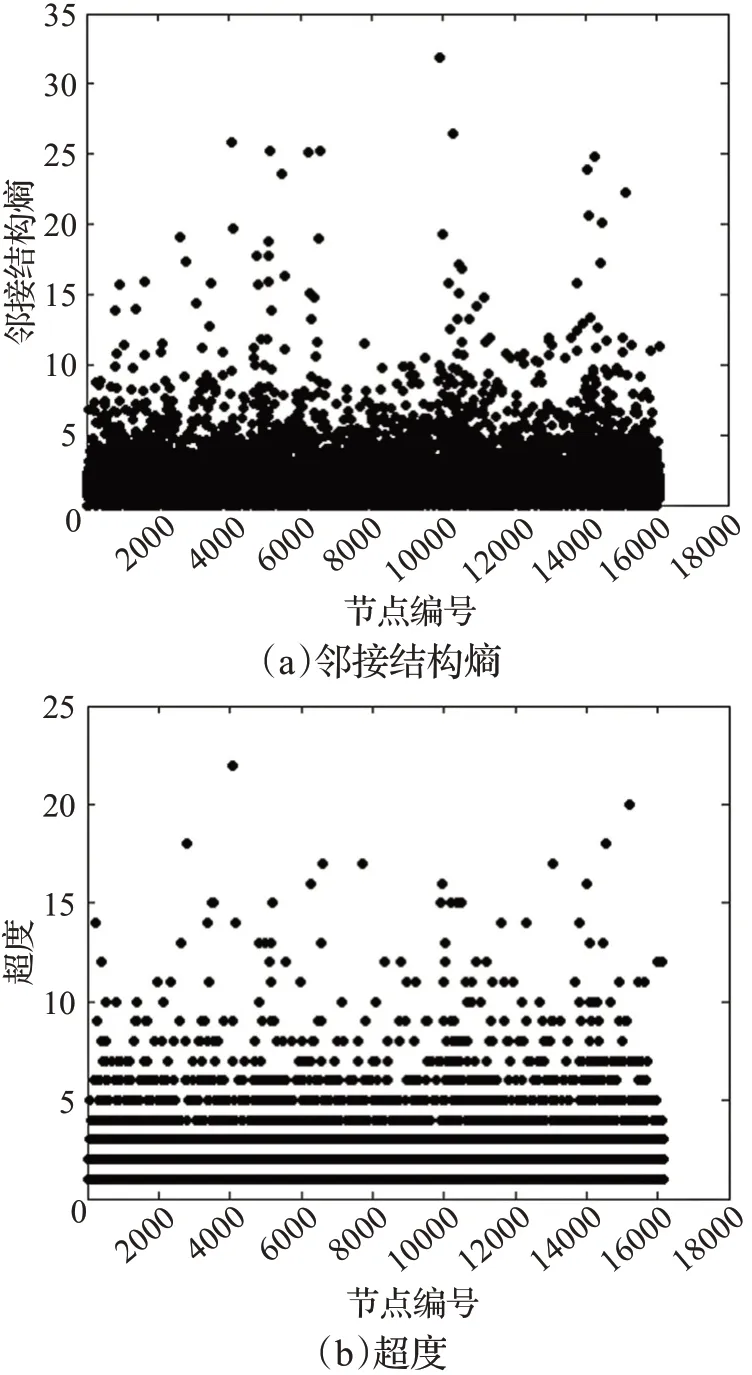
图3 所有节点的邻接结构熵及超度值Fig.3 Adjacent structure entropy and hyper-degree value of all nodes

由图3知，各节点所处的位置相对分散，层次分明，颜色越深的地方，节点分布越密集。从图3（a）可知，节点9941的邻接结构熵值远远高于其他节点，此节点为超网络的关键节点。从图3（b）可以看出，节点所处位置分布规律，且均匀地分布在超度值为1～5的位置，然而超度值相同的节点较多，这类节点重要性相同，故超度的粗粒度高于邻接结构熵。因此，邻接结构熵能够有效地识别出超网络中的关键节点。通过对这16 158位作者的邻接结构熵进行排序，得到排名结果前20的作者及其相应指标，结果见表2。由表2知，节点9941的邻接结构熵最为突出，为31.83，属于重要作者，是该科研合作超网络的关键节点。通过对节点的超度进行排序，得到超度值最大的节点为节点4057，其超度值为22；但其节点度为77，表明与节点4057合作的作者的超度值均较大，因此，他的邻接超度值较大。通过分析作者自身发文量占与他合作的作者的发文量的比例，得出此比例小于节点9941，故其邻接结构熵小于节点9941的邻接结构熵。因此，节点4057再次参与合作论文的可能性相对较小。而节点9941的合作作者人数为102，相比较于节点4057较多，但其邻接超度较小，故再次邀请节点9941参与合作论文的可能性较大。节点9941发表的论文中署名为第一作者的论文偏多，而节点4057的署名均位于末尾，因此，节点9941共同合作发表论文的次数比节点4057的可能性大，节点9941更有合作潜力。

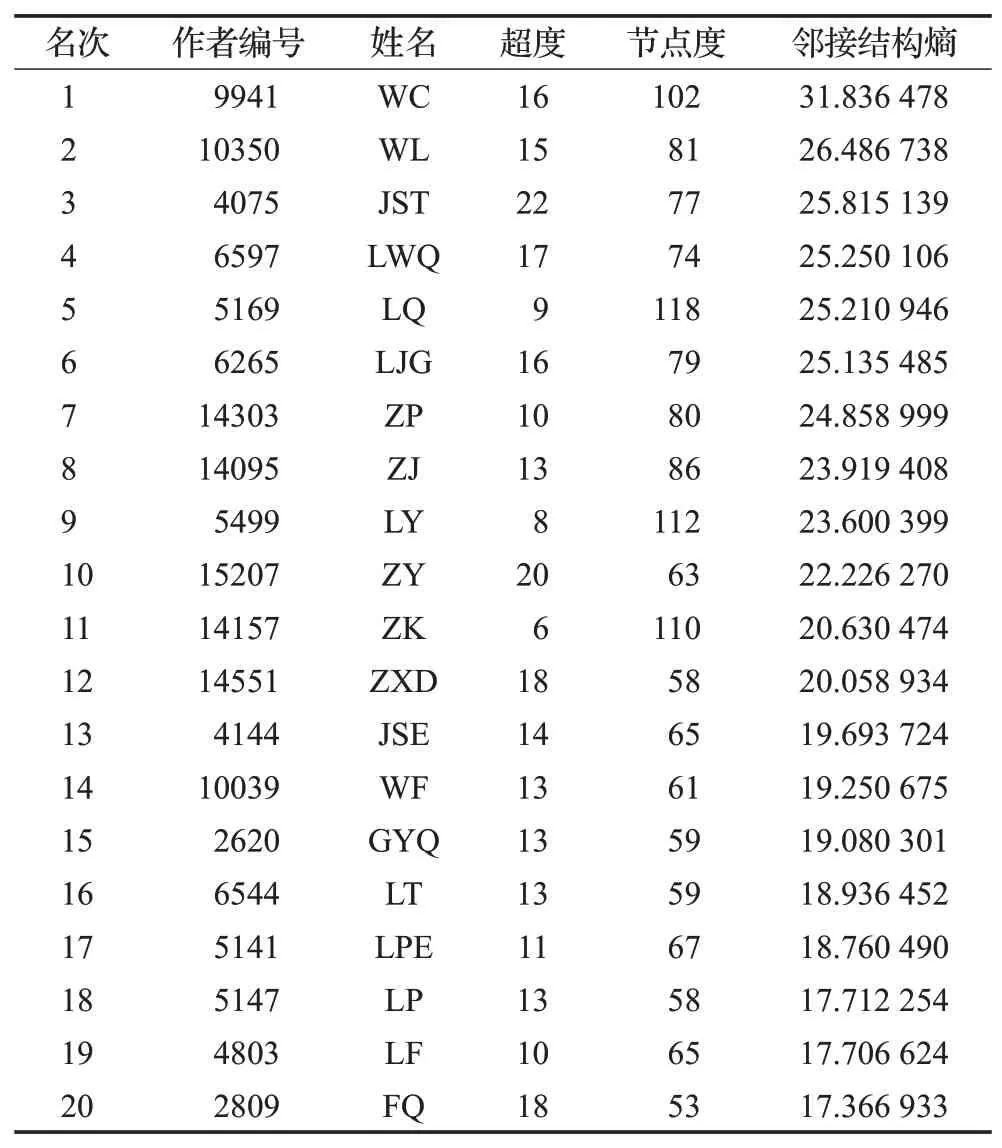
表2 邻接结构熵排名前20的作者及相应指标Table 2 Top 20 authors of adjacency structure entropy and their corresponding indicators

排名第二的关键节点是节点10350，其邻接结构熵为26.48，超度值排名第8，该节点的邻居节点个数为81，位于第14位。其中，该作者节点的大多数论文由3～5名作者共同合作完成，此节点与邻接结构熵排名第一的节点9941生成一条超边。此节点的邻居节点超度值较小，选择该作者共同合作论文的机率较大，故此节点的邻接结构熵排在第二位。进一步，比对超度、邻接结构熵、节点度的排名情况，如图4所示邻接结构熵排名前20名作者的度、超度。

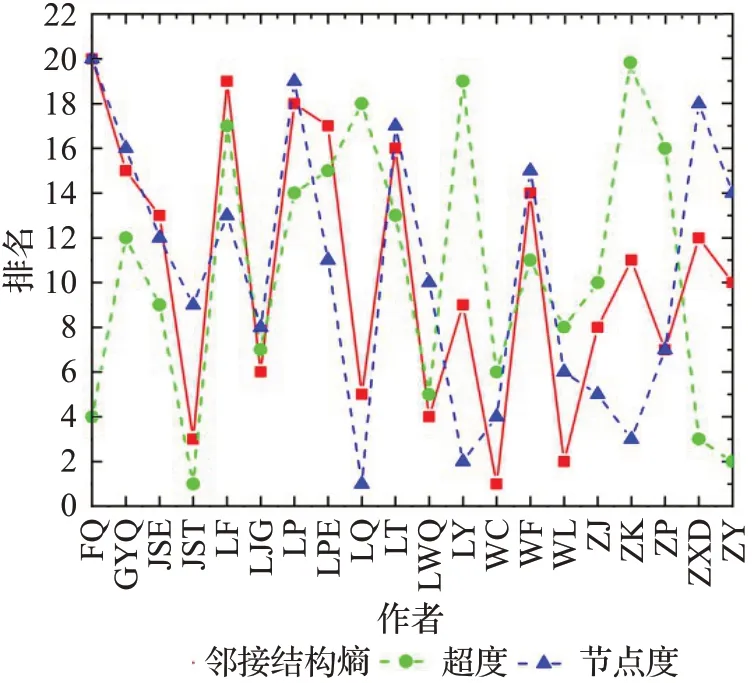
图4 作者各指标的排名Fig.4 Ranking of each index

图4横轴表示作者，纵轴为三个指标的名次排名。方块表示邻接结构熵，圆圈表示超度，三角表示节点度。在此超网络中，超度反映作者的发文量，邻接结构熵反映该作者再次发表论文的可能性，也就是作者在其领域内的影响力，作者合作发表论文的发展潜力，而节点度反映作者的合作人数。根据节点度排名，排名第一的节点5169，其节点度为118，但其超度值仅仅为9，其邻接结构熵值排在第5位。该作者发表的论文中有一篇论文《中国散裂中子源反角白光中子束流参数的初步测量》与86位作者共同合作完成，导致该作者的节点度最大，因此，仅利用节点度衡量网络节点的重要性并不准确。

此数据集收集了2012—2020年间各个领域、各个方向的论文及作者，故识别的关键作者共同发表论文、形成良好的交流环境并形成对应领域内团体的可能性很小，但识别出的重要作者均为各领域内具有较大影响力的关键人物。例如，邻接结构熵排名前三位作者的研究领域如下，节点9941的H指数为46，研究领域是摄影测量与遥感；节点10350的H指数为48，研究领域是环境工程；节点4075的H指数为43，研究领域是光学。

最后，利用准确性评价指标AUC指标，从整体上衡量算法的准确度。对网络中各节点的重要性排序，当节点分配到不同的排序值越多，算法划分节点重要性更清晰。即AUC值越大，算法准确性越高。

表3为超度和邻接结构熵的AUC指标。由表3可知，邻接结构熵的AUC指标略高于超度的AUC指标，故进一步验证了邻接结构熵可以高效、准确地识别超网络中的关键节点。

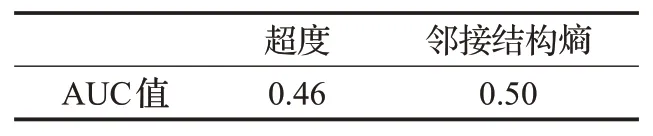
表3 AUC指标Table 3 AUC index

4 结语

识别网络中的关键节点不仅能够分析网络的拓扑结构，还能预测节点的实际影响力。而网络中节点的重要性不仅与节点自身性质有关，也与其邻居节点的重要性有关。本文结合邻接超度与网络结构熵，提出了基于超网络的邻接结构熵，用于识别超网络中的关键节点。并将此指标应用于竞争超网络，准确地得到了该超网络的关键节点。其次，分析比较复杂网络与超网络，得到的关键节点均为节点10。最后，本文从知网收集了《物理学报》2012—2020年间的作者及其发表的论文，构建了科研合作超网络，并将超网络中的邻接结构熵应用于该数据集中，实验分析证明，该算法能够准确高效地识别出超网络中的关键节点。本文为今后预测超网络中的关键节点、识别有影响力的学者，以及研究超网络拓扑结构提供了一种行之有效的方法。