龙格库塔程序的似然蜕变关系识别方法

文双红，阳小华，闫仕宇+，刘 杰，李 萌，冯晋涛

(1.南华大学 计算机学院，湖南 衡阳 421001；2.南华大学 中核集团高可信计算重点学科实验室，湖南 衡阳 421001；3.南华大学 湖南省智能装备软件评测工程研究中心，湖南 衡阳 421001；4.中国核动力研究设计院 核反应堆系统设计技术重点实验室，四川 成都 610041)

0 引 言

蜕变测试技术是缓解“测试Oracle”问题的有效方法之一，其成本效益好[1,2]。蜕变关系是蜕变测试中至关重要的组成部分，因为蜕变关系既为生成衍生测试用例做了铺垫[3]，又为判断程序是否正确提供依据。阳等通过分析科学计算程序的研发过程，建立了物理、计算和代码模型蜕变关系的层次分类模型[4]，再由代码模型蜕变关系层的程序输入、输出运行轨迹的分析中，引出了似然蜕变关系的定义[5]，由似然蜕变关系结合领域知识可以进一步验证得到蜕变关系。

近年来在似然蜕变关系识别上，已有专家学者开展各项研究。Su等[6]分析转换方法的输入值前后特性动态推导似然蜕变属性，利用同一方法的不同版本检测到的不同蜕变属性来发现潜在缺陷；Troya等[7]创建蜕变关系模式集合来对元模型进行转换，进而发现回归测试、增量转换和语言迁移模型转换程序中的错误；Zhang等[8]利用粒子群算法搜索多项式形式的似然蜕变关系；Sun等[9]根据数据变异算子定义输入模式，再由输出映射规则推导产生数值计算程序的蜕变关系；UK等[10,11]将程序代码片段转换控制流图和特征值，预设的蜕变关系作为标签值，利用机器学习的方法预测蜕变关系；阳等[5]借鉴动态不变量的思想，提出一种发现似然蜕变关系的算法框架。李[13]利用问题域和函数拟合知识，提出一种数据驱动的启发式似然蜕变关系识别方法。以上研究在特定应用领域取得一定成就，对于推动蜕变测试技术的发展具有重要意义，但缺乏系统性和适用性，有待继续深入研究。

邱等[12]已将蜕变测试应用到常微分方程程序，但是没有描述如何系统地产生蜕变关系。因此，本文针对常微分方程的龙格库塔算法程序，提出了一种基于SPSS的似然蜕变关系识别方法。SPSS工具是一款成熟的统计应用软件，在数据拟合、分析和挖掘等方面具有优势。本文采取静态分析的方式识别程序有意义的输入模式，通过预设丰富的形式，利用SPSS工具动态挖掘满足特定输入模式的测试数据序对的输出模式，似然蜕变关系为识别真正的蜕变关系提供启发信息。

1 基本概念

1.1 蜕变关系

定义1 蜕变关系[5]：假设程序P用来计算函数f，x1,x2,…,xn(n>1)是f的变元组，且f(x1),f(x2),…,f(xn)是它们所对应的函数结果。若x1,x2,…,xn之间满足关系r时，f(x1),f(x2),…,f(xn)满足关系R，即

r(x1,x2,…,xn)→R(f(x1),f(x2),…,f(xn))

(1)

则称(r,R)是P的蜕变关系，其中，r为蜕变关系的输入关系，R为输出关系。

显然，如果P是正确的，那么它一定满足下面的推导式

r(I1,I2,…,In)→R(P(I1),P(I2),…,P(In))

(2)

其中，I1,I2,…,In是程序P的对应于x1,x2,…,xn的输入，P(I1),P(I2),…,P(In)是相应的输出。因此，可以通过检测式(2)成立与否来判定程序P的正确性。

例如，三角函数sin程序，Chen等[2]通过人工静态分析sin函数的数学属性推导了10条蜕变关系，如图1所示。以Rsin1来介绍蜕变关系的组成和原理，假设有一输入值为52°，生成一个新的输入值为52°+180°=232°，然后执行程序，判断sin(52°)=sin(232°)是否成立，不成立则说明程序存在错误。

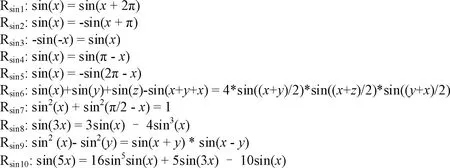
图1 三角函数sin的蜕变关系

1.2 似然蜕变关系

定义2 似然蜕变关系[5]：假设T={(xi,yi)|xi∈D,yi=P(xi),i=1,2,…,n} 是P的运行轨迹，记Tx={xi|(xi,yi)∈T}，若对于任意的xi1,xi2,…,xin∈T,n≪N，都有

r′(xi1,xi2,…,xin)→R′(yi1,yi2,…,yin)

(3)

其中，yi1,yi2,…,yin是xi1,xi2,…,xin对应的输出，称(r’, R’)是P关于T的似然蜕变关系，简称似然蜕变关系，也可以看成是输入模式和输出模式的蕴含式。r′为似然蜕变关系中的输入模式，R′为输出模式。

显然，如果P是正确的，那么P关于x的定义域D的蜕变关系一定是P关于T的似然蜕变关系，反之则不然。因此P的似然蜕变关系对识别P的蜕变关系起到促进作用。

Zhang等[8]预设输入模式为一次多项式、输出模式为一次和二次多项式，将输入模式和输出模式组合为一个多项式，利用粒子群搜索算法从成功的测试用例中求解多项式参数，最后通过筛选得到检错率高的似然蜕变关系，以三角函数sin程序为例，如图2为Apache库下sin程序的多项式似然蜕变关系。

图2 sin程序的多项式似然蜕变关系

2 似然蜕变关系识别方法

2.1 基本框架

现有的自动化的似然蜕变关系识别方法主要通过预设输入模式和输出模式，从成功的测试用例中挖掘具体的输入模式和输出模式来获取程序的似然蜕变关系。但存在预设的关系模式太少、盲目搜索特定方程参数解。因为蜕变关系与待测程序的领域知识密切相关，而输入模式是蜕变关系的前提，有意义的输入模式是衍生测试用例的来源，如果能首先通过静态分析导出其有意义的输入模式，然后生成测试数据，执行程序后的测试输出中再来挖掘其输出关系，则更具针对性，减少了盲目性。

该方法框架如下：

(1)根据输入模式识别规则，静态分析领域知识来识别一批有意义的输入模式；

(2)根据每一条输入模式来生成测试输入数据；

(3)从执行程序的输出结果中，利用SPSS工具挖掘各种类型的输出模式；

(4)最后验证所发现的输入、输出模式，进而得到程序的似然蜕变关系。

该方法的主要过程如图3所示，详细的描述见2.2节。

图3 似然蜕变关系识别方法流程

2.2 识别过程

似然蜕变关系识别方法具体而言，分为4个步骤。

2.2.1 输入模式

似然蜕变关系是由输入模式和输出模式组成的，因此识别过程可以从两个方面考虑，输入模式从特定程序算法层次的背景知识中识别，下面提出了4条规则来指导产生程序的输入模式：

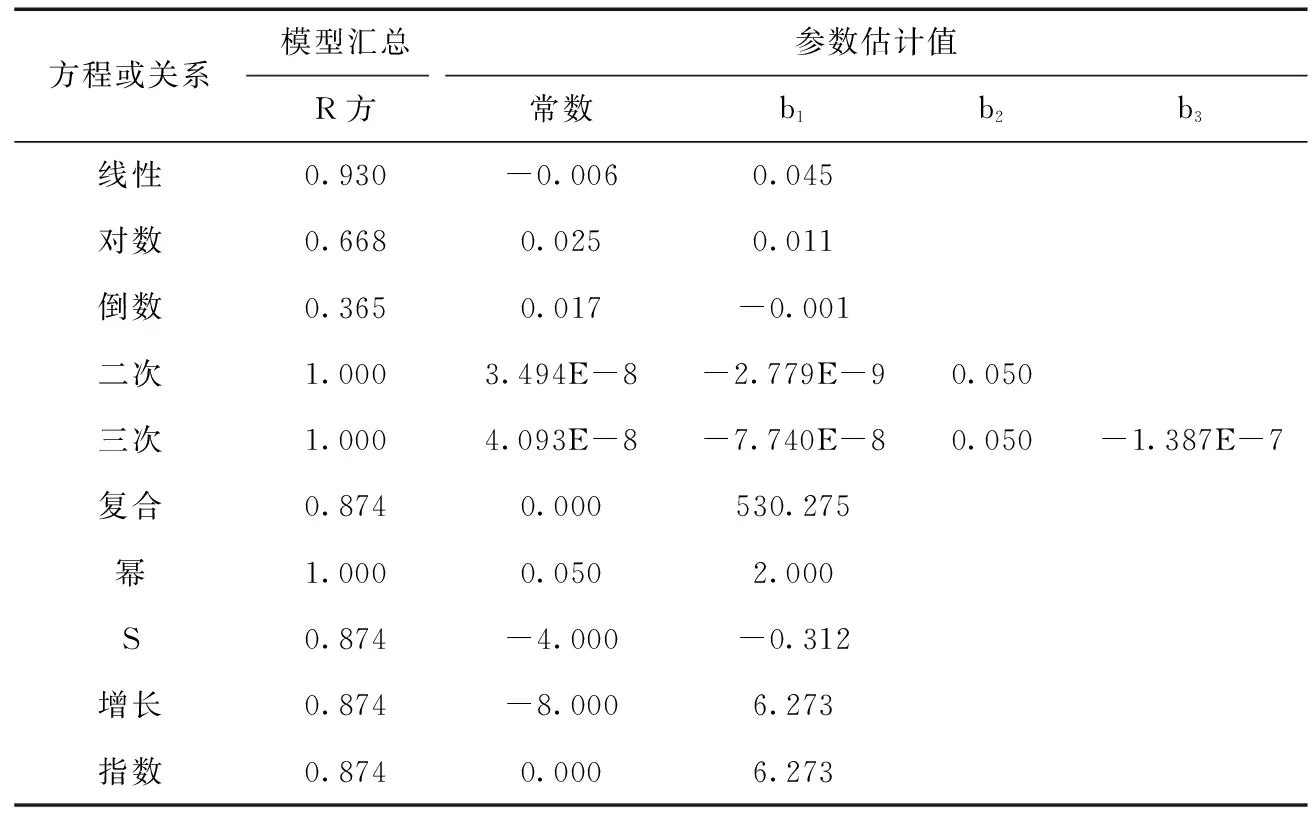
(1)分析算法数值解的性质。需要已知少量算法的原始数据，分析这些数据是否满足数学性质，如单调性、奇偶性、周期性、对称性。设算法求解函数f(x)，若数值解呈单调趋势，分析xi

(2)分析程序预置参数的数值特性。适用于除了生成测试数据外，还与预置参数(如坐标、范围、步长等)相关的程序。进一步分析参数代表的含义，通过改变参数获取输入模式，例如改变起止点、缩小范围或改变步长，检查相同时刻/位置下的输出是否存在关系。

(3)基于数据变异设置输入模式。数据变异是对原始输入数据进行变异，蜕变关系中的输入关系也是对原始输入数据进行一种转化，两者都是针对原始输入数据进行变换，因此可以通过数据变异的方式来指导产生输入模式，本文选择7种基本的数据变异算子(表1)，为了便于检验结果，输入模式不必构造得太复杂。

表1 数据变异型输入模式

(4)组合不同的输入模式生成新的输入模式。假设根据前3种输入模式识别规则结合静态分析方法，得到了3条输入模式：xj=-xi、xj=2xi、xj=xi+1，一条输入关系的xi用另一条输入关系的xj代替，就可以组合形成新的输入模式，如xj=-(xi+1)、xj=-2(xi+1)。

本文提出的4条输入模式识别规则中，前3条规则需要结合一定的领域知识才能推导产生有意义的输入模式，第4条规则需要以已有的输入模式为基础才能组合成新的有意义的输入模式。上述规则互为补充，能够满足大多数程序推导输入关系的要求。

2.2.2 生成测试数据

蜕变测试中常用的原始测试用例生成方法是随机法和特殊值，其次采用已有的测试套件，少部分文献中使用的是工具，如约束编程、基于搜索的测试、符号执行等[1]，随机方法是一种经济有效且直截了当的方法。在选取原始测试用例时，可根据具体情况采取相应的测试用例生成策略。例如，龙格库塔法生成常微分方程程序的测试数据时，由于程序自动生成一批等差的数据，因此数据产生方式为等价类划分法。

2.2.3 输出模式

似然蜕变关系的识别在很大程度上受到测试数据的影响，分析2.2.2节产生的测试数据是否为成功的测试数据，由于输入模式是紧密结合领域知识的，且是有意义的输入关系，所以由此再来生成的测试数据，在测试输出结果数据中挖掘输出模式，显然提高了数据挖掘的针对性，有助于输出模式识别。在挖掘似然蜕变关系的输出模式时，实际上是根据预设的输出模式，利用拟合功能对输出数据进行分析。本文预设比较型输出模式和函数型输出模式，比较型输出模式包括6种形式，即小于、小于等于、等于、大于、大于等于和不等于；函数型输出模式包括10种形式，即线性、二次、复合、增长、对数、立方、S、指数分布、逆模型、幂，具体的介绍见表2。

表2 比较型和函数型输出模式

为了得到似然蜕变关系的输出模式参数和曲线的拟合效果，由于SPSS工具里面预设了多种形式的输出表达式，因此，该文利用SPSS数据分析工具进行模拟。

2.2.4 筛选似然蜕变关系

为了进一步验证所识别的输入模式、输出模式是否能够构成似然蜕变关系，需要对产生的输入模式、输出模式进行筛选，即再次生成一批测试数据，分析关系模式的有效性，值得注意的是应当尽可能地选择与原来用于生成输入模式、输出模式时不同的测试数据。如果经研究发现，输入模式、输出模式满足条件：

条件一：SPSS挖掘输出模式时的可决系数R方>0.95；

条件二：验证时的测试用例的通过率>90%。

则可视为一条似然蜕变关系；否则，则选择下一对输入模式、输出模式，直到结束。

似然蜕变关系不仅可以用来产生新的测试用例，而且可以用作验证程序运行结果的一种预判(预期输出)。因此似然蜕变关系可以用来发现程序中的错误，即观察测试用例中是否有违反似然蜕变关系的情况，如果有则认为程序中存在错误。

2.3 算法描述

根据前面的步骤，算法如下。

算法1：似然蜕变关系发现算法

/** 输入 P,Dr,n,m

输出DR,LMR

其中

P为待测程序；

Dr为静态分析程序文档导出的似然蜕变关系输入模式；

n为随机产生的测试数据序对的个数；

m为验证推导的输入模式、输出模式时生成的测试用例序对的个数；

DR为利用SPSS工具挖掘的满足可信度要求的输出模式；

LMR为验证输入模式、输出模式后，最终得到的似然蜕变关系。

算法开始 **/

//(1)对照输入关系，生成测试数据

dr_len=Dr.len(); //获取输入模式的个数

for(j=0;j

r=Dr[j];

for(i=0;i

ti=(xi, P(xi)); //随机生成程序输入，运行程序得到输出

t′i=(r(xi), P(r(xi))); //依据输入模式，生成后续测试数据

if(ti,t′i的输出结果正确)i++;

end if

end for

//(2)利用计数器和SPSS分别挖掘比较类型和函数类型的输出模式

if(P(xi)

//< ≥ ≠

If(P(xi)>P(r(xi)))gc++;ltc++; uc++;

//> ≤ ≠

if(P(xi)==P(r(xi)))ec++;//=

判断每个计算器/n是否>0.95，是则加入输出模式集Rs;

P(xi), P(r(xi))导入SPSS;

自动挖掘函数类型的输出模式集Rs;

//SPSS工具有“拟合”功能，取拟合效果R方>0.95加入Rs

DR[j]=Rs; //把Rs添加到DR中

end for

//(3)推导似然蜕变关系

for(j=0;j

r’ =Dr[j];

dR_len=DR[j].len();//取输出模式

count=0; //统计同时满足输入模式和输出模式的用例数

for(k=0;k

R’=DR[j][k];

for(i=0;i

ti=(xi,P(xi));

t’i=(r(xi),P(r(xi)));

if(ti,t’i的输出结果正确)i++; //成功的测试数据

if(R’(P(xi),P(r(xi)))count++; //计数

end if

end if

end for

end for

判断count/n是否>90%，是则将(r’,R’)添加到似然蜕变关系集LMR;

end for

3 数值例子

3.1 龙格库塔计算程序

为了展示所提出的方法的有效性，以一个常微分方程计算程序为例进行阐述。

一阶常微分方程(只求一次导)的标准形式如下

(4)

使用经典四阶龙格库塔法(Runge-Kuta)解上述表示的常微分方程，则对于该问题的求解过程如下所示

(5)

将式(4)实例化为一个常微分方程

(6)

3.2 实现过程

3.2.1 提取输入模式

选定四阶龙格库塔法求解常微分方程计算程序后，首先输入模式的识别，以下即为对应2.2.1节中提到由静态分析导出的4类输入模式。

(1)数值解的性质

r-1.1：分析其算法的数值解的数学性质，其数值解具有单调性，取输入模式xi

(2)输入数据的数值特性

r-2.1：龙格库塔法算法的调用方式为RK4(起始坐标, 起始点的结果, 终止坐标, 数据个数, 常微分方程)，改变起始坐标点，其它参数保持不变。

r-2.2：设置不同的步长，除了数据个数外，其它参数保持不变。

r-2.3：交换运算，交换起始坐标和终止坐标，将第一次运行得到的终止坐标的输出结果作为预置参数。

(3)数据变异关系

r-3.1：对原始用例取负数，x’=-x。

r-3.2：对原始用例取倍数，x’=2x。

r-3.3：对原始用例自增1，x’=x+1。

(4)组合输入模式

r-4.1：组合r-3和r-4.1，得到x’=-2x。

r-4.2：组合r-4.1和r-4.2，得到x’=2*(x+1)。

3.2.2 生成测试数据

常微分方程程序的调用格式是RK4(x0,y0,x,n,pfunc)，由于程序本身的性质，将x0到x等份切割为n+1个数据，得到的测试数据格式为(xi,yi)，将xi看作有意义的输入数据，yi看作输出数据，因此本文采用的数据生成方式为等分等价类。针对每一条输入模式生成100组测试数据，以r-3.2输入模式为例进行说明，本文产生所有数据见GitHub：https://github.com/CsAndIt/LMR2020。

r-3.2输入模式为2倍倍数关系，首先生成原始测试数据，调用RK4(1,1,2,100,pfunc)生成从1到2总共100个数据，然后由输入模式获取输入对应为2倍的数据，即生成2到4的数据，调用RK4(1,1,4,300,pfunc)生成，选取后续测试数据中对应原始测试数据为2倍的数据，表3展示了部分数据。

表3 两倍输入模式生成的测试数据

3.2.3 挖掘输出模式

生成数据后，针对 数据组，挖掘蕴含的输出模式，根据预设的6种比较模式和11种函数模式，比较模式输出关系用不同的计数表示。以第6条输入模式为例，满足条件的比较类型的输出模式有：<、≤和≠；得到的函数模型汇总情况见表4，曲线拟合图像如图4所示。

表4 模型汇总和参数估计

图4 曲线拟合效果

取R方大于等于0.95的拟合曲线为输出模式，得到二次、三次和幂形式的函数关系，根据表2的函数关系式填入参数后，由于三次和幂关系与二次关系重合了，只取其中一个即可，得到了输出模式y’=0.05y2。

用同样的方法，分别执行其它输出数据对，每条输入模式与对应数据挖掘得到的输出模式见表5。

3.2.4 验证似然蜕变关系

由表5得到了33组输入模式、输出模式，输出模式为比较类型的模式对无需再验证，这是因为在大概率上与推导的模式对是一致的。下面将针对M7、M8、M12、M14、M18、M22、M26、M30这8条模式对生成测试数据，每组关系模式生成80对数据，来验证输入模式、输出模式的正确性，由于程序在计算时出现了截断误差，综合考虑后，采取通过率在90%及以上的作为一条成功推导的似然蜕变关系，测试数据通过率如图5所示，实验结果分析发现，本文的方法可以有效地发现常微分方程程序的似然蜕变关系。

表5 输入、输出模式汇总

图5 输入、输出模式验证的通过率

3.3 实验结果分析

在3.2节中介绍了似然蜕变关系的识别方法，但是还需对结果进行验证，本文采取的方式是与函数解析式及程序性质进行对比，筛选出符合程序属性和要求的似然蜕变关系，解释说明见表6。

表6 似然蜕变关系的筛选

常微分方程式(6)的解析式为

y=e3*e-3x(7)

由于M7和M12分别与M4和M9重复，因此剔除，剩下的31种模式对都可看作程序的似然蜕变关系。比较类型的似然蜕变关系有25条，占比80.65%；函数类型的似然蜕变关系，由于在导出输入模式时没有穷尽所有的可能性，根据每种规则分别只实例化一条输入模式，故而生成得少。根据实验结果得知，实验较好地识别出了龙格库塔计算程序的似然蜕变关系。

通过与Zhang等[8]提出的一种自动发现和清理数值蜕变关系的识别方法相比，由于本文结合领域知识推导有意义的输入模式，避免了输入形式预设的盲目性，而且输出模式也囊括了更多的关系类型，包括比较关系及多种函数关系。进一步可知，依据有意义的输入模式来生成测试的输入数据，相应得到的输出数据，在一定程度上提高了数据挖掘的针对性，也将为后续的输出关系的挖掘降低冗余做准备。

4 结束语

本文从程序算法层面数学性质方面分析中，得到了识别输入模式的4条规则，可以支持对输入模式的识别和测试数据的生成；利用SPSS工具对依据输入模式产生的程序运行结果进行挖掘，得到了近似真正的输出模式；通过对龙格库塔算法程序的研究分析发现，本文提出的似然蜕变关系识别方法在实际应用中是可行的、有效的。由于输入模式是针对常微分数值程序而言的，下一步工作就如何建立更加有效的输入模式识别规则以及推广该方法的实际应用进行研究。