联合不相关回归和非负谱分析的无监督特征选择

朱星宇，陈秀宏

（1.江南大学 人工智能与计算机学院，江苏 无锡 214122;2.江南大学 江苏省媒体设计与软件技术重点实验室，江苏 无锡 214122）

在信息时代背景下产生了海量的高维数据，然而这些数据通常含有大量冗余特征和噪声，降低了算法的性能。因此，如何从高维数据中选出最有效的特征即特征选择已成为一项研究热点，特征选择旨在通过去除冗余、不相关和有噪声的特征，找到一组简洁且具有良好泛化能力的特征，由此产生的方法已在机器学习[1]、数据挖掘[2]和生物信息学[3]等领域得到了广泛的应用。基于是否使用标签，特征选择方法可分为有监督学习[4]和无监督学习[5]。

有监督学习依赖于数据的标签信息，并利用它直接指导学习过程。然而，从未标记数据中提取最有判别性的信息是一个具有挑战性的问题，由于无监督特征选择可以根据原始数据的潜在属性来确定特征的重要性，因此近年来越来越受到研究人员的关注。本文主要研究无监督特征选择方法。

基于谱分析的无监督特征选择因其出色的性能引起了广泛关注，本节将回顾一些比较经典的谱特征选择方法。无监督的判别特征选择(L2,1-norm regularized discriminative feature selection for unsupervised learning)[6]联合使用判别分析和L2,1范数进行无监督特征选择，它虽然可以选择判别性的特征，但却忽略了数据间的内在结构。Nie 等[7]提出了灵活流形嵌入(flexible manifold embedding:a framework for semi-supervised and unsupervised dimension reduction)作为降维的一般框架，非负判别特征选择(unsupervised feature selection using nonnegative spectral analysis)[8]则在FME 框架中结合特征选择和谱聚类学习，它具有鲁棒非负矩阵分解、局部学习和鲁棒特征学习的优势。联合嵌入学习和稀疏回归(joint embedding learning and sparse regression:a framework for unsupervised feature selection)[9]是基于FME 和L2,1范数的特征选择方法，它致力于嵌入学习高维样本的低维表示。最近，Nie 等[10]提出了结构最优图特征选择(unsupervised feature selection with structured graph optimization)，该方法同时执行特征选择和局部结构学习，同时它可以自适应地确定数据间的相似性矩阵，但过于严格的正交约束选择出的特征会丢失一定程度的判别性，从而降低他们在聚类或分类任务中的性能。自适应图的广义不相关回归(generalized uncorrelated regression with adaptive graph for unsupervised feature selection)[11]通过最大熵来自适应地构造相似图，进而同时进行特征选择和谱聚类，但它在学习相似图时采用标签矩阵学习，没有考虑原始数据的类簇结构，这显然不是很合理。

尽管上述无监督特征选择方法已经在各种应用中取得了良好的性能，但仍有以下不足：1)上述基于谱特征选择的方法构造的相似图是从原始数据得到且是静态的，而现实世界的数据始终包含大量噪声，这使得静态相似矩阵很不可靠，进而破坏局部流形结构；2)最优相似矩阵应具有精确的c个连通分量（c是类簇数），它能更准确地揭示数据的局部邻域结构；3)通过传统正交约束选择出的特征虽达到了低冗余的目的，但会丢失一些判别性的特征，这些特征在分类任务中往往能起到关键作用。

综合上述分析，本文联合广义不相关回归、结构化最优图和非负谱分析，提出一个联合不相关回归和非负谱分析的无监督特征选择模型。模型中对相似矩阵增加包含精确的c个连通分量的约束，可以用来动态学习结构化最优图，进而更准确地揭示数据之间的局部结构信息；同时通过非负谱聚类可以学习到更真实准确的聚类指标；利用广义不相关约束的正则回归方法选择不相关和判别性的特征，有效避免不相关约束导致的平凡解。在不同数据集上的实验表明所提出的方法是有效的，且该模型在无监督二维图像的特征选择领域，如：医学图像分类、人脸识别、模式识别等计算机视觉任务方面有着广泛的应用价值。

1 相关工作

1.1 广义不相关回归模型

无监督特征选择也可以表示为回归模型，从而正则化回归模型也广泛应用在无监督特征选择中。但是，已有工作忽略了特征的不相关性。尤其是当只需少量特征时，需要选择最具判别性的特征。Li 等[11]提出的以下广义不相关回归模型(generalized uncorrelated regression model，GURM) 可以获得具有判别性且不相关的流形结构：

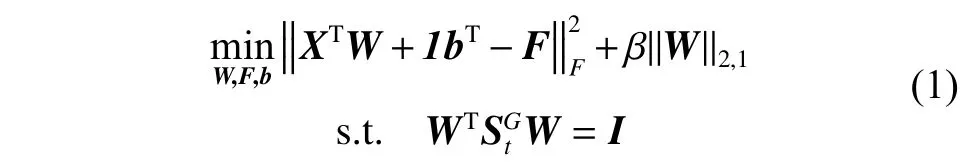
式中：W∈Rd×c是回归矩阵，b∈Rc×1是偏差项，F∈Rn×c是学习的嵌入聚类结构；正则化项‖W‖2,1可使得W的行是稀疏的，进而选择重要的特征；β是正则化参数，β越大，W行越稀疏；=St+βG为广义散度矩阵，G为d×d对角矩阵，其对角元素定义为

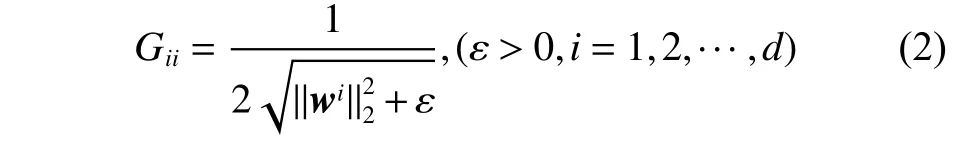
这里，ε>0是一个很小的值，可避免因W的行稀疏而导致的分母为0 的情形；St=XHXT是样本数据的总散度矩阵。一般地，当样本数量小于数据维度时，St是奇异的，而SG t总是正定的，这样约束条件可使数据在投影子空间中是统计不相关的，这样可以很好地保留数据的全局结构。当 β很小时，可使投影后样本之间高度不相关，因此，约束条件在描述样本的不相关性时要优于正交约束WTW=I和传统不相关约束WTStW=I。

1.2 局部结构学习

研究表明，相似性矩阵可用来描述数据间的局部结构。然而，大多数构造相似性矩阵的方法并没有考虑原始数据中的冗余特征和噪声，从而导致所学习到的局部结构不够准确，最终影响特征选择的结果。本节采用一种自适应确定相似度矩阵的方法[12]，可以同时执行特征选择和局部结构学习。

两个数据样本相邻的概率可以用来描述它们之间的相似度，记相似度矩阵为S∈Rn×n，其中元素sij表示相似性图中与样本xi和xj相对应的结点之间相连的概率。样本xi和xj越接近，则对应的连接概率sij越大，它与对应结点之间的距离成反比。相似度矩阵S∈Rn×n可通过以下优化问题得到：

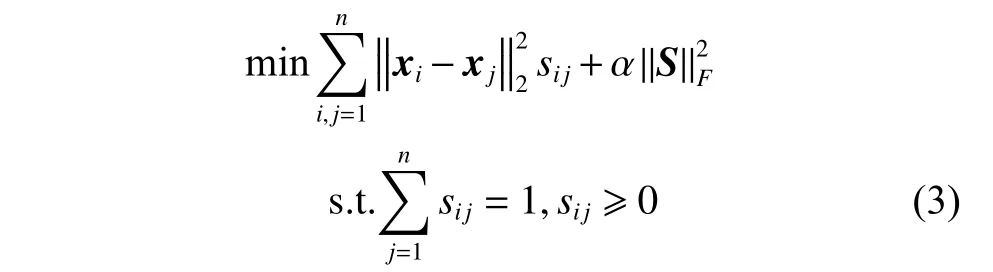
1.3 结构化最优图学习

如果学习得到的相似矩阵恰好包含c个连通分量时（即它仅含有c个对角分块），则每个样本的近邻是最佳的。但是，问题(3)(式(3))的解一般不具备此性质，大多数情况下其解只包含1个连通分量[12]。

受文献[14]的启发，对拉普拉斯矩阵LS=DS−的秩进行约束可使得矩阵S具有c个连通分量。这时，问题(3)转化为

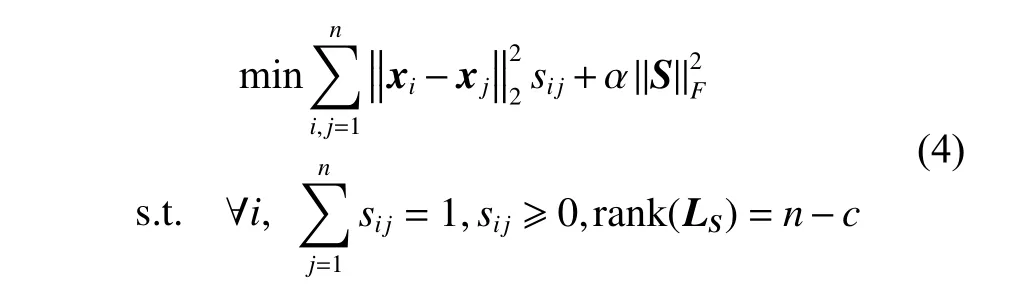
然而，问题(4)(式(4))很难直接求解，因为秩约束是一个复杂的非线性约束。假设半正定矩阵LS的n个非负特征值依次由小到大排列σ1(LS)≤σ2(LS)≤···≤σn(LS)，则问题(4)可转化为

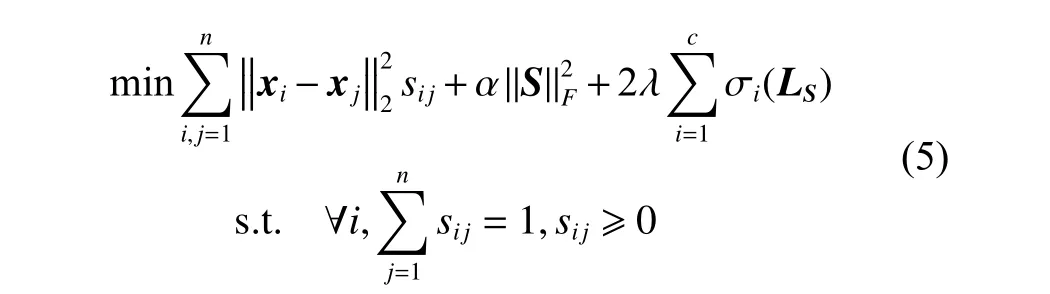
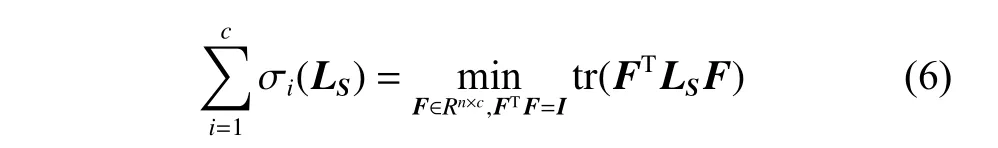
这里F∈Rn×c是类指标矩阵。故问题(5)(式(5))可重写为

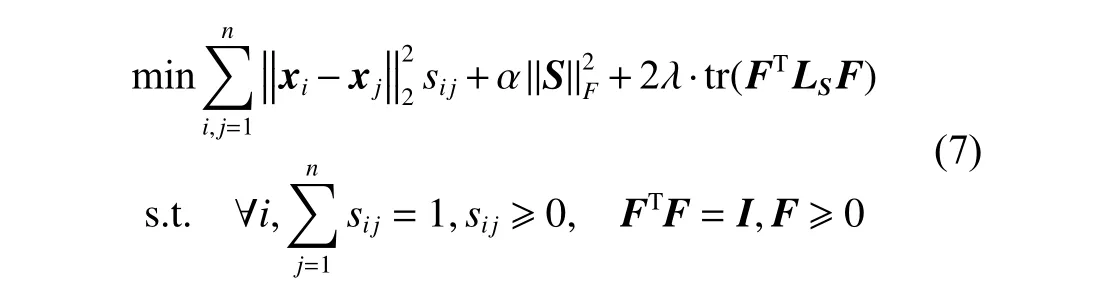
正交非负约束可使得F的每一行只有一个元素大于0，其他元素都等于0。从而得到的类指标矩阵F更准确，且获得更具判别性的信息。此外，求解问题(7)(式(7))得到的S包含精确的c个连通分量，能够捕获更准确的局部结构信息。

2 联合不相关回归和非负谱分析模型(JURNFS)

2.1 模型建立

根据流形学习的理论，希望原始空间中样本的近邻关系在低维投影空间中得到保持，为此，本文讨论在低维空间内学习最优图。设W∈Rd×c是投影矩阵，则由(7)可得到以下模型：

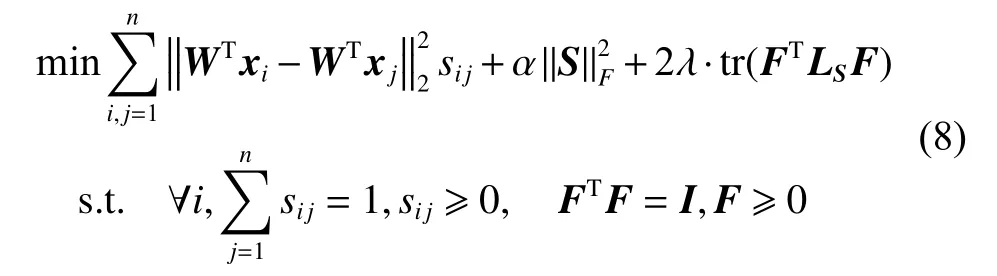
将模型(8)(式(8))与稀疏回归模型(1)相结合，得到本文联合不相关回归和非负谱分析模型：

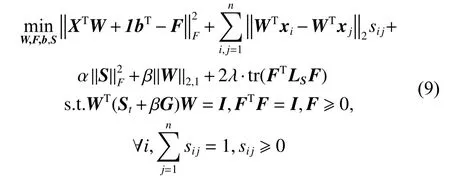
其中，α、β、λ是正则化参数。在式(9) 中,第1 项、第4 项和第5 项刻画了无监督不相关回归和非负谱分析，用于学习稀疏投影矩阵和预测标签矩阵，且L2,1范数可使得W保持行稀疏，从而能够选择出更具有价值和判别性的特征；第2 项和第3 项用于学习数据的局部结构，确保原始空间内数据的相似结构在投影子空间内得到保持。这里第2 项未采用L2范数距离的平方，这是考虑到若原始数据中有噪声，平方会扩大噪声对模型学习与分类的影响。

令问题(9)(式(9))关于b的 拉格朗日函数为

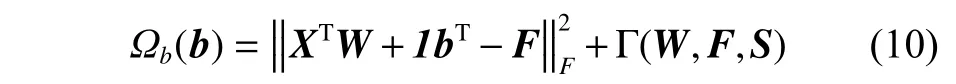
其中，Γ(W,F,S)表示式(9)中依赖于W、F、S但又独立于b的项。取Ωb(b)关于b的导数并令其等于0，得

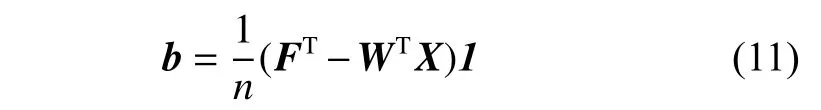
在实际应用中，数据结构总是多模态的，为了在多模态数据上获得更好的性能，可以研究图的局部性。假设S的每一行有一个具体的αi[13]，再结合式(11)，问题(9)可重写为

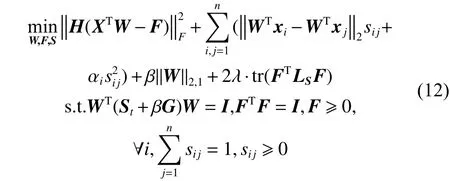
此时，参数 αi可以控制每个样本自适应近邻的数量[12]。

2.2 模型求解

由于式(12)中的目标函数是凸的，故它有全局最优解，但直接求其全局解比较困难。本节给出一种交替优化方法来迭代求解它。

1)固定F和S，更新W

此时，问题(12)(式(12))等价于以下问题：

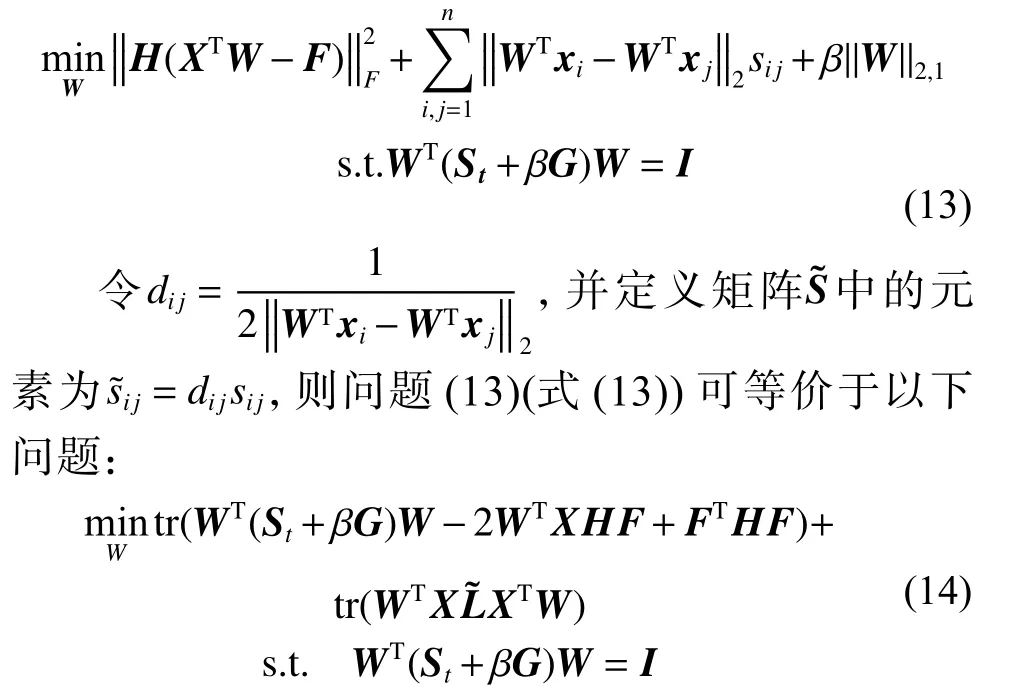
该问题将不相关性表现为流形结构，且具有闭式解。问题(15)(式(15))可表示为

问题(16)(式(16))可以利用广义幂迭代方法[16]求解，详细过程见算法1。

算法1求解问题(14)

此时，问题(12)等价于：

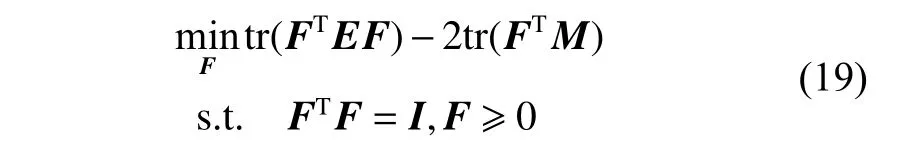
其中，E=H+2λLS，M=HXTW。

此问题可采用乘性更新规则[17]来求解。首先考虑它的松驰问题：

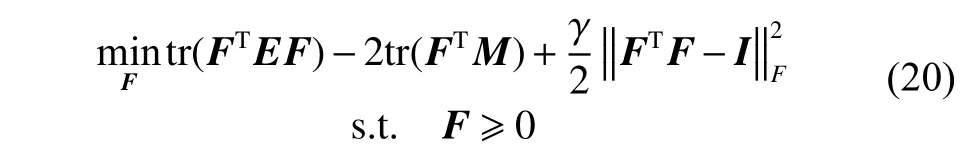
其中，γ为充分大的正数，由KKT 最优性条件得

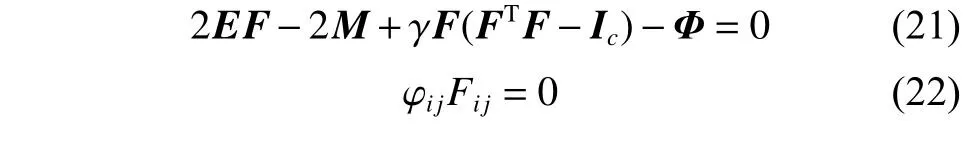
这里，φij为对应于约束Fij≥0的非负拉格朗日乘子。于是有以下更新规则：

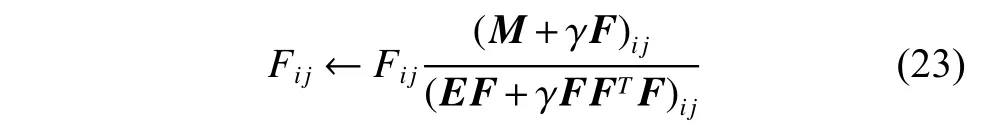
再对F的每一列归一化使得它满足条件(FTF)ii=1,i=1,2,···,n。

3)固定W和F，更新S

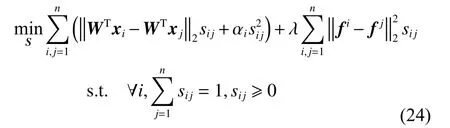
其中，fi和fj分别为F的第i行和第j行。该问题可分解为以下n个独立的子问题：

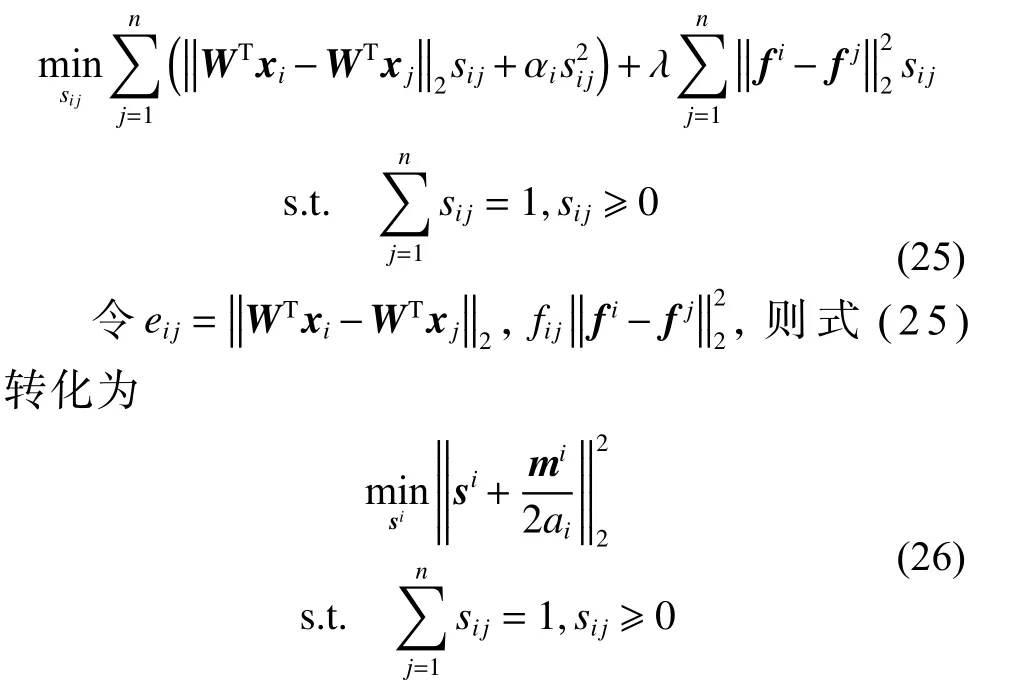
其中，mi=(eil+λfil,···,ein+λfin)。

该问题可利用文献[18]中的方法求解，并可自适应地确定式(9)中参数α[13]，进而获得具有精确k个非零分量的最优解si。

以上3 步可迭代地进行，直到目标函数收敛或满足终止条件，整个过程概括为算法2。

算法2JURNFS

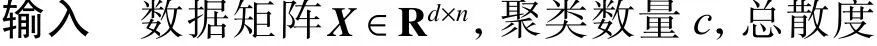
2.3 时间复杂度分析

在以上算法中，主要的计算复杂度为步骤①中的奇异值分解和矩阵求逆，故本算法时间复杂度最高为O(n2d)，假设算法迭代T次，则该部分的时间复杂度为O(Tn2d)，从而整个算法的时间复杂度为O(Tn2d)。

3 实验及分析

3.1 实验方案

在本节中，通过进行大量实验以充分验证本文所提出方法的有效性和优越性。在展示结果之前，首先提供一些详细的实验方案。

1)数据集：实验中使用了6个公共数据集，包括2个人脸数据集ORL[19]和BIO[20]，1个物体数据集COIL20[21]，1个手写字数据集BA[22]，1个树叶数据集LEAVES[23]以及1个生物学数据集LUNG[24]。数据集的详细信息见表1 及图1 所示。

图1 部分数据集的图片Fig.1 Visualization of some datasets

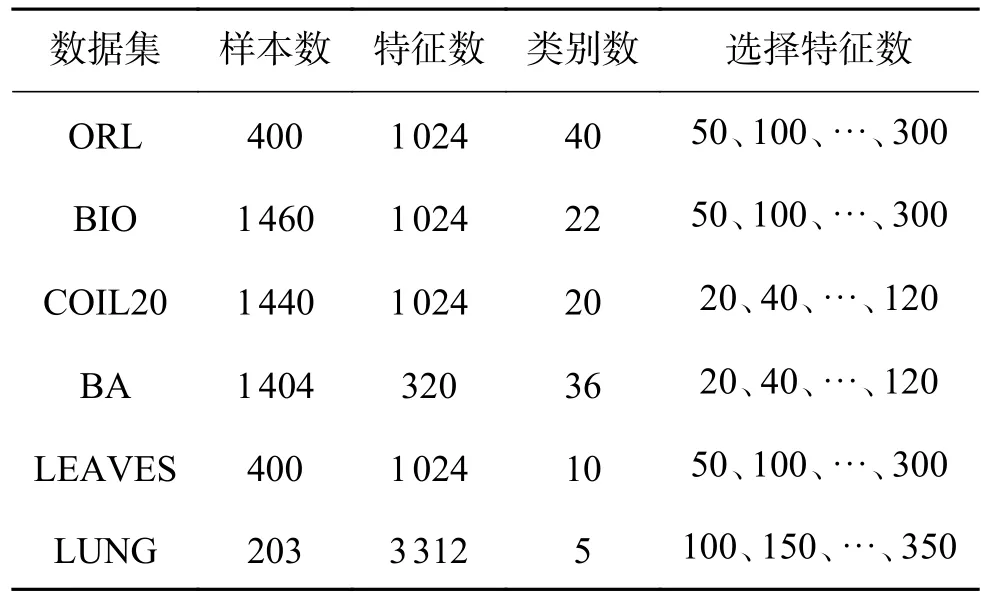
表1 数据集信息Table1 Detail introduction to datasets

2)对比算法：实验中将本文所提出的联合不相关回归和非负谱分析模型(joint uncorrelated regression and nonnegative spectral analysis for unsupervised feature selection,JURNFS)与5个特征选择方法进行了比较，分别是：无监督判别特征选择(L2,1-norm regularized discriminative feature selection for unsupervised learning,UDFS)[6]、非负判别性特征选择(unsupervised feature selection using nonnegative spectral analysis,NDFS)[8]、联合嵌入学习和稀疏回归(joint embedding learning and sparse regression:A framework for unsupervised feature selection,JELSR)[9]、最优结构图的特征选择(unsupervised feature selection with structured graph optimization,SOGFS)[10]和用于无监督特征选择的自适应图的广义不相关回归(generalized uncorrelated regression with adaptive graph for unsupervised feature selection,URAFS)[11]。

3)评价指标：为了验证所选特征的优劣性，本文利用两个度量标准来衡量每种算法的性能，一个是识别精度(ACC)[25]，定义：

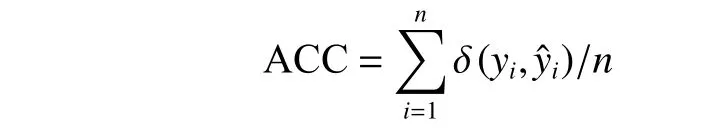
式中：yi是每一个样本的真实标签；是对应的预测标签；n是测试样本的数量；函数δ(·,·)衡量两个输入参数之间的关系，如果两个参数相等则等于1，否则等于0，聚类精度越高，说明算法的效果越好；另一个评价指标是标准化互信(NMI)[26]，定义：

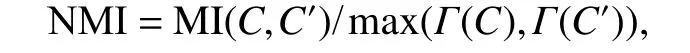
式中：C是真实标签的集合；C′是预测标签的集合；MI(C,C′)是互信息指标；Γ(C)、Γ(C′)分别是C和C′的熵。NMI 越大，表示算法性能越稳定。

4)参数设置：本文通过网格搜索来确定每个算法的最优参数，所有算法的参数都是从{10−4,10−3,10−2,···,102,103,104}中选取。此外，在聚类实验中，本文采用流行的K-means 聚类方法，用于对具有选定特征形成的新数据进行聚类，每个数据集的选择特征数在表1 中列出。为减少Kmeans 中随机起点触发的偶然性影响，对每种算法进行10 次聚类，并计算平均值。对于分类实验，本文使用1-最近邻(1-NN)分类器对选定特征的测试图像数据进行分类。为了减少偏差，所有实验均重复运行10 次以随机选择训练样本，最后计算平均分类结果。另外，K-means 聚类方法中的K值设置为c，并且将每种方法中子空间的维数也都设置为c，除SOGFS 的子空间维数设置为d/2。在UDFS、NDFS、JELSR、SOGFS 和JURNFS 中，最近邻k的数量设置为5。

3.2 聚类性能与分析

本节将不同方法的聚类精度进行比较，实验中将每个数据集的所有样本都用作训练集。首先，每个算法在每个数据集上进行学习以选择重要且具有判别性的特征，不同数据集所选特征数也不一样，具体细节见表1；然后，本文使用K-means聚类算法对由这些选择出的特征所形成的新样本进行聚类实验。图2 给出了6个算法在6个数据集上的聚类精度，从图2 可以看出，在大多数情况下，本文所提出的JURNFS 相比其他算法都取得了比较好的效果，这证明了JURNFS 的优越性。

此外，1)从图2(a)和(b)可知，JURNFS 在人脸数据集上的效果远远领先于其他5个算法，并且JURNFS 在ORL 和BIO 上相对于其他算法分别平均提升了约3.28%和4.75%，这是因为JURNFS 通过学习数据的局部流形结构选择出了人脸上更具有判别性的特征，这些特征能够显著地代表原数据，因而获得了较高的聚类精度。2)所有算法在COIL20 和BA 数据集上的聚类效果都比较接近，这可能是由于这两个数据集里的样本特征区分度信息不是很高，所有算法学习到了近似的局部结构，而JURNFS 中采用的广义不相关约束在保留低冗余度特征的同时维持了对判别性部分特征的关注（如COIL20 中物体的轮廓商标部分；BA 中文字笔画拐弯部分），所以JURNFS 的聚类效果仍能够优于其他算法。3)在LEAVES和LUNG 数据集上，所有算法的聚类效果随着所选特征数而波动。这也证明并不是选择的特征数越多，聚类效果越好。因为特征越多，冗余的特征也可能越多，因此有必要进行特征选择。而JURNFS 采用低维流形结构化最优图学习和广义不相关回归联合学习的方式保留了判别性局部结构信息（如LEAVES 中叶的根茎部，LUNG 中的病灶部分），因此在处理非人脸数据集时仍能具有较好的性能。此外，可以发现LUNG 数据集的数据量较大，标签类数只有5，因此每一类标签的训练数据集较大，这也可能是JURNFS 优于其他算法的原因，因为在这种情况下JURNFS 可以选择更准确、更判别性的特征。总之，通过特征选择获得的精炼的数据包含更多有价值的信息，而JURNFS 通过广义不相关回归以及结构化最优图，所选择的特征更具判别性及有效性，因而可以获得更好的性能。

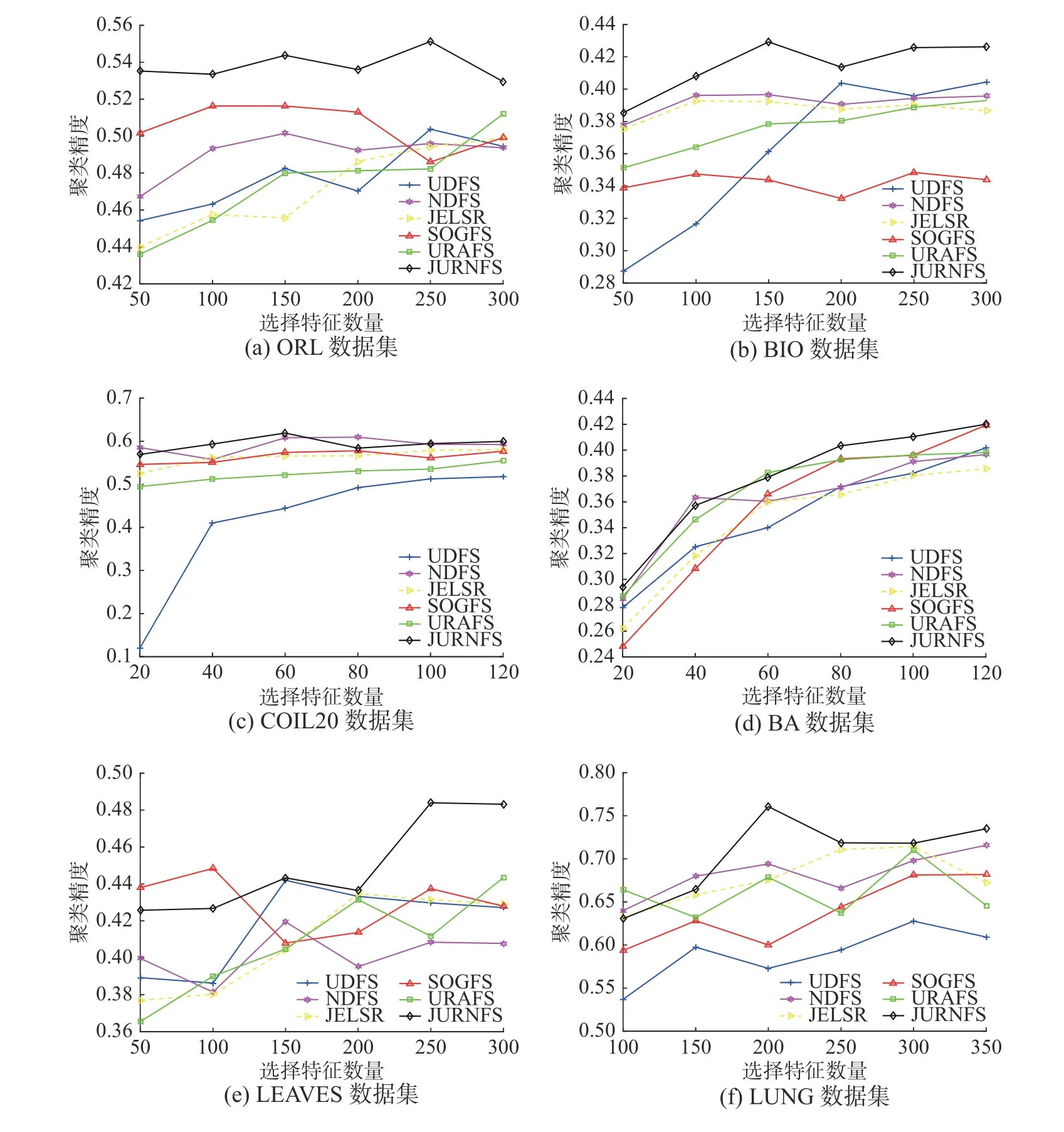
图2 6个算法在6个数据集上的聚类精度Fig.2 Clustering accuracies of six methods on six different datasets

为了进一步说明JURNFS 的优越性，表2 给出了在6个不同的数据集上6 种不同算法的标准偏差的最优NMI 值，其中最优值以黑体加粗。一般而言，NMI 值越高，特征选择的性能越好。显然，与其他特征选择算法相比，JURNFS 的NMI 相对较高，这也表明JURNFS 具有更好的算法性能。

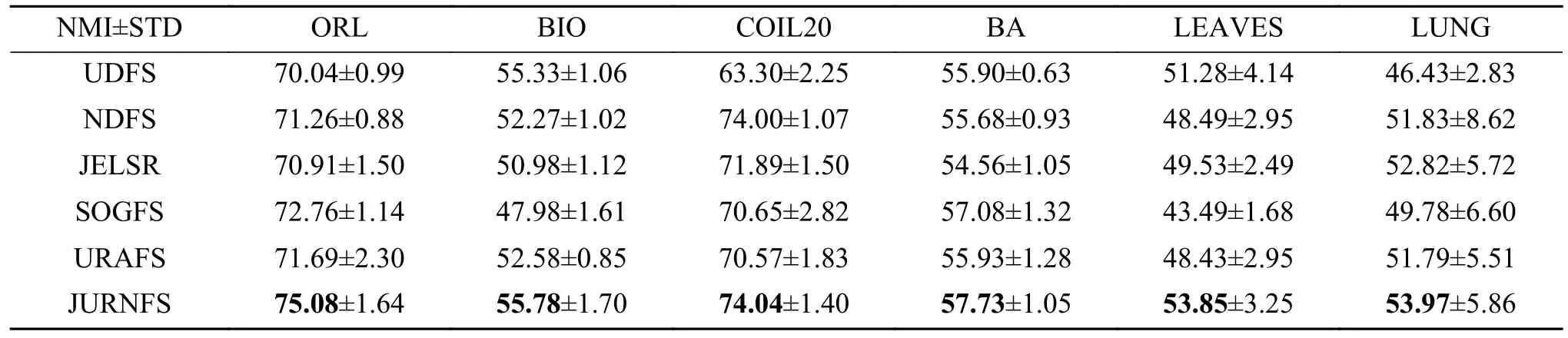
表2 不同数据集上不同方法的最佳NMI (标准偏差)Table2 Best NMI with standard deviation of different methods on different data sets %

3.3 分类性能与分析

本节将不同方法的分类精度进行比较，首先从不同数据集上的每个类中随机选取适当数量的样本作为训练样本，其余的作为测试样本。对于ORL、LEAVES 和LUNG 数据集，随机选取5个图像样本作为每类的训练样本，剩余的作为测试样本。对于BIO、BA 和COIL20 数据集，随机选取10个图像样本作为每个类的训练样本，剩余的作为测试样本。此外，不同的数据集在实验中选取的特征数量也不同(见表1)。

图3 描述了不同特征选择方法的分类精度随所选特征数量的增加而变化的情况。由该图可以发现JURNFS 在所有数据集上都能取得很好的分类效果，这得益于JURNFS 联合使用广义不相关回归和非负谱分析，在保留全局结构的同时自适应进行局部结构学习，很好地保留了特征的判别性信息，这些判别性特征在后续进行分类任务时起到了关键作用。

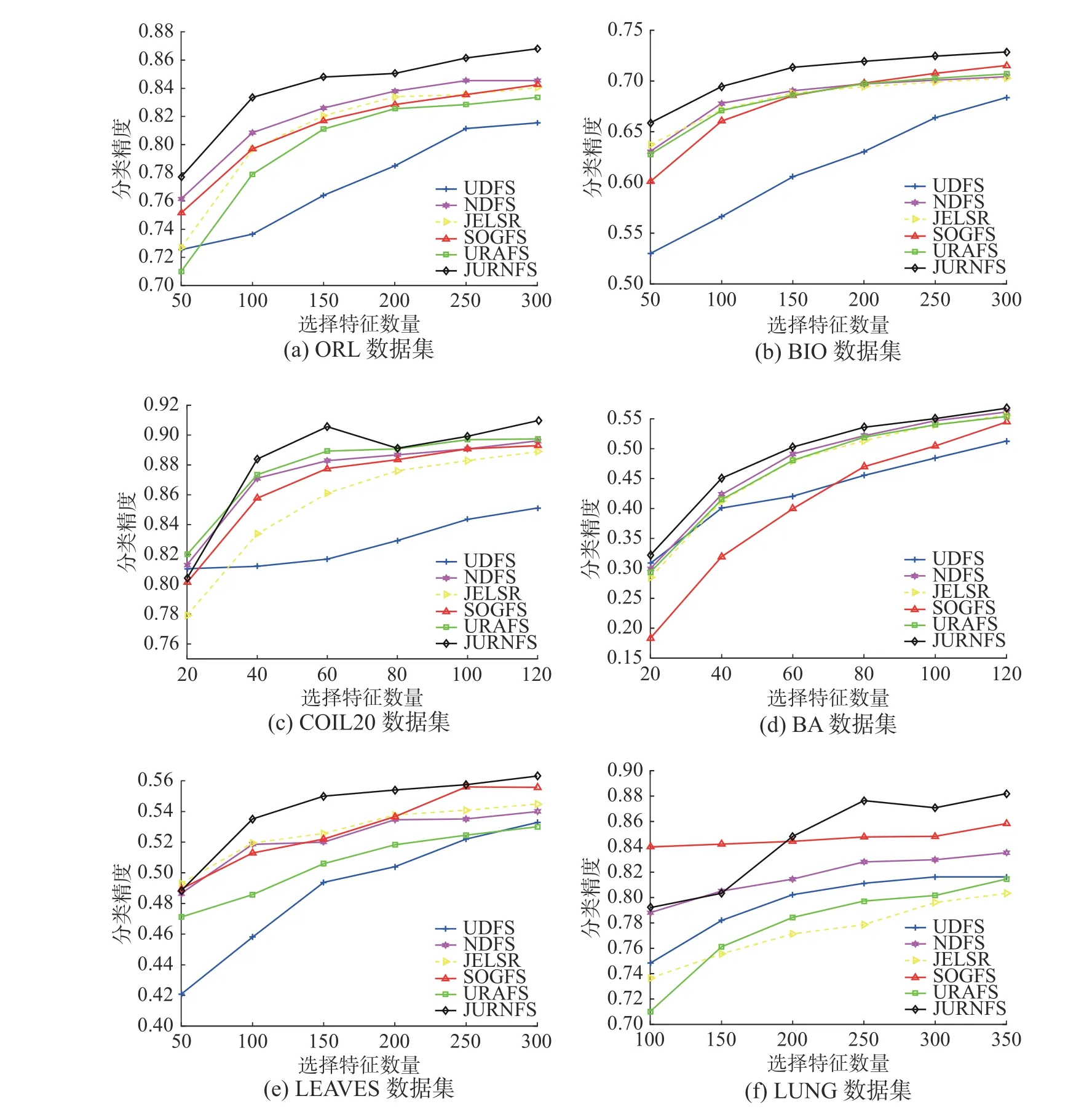
图3 6个算法在6个数据集上的分类精度Fig.3 Classification accuracies of six methods on six different datasets

此外，图4 通过重构图展示了部分算法在ORL 数据集上选择的特征，不难看出：1)随着选择特征数的变化，JURNFS 可以选择信息量较大的特征（如眼睛、鼻子、嘴巴），并且JURNFS 在选择特征数较少的情况下会优先选择具有判别性的特征；2)对于SOGFS，尽管它在聚类任务中表现良好，但它选择的特征主要分布在皮肤区域，而不是人脸的区分器官特征。这表明边缘和轮廓上的特征有助于提高这些方法的聚类性能。

图4 6个算法在ORL 数据集上的重构图，所选特征个数从左到右依次为{150,250,350,450,550,650,1 024}Fig.4 Reconstruction graph of 6 algorithms on ORL data set,the number of selected features from left to right is {150,250,350,450,550,650,1 024}

3.4 算法参数与性能分析

本节将分析JURNFS 中参数的稳定性。在所提出的模型(9)中，有3个参数：α、β、λ。其中，正则化参数α用于保证在学习相似矩阵S时，每个样本都有机会成为xi的近邻；正则化参数β用于调整投影矩阵W的稀疏性；正则化参数λ确保学习到的样本标签足够平滑。因此，参数α、β、λ共同调节回归与特征选择之间的效果。在实验中，可以根据文献[15]中的方法自适应确定参数α，因此，本节将专注于研究参数β和λ对模型的影响。这里只给出JURNFS 在数据集ORL、BIO 和COIL20 上的不同参数组合变化图。

观察图5 可知，在ORL 和BIO 数据集上，JURNFS 受λ的影响较小，而随着β的增大，JURNFS的聚类效果显著提高。这可能是由于在人脸数据集上，JURNFS 经过有限次迭代学习到的标签矩阵接近于真实标签，故λ对目标函数的影响不大，而随着β增大，使得W更加稀疏，因而选择出的特征更加具有判别性及代表性，故聚类效果得到提升。在COIL20 数据集上，JURNFS 的聚类效果随着β和λ的变化而波动，这表明此时β和λ同时影响着JURNFS 的聚类效果，并且随着β的增大，JURNFS 的聚类精度会呈现出一个先增加后减少的趋势。因此在实验中，对于不同数据集仍需要找到一组合适的参数。

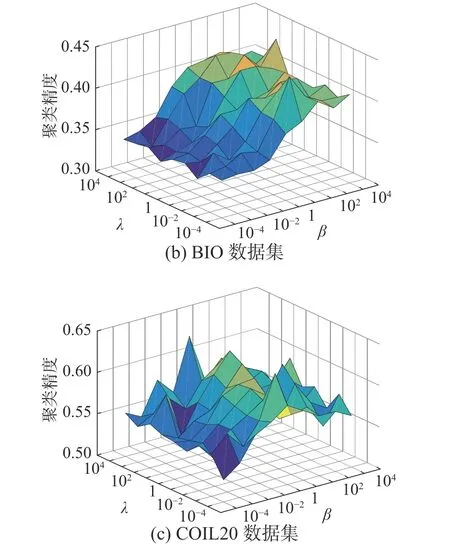
图5 JURNFS 在不同数据集上不同参数组合的聚类精度Fig.5 Clustering accuracies of JURNFS with different parameter combinations on different dataset,respectively

为验证JURNFS 算法的收敛性，本文考虑在数据集ORL 和BA 上验证式(9)中目标函数随迭代次数增加的变化情况。从图6 可见，随着迭代次数增加，目标函数值单调减少，且在5 次迭代后即可收敛，这也验证了JURNFS 的高效性。

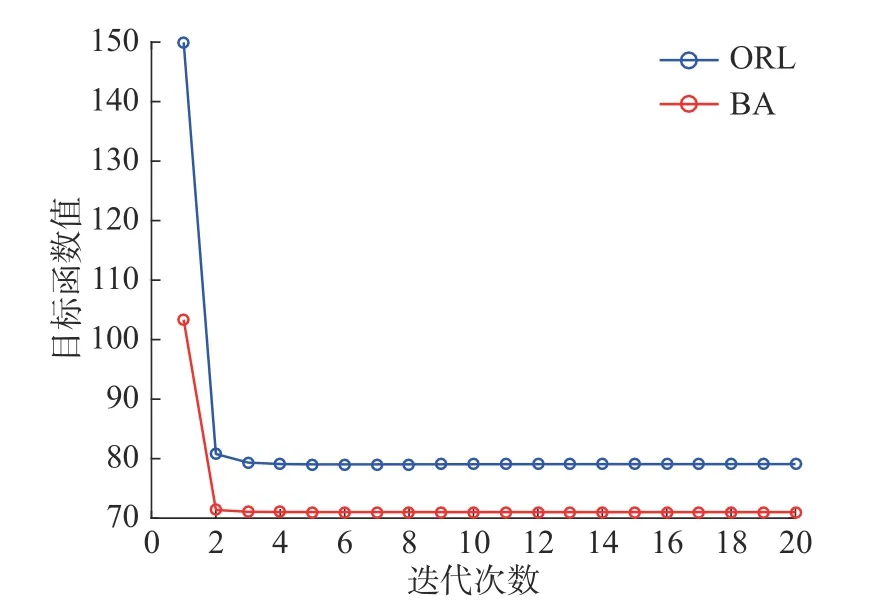
图6 JURNFS 在不同数据集上的收敛性Fig.6 Convergence behaviors of JURNFS on different datasets

此外，本文还通过算法的运行时间来评估JURNFS 的性能。本文将所有算法在ORL、BIO、COIL20 和BA 数据集上的聚类时间进行比较。不同算法的运行时间见表3。可以看到，JURNFS 的运行时间与其他算法相比仍具有很好的竞争力。

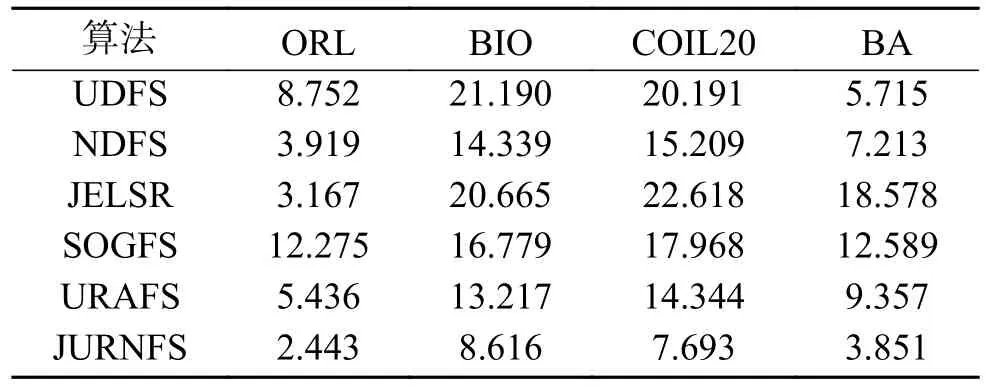
表3 不同方法的运行时间Table3 Computational time of different methods s

4 结束语

本文提出了一种新颖的无监督特征选择方法，将广义不相关回归、结构化最优图和非负谱分析结合，通过广义不相关回归模型选择不相关和判别性的特征，利用结构化最优图自适应学习数据间的局部结构信息，同时结合非负谱聚类来学习局部流形中的标签矩阵，这使得所学习到的标签矩阵更真实可靠。文中还提出了一个有效的迭代算法来求解提出的模型，并在真实数据集上进行了大量实验证明了该方法的有效性和优越性。后续的工作主要集中在以下2个方面： 1)提高算法在不同噪声（如光照、遮挡等）水平下的鲁棒性；2)提高算法处理高维数据的速度。