初中优秀数学教师教学行为特征的个案研究

傅海伦 张晓芸

摘  要：教学行为是教师在课堂上的外在活动表现，是课堂和教学论结合的途径，已成为研究数学教师课堂教学的重要角度. 研究采用质性和量化相结合的方式，利用文献资料和录像分析，对优秀教师的“因式分解”一课中的数学教学行为进行了整体和各环节的分析. 结果表明该教师在整体教学过程中呈现出明显的教学行为特征，各教学环节之间的教学行为存在着明显差别，并在此基础上提出了改进数学教师教学行为的建议.

关键词：教学行为;数学课堂;因式分解;个案研究

一、问题的提出

教师作为数学课堂的设计开发者和主导者，其教学行为对课堂教学质量的提高和学生数学素养的发展具有重要作用，教师行为研究将会在一定程度上改变课程与教学论的现有学科生态群落. 对优秀数学教师的课堂教学行为进行质性和量化相结合的分析，既可以规避质性分析因依赖研究者的经验所产生的不可靠性，又避免了量化分析依赖于数据关系的局限性. 一方面，通过归纳优秀数学教师的教学行为的流程和阶段特征以便获得整体性的结论;另一方面，通过量化该教师具体的教学行为以便获得行为变化的客观规律. 两者相互结合，互为补充，扬长避短，提高了研究的可靠性、科学性和完整性. 由此得出的研究结果将有利于教师进行经验总结和反思，可为教师教学能力的提高和数学教学思想的升华提供实践案例，为数学课堂的教学评价提供数据支撑.

本研究通过将该优秀数学教师的课堂实录转换为文本信息，并对搜集的数据进行归纳整理，旨在研究如下问题：（1）从整个教学过程来看，授课教师的数学教学行为有什么特征？（2）在教学的四个环节中，授课教师教学行为的出现有何明显差异？（3）授课教师教学行为有何不足？该如何改进？

二、研究方法

1. 核心概念的界定

行为即受思想支配而表现出来的外在活动. 我们通常认为广义的教学行为是指教师的教和学生的学;狭义的教学行为是指教师在教学中所表现出来的行为活动. 国内的教师教学行为研究可追溯到20世纪50年代，而国外的克雷茨（Kratz）更是在19世纪90年代就为教师教学行为的分类研究奠定了基础. 裴娣娜指出教学行为就是在课堂上表现出来的行为，并根据教学行为的指向性，在2007年将教学行为分为陈述行为、指导行为、展示行为、提问行为、反馈行为、管理行为、观察行为、倾听行为、反思行为、评价行为. 在各类教学行为的研究中主要采用的方法有课堂观察法、课堂语言行为互动分析法和人种志方法.

2. 研究对象

本研究选取了中国教育学会中学数学教学专业委员会第十一届初中青年数学教师优秀课展示与培训活动中的现场直播课，本次授课教师为来自厦门的陈老师，授课内容为“因式分解”，授课时长为50分钟.

3. 研究方法和过程

本研究主要采用文献分析法和录像分析法，对陈老师的数学课进行整体和分环节的质性描述和量化研究. 本研究过程包括以下基本步骤：搜集梳理相关文献—确定研究框架和工具—反复观看授课视频，将录像转化为文本信息—归类统计分析数据—得出结论.

4. 研究工具

本研究根据裴娣娜的教师教学行为分类和现场直播课的实际情况，确定编码系统和操作性定义，如表1所示.

本次研究教学行为采样的原则是：根据表1中的教学行为编码，结合陈老师的教学特点，以秒为单位对其教学行为进行时间记录和编码记录. 对于切换时间低于1秒的教学行为按照实际行为表现进行教学行为链的编码记录.

三、研究结果

1. 教学行为的质性研究

（1）教学行为清晰、逻辑性强.

在“因式分解”的教学活动中，陈老师的教学行为流程为：复习导入（观察、发现、类比）—因式分解的定义探究（观察、发现、归纳、一般抽象、练习）—因式分解方法的探究（观察、发现、归纳、一般抽象、练习）—课堂小结（总结—探究—留疑—布置作业）. 同时，陈老师引导学生探究时大多采用“提问—观察—指导—倾听—反馈”的行为链模式，始终以学生为主体，注重培养学生观察、发现问题、抽象概括的能力，运用联系的思想体现出数学知识的整体性，运用相同的“探究—发现”的学习程序总结了因式分解的定义和方法，使得学生能在一般观念的引导下，学会此类问题的研究思路和方法.

（2）教学行为的引导、联系性强.

“因式分解”对教师提出的一个挑战就是：如何让学生感觉因式分解不是“凭空蹦出来的”. 陈老师的教学行为多为引导性的，新的数学知识的从无到有都是建立在已有的知识经验的基础上的，注重对学生数学思维的培养，数学知识之间的联系性.

引出因式分解的定义的主要行为流程如下：提问整式运算;引导学生观察整式乘除运算的整体结构，发现未研究多项式除多项式的情况;提问如何研究多项式除多项式;陈述提示联系数的除法;提问多项式除多项式是否也存在结果仍为整式的特殊情况;用黑板展示数学例子;要求学生尝试计算并说明原因;类比因数的概念，提出因式分解的概念.

引出因式分解的方法的教学行为提炼如下：展示并提问因式分解和整式乘法之间的关系;提问从哪个角度入手研究多项式的因式分解;要求学生自己写出多项式因式分解的例子并展示;展示并要求学生进行归类;提问学生归类原因，找出运算的共同特点;总结出提公因式法和公式法的概念.

（3）教学机智不理想.

在数学课堂上，“预设”和“生成”是教师要注意调控的矛盾，当学生回答问题的答案不是教师想得到的结果时，怎样处理才能不打击该学生学习的积极性，又能让其他学生理解，这就需要教师的教学机智. 在教学过程中，学生的课堂表现有两次超出陈老师的预设：一次是陈老师提问因式分解和整式的乘法之间是怎样的关系时，有名学生回答“互逆”;另外一次是在课堂小结时，陈老师为了留疑，举出一个十字相乘的例子，并询问学生这是用什么方法解决时，一名学生回答“十字相乘”. 陈老师的回应仅自行歸因于学生进行了课前预习，未充分听取学生的想法，且指示下一名学生继续回答. 此类反馈行为会使该学生对“预习”产生一个怀疑的态度，且其他学生会下意识地将自己刚才自我总结的内容转化为“互逆”或“十字相乘”. 林祥华老师在进行点评时指出，陈老师不妨问一下回答的学生，他是怎样得出该结论的，转换角度，并在此基础上展开学生的数学思维过程.A69BFA2B-33B4-4ACE-9248-BAEE4E2F62E0

（4）组织学生讨论和练习的教学行为几乎未出现.

几乎没有给学生讨论的时间，节奏较紧凑，且因式分解的方法的探究环节没有呈现相应的练习题.

2. 教学行为的量化研究

本研究通过反复观看课程录像，将整节课的教学行为进行编码. 从整个教学过程来看，组织教学和复习导入、因式分解定义的探究、因式分解方法的探究、课堂小结四个教学环节所用时间所占的百分比为：15.97%，17.93%，47.76%，18.34%. 可以看出，陈老师将本节课的教学重点放在了因式分解方法的探究上. 接下來，本部分将按照四个教学环节，依次分析陈老师的各种教学行为的出现情况.

（1）组织教学和复习导入.

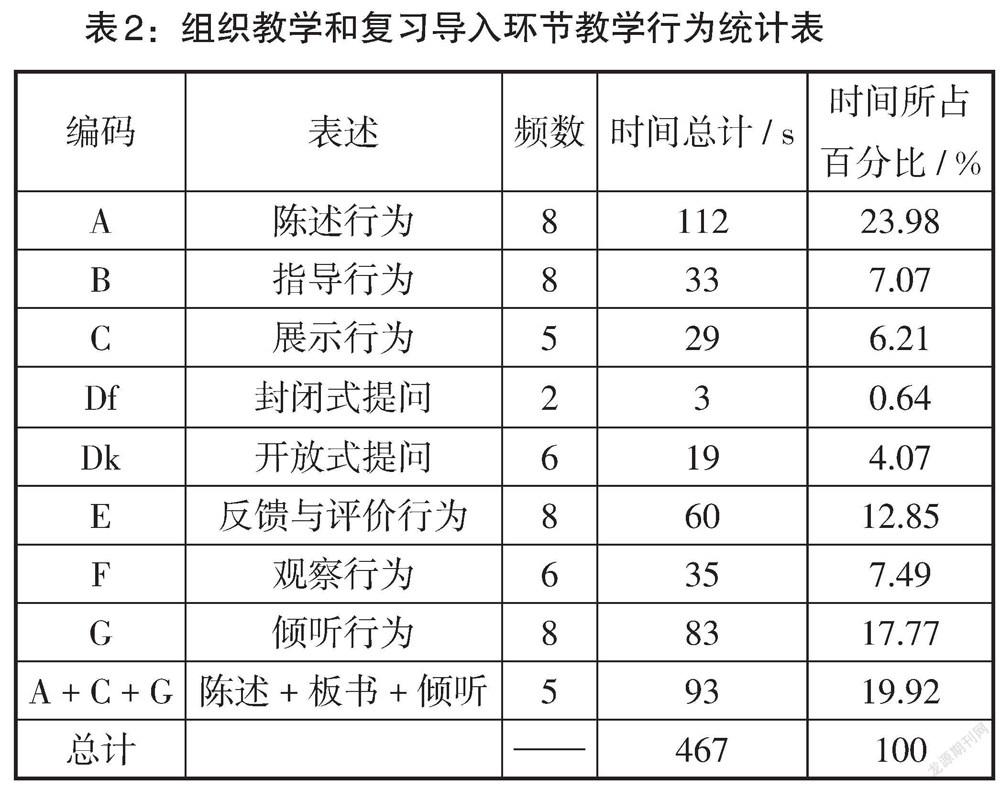
该教学环节的教学行为类型、频数、时间和时间所占百分比统计如表2所示.

由表2可知，陈老师在组织教学和复习导入环节用时为467秒，其中陈述行为所用时间最长，占总时间的23.98%;边陈述边板书边听学生附和的时间占到了19.92%，这表明以教师为主的讲授时间占据了43.9%. 提问行为多数为开放式提问（如“你有什么想提问的？”）. 虽然提问行为所占用的时间少，但频数为8，且提问、指导、倾听、反馈与评价总是伴随出现，该行为链是教师与学生互动的过程，所占时间百分比为42.4%. 观察行为总是出现在提问之后，8次提问中有2次未给学生思考的时间而直接提问.

该结果表明讲授在组织教学和复习导入教学环节占很大的比重，师生问答互动出现的次数较多，体现出陈老师充分利用提问行为引导学生思考，对于学生的回答总是及时给予反馈.

（2）因式分解定义的探究.

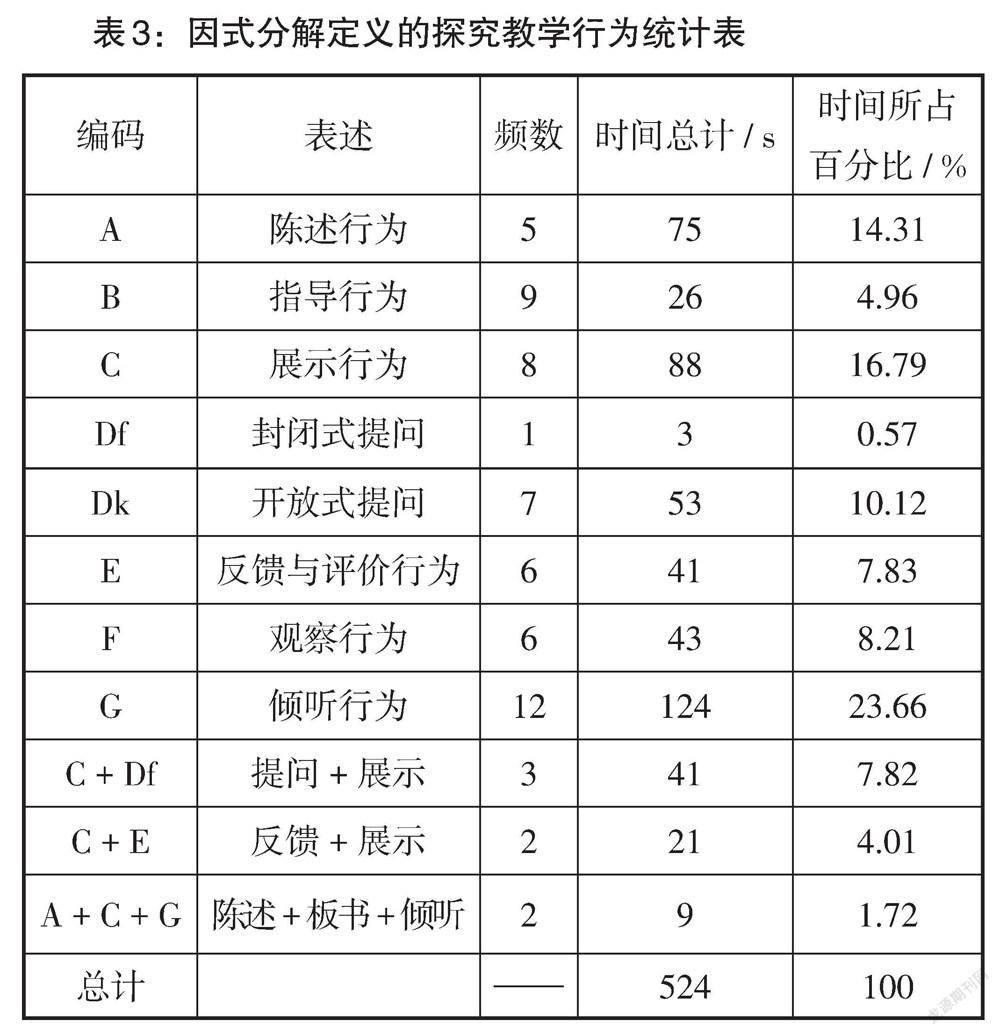
该教学环节的频数、时间和时间所占百分比统计如表3所示.

由表3可知，陈老师在因式分解定义的探究环节总用时为524秒，其中倾听行为所占时间最长，百分比为23.66%，表明陈老师在教学过程中注重学生的自我表达过程. 其次，陈老师的单独展示过程用时所占百分比为16.79%，这主要是陈老师在板书因式分解的定义所花费的时间. 此环节的提问次数为8次，开放式提问占了7次，表明陈老师仍然重视学生的自我想法的表达. 与上一个环节不同，陈老师有2次提问未给学生反馈：一次是学生的回答“超范围”;另一次是要求学生展示、学生评价. 此外，根据对实际课堂活动分析得出：在此环节的11个问题提出与解决的过程中有6次是按照“提问、指导、倾听、反馈和评价”的师生互动行为链开展的，可见该行为链的利用率较高.

（3）因式分解方法的探究.

该教学环节的频数、时间和时间所占百分比统计如表4所示.

由表4可以看出，陈老师在因式分解方法的探究环节花费1 396秒. 其中，倾听行为的时间所占百分比最高，是17.12%;其次是观察行为的时间，所占百分比为16.62%. 可以看出，陈老师在探究过程中十分注重学生的主导地位. 提问行为出现的频数仅次于倾听行为，共出现17次. 其中，封闭式提问共9次，主要是提问已学知识;开放式提问共8次，用于引导学生发现规律和方法. 同时，反馈与评价行为同步出现13次. 单独陈述和展示的教学行为出现频数较低，占用时间少. 此外，根据对实际课堂活动分析得出：在此环节的19个问题提出与解决的过程中有12次是按照“提问、指导、倾听、反馈和评价”的师生互动行为链开展的，可见该行为链的利用率较高.

（4）课堂小结.

该教学环节的频数、时间和时间所占百分比统计如表5所示.

由表5可知，陈老师花费536秒完成了课堂小结的工作，其中边展示PPT边陈述总结，并注意倾听学生附和的时间占据了70.71%，边展示PPT边陈述的行为占据3.54%，且没有单独的陈述或展示的行为出现，可知，陈老师此时主要以PPT展示教学内容，以与学生一起总结的行为为主. 提问行为中，封闭式提问居多，主要是提问学生已学内容，两个开放式问题是为了给学生留疑，让学生思考.

上述通过对陈老师教学行为的质性研究，得到了教师采用的教学方法、各阶段教学行为的顺序、联系、缺失等整体性特征，并分析了出现这些教学行为特征的原因，回答了“为什么”，但对于各环节哪种教学行为出现的频率最高，哪些行为链是多次完整的出现，哪些有所缺失，此类问题只能依赖于将教学行为编码并量化的方法. 基于表1的教学行为编码系统的量化研究发现各教学环节之间教学行为的出现频次有明显的差别，问题类型和行为链的构成也有明显的差别，为质性研究的结论再次提供了数据支撑，回答了“是什么”，但对于实际师生的活动互动的研究略显单薄. 故将上述质性研究的结果和量化研究的数据综合、对比分析，从不同层次的视角出发，有利于提高研究结论的可靠性和完整性.

四、研究结论与建议

1. 研究结论

（1）从整体教学过程来看.

① 教学重点在于因式分解方法的探究.

根据对各教学环节的数据统计可知，在此阶段的教学占据的时间最长，教师通过引导学生对不同特征的多项式的归纳，总结出公式法和提公因式法不同的适用情况.

② 教学行为清晰、逻辑性强，注重引导、联系性强.

根据对教师教学行为的梳理，发现陈老师采用了“单元—整体”教学法，探究程序严谨有序，有利于学生在一般观念的引导下提高自身的探究能力，加强对数学知识的整体性认识.

③ 教学行为以学生为本，构建民主课堂.

通过对教学行为的分析，发现陈老师重视通过提问引导学生思维，加强课堂对话，愿意花时间倾听学生的想法，师问生答的行为贯穿整个教学过程，并在大多数情况下给予一定的反馈.

（2）从各教学环节来看.

① 组织教学和复习导入环节以讲授为主，提问引导为辅. 提问以开放式问题为主，主要用来引导学生观察整式的运算结构，发现待解决的问题.A69BFA2B-33B4-4ACE-9248-BAEE4E2F62E0

② 因式分解定义的探究环节以提问、指导、倾听、反馈与评价的行为链为主，提问以开放式问题为主. 倾听行为给予学生更多自主思考和平等表达的机会，开放式问题能较好地激发学生的学习动机，让学生“顺理成章”地完成探究活动.

③ 因式分解方法的探究环节以提问、指导、倾听、反馈与评价的行为链为主要教学行为，封闭式问题和开放式问题并重，陳述行为明显减少. 封闭式问题有利于学生回顾和运用已学知识，同时开放式问题又有利于促进学生认知能力的发展，有利于知识结构的良好建构.

④ 课堂小结环节以借助PPT和黑板展示进行陈述，并注重倾听学生附和总结为主要教学行为，辅之以提问引导. 提问主要采用封闭式问题，让学生快速准确地回顾本节课的数学知识和探究思路，无孤立的陈述行为和展示行为出现.

（3）教学行为存在的不足.

① 教学机智不理想.

对“预设”和“生成”的矛盾处理得过于草率，未能尊重不同层次学生的学习表达.

② 忽视小组讨论，主要以点名提问的形式为主.

本节课教师没有指示学生小组或同桌讨论的行为，这不利于学生思维的碰撞和经验的交流. 提问都是以指示学生个体回答为主，且一个问题基本只指示一名学生回答.

③ 课堂教学中练习未得到足够重视.

本节课中只有一道例题，要求判断是否是因式分解.《义务教育数学课程标准（2011年版）》中“运用提公因式法、公式法（公式法运用不超过两次）进行因式分解（指数为整数）”的知识技能要求，在本节课中并没有相应的例题呈现，这不利于学生对因式分解方法的学习内容进行巩固和掌握.

2. 优化教师教学行为的建议

（1）合理预设，给予恰当的评价和反馈.

预设就像一只无形的手控制着教师的课堂教学，教师在课堂上的行为表现和行为流程都依赖于课前的教学设计. 仅设计了教学行为流程和提出的问题是不够的，还要“备学生”. 要针对学习能力和思维水平不同的学生，预设出他们的答案，给出不同的反馈和评价;预设出他们的困难，给出相应的解决策略.

（2）理解同构问题，多形式表达指令.

单纯地利用语言或数学符号来表述问题隔绝了数学与现实或其他学科的联系，单一的“对”与“错”的封闭式问答会造成学生随声附和. 智慧性与艺术性的行为是实现高效教学行为的重要保证，这就要求教师理解同构问题，向学生展示怎样利用不同的形式表征问题，采用多样的方式来表达自己的指令，以便让学生寻找到适合自己的表征问题的方式和更清楚地知道自己要做什么.

（3）重视生生互动，感知学生信息组织的限制.

经验不足的教师往往习惯于自己来确认学生的答案正确与否，这会导致师生双方的倾听、思考、质疑，以及考虑其他不同选择的能力降低. 教师应该重视学生之间的交流讨论，尊重他们自我表达的权利，教师可从生生互动中感知学生信息组织存在的限制，从发现课堂信息架构中未组织良好的部分加以优化.

参考文献：

[1]林正范，贾群生. 教师行为研究：课程与教学论的重要研究方向[J]. 教育研究，2006（10）：36-40.

[2]裴娣娜. 教学论[M]. 北京：教育科学出版社，2007.

[3]李松林. 课堂教学行为分析引论[J]. 教育理论与实践，2005（7）：48-51.

[4]余文森. 论教学中的预设与生成[J]. 课程·教材·教法，2007（5）：17-20.

[5]王光明. 高效数学教学行为的特征[J]. 数学教育学报，2011，20（1）：35-38.

[6]何光峰，曾志红. 新手教师与专家教师提问与理答行为差异的实证研究：基于12节初中语文阅读课的视频分析[J]. 中小学教师培训，2020（5）：37-42.A69BFA2B-33B4-4ACE-9248-BAEE4E2F62E0