超高速碎片云撞击下薄板变形与撕裂建模研究
刘泽荣,龙仁荣,张庆明,陈 利
(北京理工大学爆炸科学与技术国家重点实验室,北京 100081)
多层板结构广泛存在于航天器、舰船等结构中[1],然而航天器会遭受在轨超高速空间碎片的撞击,舰船等目标会遭受超高速动能武器的撞击[2]。在超高速弹丸撞击下,多层板结构中的第1 层板形成穿孔,第2 层及其后各层板则承受碎片云的冲击,即分布式载荷。碎片云的破坏形式与超高速弹丸明显不同,其破坏特征与尺寸是毁伤评估的重要参数,研究碎片云撞击下薄板的变形与破坏十分必要。
碎片云碰撞下薄板的变形与破坏可以看作薄板在具有空间分布的瞬态载荷下发生塑性动态大变形问题。薄壁结构是一种常见的结构,薄板变形理论由来已久,其中薄板小变形理论研究相对完善[3],而薄板动态塑性大变形理论仍在发展中。在研究薄板的大变形过程时,一方面需要同时考虑弯矩和膜力的作用,所建模型相对复杂,另一方面其几何方程具有非线性项,使得位移求解非常困难。Craggs[4]提出用薄膜理论分析薄板大变形,在模型中不考虑弯矩作用而只考虑膜力,这虽然可以简化理论模型,但是却只适用于很薄且强度较低的薄板大变形挠曲问题,难以描述常用金属薄板大变形问题[5]。Reissner[6]首先提出板壳大变形基本理论,随后Jones[7–8]应用此理论求解了理想刚塑性板在动载荷下的挠曲变形,通过忽略面内变形,从而简化方程得到理论解。Yu 等[9]引入膜力因子,将膜力对板变形的影响通过膜力因子乘以平衡方程中的弯矩体现出来,由于方程中不包含膜力项,求解薄板挠曲变形方程的难度大大降低。然而,这些模型忽略或简化了膜力作用,难以实现大变形高精度的计算。
本研究利用二级轻气炮开展球形弹丸超高速正撞击多层板实验,分析总结薄板在碎片云撞击下的变形与破坏特征,在此基础上建立考虑弯矩和膜力作用的环板变形模型,将大变形的薄板材料运动分解为横向的外凸运动和环向的膨胀运动,并结合Grady 破碎理论,建立环向膨胀花瓣撕裂模型。
1 超高速撞击多层板实验及结果分析
采用二级轻气炮将直径dp=9.13 mm 的LY12 铝合金球形弹丸加载至速度v0=5 km/s 后撞击多层板防护结构。多层板防护结构由4 块尺寸为100 mm×100 mm 的LY12 铝合金薄板组成,相邻两板间距为:S1=17 mm,S2=50 mm,S3=38 mm;第1 层至第4 层板的厚度分别为:hb1=1.0 mm,hb2=2.0 mm,hb3=2.0 mm,hb4=1.5 mm,如图1 所示。

图1 弹丸超高速碰撞多层板结构Fig. 1 Multi-shock shield structure subjected to hypervelocity impact
实验后各层板的照片如图2 所示,第1 层板只发生穿孔破坏,靶板中心有一个规整圆孔。第1 层与第2 层板的间距较小,弹丸与第1 层板碰撞形成的一次碎片云没能充分膨胀,碎片云载荷依然较为集中,因此第2 层板中央形成了一个大的穿孔,孔四周出现一个由小碎片撞击形成的环状小坑区域。第3 层板与第4 层板的破坏特征相似,板中间有穿孔破坏,孔周边材料发生拉伸完全变形,并且发生撕裂破坏,如图2(c)、图2(d)、图2(e)所示。第3 层板弯曲撕裂至靶板边界,边沿夹持的卡具也发生了弯曲大变形。由于第3 层板的阻挡,作用到第4 层板的碎片云能量大幅减小,第4 层板的弯曲变形主要集中在中部区域,边沿和卡具均没有明显的弯曲变形。由于裂纹扩展所需要的能量较小,第4 层板的裂纹依然扩展至靶板边沿。第4 层板表面覆盖一层白色物体,弹坑也相对较少,经分析,白色物是熔融铝冷却凝固物,熔融态的碎片云对第4 层板的作用更趋于整体作用,而不是大尺寸固态碎片的局部作用。整个多层板结构在超高速弹丸撞击下的变形特征如图1 所示。

图2 高速冲击后各层板的破坏照片Fig. 2 Damage results of each layer after hypervelocity impact
实验结果表明,弹丸与集中分布的碎片云撞击薄板会造成穿孔破坏,随着撞击次数的增加,弹靶材料破碎得更细,且熔融态的比例增加,碎片云载荷分布越分散,薄板的变形与破坏模式转变为中心穿孔及环孔区域大凹陷变形并伴有撕裂。第3 层板阻挡了大部分碎片云能量,第4 层板的弯曲变形比第3 层板小很多,其中心穿孔直径的测量平均值为46 mm,凹陷变形区域直径为穿孔直径的2~3 倍,凹陷板与靶板原平面的夹角较小,约为12°,说明其凹陷变形的速度较小。薄板穿孔四周材料的凹陷变形可简单类比成圆环的膨胀变形,当膨胀速度大于某值后,圆环在膨胀过程会断裂成多段。材料起裂后裂纹在板中传播形成长裂纹,与实验中薄板撕裂成多块的结果一致。根据前述分析,第4 层板环孔凹陷区域的变形速度较低,其环向膨胀更趋近于薄板起裂的临界速度。
2 碎片云作用下环形薄板变形模型
由实验结果总结得到在分散碎片云载荷下薄板的响应特征如下:薄板中间区域材料在碎片云中部高幅值冲击载荷下发生穿孔,环孔区域的环向板承受的碎片云载荷稍微小一点,环板材料发生凹陷变形,孔边材料在凹陷膨胀过程中破碎成几段,裂纹扩展直至薄板裂成几块。碎片云速度分布与环板变形如图3 所示。碎片云撞击薄板穿孔尺寸的计算已有研究[10],在此不做考虑,本研究侧重碎片云载荷下环形薄板的变形建模。
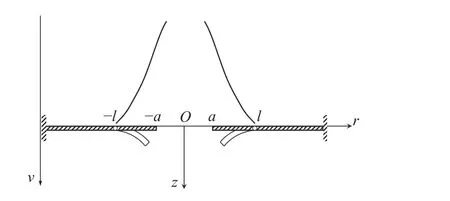
图3 环板变形侧视图Fig. 3 Lateral schematic of annular plate deformation
2.1 薄板变形假设与一般方程
根据实验结果可知,碎片云分布载荷作用下的变形属于典型的薄板大变形问题。薄板在变形过程中发生弯曲,需要考虑弯矩作用,另外薄板面内还有膜应力。要建立薄板变形的一般方程,需作如下基本假设:
(1) 考虑到薄板挠度是板厚的几倍甚至几十倍,为此忽略板的弹性小变形,采用理想刚塑性体模型描述薄板变形;
(2) 薄板变形服从Love-Kirchhoff 假设[11],即中面法线变形后仍保持为中面法线,厚度变化忽略不计,同时略去中面法向应力;
(3) 不区分变形前后参考位形的差异,采用变形前的位形作为参考基准建立平衡方程;
(4) 薄板内力除径向弯矩Mr和环向弯矩Mθ外,还需要考虑径向膜力Nr和环向膜力Nθ。
基于以上假设,可以建立轴对称薄板变形过程的横向、环向和径向动力学方程[12]
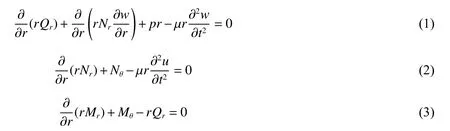
式中:r为径向坐标,θ 为环向坐标,u为径向位移,w为挠度,Qr为剪力,µ为板的面密度,p为轴对称的横向分布载荷。
考虑面内变形与出面变形的薄板轴对称几何方程,其内力(或称广义应力[3])径向弯矩Mr、环向弯矩Mθ、径向膜力Nr和环向膜力Nθ对应的广义应变分别为径向膜应变εr、环向膜应变εθ、径向曲率κr和环向曲率κθ。几何方程如下

采用理想刚塑性体模型,材料发生刚性位移或塑性变形,则薄板发生塑性变形时膜力Nr、Nθ达到N0,弯矩Mr、Mθ达到M0

式中:h为板厚度,σy为屈服强度。
薄板材料是理想刚塑性体模型,薄板的应力状态位于屈服面上,为此采用Hodge[13]提出的包含弯矩、膜力作用的近似屈服准则,如图4 所示。可以看出,屈服面上的膜力和弯矩独立作用,各自位于Tresca 屈服面上。这样的近似处理使求解过程变得非常简便。另外,横向剪力Qr出现在平衡方程中,但是由于不考虑其产生的剪切变形,因此不出现在屈服条件中,并且后面计算中可以看到,化简的平衡方程不包含剪力。
图4 中mr、mθ、nr、nθ为无量纲内力,mr=Mr/M0,mθ=Mθ/M0,nr=Nr/N0,nθ=Nθ/N0;A、B、C、D、E、F是屈服条件上的角点,各线段代表材料的某一内力状态。正交法则规定一点广义塑性应变增量的方向与屈服面外法线方向相同,如图4 所示。对于具体的问题,在约束允许的机动场中,根据广义塑性应变增量(或广义塑性应变率)的方向,可以确定塑性变形由哪一部分屈服面控制,从而为具体问题的求解确定内力大小。

图4 Tresca 屈服条件与正交法则Fig. 4 Tresca condition and flow rule
2.2 环板变形方程简化
根据薄板变形方程,结合屈服条件和正交法则,就可以求解薄板变形的初边值问题,从而得到环板的变形。然而多个偏微分方程的相互耦合以及非线性项的引入,使方程很难得到解析解,需要根据本问题的特征对方程进行简化。理想刚塑性体的使用、碎片云撞击载荷的特性以及环板构型的特殊性会使方程变量减少,复杂程度降低。
如图5 所示,薄板中部发生穿孔(0

图5 环板变形俯视图Fig. 5 Top schematic of annular plate deformation
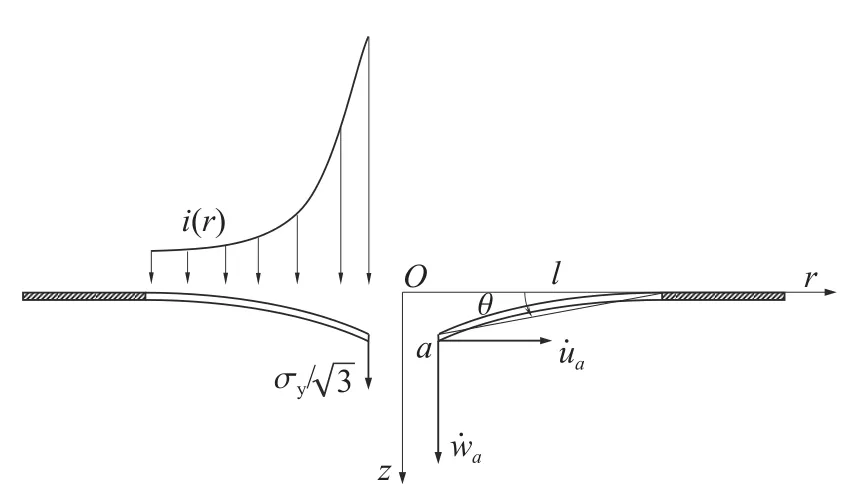
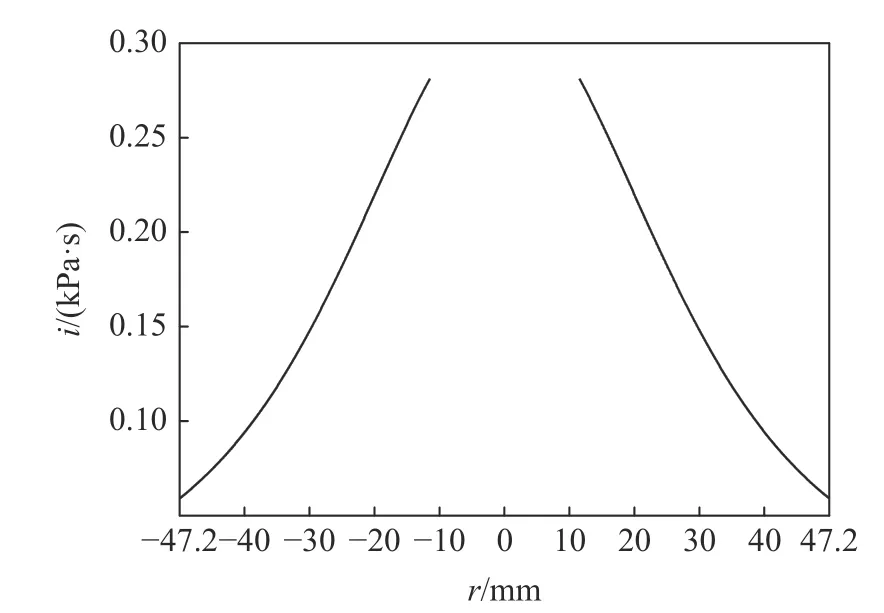
刚塑性环板挠曲变形采用锥形机动场[14],即a≤r 代入式(14),得 由于只有单一未知量,使用能量方程微分形式求解更方便,即塑性铰上塑性功率与动能变化率平衡 对于a 代入式(34)得到环板凹陷变形终态角度θt 由式(33)和式(34)即可求出环板变形最终挠度wta和终态角度θt,由式(29)可得到环板变形与速度的关系式。下面将计算环板在碎片云撞击下的具体变形问题,得出环板径向速度,进而计算环板花瓣型撕裂。 图6 挠度与径向关系示意图Fig. 6 Schematic of relationship between deflection and radial displacement 图7 冲量载荷下环板变形示意图Fig. 7 Deflection of annular plate subjected to impulse 为计算环板撕裂起始时的变形,首先计算出环板在碎片云撞击下达到的最大径向速度。为得到环板变形时材料受力状态,将板厚h= 1.5 mm、材料屈服强度 σy= 265 MPa 代入式(8),求得刚塑性弯矩M0和刚塑性膜力N0。根据多次碎片云模型[10],可以计算本研究实验工况下3 次碎片云对第4 层环板施加的冲量面密度i(见图8)以及碎片云作用范围的半径l= 47.2 mm,再通过式(30)~式(32)求得碎片云撞击环板时环板的初始动能Ed0= 97.5 J。由式(29)和式(17)得到内环边径向速度u˙a随内环边挠度wa变化曲线,如图9 所示,得到最大内环边径向速度u˙ma为25.99 m/s。 图8 冲量面密度载荷分布曲线Fig. 8 Distribution of the impulse per area 图9 环板内环边径向速度与挠度的关系Fig. 9 Relationship between inner edge radial velocity and deflection 上述模型可以用于描述碎片云载荷分布较分散的环形薄板变形,其环板凹陷变形区域集中在碎片云载荷分布区域内,由于载荷不太集中,环板的变形不太快,变形区与未变形区分界的塑性铰采用驻定塑性铰,其计算结果与第4 层板的实验结果相符合。实验中二次碎片云撞击第3 层板时的冲量面密度相对较高,第3 层板凹陷变形的速度较快,拉着未变形区域发生凹陷,其变形区与未变形区的塑性铰是移动的,因此第3 层板的变形需采用移行的塑性铰圆来描述。对于移行铰,l=l(t),l˙ ≠0,由图6 可知,这时内环边挠度wa和径向位移ua为 通过超高速撞击实验总结了薄板在轴对称碎片云载荷作用下的变形与破坏模式,并对此完成了建模研究,结论如下: (1) 实验中薄板在分散的碎片云载荷下经历中部穿孔,形成环板,环板在剩余碎片云载荷下发生凹陷,孔边材料继而发生拉伸破碎,形成花瓣型撕裂; (2) 基于实验现象与经典理论,建立了环形薄板在碎片云冲击下的刚塑性变形模型,该模型同时考虑弯矩和膜力,通过简化得到了环板变形微分方程,可以求解得到板横向速度场和径向速度场; (3)将孔周边的薄板材料膨胀视为圆环的膨胀,根据模型计算得到环板内环最大环向应变率,代入Grady 破碎模型,计算实验中第4 层板撕裂的花瓣数,另外根据模型还计算得到环板凹陷变形终态角度,计算结果均与实验结果吻合; (4) 对于高幅值碎片载荷的环形薄板变形,宜采用移行塑性铰描述变形区域的扩展过程,其变形的理论建模和求解还需要在本研究的基础上进一步开展。
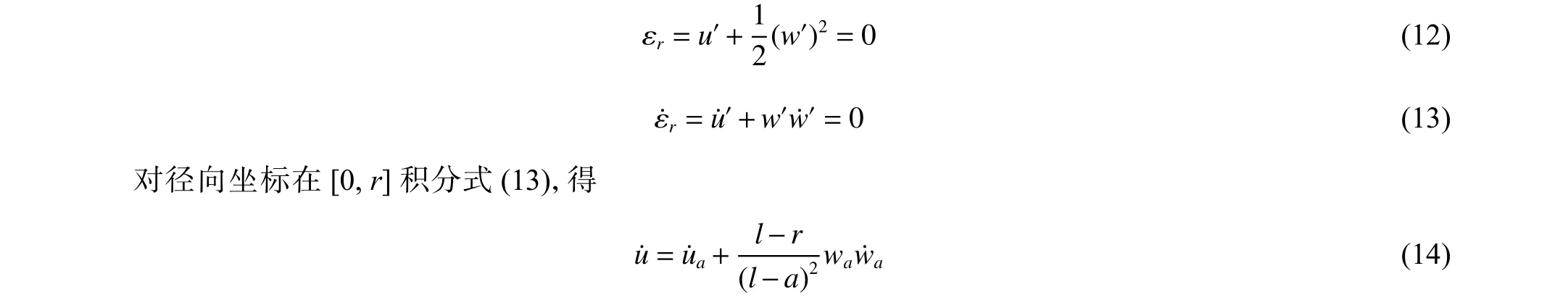



2.3 动力学方程求解



3 计算验证






4 结 论

