率温联合条件下混凝土材料压缩强度的变化规律
李 平,孙崇慧,黄瑞源,段士伟
(1. 安徽工业大学机械工程学院,安徽 马鞍山 243032;2. 南京理工大学瞬态物理国家重点实验室,江苏 南京 210094)
混凝土结构具有抗冲击、抗高温、抗爆炸的优势,在国防建设和民用工程中有着广泛应用。现代局部战争中高新科技常规武器的研发和恐怖主义事件中大规模杀伤性破坏武器的使用,对于各国防御工事的防护能力都是很大的挑战。战后现场表明,火灾、爆炸等引起的高温和强冲击脉冲是导致大型钢纤维混凝土防护结构破坏的主要原因,且高温和冲击载荷往往相伴发生。因此,开展率温联合条件下混凝土材料压缩强度变化规律研究是非常必要和重要的。
混凝土材料的压缩强度既具有明显的应变率强化(硬化)效应,又具有明显的温度弱化(软化)效应。当前,在常温下,一般采用应变率增强因子,即混凝土的常温动态强度与常温准静态强度之比( σd0/σs0)来描述应变率强化效应[1–7];在高温准静态下,一般以温度弱化因子,即混凝土的高温准静态强度与常温准静态强度之比( σsT/σs0)来描述温度弱化效应[8–19];而在高温和动载联合作用下,有些学者主要关注不同温度下应变率的影响,采用同一温度下的动态强度与准静态强度之比( σdT/σsT)来描述高温下的应变率强化效应[20];有些学者则关注高温和应变率对强度的综合影响,采用高温下的动态强度与常温下的准静态强度之比( σdT/σs0)来描述率温联合效应[21]。本研究采用联合效应因子K,即高温下的动态强度与常温下的准静态强度之比( σdT/σs0)来描述应变率和温度对压缩强度的影响。
对于混凝土材料在单一温度或应变率( ε˙)条件下的性能研究,从最早公开发表的文献[22]来看,已经有超过百年的历史。但是对于混凝土材料压缩强度在应变率和温度联合作用下的探讨,却是从21 世纪初才真正得到关注。从文献检索结果来看,对于混凝土材料在率温联合条件下的研究,我国学者在国际期刊上公开发表的文献数量多于国外学者。近年来,良好的实验条件和充足的科研经费为我国学者开展率温联合下的研究提供了强有力的支持,诸多学者也取得了有价值的成果[20–21,23–33]。目前,虽然动态实验技术已经较成熟,但在混凝土动态实验研究中仍然存在一些争议,如试件尺寸和形状差异对实验结果的影响、大口径分离式霍普金森压杆(split Hopkinson pressure bar, SHPB)实验结果的离散性和随机性较大,此外还有结构效应、摩擦效应等问题[3,30]。而高温的介入又带来了新的问题:(1) 大量实验研究已经证明,单一条件下,应变率增大(特别是应变率较高时),材料强度将显著升高,而温度升高时,材料强度会显著降低,如果增加应变率的同时提升环境温度,那么混凝土压缩强度是升高还是降低,即应变率和温度对压缩强度的影响是否有主次之分;(2) 应变率强化效应和温度弱化效应对压缩强度的影响是否是相互独立的,即应变率和温度对压缩强度的影响能否用率温解耦的形式来描述;(3) 如果应变率强化效应和温度弱化效应对压缩强度的影响是耦合的,应当如何描述二者的耦合规律和内在关系。针对第1 个问题的争议较大。有些学者[32,34]认为,高温动态条件下温度弱化是混凝土材料性能的主要影响因素,应变率强化是次要因素。但文献[31, 35]的研究显示,在率温联合条件下,压缩强度因子虽然随温度升高而降低,但却始终大于1,即率温联合条件下的混凝土压缩强度大于常温准静态下的压缩强度,这说明应变率强化是主要因素,而温度弱化是次要因素。针对第2 个问题的争议较少。尽管当前广泛使用的混凝土本构模型[36–37]和大型计算软件[38]仍然采用解耦的形式来描述率温联合条件下混凝土材料强度的变化规律,但是学者们普遍认为应变率效应和温度效应在材料内部是相互影响、相互耦合的,诸多实验结果[20–21,23–29]也证实了这一观点。第3 个问题是以第2 个问题中率温效应相互耦合为前提的,从当前收集到的文献来看,对率温耦合规律和内在关系的数学表述还未见公开报道。由于高温动态实验对实验设备和操作人员的要求更高,并且加热方式的选择、加热速率的控制、达到预设温度后的恒温保持时间的设定以及材料内部各相(水泥砂浆、粗骨料以及二者之间的界面区)在加热过程中伴随着的一系列物理和化学反应等因素均会对实验结果产生影响,使得实验数据较常温下的离散性更大,因此混凝土率温联合条件下的热动力学行为研究起步较晚,收集到的文献较单一应变率或单一温度条件下的文献数量偏少。尽管如此,虽然学者们的实验结果存在一些离散性和差异,但是混凝土材料本身的热动力学行为特点仍然呈现出明确的规律性。
整理近30 年的高温动态实验数据,并摒弃一些实验结果明显偏离的文献,在总结归纳实验数据的基础上,针对上述3 个问题,探讨率温联合条件下的压缩强度变化因子K的变化规律,拟合得到不同温度下的K- ε˙关系方程;确定应变率强化和温度弱化分别成为主导影响因素的率温条件,划分应变率强化效应主导区域(满足该区域率温条件的混凝土材料压缩强度高于常温静态下的压缩强度)和温度弱化效应主导区域(满足该区域率温条件的混凝土材料压缩强度低于常温静态下的压缩强度);得到应变率效应和温度效应的内在关系方程,确定混凝土材料率温相当表征参数。此外,本研究只考虑干燥混凝土,浸水混凝土不在本研究范围内。
1 混凝土材料压缩强度在不同应变率和不同温度下的率温联合效应
诸多研究表明,混凝土试件的动态压缩强度具有明显的应变率强化效应[1–7,39–42],尽管有学者认为,混凝土试件在高应变率下呈现出的应变率强化效应主要是由侧限效应或横向惯性以及动静态试件差异导致的尺寸效应等原因造成的,而材料本身的应变率强化效应比实验测试结果小得多,但这些争论仅限于应变率强化效应的程度,并未明确否认应变率效应存在这一事实[3,30]。实验证明,动态高温下的混凝土试件仍然呈现出与常温下类似的应变率强化效应[20–30]。
材料的温度弱化效应(流动应力随温度升高而降低)是早于应变率强化效应而为人们所熟知的[43]。从已发表的实验数据来看,混凝土高温实验的测试温度范围一般在20~800 ℃,当温度超过800 ℃时,混凝土试件几乎不再具备承载能力或仅有少许承载能力,但实验数据较少,且实验结果的差异性较大。因此,本研究主要针对温度不高于800 ℃条件下混凝土材料的动静态压缩强度数据进行分析,以确定率温效应对混凝土材料压缩强度的影响。
定义率温联合效应因子K= σdT/σs0,该因子可以反映温度和应变率联合条件下材料压缩强度的变化规律。当K> 1 时,即混凝土材料率温联合下的压缩强度高于常温准静态下的压缩强度,说明在应变率强化和温度弱化两种影响因素的相互竞争中,应变率强化效应占据主导地位;当K< 1 时,即混凝土材料率温联合下的压缩强度低于常温准静态下的压缩强度,说明在应变率强化和温度弱化两种影响因素的相互竞争中,温度弱化效应占据主导地位;当K= 1 时,即混凝土材料率温联合下的压缩强度等于常温准静态下的压缩强度,说明混凝土材料在应变率强化和温度弱化两种影响因素的相互竞争中,应变率强化和温度弱化效应对压缩强度的影响相当。
收集整理文献中的混凝土材料高温动态实验数据,如图1 所示。其中试件形状均为圆柱体,括号内的标注为试件尺寸。尽管不同文献的实验数据之间存在一定的偏离和差异,但从总体来看,各文献中率温联合效应因子-应变率-温度(K- ε˙-T)三者之间的关系所呈现的规律是一致的。
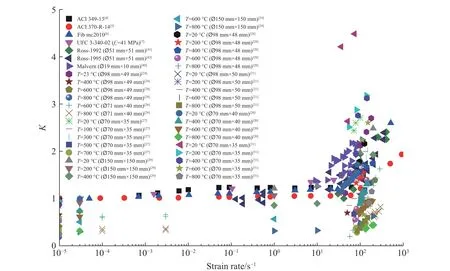
图1 在不同温度和不同应变率下混凝土材料压缩强度的率温联合效应Fig. 1 Joint effect of rate-temperature on compressive strength of concrete at different temperatures and strain rates
对实验数据进行拟合,得到不同温度和不同应变率下的K- ε˙关系曲线,如图2 所示。将图2中的高应变率部分局部放大,如图3 所示。将拐折点处进一步放大,如图3 插图所示。
由图1、图2、图3 可以看出,混凝土材料压缩强度的率温联合效应因子K具有以下特点。
(1) 与常温下的动静态实验结果类似,不同温度下,K随应变率的变化可划分为两个区域,如图2 和图3 所示,拟合曲线呈现明显拐折。拐折点处的应变率称为拐折应变率 ε˙in,当ε˙ < ε ˙in时,混凝土材料在各个温度下均未表现出明显的应变率强化效应,仅表现为温度软化效应,不同温度下K-ε˙拟合曲线斜率较小,K随 ε˙的变化速率均较慢;当ε˙ >ε ˙in时,K-ε ˙拟合曲线斜率较大,K随应变率ε˙的变化速率显著加快,呈现出明显的应变率强化效应。拟合曲线的拐折表明,应变率达到拐折应变率( ε˙ > ε ˙in时)后材料内部的塑性流动机理发生了本质变化。

图2 混凝土材料在不同温度和不同应变率下的K- ε˙关系Fig. 2 Relationship of K- ε˙ of concrete at different temperatures and strain rates

图3 高应变率部分以及拐折点处K 随应变率的变化规律Fig. 3 Variation of K with strain rate at high strain rate and the turning point

(4) 不同温度下拟合曲线的拐折点不同,拐折点随温度的升高而后移,即拐折应变率 ε˙in随着温度升高而增大,温度越高,应变率效应滞后越明显,不同温度下混凝土发生“冲击强化”现象存在时间(应变率的倒数)差。拐折应变率随温度变化的拟合曲线如图6 所示,该曲线反映了混凝土材料在高温动态载荷作用下呈现显著应变率效应时(即压缩强度对应变率的变化较敏感)的拐折点与温度之间的关系。可以发现, ε˙in-T拟合曲线将图6 分为两部分:曲线以上的区域为应变率敏感区,温度和应变率的坐标点落在应变率敏感区时,混凝土的压缩强度表现出显著的应变率效应;曲线以下的区域为应变率不敏感区,温度和应变率坐标点落在不应变率敏感区时,混凝土的压缩强度仅表现出温度弱化现象,应变率效应不明显。为使方程量纲统一,对温度和应变率进行无量纲化处理,得到拟合曲线方程为
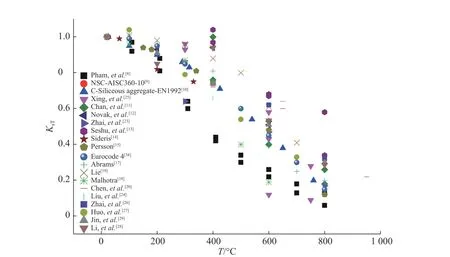
图4 混凝土材料在准静态条件下的温度弱化效应Fig. 4 Temperature weakening effect of concrete under quasi-static condition
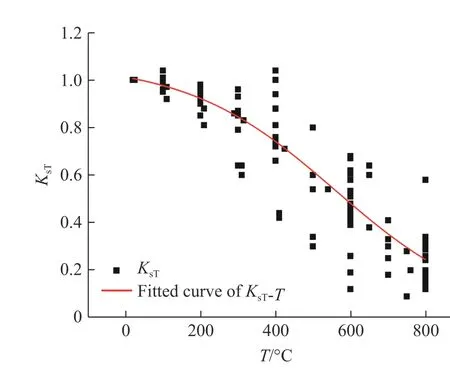
图5 温度弱化因子随温度的变化曲线Fig. 5 Curve of temperature weakening factor varying with temperature
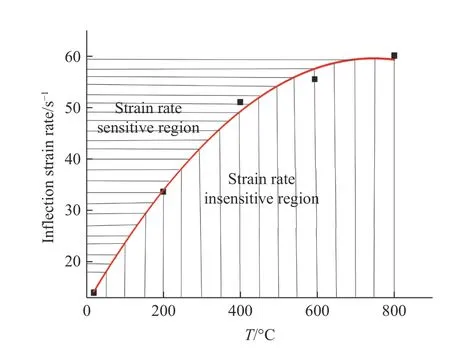
图6 温度T 与拐折应变率ε ˙in 之间的拟合关系曲线Fig. 6 Fitting curve between temperature and inflection strain rate ε˙in

式中:无量纲参数T*=T/T0, ε˙∗= ε ˙in/ε ˙0,取T0= 20 ℃, ε˙0= 1 s−1。
(5) 由实验数据拟合得到混凝土压缩强度的率温联合效应因子K在各温度下随应变率的变化规律。
当ε˙<ε ˙in时,率温联合效应因子K随应变率ε˙变化的关系方程为


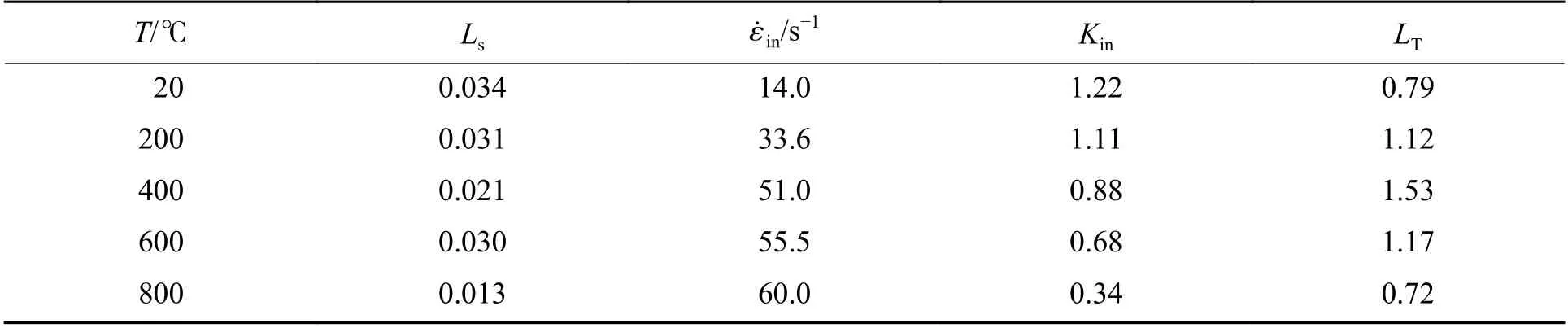
表1 K-ε˙拟合方程中的相关参数Table 1 Relevant parameters in K- ε˙ fitting equation
由拟合结果可以发现,在温度和应变率联合作用下,K随应变率变化的速率在拐折点前后相差较大,22Ls
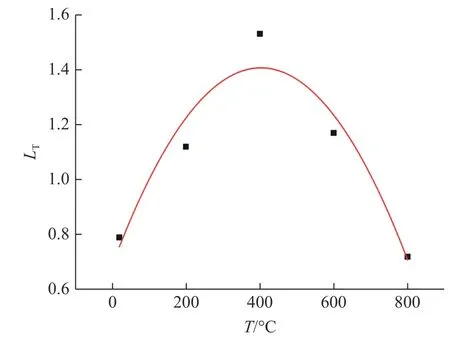
图7 当ε˙ > ε ˙in 时率温联合效应因子变化速率与温度的关系Fig. 7 Relationship between temperature and change rate of combined effect factor of strain rate and temperature when ε˙ >ε ˙in
2 混凝土材料的率温耦合效应分析
采用目前广泛使用的一些材料本构模型和计算软件分析率温联合作用下材料的热力学响应时,一般是按照温度效应和应变率效应相互解耦的方式进行,如在Abaqus 等大型计算软件[39]中广泛采用的Johnson-Cook 本构模型[36–37],其方程表达式为
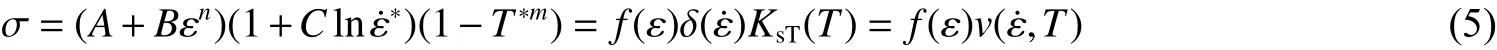
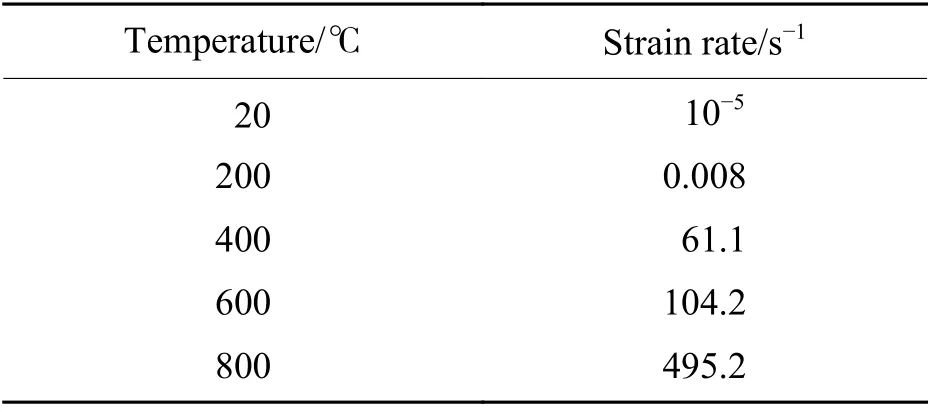
式中:A、B、C、m、n均为材料常数, δ ( ε˙)、KsT(T)和v( ε˙,T)分别代表应变率强化效应、温度弱化效应以及率温联合效应对材料应力的影响。其中KsT(T)的表达式通过准静态高温实验数据拟合得到,而δ ( ε˙)的表达式由常温动静态力学实验数据拟合得到,KsT(T)与δ ( ε˙)均通过单一实验条件(温度或应变率)得到,二者相互独立,互不影响。该模型虽然同时考虑了应变率强化效应和温度弱化效应的影响,但却是以率温解耦形式建立的本构方程,且未证实材料在高温与冲击载荷联合作用下,按照率温解耦形式建立本构模型的合理性。事实上,大多数材料在高温与冲击载荷联合作用下,温度弱化效应和应变率强化效应之间存在密切的内在关联,并且有些材料(如铝、软钢等)存在率温等效现象[44–45]。历史上,人们首先关注在低应变率下的力学响应在时间相关性和温度相关性之间是否存在某种转换或等价关系,即所谓的时温等效性,发现通过改变时标(在时标上移动lgα(T)),可以使一个温度下的黏弹性行为和另一个温度下的黏弹性行为相叠加,α(T)称为移位因子,仅为温度的函数[46],混凝土材料在低应变率下的压缩强度变化也有类似现象,如图2 所示。各温度下的压缩强度变化因子K曲线在拐折点之前,应变率效应均不明显,K-lg ε˙几乎都是平行的(斜率Ls≈ 0.02,0.01 为了进一步确定混凝土材料压缩强度的率温耦合效应,首先借鉴Johnson-Cook 本构模型对温度和应变率的描述方式,若率温效应是解耦的,那么率温联合效应因子可以表示为 式中: δ ( ε˙)和KdT分别为常温下和温度T下的应变率效应因子。 当应变率较低( ε˙ < ε ˙in)时, δ (ε ˙)、KdT的值均很小,有些学者忽略二者的区别,用同一拟合曲线代替[20];当应变率较高( ε˙ > ε ˙in)时,δ(ε ˙)、KdT的值均显著增大,且二者变化又明显不同,由图2、图3 以及式(3)、式(4)可以发现, ε˙ > ε ˙in时,各温度下的K-ε ˙曲线变化速率(拟合线的斜率)明显不同,变化速率如图7 所示,故δ (ε ˙) ≠KdT。 根据上述实验数据和拟合结果,将各温度下的K-ε ˙曲线和δ·KsT-ε ˙曲线进行对比,如图8 所示,由图8可以清楚地看出各温度下的K- ε˙曲线和δ·KsT- ε˙曲线均存在较大差异,故K≠ δ·KsT,则应变率强化效应和温度弱化效应并非是解耦的,而是相互耦合的,因此率温联合效应因子K不能解耦地表述为单一实验条件(应变率或温度)下得到的应变率效应和温度效应的点积。这一结果在文献[47]也有相同结论。 图8 各温度下的K- ε˙曲线和δ·KsT- ε˙曲线的对比Fig. 8 Comparison of K- ε˙ curves and δ·KsT-ε ˙ curves at different temperatures 为了得到压缩强度的应变率效应和温度效应之间的内在关系,需要进一步分析K-ε˙-T三者间的变化规律,根据K的定义,当K= 1 时,混凝土压缩强度的应变率强化效应和温度弱化效应相当,混凝土在满足K= 1 的率温条件下的压缩强度与常温准静态下的压缩强度相等。由式(1)、式(2)求得各温度下K= 1 时的应变率,如表2 所示。将满足K= 1 时的温度和应变率关系进行拟合,得到的曲线如图9 所示。率温条件落在曲线以上时,K> 1,此时材料表现为强化现象,压缩强度高于常温准静态下的压缩强度;反之,率温条件落在曲线以下时,K< 1,此时材料表现为弱化现象,压缩强度低于常温准静态下的压缩强度。 图9 K=1 时温度和应变率的关系曲线Fig. 9 Relation curve between the temperature and the strain rate when K=1 表 2 K=1 时各温度下的应变率Table 2 Strain rates at different temperatures when K=1 拟合得到K= 1 时的温度和应变率关系方程 式中: ε˙∗= ε˙/ ε ˙0, ε˙0= 1 s−1,T*= (T − T0)/T0,T0= 20 ℃,a=4.98 × 1012,b= 2.63 × 1012,p= 0.14。满足该方程的率温条件关系时,混凝土材料压缩强度和常温准静态下的压缩强度相等,即温度弱化与应变率强化相互竞争的结果是二者对压缩强度的影响相当,相互抵消;在该曲线以下的区域,温度弱化效应占主导地位,压缩强度小于常温准静态下的压缩强度,即K< 1,处于该区域的率温条件可以通过提高应变率或者降低温度来回归到K= 1 的率温平衡曲线上;相反,该曲线以上区域为应变率强化效应占主导地位,压缩强度大于常温准静态下的压缩强度,即K> 1,处于该区域率温条件下的混凝土材料可以通过降低应变率或者提高温度来回归到K= 1的率温平衡曲线上,因此式(3)也可称为混凝土材料率温等价关系方程。 引入参数Z*,令 只要率温条件满足Z*= 1,随意改变应变率和温度条件,应变率强化效应和温度弱化效应仍然相当,即K= 1;当Z*> 1 时,应变率强化效应是影响强度变化的主要因素,此时K> 1;当Z*< 1 时,温度弱化效应是影响强度变化的主要因素,此时K< 1。因此,由参数Z*的值即可判断联合效应因子K所在的区间。该参数反映了应变率强化效应和温度弱化效应之间的作用规律,故将Z*称为混凝土材料率温等价参数。本研究从宏观热动力学响应得到的参数Z*与Zener 等[48]基于位错动力学提出的Zener-Hollommon 率温等价参数在形式相似,Zener-Hollommon 参数Z= ε˙eU/(λT),其中,U为热激活能, λ为材料常数。由于热激活能很难从实验中直接得到,因而本研究定义的率温等价参数相较于Zener-Hollommon率温等价参数更便于工程应用。 基于当前收集到的混凝土热力学性能测试结果,分析了应变率和温度对压缩强度的耦合影响,以及率温联合效应因子K随温度和应变率的变化规律,得到如下结论。 (1) 准静态下,温度弱化效应显著,弱化因子KsT与温度T之间的关系式为KsT=a/{1+e−m[(T−T0)/T0−n]}。 (2) 温度对应变率效应有滞后作用,率温联合条件下应变率敏感区与不敏感区的界限曲线为 ε˙*=11.66 + 2.56T*– 0.03T*2,曲线以上的率温区域为应变率敏感区,曲线以下的率温区域为应变率不敏感区,仅表现出温度弱化现象。 (3) 拟合得到K的表达式:当ε˙ < ε ˙in时,K-ε ˙的关系方程为K=KsT+Ls[lg(ε ˙ /ε ˙0)−lg(ε ˙s/ ε ˙0)];当ε˙ > ε ˙in时,K- ε˙的关系方程为K=Kin+LT[lg( ε˙ /ε ˙0) − lg(ε ˙in/ε ˙0)]。 (4) 给出了率温联合条件下应变率强化效应和温度弱化效应在对压缩强度的影响中占据主导地位的区域,建立了率温效应影响相当(K= 1)时的应变率和温度内在关系方程为 ε˙*=a/(1 +be−pT*),得到了便于工程应用的混凝土材料率温等价参数Z*= ε˙∗(1 +be−pT*)/a。


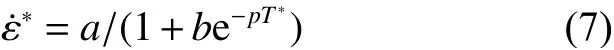

3 结 论

