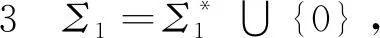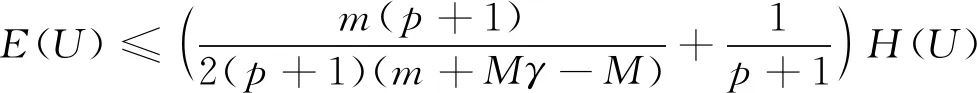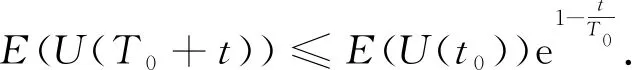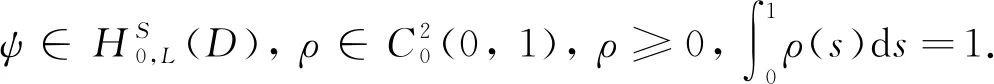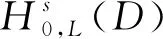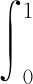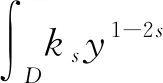一类半线性分数阶反应扩散方程解的整体存在性①
彭红玲,樊明书
西南交通大学 数学学院, 成都 610031
随着科学的发展, 经典Laplacian方程Δu=0不适合生活中很多复杂的物理问题, 特别是大范围不规则的扩散现象, 由此人们提出了分数阶Laplacian算子. 从概率论的角度看, 分数阶Laplacian算子是稳定Lévy过程中的无穷小生成元, 是Lévy飞行过程中的尺度极限[1-2], 它在金融数学、 概率论、 生物学等领域中有着广泛的应用[3-5].
常见分数阶Laplacian算子的定义有3种, 根据Riesz位势给出的定义[6]、 根据傅里叶变换给出的定义[7]以及利用函数延拓给出的等价定义[8]. 本文用文献[8]中的定义.
文献[9]研究了半线性抛物方程ut=Δu+V(x)up在Dirchlet条件下的爆破, 其中Ω是RN中的光滑有界凸区域,M≥0,V是Lipschitz连续的,φ>0且φ满足相容性条件.
(1)
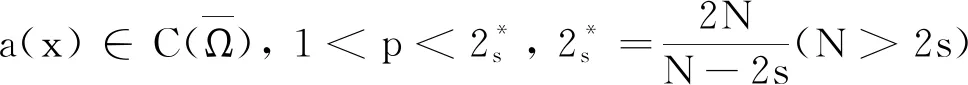

D={(x,y)|(x,y)∈Ω×(0, ∞)}
D的横向边界为∂LD=∂Ω×[0, ∞), 将方程(1)化为
(2)
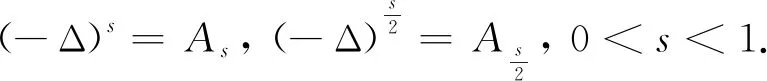
(3)
其中
这里
同理方程(1)的能量泛函定义为
(4)
受文献[13-16]的启发, 定义
对E(U(t))关于t求导, 得
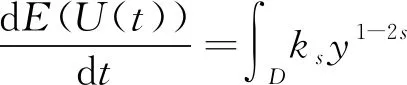
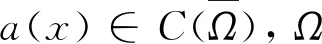
定义势井的深度为
本文的主要结果如下:
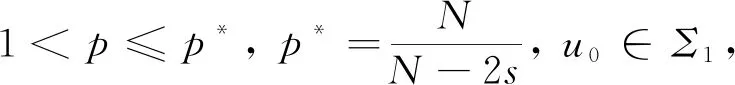
定理2若U=U(x,y,t;U0)是方程(2)的解, 且U0∈Σ1, 则存在α>0, 使得
1 解的整体存在性
为证明定理1, 先引入引理1、 引理2, 其证明过程与文献[12]中的相关结论的证明类似, 此处省去证明.
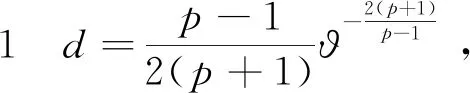
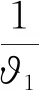
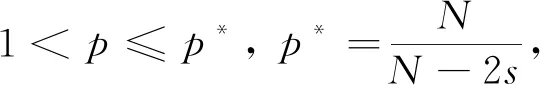
(5)

定理1的证明.
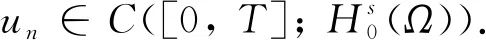
(6)
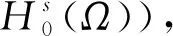
这也与(6)式矛盾. 所以∀t∈[0,T],un(t)∈Σ1. 由Σ1的定义, 有
(7)
即有
由(7)式, 可得
令
由引理1和I(u0)+ε0 令γ=1-δ∈(0, 1), 则有 (8) 所以方程(1)存在整体解. 在本节中, 为证明定理2和定理3, 先引入引理3, 其证明过程参见文献[12]. 定理2的证明. 由引理3, 对∀t≥0, 有H(U(t))≥0. 则 (9) 由分数阶Sobolev迹嵌入不等式, 有 (10) (11) 在(11)式中, 对任意的T>t0, 由Hardy不等式[18]有 (12) 所以, 当t∈[t0,T)时, 结合(9)式和(12)式有 (13) 由(10)式知, 当t∈[t0, ∞)时, 有 (14) 结合(9)式和(14)式可知, 当t∈[t0,T)时, 有 (15) 由(13)式和(15)式可知 (16) 及 定理3的证明对任意序列tn→∞, 令Un=U(x,y,tn;U0). 由于自反巴拿赫空间的有界序列都是弱紧的, 所以存在一个序列{Un}和函数U, 使得 令测试函数 (17) 对(17)式等号左边第二项用分部积分法, 结合ρ(0)=ρ(1)=0, 令δ=t-tn, 得 (18) ‖U(tn+δ)-ωδ‖Lp+1(Ω×{0})→0 ‖U(tn)-ω‖Lp+1(Ω×{0})→0 下证在Ω×{0}中几乎处处有ωδ=ω. 结合能量等式和Hölder不等式, 当tn→∞时, 有 因为0≤δ≤1, 当tn→∞时, 有‖U(tn+δ)-U(tn)‖L2(Ω×{0})→0, 即在Ω×{0}中几乎处处有ωδ=ω. 重新整理(18)式, 可得 (19) 由勒贝格控制收敛定理可知, 当tn→∞时, (19)式后3项趋近于0. 对第二项, 有 故U(tn)在弱意义上趋近于一个稳定解.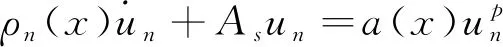
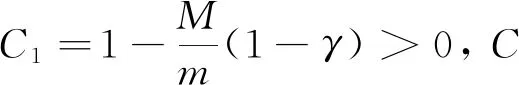
2 渐近行为