一类具有线性和非线性耦合项的Kirchhoff型方程组的基态解①

李振辉，许丽萍

河南科技大学 数学与统计学院， 洛阳 471023

本文研究如下一类Kirchhoff型方程组：

(1)

其中Ω是RN中的光滑区域，N≤3，V(x)是位势函数，ai，bi，λi，μi(i=1，2)是正数，k，β是耦合项系数． 为了研究方程组(1)解的存在性， 假定位势函数V(x)连续且满足如下条件：

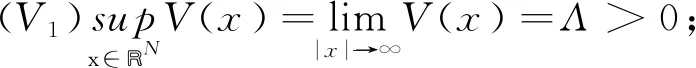
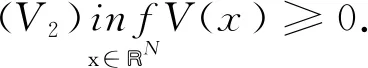
方程组(1)中u和v表示位移，bi是初始张力， 而ai与弹性弦的固有性质有关[1]． 如果V≡0， 那么方程组(1)变为

(2)

如果v≡0，k=0，β=0， 那么方程组(2)可以化简为如下Kirchhoff型方程：

(3)

方程(3)是文献[2]首次提出的， 用来描述弹性弦的自由振荡问题． 随后， 文献[3]用变分法研究了Kirchhoff型方程， 很多学者也对此产生兴趣， 获得了一些重要成果[4-7]． 对于不含非局部项的相关结果可参见文献[8-10]．

(4)

文献[11]用Nehari流形证明了方程组(4)基态解的存在性．k=0时的一些成果见文献[12-16]．

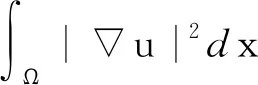
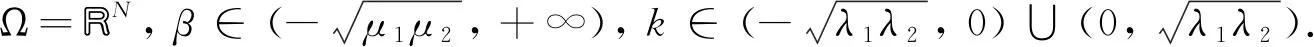
1 预备知识

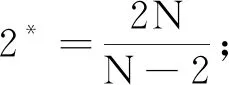
(5)

和范数

(6)

2 定理1的证明

若Ω=RN， 设

H=H1(RN)×H1(RN)

定义H上的内积如(5)式， 范数如(6)式． 对∀(u，v)∈H， 设方程组(2)的能量泛函为

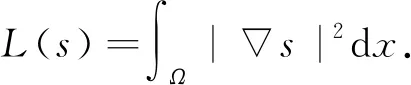
令

N={(u，v)∈H {(0， 0)}： J(u，v)=0}

易知， 方程组(2)的非平凡解(u，v)∈N． 下面先证明方程组(2)存在一个半平凡解， 从而可得N≠∅．

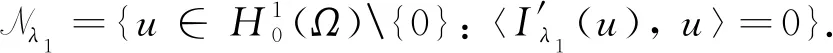
如果Ω=RN，a1=1，b1=0， 则方程(3)可以简化为

-Δu+λ1u=μ1u3u>0，u∈H1(RN)

(7)

注1若|Ω|<∞， 由引理1知方程组(2)存在一个半平凡解； 若Ω=RN， 由引理2知方程组(2)存在一个半平凡解． 无论哪种情形， 方程组(2)都存在一个半平凡解， 于是得到N≠∅．

引理3N是H的一个光滑子流形．

证对∀(u，v)∈N，

(8)

易见， 引理3成立．

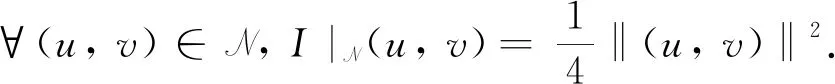
证若(u，v)∈N， 那么

J(u，v)=0

(9)

即

因此， 对∀(u，v)∈N，

由Sobolev嵌入定理得

既然‖(u，v)‖≠0， 那么存在C1>0， 使得对∀(u，v)∈N， ‖(u，v)‖≥C1>0．

引理5若(u，v)是I|N的临界点， 那么(u，v)也是I的临界点．

证若(u，v)是I|N的临界点， 那么I′(u，v)=ηJ′(u，v)， 其中η∈R是一个Lagrange乘子． 于是

〈I′(u，v)， (u，v)〉=η〈J′(u，v)， (u，v)〉

由(8)式和(9)式得η=0． 引理5成立．

引理6若{(un，vn)}⊆H是I|N的PS序列， 那么{(un，vn)}是I的PS序列． 而且， 若Ω有界， 那么存在(u，v)∈N， 使得{(un，vn)}在H上有一个收敛于(u，v) 的子列．

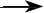
I|′N(un，vn)=I′(un，vn)-ηnJ′(un，vn)

那么

o(1)=〈I′(un，vn)， (un，vn)〉-ηn〈J′(un，vn)， (un，vn)〉=-ηn〈J′(un，vn)， (un，vn)〉

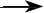
I′(un，vn)=ηnJ′(un，vn)+o(1)=o(1)

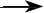
设

(10)

(11)

(12)

若Ω有界， 由Sobolev紧嵌入定理，c1和c2是存在的． 或者若Ω=RN， 由集中紧性原理可得c1和c2是存在的． 由引理4得

(13)

定理1的证明由c>0和文献[11]的引理2.2， 存在某个序列{(un，vn)}⊆N， 使得{(un，vn)}是I|N的(PS)c序列． 因此， 由引理6得{(un，vn)}是I的(PS)c序列． 根据对Ω的假定， 拟分两种情形讨论方程组(2)解的存在性．

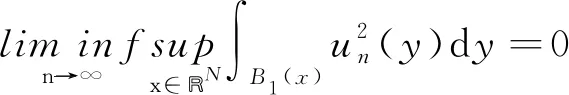
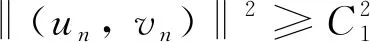
(14)

由引理4有

故有I(u，v)=c． 综上所述， 在两种情形下都有(u，v)∈N，I(u，v)=c，I′(u，v)=0． 因此，u≠0 和v≠0． 接下来， 讨论k取不同范围值时，u和v的符号．

首先， 设k<0． 则

由J(u，v)=0得

对t≥0， 定义一个C1函数φ(t)=I(t|u|，t|v|)， 即

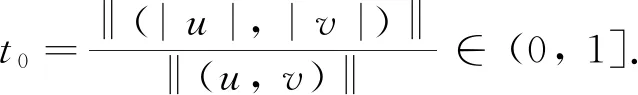
(15)

因此， ‖(|u|， |v|)‖2=‖(u，v)‖2， (|u|， |v|)∈N，I(|u|， |v|)=c． 不失一般性， 可假设u≥0，v≥0． 由引理5知， (u，v)是I的一个临界点． 因此(u，v)是方程组(2)的一个基态解．

由椭圆正则性定理知， ‖u‖L∞<+∞， ‖v‖L∞<+∞． 由于(u，v)是方程组(2)的解， 即

那么， 由最大值原理知

u>0v>0

(16)

再者， 设k>0． 由上述类似的讨论， 易知‖(|u|，-|v|)‖2=‖(u，v)‖2， (|u|，-|v|)∈N，I(|u|，-|v|)=c． 因此， 不妨设u≥0 和v≤0． 由引理6知， (u，v)是I的一个临界点． 因此， (u，v)是方程组(2)的一个基态解． 与(16)式的证明类似， 由椭圆正则原理和最大值原理得u>0，v<0．

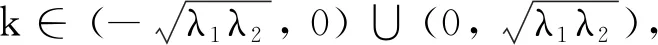
证由注1知， 存在u1>0和v1>0， 使得(u1， 0)，(0，v1)∈N，c1=I(u1， 0)，c2=I(0，v1)． 因此

设g(t，s)=J(tu1，tsv1)． 显然

g(1， 0)=J(u， 0)= 0

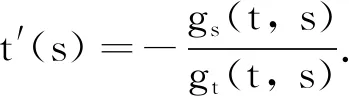
t′(s)=α(1+o(1))t(s)=1+αs(1+o(1))

t2(s)=1+2αs(1+o(1))

因此， 对∀s∈(-s0，s0)， 有

3 定理2的证明

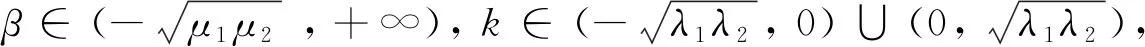
方程组(1)的极限情形是

(17)

设方程组(1)的能量泛函为

类似地， 定义方程组(17)的能量泛函为

设

定义Nehari流形

NV={(u，v)∈H1(RN)×H1(RN){(0， 0)}： JV(u，v)=0}≠∅

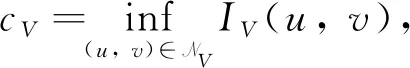
引理7假定V(x)满足条件(V1)-(V2)， 那么cV

Γ={γ∈C([0， 1]，X)：γ(0)=(0， 0)，IV(γ(1))<0}

故有cV

接下来， 我们将用集中紧性原理和引理7证明定理2．