永磁同步电机高速带速重投冲击抑制研究

石运卓,高宏洋,吕雁文

(中车大连电力牵引研发中心有限公司,辽宁 大连116052)

0 引 言

永磁同步电机相比于异步电机具有体积小、重量轻、效率高、结构简单、过载能力强、功率密度大等优点，近年来在各个领域应用日益广泛。

永磁同步电机在运行中，在逆变器脉冲电压断电——恢复的过程中，永磁同步电机进入带速重投工况。由永磁同步电机的稳定运行条件和转子反电势影响，在带速重投过程中会产生较大的电流冲击，这会对主电路器件造成潜在危害。这种现象在随着电机速度的升高而越发明显，因此需要对带速重投冲击现象进行分析和抑制，最大限度的减小带速重投过程中的电流冲击，抑制电机转矩波动，维持控制系统稳定性，保证电气系统的安全性。

1 带速重投电流冲击原理分析

1.1 电机运行稳定条件分析

本文针对永磁体内嵌式永磁同步电机进行研究，其d轴电感Ld与q轴电感Lq不相等。永磁同步电机的极限圆表达式如式(1)所示。

(1)

式中ωr为电机转子角频率，ψf为转子磁链，Usmax为逆变器输出最大电压，Imax为电机最大电流，is为电机输出电流，id、iq分别为d、q轴电流。

随着电机转速升高，电压极限圆收缩，并且逐渐脱离原点。电压极限圆和电流极限圆的关系如图1所示：

图1中，电压极限圆N1、N2、N3、N4、N5所对应的转子角频率分别为ω1、ω2、ω3、ω4，ω5，且ω1<ω2<ω3<ω4<ω5，N0为电流极限圆。

如果电机在角频率大于ω3时进行带速重投操作，此时电压极限圆已经脱离原点。永磁同步电机稳定运行的前提条件是电机的电流矢量顶点处于电压极限圆和电流极限圆的公共区域[1]。

根据永磁同步电机控制系统中电流调节器原理，其输入量为id、iq，输出量是d、q轴电压ud、uq。而一般的电流调节器的输出量无法实现阶跃变化，因此ud、uq无法快速达到期望值，需要经历一个过渡的过程。在电机内部，在其输入端施加电压后，由电机内部的电压电流关系，电机电流也会经历从0开始增加并逐渐过渡到给定电流值的过程[2]，图2表示电机内部电流矢量的过渡过程。在此过程中，电流矢量会处于电压极限圆与电流极限圆公共区域之外。

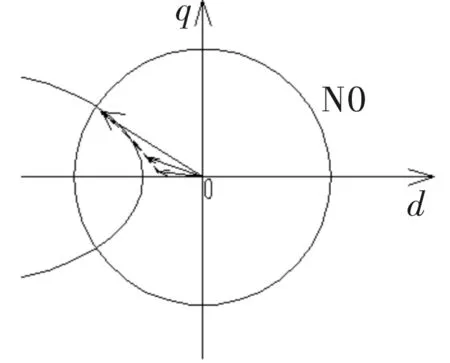
图2 带速重投时电流矢量建立过程

因此由电流调节器和电机内部电压电流关系的综合作用，电机电流无法直接达到期望值，需要经历一个过渡过程。在此过程中，电机的电流矢量会处于电压极限圆与电流极限圆的公共区域之外，由于不满足电机的稳定运行条件，会产生很大的电流冲击[3]。

1.2 转子反电势及脉冲零矢量分析

永磁同步电机在d、q轴坐标系下的电压方程如式(2)所示[4]。

(2)

在式(2)中，e0=ωrψf，该项为永磁电机转子反电势的表达式，Rs为定子电阻。随着电机转速的升高，ωr增加，转子的反电势也会逐渐增大。

当永磁同步电机处于断电运行状态时，逆变器上、下桥臂的脉冲均被封锁，电机定子侧无电压脉冲输入，电机的d、q轴电流为均0，根据式(2)可得：

(ud=0
uq=e0=ωrψf)

(3)

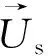
(4)

反电势的存在使永磁同步电机为准发电机状态，由2.1节分析，电流调节器的特性决定其输出电压无法快速达到期望值，因此在带速重投过程中逆变器输出电压与反电势在一定时间内存在幅值差[5]。

如图3所示，传统的SVPWM电压脉冲为七段式结构，由零矢量t0、t7和有效空间电压矢量(本图中为t2、t3、t4)构成，以此来保证在不同空间矢量电压过渡过程中功率器件开关状态变化最小，保证器件损耗最低[6]。

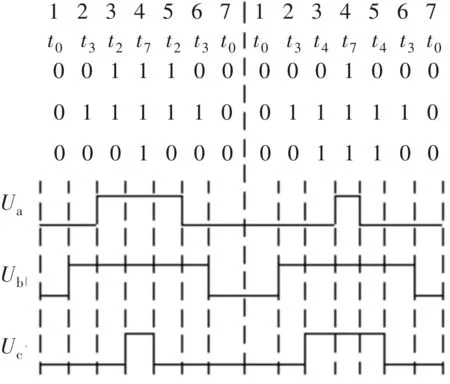
图3 七段式脉冲构成

可见在传统的七段式SVPWM电压脉冲两端，存在零矢量000。由逆变器主电路拓扑，000矢量使逆变器下桥臂的IGBT开通，并和反并联二极管组成三相电流回路。在带速重投过程中，伴随着脉冲零矢量的发出，永磁同步电机的定子端被短路，永磁电机内部产生短路冲击电流。短路电流冲击在电机任何转速下的带速重投过程都会产生，冲击电流的大小与电机转速和零矢量的作用时间有关。一般情况下，电流调节器输出都是从0开始，因此在电压脉冲开始输出时刻，零矢量的占空比最大。

图4为在000矢量作用下，某一转速下永磁同步电机的电流状态。

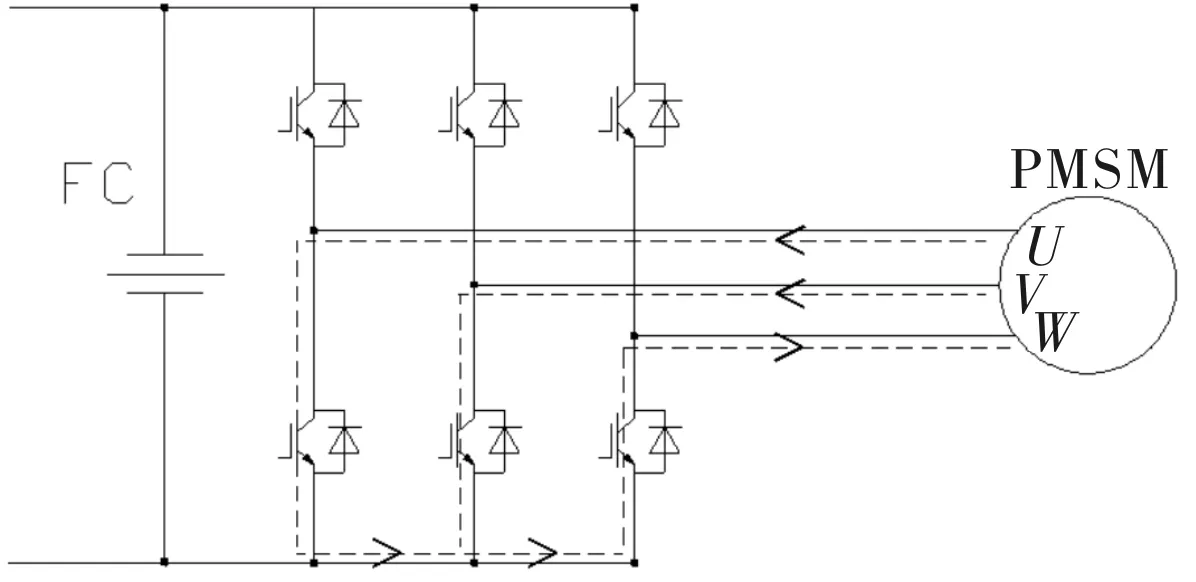
图4 零矢量时电机电流状态

2 高速下电机带速重投电流冲击抑制方式

由第1节的分析，电机在高速运行时引起带速重投冲击的原因有两个：(1)电流矢量处于电压极限圆和电流极限圆的非公共区域；(2)SVPWM电压脉冲中的零矢量引起的电机定子短路。因此可以针对这两个问题分析解决。

2.1 最小d轴电流预给定

由前文分析可知，在电机进行带速重投过程中，需要电机的d、q轴电流快速进入电压极限圆和电流极限圆的公共区域，以保证电机处于稳定工作的条件。d、q轴电流由电机输入电压ud、uq产生，因此电机输入电压需要迅速达到期望值，减小电流矢量的过渡时间。

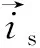
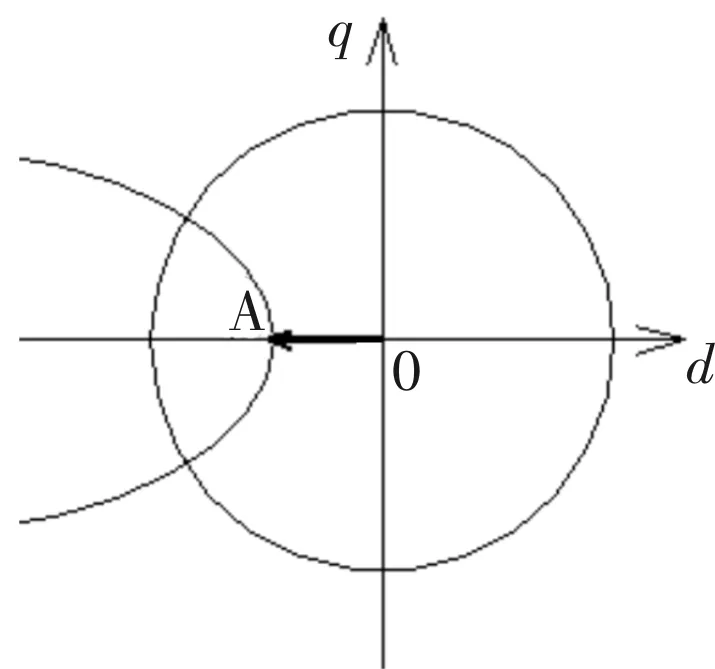
图5 稳定运行时最小电流矢量

可知当电流矢量处于A点时，|id|=|is|，iq=0，因此电流矢量处于A点可以使电机稳定运行且输出转矩为0。

(5)

在计算出预加载电流后，还需保证电流调节器的输出的快速性，使电机电流从PWM脉冲加载时刻起能够迅速达到给定。

永磁同步电机的电流调节器由PI调节器和前馈解耦项组成[8]。其中PI调节器的结构导致正常进行PI调节时其输出无法呈阶跃增长。根据永磁同步电机的解耦规则，可以把电流预给定值加入解耦项，此时电流调节器的输出如式(6)所示。

(6)

由上述分析，再经过简化可得：

(7)

当电机带速重投过程结束且能够稳定运行后，控制器的输入开始向期望值过渡，即在图(6)中从A点过渡到B点，Te为恒转矩曲线。这个过程由控制软件自行调节。

图6 电流矢量过渡过程

2.2 优化SVPWM脉冲调制方式

在施加端电压后，电机内部建立对应的去磁电流仍需要时间，因此在初始电流矢量顶点到达A点的过程中，电机转子反电势仍会大于逆变器的输出电压。由1.2分析，逆变器输出第一个脉冲电压时，由于电机反电势大于输入电压，两者之间存在一个电压差，此时电机处于发电机的状态。则在电压脉冲的零矢量区域，会造成电机定子短路从而造成电流冲击。为了避免施加首个脉冲时出现电机定子短路电流的现象，需要对PWM脉冲进行优化。

根据PWM脉冲等效原理[9]，可以考虑转移零矢量的位置，由图3所示，每一个PWM脉冲都包含有000和111零矢量，零矢量不产生有效电压，仅用来实现两个有效矢量之间的切换。因此在一个PWM电压脉冲中，改变零矢量的位置，不会对电压脉冲的等效值产生影响。

可以考虑把每个PWM脉冲两端的零矢量移至中间，因此七段式PWM脉冲变为五段式PWM脉冲。相比于七段式调制，五段式调制方式在每个载波周期中，只插入单一的零矢量，本文中只保留111零矢量。五段式调制本质上也是基于SVPWM原理，只是在电压波形构建上与七段式调制有所不同[10]。

图7给出了基于五段式由110-010、010-011两个合成矢量的三相电压，其余区间的空间电压矢量合成规则与此类似。

图7 电流矢量过渡过程

五段式占空比的计算方式：

(tx=mTpwmsin(60°-θ)/sin(120°)
tx+1=mTpwmsin(θ)/sin(120°)
t0=Tpwm-tx-tx+1)

(8)

式中，tx和tx+1为相邻矢量作用时间，m为调制系数，Tpwm为调制周期，θ为合成电压矢量与矢量tx的夹角。

由图7可以看出，将零矢量移到脉冲中间后，在脉冲生成时刻，输出到电机端的电压不再经历零矢量作用过程，直接对电机施加期望值电压，避免了短路电流的产生。

3 试 验

依托某永磁同步电机工程项目搭建电机实验平台，对此方法进行验证。牵引电机额定功率120 kW，额定电压555 V，额定电流170 A，额定转矩763 Nm，极对数4，Ld=1.447 mH，Lq=0.6904 mH。牵引逆变器额定电压750 V，额定功率150 kW，最大电流360 A，控制电压24 V。

图8 电机控制实验台

图9为电机在3000 r/min下，采用未进行任何处理直接强制带速重投时的电流波形，可见电机定子电流存在较大的冲击。

图9 3000 r/min下，直接重投时U、V相电流波形

图10为电机在3000 r/min下，采用电流预给定的方式进行带速重投，从波形可见，冲击电流明显减小，残留的定子电流冲击是由脉冲零矢量所引起。

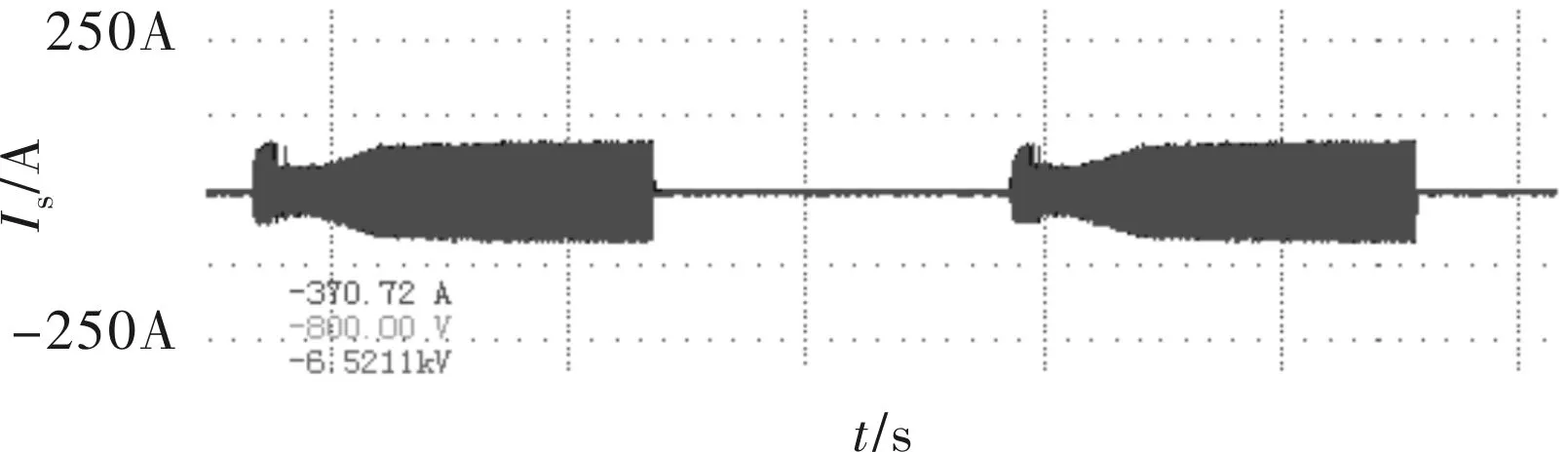
图10 3000 r/min下，采用电流预给定方式的带速重投时U、V相电流波形

图11为采用优化五段式PWM脉冲调制后，3000 r/min时带速重投时的定子电流波形，可见此时电流的冲击已经完全消失。

图11 3000 r/min下，消除零矢量影响后的带速重投时U、V相电流波形

4 结 论

本文针对永磁同步电机高速运行时带速重投过程中电流冲击问题的根源进行了分析，采用了d轴电流预给定方式和优化PWM脉冲调制的方式进行优化，这样即能保证电机内部电流矢量快速进入稳定区域，又能防止产生短路电流，从而对带速重投过程中的冲击电流加以有效抑制。

实验表明，本文提出的带速重投电流冲击抑制方法，可以有效的对带速重投过程中所产生的冲击电流进行抑制，使带速重投过程中的冲击电流基本消除，提升了电机运行的稳定性。并且本方法易于实现，符合实际工程项目应用要求，适用范围广泛。