平面高速冲压机构的摆动力完全平衡设计与计算

聂亚彪， 沈惠平， 杨廷力

(常州大学 现代机构学研究中心， 江苏 常州 213164)

未经平衡的机构存在周期变化的摆动力和摆动力矩，会引起机械振动和噪声，并影响工作精度，因此，消除或减小机构惯性力，实现摆动力和摆动力矩的平衡，是高速机构设计中不容忽视的问题[1-2]。

目前，连杆机构摆动力完全平衡的3种主要研究方法是线性独立矢量法[3-4]、质量替代法[5](质量静替代、质量动替代、广义质量替代)、附加杆组法[6]。其中，线性独立矢量法可实现一般平面机构的摆动力平衡，但由于其推导过程过于繁琐，一定程度上限制了该方法的应用；质量替代法会加大机构本身质量和构件本身摆动力矩，增加构件内部动应力；附加杆组法是对机构附加其他杆组实现摆动力完全平衡的方法，但不具有一般性。

BERKOF等[7]提出线性独立向量法，它利用机构的矢量闭环方程，得到一组线性无关的向量，并消去矢量方程中有关时间参数，最终得到摆动力完全平衡方程。YE等[8]将构件质量看成是“可流动”的“质量流”，当机构所有构件的质量都流到机架上时，该机构就实现了摆动力完全平衡。OUYANG等[9-10]提出一种调整机构运动学参数(AKP)的方法，实现其摆动力完全平衡的目的。文献[11-12]通过优化机构总质心加速度值，使平面串联机械手的摆动力明显下降。

文献[13-15]提出了质量矩替代法，其基本思想是：将连枝杆件的质量矩，通过与其相连的移动副或转动副，转化到与其相邻的树枝杆件上，从而将复杂平面机构的动平衡问题，转化为树系统中全部树枝构件的动平衡问题；且给出了含有一个和两个连枝构件回路的质量矩替代公式，以及一杆多副树枝构件的质量矩求解公式，由这些质量矩替代公式，可以构造出平面机构中全部树枝构件摆动力完全平衡计算的条件。该方法的优点有：①相比于质量替代法，无需引入较复杂的广义质量概念以及替代点选择问题；②相比于线性独立矢量法，它无需推导复杂的位置方程；③相比于附加杆组法，无需附加杆组而占据大量空间。因此，质量矩替代法是一种优秀的摆动力完全平衡方法，它可使机构摆动力完全平衡条件的建立过程大大简化，具有物理意义清晰、求解过程简单、计算量小、普遍性好等优点，尤其适合于具有解析式位置正解的平面和空间机构。

文章主要从3个方面进行研究：①通过拓扑降耦的方法，设计得到了一种零耦合度的、具有解析式位置正解及输入-输出部分运动解耦性的两滑块高速冲压机构，这种高速冲压机构具有自动防护功能，即主滑块用于冲压，副滑块用于自动辅助推料器；②将“质量矩替代法”应用于具有工业应用背景的、多回路平面机构(含3个子运动链-SKC)的摆动力完全平衡设计与计算，为该两滑块高速冲压机的研发奠定技术基础；③验证质量矩替代法在应用于具有解析式位置正解、多回路平面机构摆动力完全平衡设计与计算时所具有的上述优势。

1 冲压机构的拓扑优化设计及分析

文献[16]所述的一种具有两个滑块的平面八杆冲压机构，如图1(a)所示，该机构为平面Ⅲ级机构，位置正解求解比较复杂，且不具有位置解析解。根据机构降耦设计方法[17]，将机构中的运动副B，运动副C合并，即可将原机构的耦合度从1变为0，从而使得改进机构具有正向位置解析解，改进设计后的机构简图，如图1(b)所示。

图1 一种两滑块高速冲压机构的优化Fig.1 Optimization of a high speed stamping mechanism with two sliders

由图1(b)可知，改进设计后的高速冲压机构主要由机架0，构件1～构件7组成，其中，杆组(构件4～构件6)(构件1～构件3)(构件2～构件7)为3个平面Ⅱ级杆组。移动副P1(主滑块)为主冲压头，移动副P2(副滑块)为辅助推料器，其余7个关节(A～G)均为转动副。该机构的拓扑分析为：

1)自由度分析

该机构包含3个独立回路，即E-D-F，C-B-A，B-G-P2，每个回路的独立位移方程数ξLi=3(i=1，2，3)，全周自由度公式为[18]

因此，机构仅需要一个原动件，例如，可取杆5为驱动曲柄，当冲压机头P1向下冲压时，辅助推料器P2完成自左向右的冲压料自动推送，从而完成自动冲压。这样，避免了人工送料，具有很好的防护功能，保证了操作人员人身安全。

2)耦合度计算

E-D-F，C-B-A，B-G-P23个回路的约束度分别为：

因此，机构的耦合度为

由上可知，改进后的机构包括3个子运动链(SKC)，即SKC1，SKC2，SKC3，耦合度均为0。因此，机构的耦合度为0，其位置正解具有解析解，为接下来的该机构动平衡和动力学计算提供了极大方便。

2 机构摆动力完全平衡计算

2.1 质量矩替代法基本概念及求解步骤

整个机构可看成是由树枝构件和连枝构件组成的完整树系统。连枝构件是指连接两个支链与机架，或者连接两个独立的开链的构件。将整个机构中所有的连枝构件的质量矩，都由与之相邻的树枝构件的附加质量矩替代后，此时，机构中所有回路拆解成只含有树枝构件组成的支链，再将各个支链的质量矩加起来，即可得到整个机构的质量矩。连枝构件的存在，使得计算多回路机构的总质量矩，转化为求解各个支链中树枝构件的总质量矩。该冲压机构包含3个基本回路，因此，含有3个连枝构件。除连枝构件外，其他都为树枝构件。机构摆动力完全平衡条件的求解步骤见文献[14]。

2.2 摆动力完全平衡条件求解

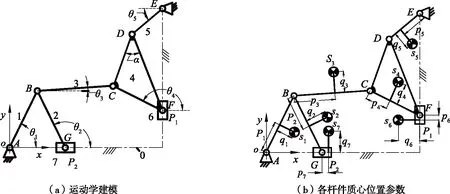
图2 坐标系建立及参数标注Fig.2 Setting up coordinate system and parameter marking

2.2.1 可完全平衡判定以及树系统划分

由图2可知，该机构中每一构件都存在一条仅由转动副组成的通路连接到机架，即可判定该机构可用配重法实现摆动力完全平衡。

树系统划分：根据2.1节所述的连枝构件、树枝构件选取原则，选取构件3，构件6，构件7为连枝构件，构件1，构件2，构件4，构件5为树枝构件。

2.2.2 连枝构件质量矩的附加质量矩替代

1)连枝构件3

由图1(b)可知，连枝构件3左边通过复合铰链RB，分别与树枝构件1、树枝构件2联接；其右边通过转动副RC与多副构件4联接，因此，其质量矩替代过程如下。

连枝构件3的质心(S3)位置表示为

(1)

由图2易得以下运动学关系：

(2)

(3)

(4)

(5)

将式(3)、式(4)、式(5)，代入式(2)得：

(6)

(7)

由式(6)、式(7)可知，连枝构件3的质心参数可由杆件1、杆件4或杆件2、杆件4上的坐标参数表示。因此，连枝构件3的质量矩可表示为：

(8)

(9)

(10)

(11)

(12)

由式(8)、式(9)可知，连枝构件3的质量矩可由其相邻树枝构件1和相邻树枝构件4，或树枝构件2和树枝构件4的附加质量矩替代，并且附加质量矩表达式不包含连枝构件3的位置参数θ3。也因此可知，对于含有复合铰链的机构，在保证机构总质量矩不变的前提下，连枝构件的质量矩替代可有多种选择方案。

2)连枝构件6

由图2可知，连枝构件6通过转动副RF与多副树枝构件4相连。因此，其质量矩替代过程为：

连枝构件6的质心(S6)位置表示为

(13)

由图1(b)可知，有运动学关系

(14)

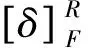
连枝构件6的质量矩为

(15)

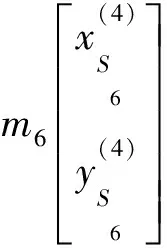
将式(13)、式(14)代入式(15)可知，连枝构件6的质量矩可由作用在树枝构件4上的附加质量矩替代，并且附加质量矩表达式不包含连枝构件6的位移参数。

3)连枝构件7

类比于连枝构件6的质量矩替代公式，易得到连枝构件7的质量矩，可由作用在连枝构件2上的附加质量矩替代，并且附加质量矩表达式中，不含有连枝构件7的位移参数为

(16)

2.2.3 建立全部树枝构件的摆动力完全平衡条件

1)树枝构件4

树枝构件4分别通过转动副RF和转动副RC，与连枝构件6和连枝构件3相连，故树枝构件4受到的质量矩分别有：

①连枝构件3、连枝构件6分别作用在树枝构件4上的附加附加质量矩，分别见式(12)、式(15)；

②树枝构件4本身及其配重的质量矩分别为：

(17)

(18)

同时，由式(12)、式(15)、式(17)、式(18)，可知，树枝构件4的总质量矩为

(19)

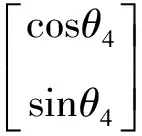
(20)

2)树枝构件5

由图2可知，树枝构件5并没有直接与连枝构件相连，但树枝构件5通过转动副RD与连枝构件4联接，其中，树枝构件4相当于树枝构件5的子树系统，故树枝构件5受到的质量矩分别有：

①连枝构件3作用在树枝构件5上的附加质量矩为

(21)

②连枝构件6作用在树枝构件5上的附加质量矩为

(22)

③树枝构件4及其配重对树枝构件5的附加质量矩

(23)

④树枝构件5及其配重质量矩，分别为：

(24)

(25)

同时，由式(21)～式(25)可知，树枝构件5的总质量矩为

(26)

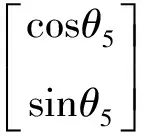
(27)

3)树枝构件2

由图2所示，树枝构件2分别与连枝构件3、连枝构件7通过RB,RG直接相连，故树枝构件2受到的质量矩分别有：

①连枝构件7作用在树枝构件2上的附加质量矩，见式(16)；

②树枝构件2及其配重质量的质量矩，见式(28)、式(29)；

(28)

(29)

同时，由式(16)、式(28)、式(29)，树枝构件2的总质量矩为

(30)

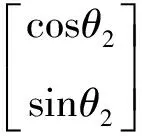
(31)

4)树枝构件1

由图2可知，树枝构件1通过复合铰链RB与连枝构件3、树枝构件2联接，其中，树枝构件2相当于树枝构件1的子树系统树，故树枝构件1受到的质量矩作用，见式(32)～式(37)。

①连枝构件7作用在树枝构件1上的附加质量矩为

(32)

②连枝构件3作用在树枝构件1的附加质量矩，见式(10)；

③树枝构件2及其配重对树枝构件1的附加质量矩为

(33)

④树枝构件1本身及其配重质量矩为：

(34)

(35)

同时，由式(10)、式(32)～式(35)可知，树枝构件1的总质量矩为

(36)

(37)

2.2.4 数值求解

为简化模型，设冲压机构中各根杆件质量均匀分布，具体参数为：

1)各杆件长度

l1=l2=109 mm，l3=170 mm，l4=80 mm，l5=117 mm，l6=80 mm，l7=40 mm。

2)各杆件质心位置参数

3)各杆件质量及配重质量

4)其他参数

多副杆4为等腰直角三角形，α=45°；驱动构件5作匀速转动，输入角速度为w1=0.1π rad/s。

因连枝构件的质量矩已经被相邻构件附加质量矩替代，故对于连枝构件无需添加配重。

将上述数值参数分别代入式(20)、式(27)、式(31)、式(37)，可分别求得树枝构件4、树枝构件5、树枝构件2、树枝构件1附加配重参数为：

(38)

(39)

(40)

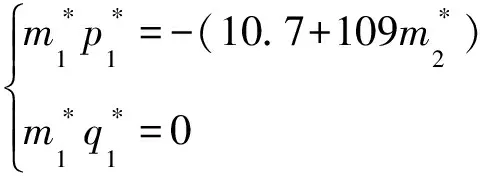
(41)

3 平衡前后机构总质心、总惯性力对比分析

为验证冲压机构动平衡效果——总质心静止不动或总质心位移变化缓慢，给出平衡前后机构总质心、总惯性力对比分析。

3.1 平衡前总质心位移变化以及总惯性力求解

改进设计后的冲压机构的位置正解，可转化为3个SKC各自位置正解的求解。

1)SKC1的求解

由E点的坐标E(m,n)，易知D点，F点坐标分别为：D(m-l7cosθ5，n-l7sinθ5)；F(m，Dy+

l5sin(θ4-α))。

2)SKC2的求解

易知C点、B点的坐标分别为：C(Dx-l4sinθ4，Dy+l4cosθ4)；B(l1cosθ1,l1sinθ1)。

3)SKC3的求解

易知G点、A点的坐标分别为：G(Bx-l2cosθ2,0)；A(0,0)。

于是，可求出各个杆件的质心坐标分别为：

(42)

(43)

(44)

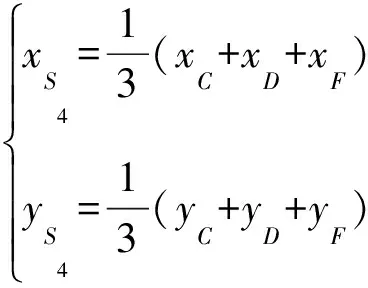
(45)

(46)

(47)

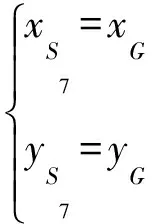
(48)

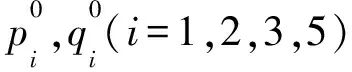
因上述各构件的质心位置均为解析解，其加速度计算十分容易。由式(42)～式(48)易得机构平衡前总质心变化，如图3(a)、图3(b)、图3(c)中实线所示。总惯性力在横、纵坐标方向的变化，如图4(a)、图4(b)中实线所示。

图3 机构平衡前后总质心坐标及轨迹变化Fig.3 The change of total center of mass coordinates and track before and after mechanism balancing

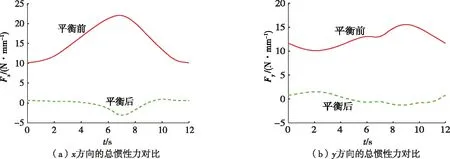
图4 机构平衡前后的机构惯性力Fig.4 Inertia force of mechanism before and after balancing

3.2 平衡后总质心位移变化以及总惯性力求解

(49)

式中pi，qi(i=1,2,4,5)为构件1、构件2、构件4、构件5加配重后新的质心位置参数。

基于式(49)，可求得加配重之后，各树枝构件新的质心坐标为：

(50)

(51)

(52)

(53)

将式(50)～式(53)与平衡前的连枝构件质心方程(44)、方程(47)、方程(48)一起，计算出加速度后，由Matlab计算，可分别得到平衡后机构总质心变化轨迹，如图3(a)、图3(b)、图3(c)虚线所示。总惯性力在横、纵坐标方向的变化，如图4(a)、图4(b)中虚线所示。

3.3 平衡前后总质心位移及总惯性力对比变化

由图3(a)、图3(b)可以看出，平衡前，机构总质心在x，y方向都有较大的位移波动，特别是在纵坐标方向上；平衡后，机构总质心位移波动已很小。由图3(c)可以看出，平衡前后质心轨迹变化较大，平衡前质心轨迹所围成的面域，要远远大于平衡之后。因此，平衡后机构在x，y方向上的位移均有明显的减小。同时，平衡后的质心位置更接近机架的同时，面域更小，几乎接近于0，表明平衡后质心位置更加稳定。

由图4可以看出，平衡前，机构在x，y方向的总惯性力都有较大波动，加以适当的配重参数后，在同样的转速运动下，机构x，y方向总惯性力都几乎接近于0。因此，平衡后的总惯性力波动也较小，基本达到了摆动力完全平衡，从而也验证了基于质量矩替代法的摆动力完全平衡计算的正确性，为该两滑块高速冲压机的研发奠定了理论依据。

4 结 论

1)将质量矩替代法推广应用于含多副杆件、多个复杂SKC平面八杆冲压机构的动平衡设计与计算，通过拓扑降耦，使其耦合度降为0。该机构具有解析式位置正解，无需通过一维搜索，即可精确求解各构件的位置及加速度值，为机构的动平衡计算分析提供了极大方便。

2)用质量矩替代法导出了高速冲压机构的摆动力平衡设计与计算公式，计算得到其平衡配重质量的位置参数。计算表明：平衡后总质心位置变化范围很小，x，y方向的总惯性力几乎为0，高速冲压机构较好地实现了摆动力平衡效果，证明了该方法的有效性。