重视过程教学培养学生数学学科的核心素养

傅晓

摘要： 史宁中先生在一次讲座中曾指出数学教学要培养学生的数学学科的核心素养.具体对教学的要求可以理解为“三会”：学生会用数学的眼光观察现实世界（抽象）、学生会用数学的思维思考现实世界（推理）、学生会用数学的语言表达现实世界（模型）.在图形与几何板块教学过程中教师可以通过设计一系列探究活动，培养学生的数学学科的核心素养.

关键词： 过程教学;探究活动;数学学科核心素养

过程教育是指在满足学生全面、和谐发展的需要，关注数学结果的形成、应用的过程和获得数学之后的反思过程的育人活动. 在数学教学中，如何设计有效的数学活动，帮助学生积累数学活动经验从而提高学生的数学素养是当下数学教育者研讨的焦点.笔者以浙教版八年级上册1.5《三角形全等的判定（2）》探究活动设计和教学实践为例阐述核心素养背景下几何教学过程中探究活动的设计与思考.

1 课堂探究活动设计呈现

探究活动（一）

把两根塑料棒一端用螺栓固定，转动塑料棒，沿塑料棒内侧，在透明纸上画出∠A.

①取AB=10cm，AC=6cm画出△ABC.

②将你画的三角形与同伴所画的三角形进行比较，它们能互相重合吗？你有什么发现？

③若固定两塑料棒之间的夹角为30°，在透明纸上画出△ABC. 将你画的三角形与同伴所画的三角形再进行比较，你又有什么发现？

探究活动（二）

①已知△ABC，AB=5cm， AC=3cm，∠B=30°，畫出△ABC. 与你的同伴交流，你有什么发现？

②∠B=30°，AB，AC满足什么条件△ABC能确定.

2 探究活动设计的思考

2.1探索“SAS”定理，关注数学结果的形成

探究活动（一）设计说明：在前一节课中学生已经经历：两边确定-固定第三边-确定三角形-SSS的学习过程.本节课在学生已有的认知起点上继续设计探究活动探索新知.把两根塑料棒的一端用螺栓固定，学生经历转动塑料棒，沿塑料棒内侧，在透明纸上画出∠A.通过这样画角的实践活动，感受数学的抽象.第一次让学生自主探索并感受、发现“仅有两边，无法确定一个三角形”;取AB=10cm，AC=6cm画△ABC所画三角形与同伴所画三角形对比，第二次感受因夹角∠A的不同，发现所画三角形是不全等的;接着当三角形两边长度固定，取AB=10cm，AC=6cm，再固定三角形两边的夹角30°，对比后，第三次经历并发现：当三角形的两边和夹角确定的时候，所画三角形形状和大小是确定的.以上数学活动设计给与学生足够的时间和空间经历实验、观察、猜想，激发了学生的学习兴趣，培养学生良好的数学学习习惯，使学生掌握恰当的图形与几何数学学习方法.

“SAS定理”的教学设计是数学新知研究的基本套路，它可以对今后探索平行四边形的性质和判定、特殊平行四边形的性质和判定产生正迁移. 此类新知习得的过程可以说是模型化过程，体现数数学具有应用的广泛性. 就如章建跃博士提出的“基本套路”是培养学生发现和提出问题、分析和解决问题的能力的落脚点.课堂教学过程中需要教师重视此类过程学习的基本套路，从而培养学生的数学学科素养.

2.2“SSA”的探索，关注数学结果的反思

探究活动（二）设计意图：本探索过程的设计，通过画图使得学生感悟到满足“已知两边及一边的对角”条件的三角形是不确定.因此“已知两边及一边的对角”（简称“边边角”）不能作为判定两个三角形三角形全等的条件.在教学过程中利用这一典型的反例来帮助学生理解：“SSA”这一命题是假命题.

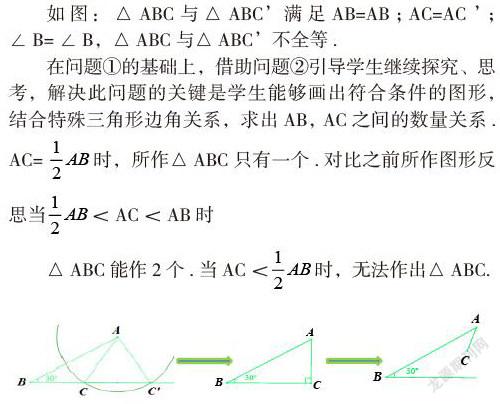
如图：△ABC与△ABC’ 满足AB=AB;AC=AC ’;∠B=∠B，△ABC与△ABC’不全等.

在问题①的基础上，借助问题②引导学生继续探究、思考，解决此问题的关键是学生能够画出符合条件的图形，结合特殊三角形边角关系，求出AB， AC之间的数量关系. AC=时，所作△ABC只有一个.对比之前所作图形反思当

△ABC能作2个.当AC<时，无法作出△ABC.

本环节的探究过程可以帮助学生借助图形理解全等三角形概念和三角形全等的判定定理，提高学生的画图能力，问题的探索过程经历抽象到直观，拓展学生的思维深度.

结束语：

数学素养是通过数学知识的学习过程建立起来的素养，数学知识的学习过程是发展素养的基本途径与内容，核心素养的培养应该渗透数学学习的整个过程. 只有设计适切的探究活动使学生经历数学活动后才能获得数学经验，才有可能将做一件事情获得的经验迁移到做另一件事情上，提高学习能力、继而发展素养.

参考文献：

[1]全日制义务教育数学课程标准[S].北京师范大学出版社，2001

[2]邬云德.基于过程教育的“一次函数应用（第2课时）”课例及分析[J].中学数学（初中版），2015（10）

[3]许芬英.浙江省中小学学科教学建议案例解读（初中数学）[S].浙江教育出版社，2015（7）.