某空气涡轮起动机转子系统动力学特性分析

周煌亮，臧朝平

(南京航空航天大学，江苏 南京 210016)

0 引言

大功率齿轮箱装置是空气涡轮起动机的重要组件之一[1]，涡轮转子通过行星齿轮系统将动力输出。在研究起动机转子系统的振动特性时，通常只考虑涡轮转子本身及其轴承支承系统而忽略与其相连接的齿轮系统，或者单独研究行星齿轮减速器的动态特性。由于转子与齿轮系统联接耦合在一起，齿轮系统的振动会对转子的临界转速及振动响应产生影响。因此，分析研究转子-齿轮系统动力学特性，实现空气涡轮起动机转子-齿轮系统的动态设计是非常重要的[2-5]。

本文将齿轮啮合简化为弹簧连接，采用石川模型计算得到齿轮形变量及啮合刚度的平均值，然后基于Ansys经典界面，建立了涡轮转子-齿轮系统简化有限元模型，对涡轮转子-齿轮系统进行了临界转速特性分析以及不平衡响应分析[6]。

1 建立计算模型

1.1 结构介绍

涡轮起动机转子系统主要包括两部分，第一部分为单涡轮转子，第二部分为齿轮系统。行星齿轮本身偏心质量较小，其本身产生的不平衡载荷可以忽略，齿轮啮合可认为是一种特殊支承。由于只考虑横向振动自由度，齿轮的支承刚度可通过齿轮啮合刚度在轴心方向的投影得到。因此，本文在求解结构的临界转速时，将齿轮的啮合简化为弹簧连接处理，起动机的转子系统可简化为如图1所示。

图1 转子系统结构简化示意图

1.2 齿轮啮合刚度计算

当一对轮齿在分度圆节点上均匀接触时，把每单位齿宽的齿面法向载荷和每个轮齿齿面法向变形量和的比值定义为一对轮齿的刚度K，其数学表达式为

(1)

其中：Fn为作用与齿廓的法向力；b为齿宽；δ为轮齿的总变形量。为了简化计算，齿轮变形量的计算通常采用当量齿形法。

目前，工程中常用当量齿形模型为石川模型。由该模型可知，轮齿的总体变形应包括当量齿形中矩形和梯形的弯曲和剪切变形、轮齿基体弹性倾斜引起的轮缘变形以及轮齿的接触变形等。

根据材料力学相关方法，轮齿矩形部分产生的弯曲变形δBr可表示为

(2)

式中：Fn为作用在轮齿上的法向载荷；E为齿轮材料的弹性模量；hx为轮齿啮合点的高度；hr为轮齿当量齿形矩形部分的高度；SF为轮齿当量齿形矩形部分的厚度；βx为法向载荷的作用角。

轮齿梯形部分产生的弯曲变形δBt为

(3)

轮齿总剪切变形δS为

(4)

式中υ为泊松比。

基体弹性倾斜引起的轮齿变形δG为

(5)

此外，轮齿接触变形δPv为

(6)

轮齿在载荷作用点的总变形量为

δ=δBr+δBt+δS+δG+δpv

(7)

当作用于齿轮上的载荷为单位载荷时，即可求解轮齿的柔度，进而求得齿轮副啮合刚度。齿轮副的综合啮合刚度是指轴截面内齿轮总刚度的平均值。由于重合度影响，齿轮副啮合刚度以齿轮基节为周期变化。根据定义，齿轮的综合啮合刚度为该周期内的平均值。

1.3 计算模型

空气涡轮起动机转子系统主要包括涡轮转子和行星齿轮系统两部分，基于Ansys建立了涡轮转子-齿轮系统有限元模型如图2所示。双联齿轮简化为集中质量，采用Ansys中的mass 21单元模拟。齿轮啮合简化为弹簧连接，连接刚度由平均啮合刚度沿轴心方向的投影得到。采用Combin14单元模拟，Combin14单元是两节点二维单元，且无弯曲以及扭转状态。

图2 涡轮转子-齿轮系统耦合有限元模型

2 动力学求解及分析

2.1 涡轮转子-齿轮系统的临界转速分析

采用坎贝尔图法对转子系统的动力学特性进行分析，主要考虑起动机转子系统72 000r/min内的临界转速特性，得到转子系统的坎贝尔图如图3所示。

图3 涡轮转子的坎贝尔图

由图3可知涡轮转子-齿轮系统在到达最转速72 000r/min的过程中有两阶临界转速如表1所示，两阶临界振型分别如图4和如图5所示。

表1 涡轮转子-齿轮系统临界转速对比

图4 涡轮转子的第一阶临界振型

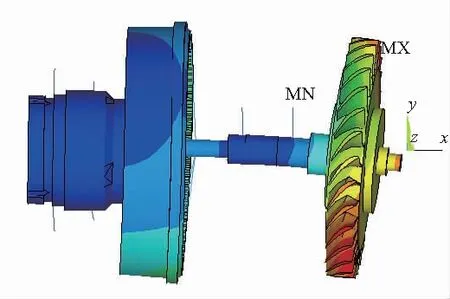
图5 涡轮转子的第二阶临界振型

第一阶临界振型主要为转子系统的偏摆振动，最大振动位置出现在内齿圈轮毂上；第二阶临界振型也为转子系统的偏摆振动，最大振动位置出现在涡轮转子上。

2.2 涡轮转子-齿轮系统的不平衡响应分析

假设转子系统在涡轮盘处存在10g·mm的不平衡量，进行稳态动力响应计算，分析频域范围0～1 000Hz，包含了转子系统工作转速区域(0～900Hz)。得到涡轮转子叶尖、涡轮转子轴端和内齿圈处稳态响应曲线如图6所示，各不同位置响应值对比如表2所示。

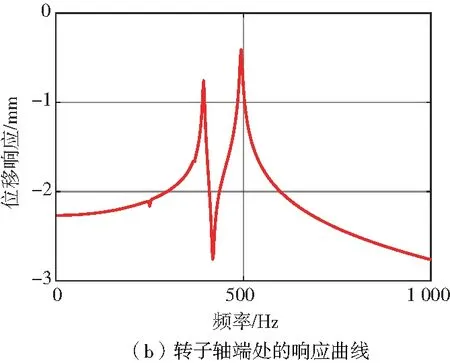
图6 涡轮转子-齿轮系统各位置响应曲线

表2 涡轮转子-齿轮系统不同位置处响应值

由图6可知，不平衡响应计算得到的转子系统前两阶临界转速为394Hz、494Hz，与坎贝尔图计算得到的临界转速基本吻合。

由图6以及表2可知，在转子系统一阶临界转速附近(394Hz)，转子轴端处响应值最小，涡轮盘以及内齿圈处响应较大。这是由于转子一阶振型是涡轮盘以及内齿圈的局部振动为主，其中涡轮盘处的响应为内齿圈处响应的24%。

在转子二阶临界转速494Hz处，涡轮盘以及内齿圈处响应较大，这是由于转子二阶振型是涡轮盘以及内齿圈的局部振动为主，其中涡轮盘处的响应与内齿圈处响应相当，二者比例为84%。

3 结语

本文研究的是某型空气涡轮起动机的涡轮转子-齿轮系统的动力学特性，首先基于石川模型计算了齿轮副的形变量以及平均啮合刚度，在将齿轮啮合简化为弹簧连接的简化原则下，建立了涡轮转子-齿轮系统有限元模型。基于Ansys对涡轮转子-齿轮系统进行了临界转速分析以及不平衡响应分析，分析结果表明：

1)在起动机上升到最高转速的过程中，存在两阶临界转速分别为23 821r/min以及31 332r/min。两阶临界振型都为内齿圈以及涡轮转子的偏摆振动。

2)在转子一阶临界转速附近，内齿圈处振动响应值最大，为3.030mm，转子轴端以及涡轮盘处振动响应值较小，分别为0.175mm以及0.737mm。

3)在转子二阶临界转速附近，内齿圈处以及涡轮盘处的振动响应值较大，分别为1.78mm以及1.50mm，转子轴端处振动响应值最小，为0.39mm。