一种高增益软开关直流变换器的分析与设计

胡宇婷，谌 思，罗全明

（输配电装备及系统安全与新技术国家重点实验室（重庆大学），重庆 400044）

随着光伏产业的不断发展，对其系统内部能量变换的研究越来越受到重视。在一般的采用两级式发电系统中包括两级功率变换单元，分别是前级DC/DC 直流变换单元以及后级DC/AC 逆变单元[1-3]。前级直流变换单元连接的光伏电池单元与直流母线，其中光伏电池单元输出电压较低，而直流母线电压较高。传统的升压电路如Boost 变换器已不能满足该应用场合对光伏电池输出低压到直流母线高压变换的需求[4-10]。因此，研究者们对可以实现高增益变换的变换器进行研究，提出了大量的高增益变换器。

文献[11]提出了Boost 级联型变换器，该变换器增益为级联单元增益的乘积，拓扑中开关均工作于硬开关状态，开关过程损耗较大，后级电路开关直接承受母线电压，电压应力较高，因此该拓扑更适用于中小功率应用等级；文献[12]提出带有有源箝位的耦合电感型拓扑，有效抑制电压尖峰的产生，但耦合电感设计较为复杂，为得到更高的增益其体积也较大；文献[13]提出了一种带倍压单元的升压拓扑，该拓扑通过电容与二极管的组合使变换器增益实现倍增，且开关电压应力降低为传统拓扑的一半，虽然存在部分开关的硬开关问题，该倍压组合依旧是相对简单高效的提高增益的方式。

本文基于硬开关问题的解决思路以及倍压单元的引入，提出一种高效率、高增益直流变换器。首先对其进行拓扑推演、工作原理分析以及性能特点分析，最后通过实验验证该拓扑的性能。

1 拓扑推演

为得到高增益升压电路，现对传统Boost 升压电路进行分析。图1 为传统同步整流Boost 变换器电路，开关管S1和S2为互补导通。为针对硬开关问题提出解决方案，对其开关过程进行进一步分析。开关管S1关断后，电感电流通过S2体二极管续流，此时施加驱动信号则可以实现S2的零电压开通。而当开关管S2关断时，电感电流无法通过S1的体二极管续流，因此S1工作于硬开关状态。

图1 传统同步整流Boost 变换器Fig.1 Conventional synchronous rectified Boost converter

为了实现开关管S1的软开关，可以在开关管S1、S2与电感L 的公共点A 处，添加一条辅助电流支路ia，使得电感电流有机会由S1体二极管续流，辅助支路添加示意如图2 所示。

辅助支路的构成如图2（b）所示。图2（b）为S1软开关的具体实现方案：在S2断开、S1尚未开通之前，辅助电流ia和电感电流iL之差对开关管S1寄生电容放电、充电。当电容放电完毕时，S1体二极管导通，此时S1两端电压近似为0，则S1实现零电压开通。

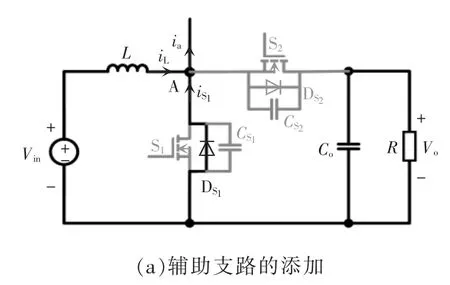
图2 辅助支路添加示意Fig.2 Schematic of adding auxiliary branch

将上述软开关思路以及文献[13]里的倍压单元与升压整流电路进行组合，即得到本文所提高增益软开关直流变换器。该拓扑的组成如图3 所示，其中软开关单元的电容与倍压单元的电容合并为图3 中的电容C1。

图3 单向高增益软开关直流变换器Fig.3 Single-direction high-gain soft-switching DC/DC converter

2 工作原理

本文提出的高增益DC/DC 变换器中，同步整流单元包括电感L、同步整流开关S1和S2；软开关单元包括辅助实现软开关的电感La和C1；倍压单元包括电容C1和C2及二极管D1和D2。详细分析在一个开关周期内变换器的9 个开关模态，各开关模态的等效电路及主要波形分别如图4 和图5 所示。图4 中标识了电流的实际方向，其中各元件电流参考方向如图3 所示，电压与电流的参考方向一致。

图5 在一个开关周期内的工作波形Fig.5 Operation waveforms during one switching period

（1）开关模态1[t0～t1]：如图4（a）所示，在t0时刻之前，开关S1导通、S2关断，辅助电感电流流经二极管D1，La承受的电压小于0，电流不断减小，在t0时刻减小至0。因此，在t0时刻由0开始负向线性增大，流经二极管D1的电流换向至二极管D2。L 两端的电压为Vin，iL线性增大。至t1时刻，开关S1断开，模态1 结束。模态1 的方程为

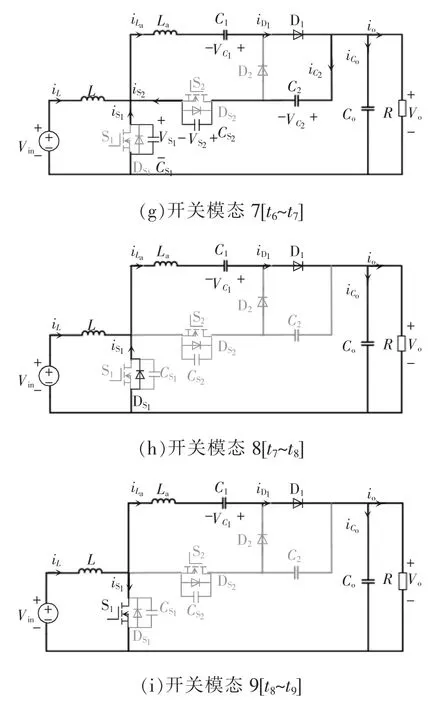
图4 各开关模态等效电路Fig.4 Equivalent circuit in each switching mode

（2）开关模态2[t1～t2]：如图4（b）所示，在t1时刻，开关管S1关断，外部电流对充电、放电，直至t2时刻两端电压上升至两端电压下降至0，即分别完成充放电，此工作模态结束。由于此模态过程短暂，因此可认为电感电流变化斜率在此模态中近似不变。

（3）开关模态3[t2～t3]：如图4（c）所示，由于在上一时刻两端电压下降至0，t2时刻S2体二极管开始导通。此时由于二极管导通，S2两端近似为零电压，此时施加驱动信号于S2即可实现其零电压开通。在该模态中，L 两端的电压为Vin+-Vo，iL开始线性下降；La两端电压为由负值线性下降。t3时刻，开关管S2导通，变换器进入下一个工作模态。

（4）开关模态4[t3～t4]：如图4（d）所示，t3时刻S2零电压开通，其电流大小为iL与之和，方向与参考方向相反，iL与保持上一模态的斜率线性变化。在t4时刻，从负向减小至0，二极管D2实现了零电流关断，至此模态4 结束。模态4 的方程为

（5）开关模态5[t4～t5]：如图4（e）所示，在t4时刻，二极管D2关断、D1导通，同时La中的电流改变方向。输入电感L 的端电压保持不变，iL继续线性下降；辅助电感La的端电压变为，电流由0 开始线性上升。流经开关管S2的电流即和iL之差开始由负值逐渐减小，至t5时刻电流下降至0，模态5 结束。模态5 的方程为

（6）开关模态6[t5～t6]：如图4（f）所示，在t5时刻，开关管S2中的电流改变方向，从0 开始正向增长。各开关管与二极管导通关断状态与上一工作模态一致，各电感电流的变化斜率不变。至t6时刻，开关管S2关断，变换器进入下一工作模态。

（7）开关模态7[t6～t7]：如图4（g）所示，在t6时刻，开关管S2关断，外部电流对电容放电、充电。至t7时刻S1端电压下降至0，S2端电压上升至Vo-，此工作模态结束。由于此工作模态时间很短，可近似认为电感电流变化斜率在此工作模态中不变。

（8）开关模态8[t7～t8]：如图4（h）所示，由于S1两端电压在前一模态下降至0，t7时刻S1体二极管开始导通。在此工作模态中，输入电感L 两端电压变为Vin，iL开始线性上升；辅助电感La的端电压变为开始正向线性减小。至t8时刻，开关管S1驱动导通，此工作模态结束。

（9）开关模态9[t8～t9]：如图4（i）所示，由于保持导通，开关S1两端电压近似为0，t8时刻S1零电压导通。此模态中电感电流变化斜率不变。至t9时刻，电流减小为0，二极管D1零电流关断，此工作模态结束，同时变换器结束了一个开关周期，即将进入下一个开关周期。模态9 的方程为

3 性能分析

进一步分析上述高增益软开关直流变换器的性能，主要包括电压增益、半导体元件电压应力和软开关工作条件。

3.1 电压增益

由于死区时间很短，为了简化性能分析过程，现将死区时间忽略不计，变换器的主要工作波形如图6 所示。

图6 中：d1为辅助电感La电流从正向峰值减小归零的时间间隔，d2为从负向峰值减小归零的时间间隔，D 为占空比，Ts为开关周期。

图6 变换器主要工作波形Fig.6 Main operation waveforms of the converter

由变换器的工作模态分析，并且根据输入电感L 的伏秒平衡原理，可以得到

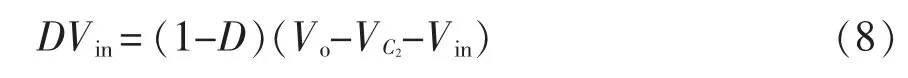
同理，根据辅助电感La的伏秒平衡原理，可以得到

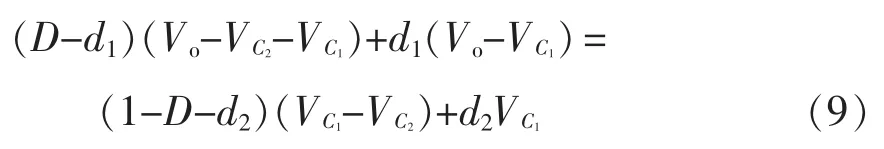
由式（8）和式（9）可以得到

将式（10）代入式（11），可得

根据图6 中辅助电感La的电压和电流，可知La的电流峰值为

由工作模态分析可知，稳态时，二极管D1和D2在一个开关周期内的电流平均值等于负载电流，即

将式（14）代入式（16），可以得到

将式（10）和式（12）代入式（17），可得电压增益为

式中，R 为负载。令Δd=d1-d2，由于占空比D≫Δd，因此式（18）可简化为

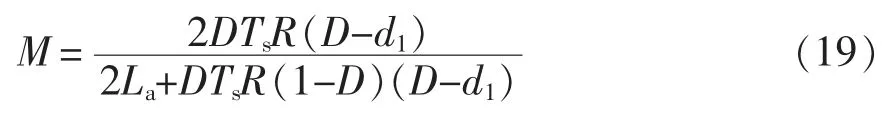
联立式（13）和式（15）解得

将式（12）代入式（20），可以得到

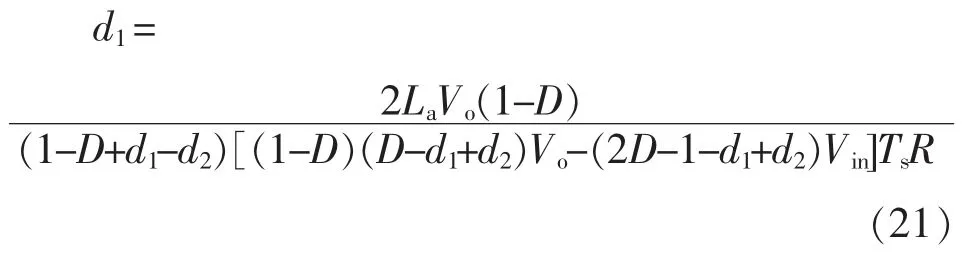
由于占空比D>>Δd，且M=Vo/Vin，因此式（21）也可表示为

同理可得

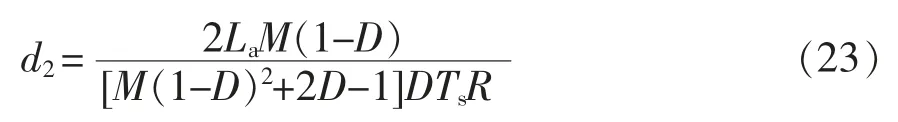
将式（23）代入式（19），可以得到

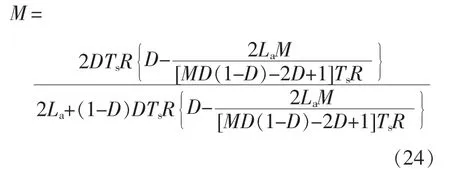
化简式（24）可得

由式（26）可以看出，该变换器的电压增益的大小取决于占空比D、辅助电感La、开关周期Ts以及负载R。

当2La=α 时，式（26）可化简为

由上述分析可知，在不影响变换器正常工作的前提下，通过合理设计辅助电感La，本文所构建拓扑的电压增益可近似达到基本Boost 变换器电压增益的2 倍。

3.2 电压应力

由变换器工作模态分析可以得到开关管S1、S2的电压应力为

二极管D1和D2的电压应力可以表示为

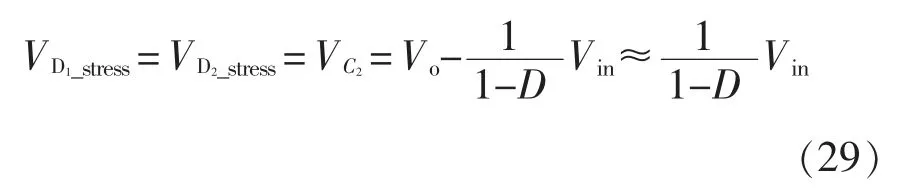
由式（28）、式（29）可知，开关管S1、S2的电压应力和二极管D1、D2的电压应力均等于Vin/（1-D），相比于传统Boost 变换器，当输出电压相同时，本文所提出的拓扑其电压应力约为传统Boost 变换器开关器件电压应力的一半。因此可选择额定电压较低的开关器件，从而降低开关损耗，减小元件体积，提高变换器转换效率。

3.3 软开管工作条件

传统旅游消费形式将因80后、90后成为消费主力的更替和收入水平的不断提高而发生巨大的变化。未来一定时期内广大游客对旅游目的地产品的质量和服务要求越来越高，对旅游的舒适度和品质化要求也会进一步凸显。旅游者的不同国度、不同文化背景、不同消费动机等等，都使中高端游将成为新时代旅游消费的突出特征，为此，建构高质量的旅游产品和服务体系，培养个性化服务人才是新时代我国旅游专业人才培养的必然要求。

在t6时刻，开关管S2关断，变换器进入死区时间。电流iL和电流之差对开关管S1的并联寄生电容放电，同时对开关管S2的并联寄生电容充电。因此要实现开关管S1零电压导通，须满足辅助电感La和输入电感L 的能量之差大于并联寄生电容完成充放电所需要的能量，从而使得在开关管S1导通之前，其上反并联寄生二极管处于续流导通状态，则有

且在t8时刻，电流iL和电流之差仍须满足iL（t8）-≤0 才能保证在续流过程结束之前，开关管驱动导通，避免并联寄生电容再次充电使其无法实现零电压导通。

由式（30）可知，当辅助电感La很小或者输入电感L 很大，亦或电路轻载时，都可能无法满足开关管S1实现零电压导通的条件，因此增大辅助电感La或者减小输入电感L 均有助于开关管S1实现零电压导通。

3.4 损耗分析

电力电子变换器的损耗主要分为功率变换部分损耗和控制部分损耗，其中功率变换部分损耗占主要部分。其中功率部分损耗主要为各电路元件的损耗，在本文提出的变换器中具体表现为开关管损耗、二极管损耗及磁性元件损耗。由于该变换器开关管均实现零电压开通，所以开关管损耗仅计算导通损耗及关断损耗。开关管S1导通损耗与关断损耗分别为

同理可得开关管S2导通损耗与关断损耗分别为0.71 W 与1 W。由于变换器中二极管实现了零电流开通关断，所以仅计算二极管导通损耗PD_con，计算公式为

磁性元件La损耗主要包括磁芯损耗（铁损）和绕组损耗（铜损），其峰值磁通计算为

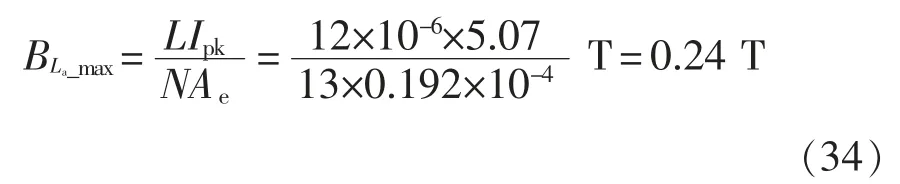
查阅磁芯材料手册可得该峰值磁通对应的磁芯比损耗为30 mW/cm3，可得La的铁损与铜损分别为

同理可得L1的铁损与铜损分别为0.12 W 与5.20 W。估算得高增益软开关变换器总损耗为17.36 W，同理可计算出添加辅助电感La前变换器各部分损耗。

图7 为添加辅助电感前与添加辅助电感后损耗分布。其中，有辅助电感La电路即为本文提出的高增益软开关直流变换器，无辅助电感La电路即为Boost 同步整流与倍压电路组合所得高增益直流变换器。可以看出，添加辅助电感后由于S1实现零电压开通使开关管损耗降低，添加的辅助电感使电感总损耗增加。但由于减少的开通损耗比增加的辅助电感损耗多，相比同类型高增益变换器，本文提出的高增益软开关变换器总损耗有所降低。

图7 损耗分布Fig.7 Distribution of loss

4 实验研究

为了验证上述工作原理及性能分析的正确性，搭建了250 W 的实验平台进行实验验证。本文实验参数如表1 所示。

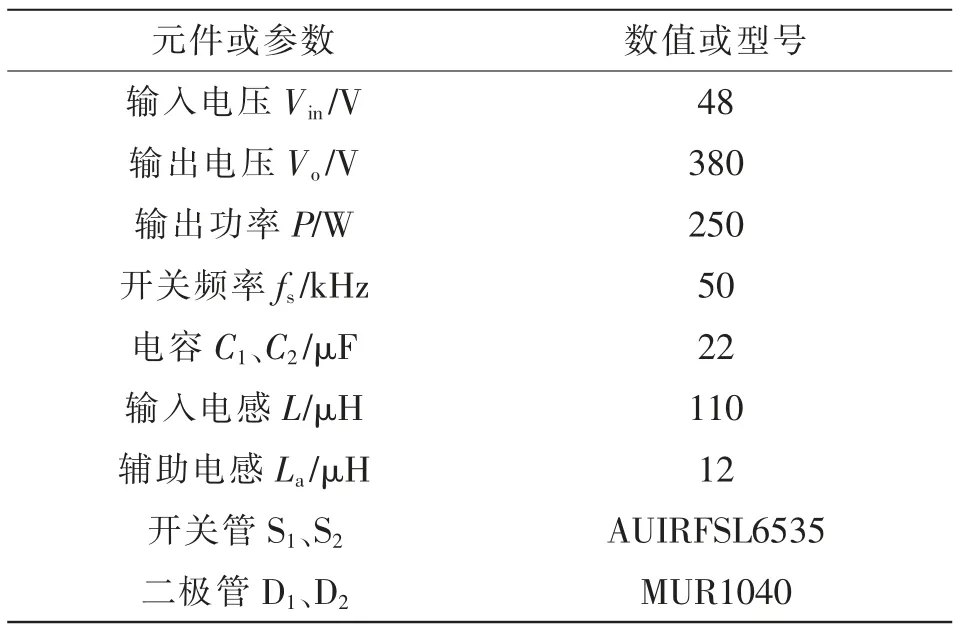
表1 拓扑实验参数Tab.1 Experimental parameters of topology

图8 为主开关管S1驱动信号、输入电压Vin、输出电压Vo以及电容C1、C2电压的实验波形。从图8（a）可以看出，该变换器可实现输入48 V 到输出380 V 转换，并且占空比D 约为0.75；由图8（b）可知，电容电压均在180～190 V之间，约为输出电压Vo的一半，且略大于，与理论分析一致。

图8 开关管S1 驱动、输入电压Vin、输出电压Vo、电容电压和实验波形Fig.8 Experimential waveforms of ,Vin,Vo, and VC

图9 给出了开关管S1的驱动信号、电压以及开关管S2的驱动信号和电压的实验波形。

图9 和及和实验波形Fig.9 Experimential waveforms of ,and

从图9 可以看出，开关管S1和S2在对应驱动信号到来之前，其端电压均先降为0，开关管均实现了零电压开通。开关管S1和S2的电压应力均接近190 V，远小于输出电压，与原Boost 变换器相比，在输出电压相同的条件下，该变换器开关管的电压应力得到了显著降低，与理论分析一致。

图10 为变换器二极管D1、D2的电压实验波形。从图10 中可以看出，这2 个二极管的电压应力约为185 V，约为输出电压的一半，与原Boost变换器相比，当输出电压相同时，二极管的电压应力明显降低，与理论分析一致。

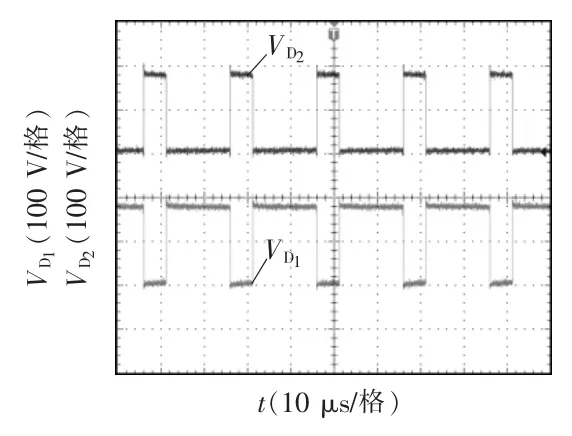
图10 二极管D1、D2 电压实验波形Fig.10 Experimential waveforms of and

图11 给出了在输入电压为48 V、输出电压为380 V 不变，输出功率Po在50～250 W 之间变化时所提变换器的效率曲线。从图11 中可以得出，在输出功率为150 W 时，变换器达到其最大效率92.48%；满载时其效率约为92%，与前述估算所得损耗分析结果一致。

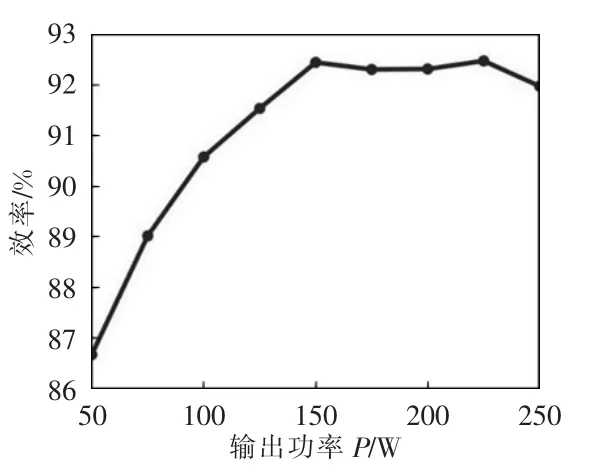
图11 效率曲线Fig.11 Efficiency curve

5 结论

本文从传统同步整流电路出发，针对开关管硬开关的问题提出了解决方案，并结合倍压电路单元提出了一种新型高增益软开关直流变换器，并对该变换器进行了拓扑推演、工作原理阐述、性能分析。实验结论如下：

（1）在48～380 V 的转换中，占空比有效控制在非极限占空比范围内；

（2）开关管均实现了零电压开通，有利于降低开关损耗，提高变换效率；

（3）半导体器件电压应力均约为输出电压的一半，有利于选择导通电阻较小的器件，减少导通损耗。