一种应用于光伏并网发电系统的新型双输入DC-DC 变换器

李洪珠，刘飞扬，李洪璠

（1.辽宁工程技术大学电气与控制工程学院，葫芦岛 125105；2.三亚学院理工学院，三亚 572022）

随着光伏发电、燃料电池等新型能源在并网发电系统中的广泛应用，高增益DC-DC 变换器成为电力电子领域的研究热点之一[1-2]。在光伏并网发电系统中需要将多个光伏电源并联在公共母线上，供给并网逆变器等直流负载使用；使用传统单输入直流变换器，其结构较为复杂且成本较高。采用多输入变换器代替多个单输入直流变换器可以简化电路，减低成本。因此国内外对应用于多输入DC-DC变换器进行了大量研究，并取得了较多成果[3-6]。

文献[7]提出了一种新型双输入变换器，可以实现输入电源的灵活切换，但其开关管较多；文献[8]提出了一种新型双输入Buck-Boost 直流变换器，但其电压增益较低；文献[9]提出了一种基于倍压单元的双输入变换器，简化了变换器结构，但其二极管数量较多。在变换器中应用变压器或耦合电感是目前研究的热点之一[10-11]。耦合电感高增益变换器具有电路结构简单，通过增加耦合电感匝比可以大幅度提高变换器电压增益的优点[12-13]。

通过对文献的研究结合耦合电感的优点，本文提出一种具有高增益低电压应力的双输入DC-DC变换器。该拓扑通过控制开关管的关断可以实现输入电源的接入和切除；通过改变耦合电感匝比提高变换器的电压增益，使其具有更宽的电压调节范围；应用三电平结构大幅降低开关管和二极管电压应力。给出变换器主要工作波形和等效电路，分析变换器主要性能。并通过实验验证理论分析的正确性。

1 变换器拓扑及工作模态分析

1.1 变换器拓扑

变换器拓扑如图1 所示，此拓扑由2 个上下对称的耦合电感Boost 变换器组成。一部分在上（电感L1、L2），另一部分在下（电感L3、L4），L1和L2、L3和L4均为正向磁耦合，三电平电容C1、C2串联并联在输出端。为方便分析，假设开关管和二极管为理想器件，忽略C1、C2上电压脉动，变换器工作在电感电流连续状态CCM（continuous conduction mode），不考虑耦合电感漏感的影响。

图1 耦合电感双Boost 拓扑变换器Fig.1 Coupled inductor dual-Boost topology converter

1.2 单输入工作状态分析

当变换器在只有一个输入电源时，其工作模式与带抽头的耦合电感Boost 电路工作原理相同，以Ui1作为单一输入源为例，一个周期共有2 个工作模态，主要工作波形及各模态等效电路如图2 和图3 所示。

图2 单输入模式变换器主要工作波形Fig.2 Main working waveforms of converter in singleinput mode

图3 单输入各模态等效电路Fig.3 Equivalent circuit in each single-input mode

工作模态1[t0～t1]：在t0时刻，开关管S1导通、S2关断；二极管VD1、VD2、VD4关断，VD3导通；电感L1开始储能，电流线性上升；电感L2的同名端电压为正，二极管VD1截止；电感L2、L3、L4中电流为0，电容C1通过二极管VD3为负载提供能量。

工作模式2[t1～t2]：在t1时刻，开关管S1关断、S2关断；二极管VD2、VD4关断；电感L1中的电流开始下降，电感L2的异名端电压为正，二极管VD1、VD3导通；耦合电感L1、L2和电源串联对负载供电，同时对电容C1充电，一直到t2时刻结束，进入下一个周期。

1.3 双输入工作状态分析

在双输入工作状态下，变换器存在开关管交错导通和同时导通与关断2 种工作模式[14]，且2 种模式的电压增益及应力相同。本文的理论分析采用交错导通控制模式，在此模式下，输出电压纹波较小，可以使用较小的滤波电容，减小电容体积。

在实际应用中为了达到所需要的电压增益，占空比D 一般大于0.5，因此本文以D>0.5 进行分析。开关管在交错导通工作模式时，变换器在一个工作周期内共有4 个工作模态，主要工作波形及各模态等效电路如图4 和图5 所示。

图4 双输入模式变换器主要工作波形Fig.4 Main working waveforms of converter in dualinput mode

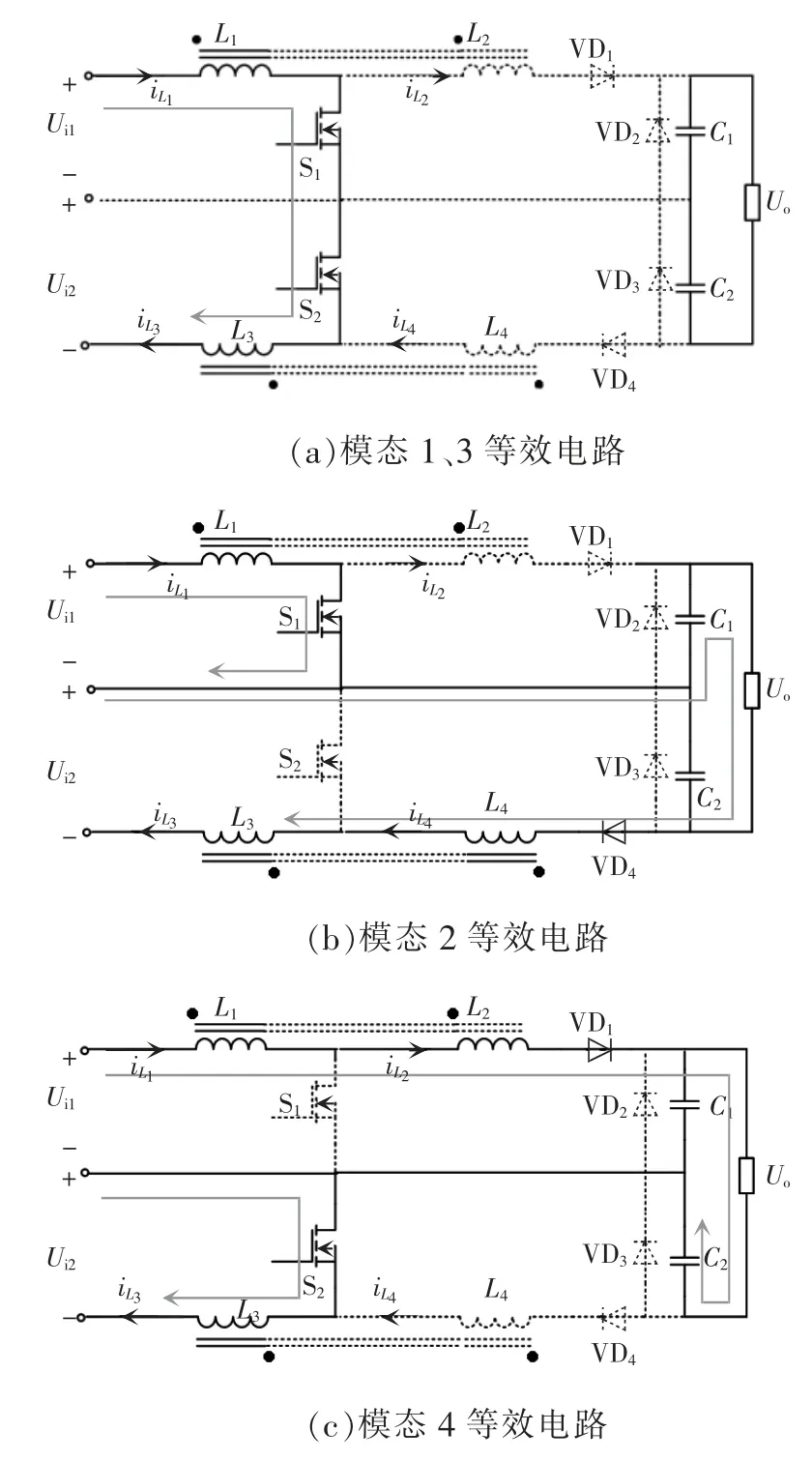
图5 双输入模式各模态等效电路Fig.5 Equivalent circuit in each dual-input mode

工作模态1[t0～t1]：在t0时刻，开关管S1、S2导通，二极管VD1、VD2、VD3、VD4截止；电感L1、L3储能，电流线性上升，一直到t1时刻iL3达到最大值；根据耦合关系，电感L2、L4的同名端电压为正，电感L2、L4中电流为0；电容C1、C2串联为负载提供能量。

工作模态2[t1～t2]：在t1时刻，开关管S1导通，S2关断，二极管VD1、VD2、VD3截止，VD4导通，电感L1中的电流继续上升，电感L2中电流为0；耦合电感L3和L4与电源Ui2和电容C1串联对负载供电，同时为电容C2充电。

工作模态3[t2～t3]：在t2时刻，开关管S1、S2导通，电感L1、L3储能，电流线性上升，一直到t3时刻电感L1电流达到最大值，其等效电路和模态1 相同。

工作模态4[t3～t4]：在t3时刻，开关管S2导通，S1关断，二极管VD2、VD3、VD4截止，VD1导通；电感L4中的电流继续上升，电感L3中电流为0；耦合电感L1和L2与电源Ui1和电容C2串联对负载供电，同时为电容C2充电。一直到t4时刻结束，进入下一个周期。

2 工作性能分析

设L2与L1匝比为N1，L4与L3匝比为N2。

2.1 单输入模式电压增益

以Ui1为单一输入电源为例，在电感L1、L2全耦合情况下，根据磁路定理，电感量和匝数关系为

由于L1和L2为带中心抽头的耦合电感，因此模态2 时存储在电感L1中的能量一部分通过磁耦合关系由电感L2释放，另一部分通过电路连接关系由其自身释放，因此耦合电感可以等效为一个电感Leq1释放能量。推导耦合电感L1、L2的串联等效电感Leq1表达式为

由图2 所示，在开关管导通和关断时刻，电感L1的电流各有一个突变的过程，这个过程是2 个模态切换瞬间等效电感变化造成的。设L1在开关管导通前后时刻的电流分别为，在开关管关断前后时刻的电流分别为，根据电感能量守恒得到

模态1 的电压方程为

模态2 的电压方程为

由式（5）和式（6）可以得到

根据图2 可以得到

由式（3）、式（4）和式（7）、式（8），根据伏秒积原理可以推导得变换器电压增益表达式为

式中，D1为开关管S1的占空比。

同理可得，当Ui2作为单输入电源时，变换器的电压增益表达式为

式中，D2为开关管S2的占空比。

2.2 双输入工作状态电压增益

由图4 和图5 可见，变换器工作在交错导通控制模式下时，L1和L3在储能模态下各自独立，互不影响；在能量释放时，2 个输入电源和各自单元内的电感串联，同时给负载和输出电容供电；因此，电容C1、C2上的电压等于各自对应单元的输出电压。结合式（9）和式（10）得到交错导通模式下变换器电压增益为

由式（11）可以看出随着耦合电感匝数比N 的增大，变换器增益也增大。表1 为3 种双输入升压变换器电压增益对比，相较于传统变换器，本文提出的变换器电压增益较大。

表1 电压增益对比Tab.1 Comparison of voltage gain

2.3 变换器电压应力

2.3.1 单输入电压应力

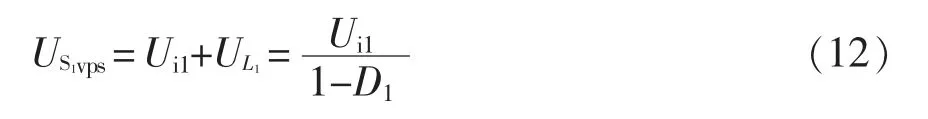
当开关管导通时，二极管截止，二极管D1的电压应力为电感L2端电压和输出电压Uo之和，即

2.3.2 双输入电压应力

根据第2.2 节中的分析可知，双输入时开关管应力与各自单元中的输入电源电压有关，综合式（12）与式（13）可求出双输入时开关管和二极管电压应力，如表2 和表3 所示。对比可知，在双输入模式时虽然输出电压提高，但其开关管和二极管电压应力不变，只与各自单元中的输入电压有关。

表2 二极管电压应力对比Tab.2 Comparison of voltage stress in diode

表3 开关管电压应力对比Tab.3 Comparison of voltage stress in switching tube

3 漏感对电压增益的影响

为了方便分析，以开关管同时导通关断模式为例对漏感进行分析。工作波形及等效电路如图6 所示。根据变压器等效模型，变换器拓扑的等效电路如图6（b）、（c）所示，其中：Lk1、Lk2分别为两耦合电感单元折算后的漏感；Lm1、Lm2为两耦合电感单元励磁电感；分别为两耦合电感单元内电感耦合系数；iN1、iN3为耦合电感原边电流，iN2、iN4为耦合电感副边电流。由于2 个单元具有对称性，因此图6（a）仅给出了、iN1、iN2电流波形。

2 个耦合电感单元内的耦合系数分别为

由图6 可见，其工作方式与第1.2 节相似，因此不再具体描述。考虑漏感分压对变换器电压增益的影响，列写模态电压表达式。

模态1，根据图6（b）电感串联分压，可得励磁电感电压表达式为

模态2，根据图6（c）可以得到

图6 工作波形及等效电路Fig.6 Working waveforms and equivalent circuits

对励磁电感Lm1应用伏秒积平衡定理，可以得到电压增益表达式为

根据第2.2 节分析，可得工作在双输入模式下变换器电压增益表达式为

式（17）和式（18）表明，由于漏感的存在，降低了变换器的电压增益。电压增益随耦合系数K' 变换，设双输入模式时N1=N2=N=2，=K'，不同耦合系数电压增益曲线如图7 所示。随着耦合系数的减小，电压增益减少。

图7 不同耦合系数电压增益曲线Fig.7 Curve of voltage gain with different coupling coefficients

4 实验验证

为验证上述分析，搭建了实验样机，实验测试平台如图8 所示。实验样机参数如下：输入电压Ui1=Ui2=12 V，开关频率f1=f2=50 kHz，开关管交错导通相位差为180°，占空比D1=D2=0.6，电容C1=C2=50 μF，负载电阻R=55 Ω，各耦合电感匝比为1∶1，实际参数如表4 所示。

图8 实验平台Fig.8 Experimental platform

表4 电感实际参数Tab.4 Actual inductance parameters

图9 为开关管驱动波形，2 个开关管占空比均为0.6、相差180°导通。图10 为输出电压波形，输出电压约为95 V，约为输入电压12 V 的8 倍。图11为耦合电感电流波形，由图11（a）可明显地看出电流突变，电感L1和L3，L2和L4电流波形对称，相位差为180°，验证了第1.2 节的理论分析。图12 为开关管和二极管电压应力波形，可见开关管电压应力远小于输出电压。

图9 开关管驱动波形Fig.9 Driving waveform of switching tube

图10 输出电压波形Fig.10 Waveform of output voltage

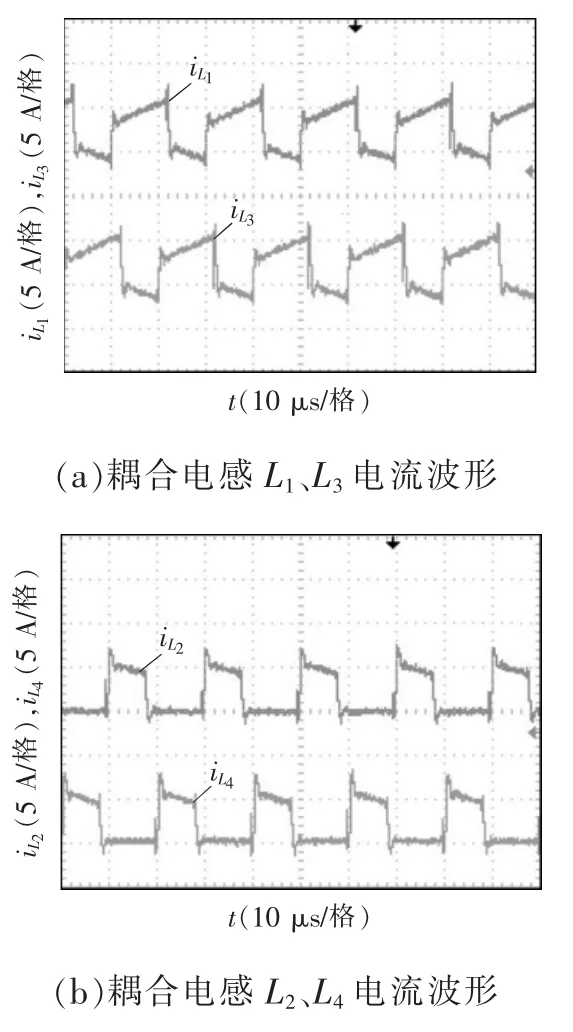
图11 耦合电感电流波形Fig.11 Current waveforms of coupled inductors

图12 开关管与二极管电压波形Fig.12 Voltage waveforms of switching tubes and diodes

输出电压为95 V 不变时，变换器效率曲线如图13 所示。从图13 中可以看到变换器输出功率在80～150 W 变化时，约在130 W 时曲线趋于平稳，变换器效率为93%左右。通过以上实验波形，验证了前述理论分析的正确性。

图13 样机效率曲线Fig.13 Efficiency curve of prototype

5 结论

本文提出了一种基于耦合电感的高增益双输入三电平DC/DC 变换器，分析了变换器的电压增益、开关管和二极管电压应力。通过分析和实验验证，验证了所提变换器具有以下特点：

（1）双输入高增益直流变换器工作时相当于2个直流电源串联供电，同时提高了变换器电压增益，避免了极限占空比的情况。

（2）相较于传统变换器，双输入电源具有单输入和双输入2 种模式为负载供电，提高了电源的利用率和灵活度，简化了变换器结构，降低了成本。

（3）开关管和二极管的电压应力远低于变换器输出电压，使得变换器可以采用内阻较小的器件，减小了器件损耗。

基于上述优点可见，该双输入变换器性能较好，适用于光伏、燃料电池等新能源并网发电。