基于不连续控制的含寄生参数开关变换器的指数稳定性分析

曾海威，杨 汝，胡 维，余连德，杨 红

（1.广州大学物理与电子工程学院，广州 510006；2.广州大学机械与电气工程学院，广州 510006；3.广州大学实验中心，广州 510006）

基于Buck 拓扑结构的DC/DC 变换器由于具有设计简单、成本低等优点，在电子器件、通信设备和汽车系统等工业领域得到了广泛的应用[1-4]。

目前，在DC/DC 变换器的稳定性分析中已取得了许多成果，传统的稳定性分析方法包括小信号分析法、离散模型分析法、Lyapunov 函数分析法、符号序列法、切换系统分析法等[5-10]，上述方法均是基于变换器的近似模型分析DC/DC 变换器的稳定性。Buck 变换器是典型的切换不连续系统，具有强非线性特性，线性化模型并不能完全反映电流连续模式Buck 变换器的动态特性。

本文在分析过程中加入了变换器功率回路的元器件寄生参数，元器件的寄生参数变化会使得变换器系统的稳定性受到影响，在分析变换器稳定性时加入电路寄生参数可有效地提高稳定性分析的可靠性[11-12]，本文提出的分析方法可以分析元器件的寄生参数出现异常增大时使得变换器发生不稳定的现象。本文采用不连续控制的指数稳定分析方法则不须对变换器模型做近似化处理，可完整反映变换器的特征。

基于脉冲宽度调制PWM（pulse width modulation）型的DC/DC 开关变换器的控制通常有双线性理论控制[13]、滑模控制[14]、自适应控制[15]、鲁棒控制[16]等控制方法。这些控制方法虽然具有非线性的性质，但是仅仅确保了系统的局部稳定性。基于Lyapunov 函数的控制策略能够保证系统在大扰动下的全局稳定性。基于Lyapunov 函数的控制方法已在Buck-Boost 变换器[17]、Boost 变换器[18]、单相和三相并联交流稳压器[19-20]中成功应用。但上述应用中并未涉及DC/DC 开关变换器的指数稳定控制器，其控制的变换器非指数收敛。本文提出了一种基于Lyapunov 函数的Buck 变换器指数稳定控制器，该控制器采用不连续反馈控制方式。在该控制器控制的变换器在启动过程和受到大扰动时，有收敛速度快、过冲小等优点。

本文针对传统连续系统稳定性分析方法不能反映Buck 变换器切换时实际情况的问题，利用不连续控制理论的方法，提出一种新的Buck 变换器指数稳定性分析方法，并在分析过程中加入电路寄生参数，使得该分析方法更加接近于电路运行的实际情况。该方法不需将系统进行线性化，同时也不需要构造Lyapunov 函数对系统进行稳定性分析，可判定变换器系统在一定的切换律下达到指数稳定。本文同时提出一种用于含寄生参数连续导通模式CCM（continuous conduction mode）Buck 变换器的不连续控制器，该控制器具有全局指数稳定的特性，其瞬态响应得到显著改善。最后通过仿真和电路实验验证所提指数稳定性分析法与不连续控制器的正确性。

1 含寄生参数的Buck 变换器建模

由于建模和控制器设计过程的特殊性和复杂性，通常忽略了寄生元件。由此产生了简化的理想模型，该模型有助于理解开关变换器的主要特征。然而，寄生分量的研究对于提高模型精度和动态性能具有重要意义。使用包含寄生分量的模型可以提高稳态性能以及瞬态性能。因此，本文将电路元件寄生参数引入Buck 变换器模型中，建立Buck 变换器的含寄生参数模型。Buck 变换器工作过程如图1 所示。

图1 Buck 变换器的模态Fig.1 Modes of Buck converter

通过基尔霍夫电压和电流定律，分别对应于开关导通或关断情况的微分方程可以表示如下。

开关导通时，有

开关关断时，有

式中：iL为流过电感L 的电流；vC为输出电压；E 为输入电压；Ron、RL、RC、Vd分别对应开关管S、电感L、电容C、功率二极管D 的寄生参数。

由式（1）—式（4）可得，含寄生参数CCM Buck变换器的状态空间方程为

根据文献[21]中所提出的DC/DC 增广模型推导方法，由系统式（5）得到含寄生参数CCM Buck变换器增广周期切换系统模型为

2 基于不连续控制的Buck 变换器周期切换系统稳定性定理

由上文可知，CCM Buck 变换器是典型的切换不连续系统，文献[22]提出了一种基于不连续系统的指数稳定性分析方法，从定义上得知，该指数稳定性分析方法可应用于CCM Buck 变换器中。本文以文献[22]提出的理论为基础，分析了含寄生参数CCM Buck 变换器的指数稳定性。

2.1 周期切换不连续系统稳定性判据

考虑的切换系统为

式中：x∈Rn为状态向量；Ai=∈Rn×n和Bi=∈Rn×n（i=1，2）是常矩阵；T 为切换周期，T>0；Δτi为第i 个子系统的驻留时间，Δτi=τi-τi-1，0=τ0<τ1<…<τm-1<τm=T。显然，这是一个有m 个非线性子系统的特殊切换系统，其特点是切换时刻是周期变换的，所以称为周期切换系统。

引理1假设存在对称正定矩阵P、正常数q1、q2和α（0<α<1），使得

2.2 周期切换不连续系统稳定性判据在含寄生参数CCM Buck 变换器中的应用

对于工作在CCM 模式的Buck 变换器而言，CCM 模式的Buck 变换器是具有2 个子系统的切换系统，如系统式（11），且其2 个子系统均为线性子系统，其特点是切换时刻是周期变换的。

令i=1，2，由系统式（15）得

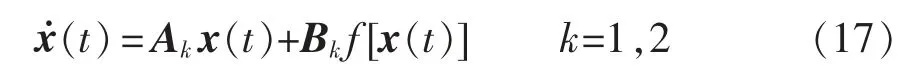
对于含寄生参数Buck 变换器系统式（6）而言，其子系统中不存在非线性项，即式（15）中，B1=B2=[0 0 0]T，在引理1 与系统式（15）中，矩阵Ei、Fi是由非线性项fi[x（t）]求得，所以，E1=E2=F1=F2=[0 0 0]T，得到简化后且适用于CCM 模式的含寄生参数Buck 变换器系统的稳定性判据。

推论1存在对称正定矩阵P 以及正常数α（0<α<1），使得

则存在小的切换周期T，使得时间切换系统式（17）的原点是全局鲁棒指数稳定的。

3 CCM 模式的含寄生参数Buck变换器指数稳定性分析

在系统式（11）中，假设该系统的工作平衡点为xd=[xd1xd21]T，则在系统式（11）工作至稳态时，其关于工作平衡点的变换后，得到关于原点工作的系统状态空间方程为

本文所用含寄生参数Buck 变换器的各参数如表1 所示。

表1 Buck 变换器的参数Tab.1 Parameters of Buck converter

将表1 中的参数代入系统式（19）后，令α 为式（19）工作至平衡点时的占空比（α=xd2/E），将式（19）代入推论1 的判据式（18）中，求解式（18）的线性矩阵不等式，可以得到对称正定矩阵P 为

所以，通过推论1 得到了该含寄生参数Buck变换器的状态空间方程系统式（19）在小切换周期T 下，是关于原点全局鲁棒指数稳定的。

4 控制器的设计、仿真与电路实验

Buck 变换器的控制目标是使输出电压尽可能接近参考信号（工作平衡点）。传统的比例积分控制方案通常采用变换器的线性化模型来设计，并被广泛用于稳定变换器。但是，由于小信号模型在每个工作点处的精度不高，在大信号扰动下表现出很差的瞬态响应。为了在大信号扰动下实现快速动态响应并获得全局指数稳定性，本文提出了基于Lyapunov 函数的控制器。该控制器使用单片机对Buck变换器进行控制。

结合式（1）～式（4），使用平均方法得到了平均模型。该模型可以表示为

式中：α 为控制系统输出的占空比（0<α<1）；分别为iL、vC在切换期间的平均值。

4.1 含寄生参数的Buck 变换器开环占空比

为了后续的推导，本文将参考电感电流设为IL，参考输出电压设为VC，并假设CCM Buck 变换器工作在稳态。将用IL与VC代替，并且在平均模型中令=0 与=0，可以得到

结合式（25）、式（26），可以得到

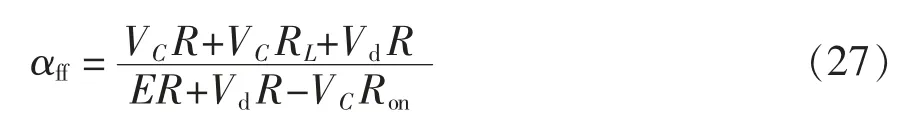
式中，αff为占空比前馈信号，αff使得变换器的输出电压紧密地跟踪参考输出电压。

4.2 基于Lyapunov 函数的控制器

为了构造基于Lyapunov 函数的控制器，首先将占空比前馈信号αff应用于变换器，并推导出运行时电感电流与输出电压的动态误差。首先推导出电感电流误差为ei=-IL，输出电压动态误差为ev=-VC，反馈控制可表示为αfb=α-αff。将ei、ev和αfb代入式（23）、式（24），可以得到

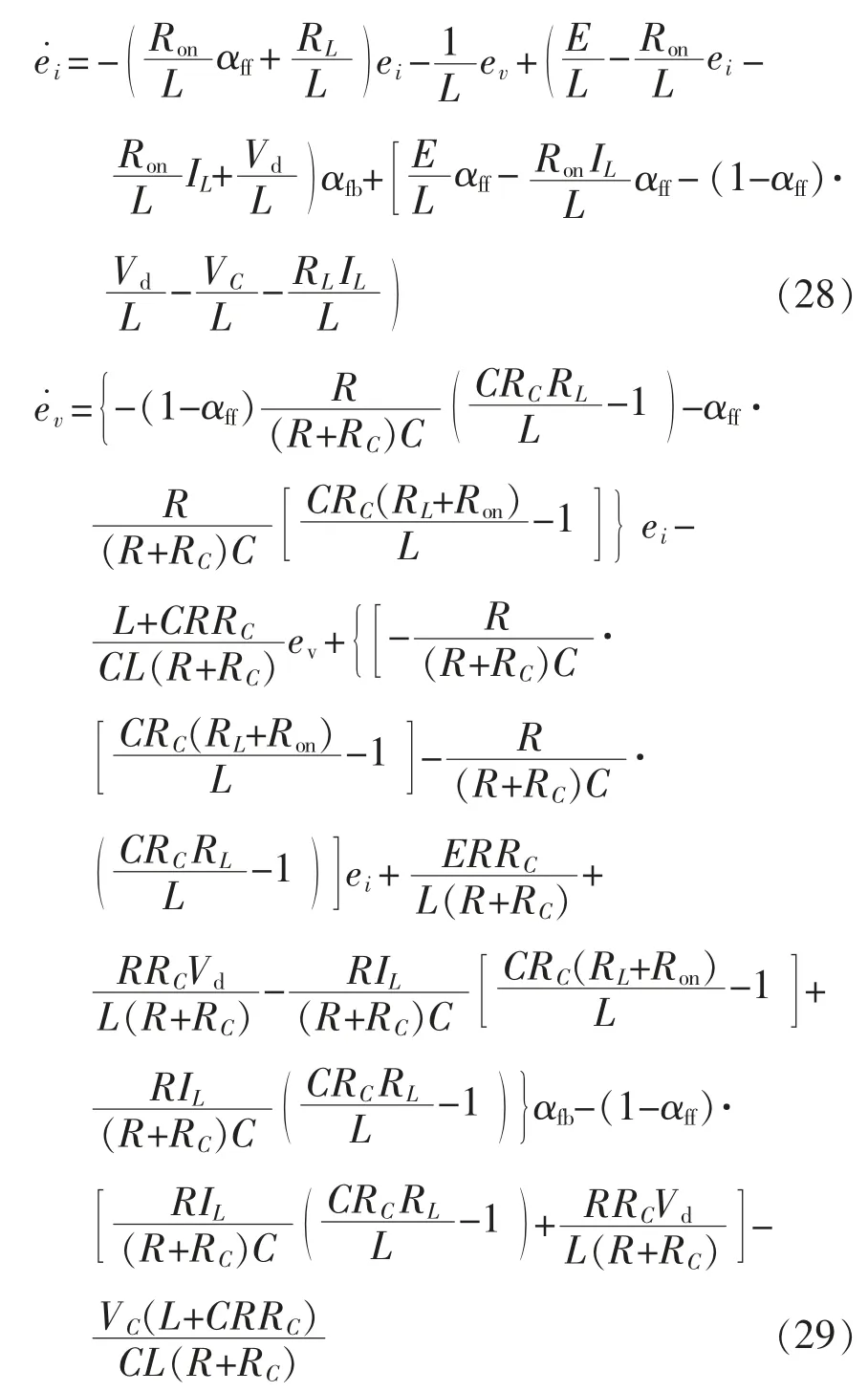
所以，系统的动态误差可以被描述为

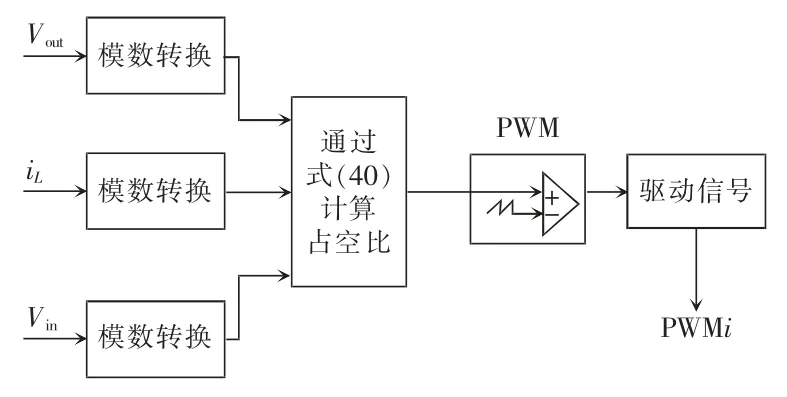
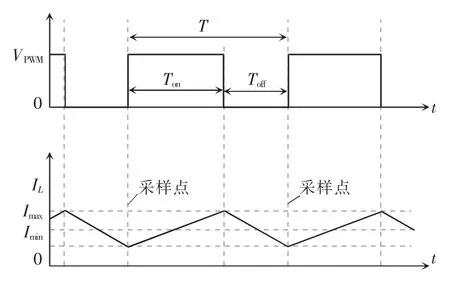
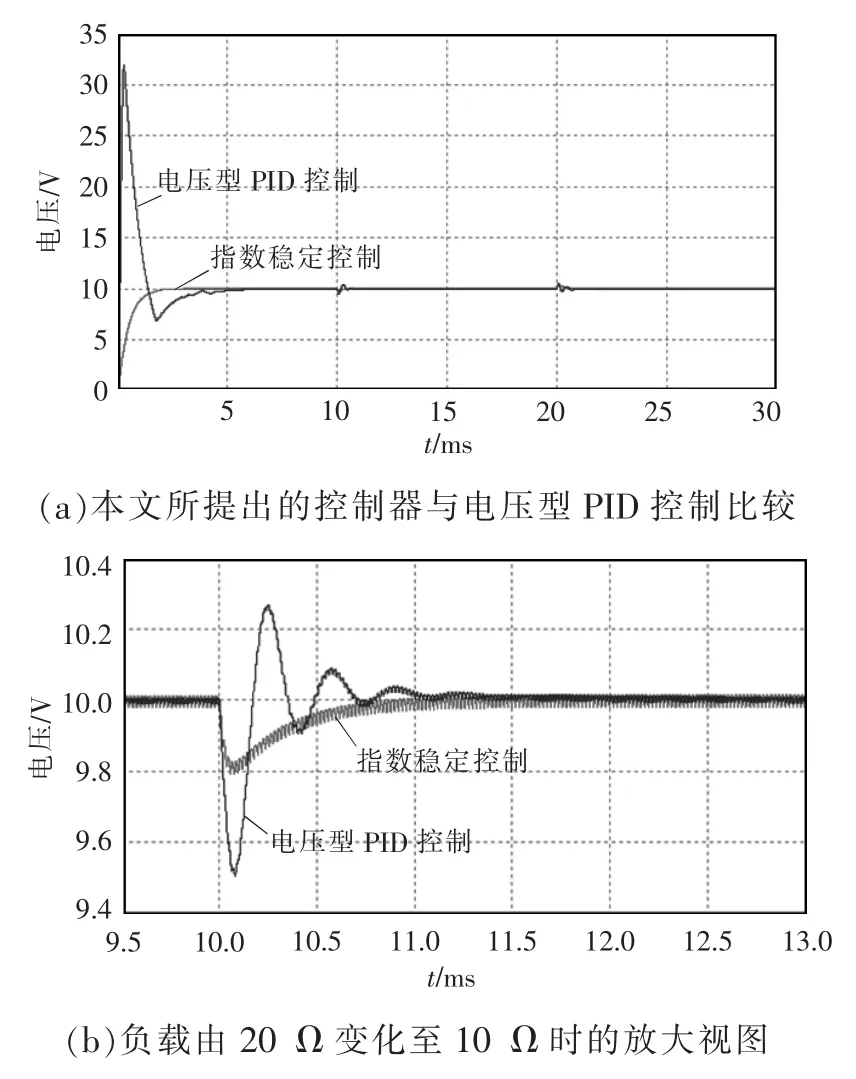
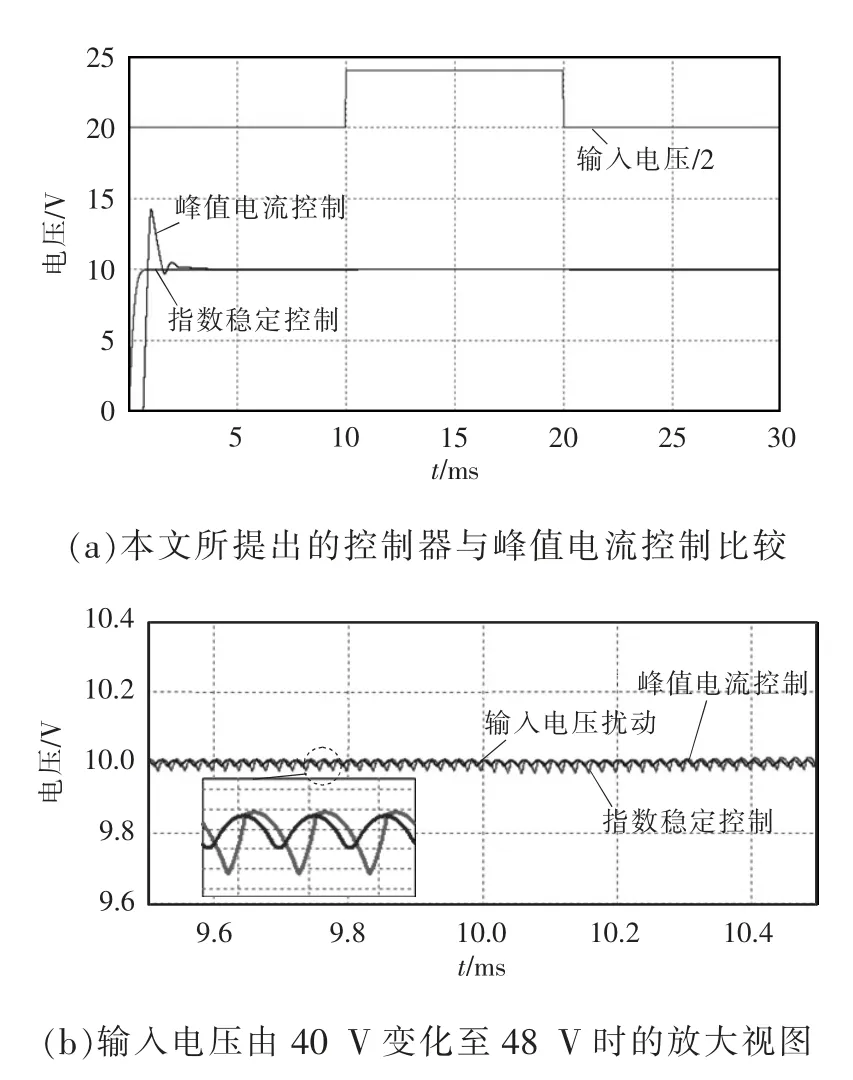
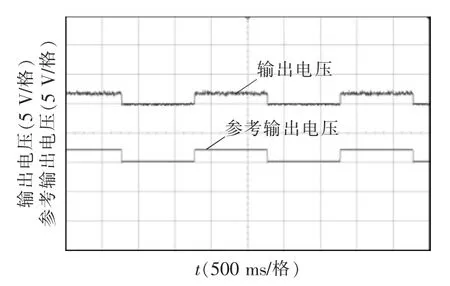
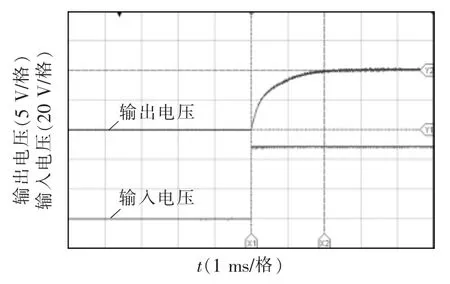
根据李雅普诺夫稳定性定理，当Lyapunov 函数V（X）满足c1||X||a≤V（X）≤c2||X||a和≤-c3||X||a，其中0

如果本文选择储存在电感和输出电容中的能量作为Lyapunov 函数

式中，P=diag[L C]。可以得到

计算其相对于时间的导数，可以得到

式中：Q=-1/2（ATP+PA）；K=1/2（BTP+PB）；F=1/2（CTPe+eTPC）。本文选择的基于Lyapunov 函数的反馈控制器为

由式（27）和式（39）确定完整的控制输入为

式中，αfb为基于Lyapunov 函数的反馈控制，在系统输出与期望值无误差的情况下，αfb=0，由αff控制变换器输出。在系统输出与期望值有误差的情况下，αfb≠0，由αff、αfb共同控制变换器输出。

上述含寄生参数Buck 变换器系统如图2 所示，其中控制系统流程如图3 所示。

图2 含寄生参数Buck 变换器系统Fig.2 Buck converter system with parasitic parameters

图3 含寄生参数Buck 变换器控制实现框图Fig.3 Block diagram of control implementation of Buck converter with parasitic parameters

4.3 仿真实验结果

基于系统式（11）的控制率式（40）在仿真软件中编写式（40）所示控制率程序。控制器采样点如图4所示，在采样点采样相关参数进行模数转换后计算该周期的占空比。选取β=0.008，分别模拟以下情况：

图4 控制器采样点Fig.4 Sampling points of controller

（1）输入电压扰动。在参考输出电压VC=10 V 和输出负载电阻R=20 Ω 的情况下，输入电压从40 V变为48 V。输入电压E 在0～0.1 s 期间设置为40 V，在0.1～0.2 s 期间设置为48 V，在0.2～0.3 s 期间设置为40 V。

（2）输出负载电阻扰动。在参考输出电压VC=10 V 和输入电压为48 V 下，输出负载R 从20 Ω 变为10 Ω。在0～0.1 s 时，输出负载电阻设置为20 Ω，在0.1～0.2 s 时，输出负载电阻R 设置为10 Ω，0.2～0.3 s期间，输出负载电阻R 设置为20 Ω。

使用表1 中电路参数在指数稳定含寄生参数的Buck 变换器中进行上述仿真实验，得到在参考输出电压、输入电压和输出负载变化时的瞬态响应。分别将本文设计的控制器与电压型PID 控制、峰值电流控制相比较。其中电压型PID 控制的参数通过文献[23]求得，其电路与波特图如图5 所示，符合文献[23]的设计要求。峰值电流控制的Buck 变换器电路及波特图如图6 所示。

图5 电压型PID 控制的CCM-Buck 变换器电路及波特图Fig.5 Circuit diagram and Bode diagram of CCMBuck converter controlled by voltage-type PID

图6 峰值电流控制的CCM-Buck 变换器电路图及波特图Fig.6 Circuit diagram and Bode diagram of CCMBuck converter under peak current control

由图5（b）中电压型PID 控制的Buck 变换器波特图可以得出，该系统的穿越频率为5.02 kHz，相位裕度为52°，满足文献[23]中关于PID 参数设计的稳定性条件。

由图6（b）中峰值电流控制的Buck 变换器的波特图可以得出，该系统的穿越频率为1.31 kHz，相位裕度为45.9°，满足文献[23]中关于PI 参数设计的稳定性条件。

CCM-Buck 变换器在输入电压变化及输出负载变化下的仿真波形如图7～图10 所示。由图7～图10 测量得出表2、表3 的结果。

表2 每个控制器在输入电压变化下的过冲百分比和稳定时间Tab.2 Percentage of overshoot and settling time under input voltage variations for each controller

表3 每个控制器在输出负载变化下的过冲百分比和稳定时间Tab.3 Percentage of overshoot and settling time under output load variations for each controller

图7 CCM-Buck 变换器在输入电压变化下的仿真波形（与电压型PID 控制的比较）Fig.7 Simulation waveforms of CCM-Buck converter under input voltage variations（compared with voltage source PID control）

图8 CCM-Buck 变换器在输出负载变化下的仿真波形（与电压型PID 控制的比较）Fig.8 Simulation waveforms of CCM-Buck converter under output load variations（compared with voltage source PID control）

图9 CCM-Buck 变换器在输入电压变化下的仿真波形（与峰值电流控制的比较）Fig.9 Simulation waveforms of CCM-Buck converter under input voltage variations（compared with peak current control）

图10 CCM-Buck 变换器在输出负载变化下的仿真波形（与峰值电流控制的比较）Fig.10 Simulation waveforms of CCM-Buck converter under output load variations（compared with peak current control）

为了对比本文所设计的指数稳定控制器的优越性能，同时与采用峰值电流控制的Buck 变换器对比进行了对比，分别仿真了变换器的启动过程与测量受到扰动时的输出电压过冲量，其对比结果如图11 所示。

图11 CCM-Buck 变换器在使用指数稳定控制器与不同控制器的启动过程比较Fig.11 Comparison of start-up process of CCM-Buck converter using exponential stability controller and other controllers

显然，由图11 可以得到指数稳定控制器与电压型PID 控制器、峰值电流控制器相比，指数稳定控制器在变换器启动时，其暂态过程的时间较另外2 种控制器更短，且过冲量为0。

4.4 电路实验

在电路实验中，测试了闭环的Buck 变换器系统在参考输出电压、输入电压和输出负载变化时的瞬态响应，参考输出电压为1 Hz 的方波电压，变化值在10～12 V 之间；输入电压为1 Hz 的方波电压，变化值在40～48 V 之间；输出负载变化值在10～20 Ω之间。实验装置如图12 所示。

图12 实验装置Fig.12 Experimental setup

Buck 变换器的电路实验控制模块由STC15 系列单片机构成，通过图2 及图3 所示编写程序实现系统的控制。图13 展示了应用本文所设计控制器时的参考输出电压变化时实际输出电压的波形。由于控制器的全局指数稳定性，即使在瞬态过程中，输出电压也能很好地跟踪参考输出电压。图14 展示了输入电压变化时实际输出电压的波形。图15展示了负载电阻变化时的实际输出电压波形。图16 展示了变换器启动期间实际输出电压和输入电压的波形。在启动瞬态过程中，控制器可以快速跟踪低过冲的参考输出电压。由以上结果可知，本文所设计的Buck 变换器的指数稳定控制器电路实验与计算结果、仿真结果相符。

图13 采用本文设计的控制器时，CCM-Buck 变换器在参考输出电压变化下的实验波形Fig.13 Experimental waveforms of CCM-Buck converter under reference output voltage variations when the proposed controller is used

图14 采用本文设计的控制器时，CCM-Buck 变换器在输入电压变化下的实验波形Fig.14 Experimental waveforms of CCM-Buck converter under input voltage variations when the proposed controller is used

图15 采用本文设计的控制器时，CCM-Buck 变换器输出负载变化时的实验波形Fig.15 Experimental waveforms of CCM-Buck converter under output load variations when the proposed controller is used

图16 采用本文设计的控制器时，CCM-Buck 变换器在系统启动过程中的实验波形Fig.16 Experimental waveforms of CCM-Buck converter during system startup when the proposed controller is used

5 结语

本文提出了一种新的含寄生参数Buck 变换器的指数稳定性分析方法，该方法以非线性系统不连续控制的指数稳定性判据为基础，推导得到了含寄生参数Buck 变换器的指数稳定性判据。此方法可通过简单的线性矩阵不等式计算得到含寄生参数Buck 变换器的指数稳定性，没有近似处理，分析控制更接近实际情况。从仿真实验与电路实验中可以看出，指数稳定性较一般的稳定性相比具有动态响应快的特点，该方法可推广至一系列开关变换器中。本文也设计了一种指数稳定的含寄生参数Buck 变换器的不连续控制器，该控制器采用不连续控制方式控制Buck 变换器。不连续控制器较一般的线性控制器而言，由于没有近似处理不连续控制器，具有设计过程简单、动态响应性能好、过冲现象小等特点。不连续控制器应用于含寄生参数Buck变换器中，其特性更符合含寄生参数Buck 变换器的非线性特性。最后通过仿真实验与电路实验验证了本文所提指数稳定性分析方法及该不连续控制器的正确性与优越性。