基于特征标记的多尺度建筑空间图像分解仿真

李 莹，李险峰

(吉林建筑大学，吉林 长春 130118)

1 引言

多尺度多分辨率是人类高效工作与视觉精准的重要特征之一。自然产生的图像里很大一部分都具有不同尺度的信息，这些信息会同一时间出现在图像里。而对图像的使用研究，一般都会局限在某些尺度或只需要某个尺度的信息，而其他尺度信息通常会对图像的结构造成不好的影响，因此将图像信息按照尺度进行分解是较为关键的。多尺度图像分解能够删除一些无用的图像信息，使其不能对图像处理结果产生不良影响，也能够减少图像处理的复杂程度与难度，其也是图像边缘识别与图像检测等处理过程的预处理算法之一。

目前较为经典的图像分解方法能够大致分为两种即：最小二乘分解法与经验模式分解法，这两种方法在图像分解时能够保留边界图像的平滑，但其较为偏向于图像分解的单一像素分解。这就导致分解图像后，只能分解出部分需要的信息，并不能将整体图像进行分解。

针对上述问题，本文提出一种基于特征标记的多尺度建筑空间图像分解方法，凭借对偶范数构建分解模型，获取图像的极值点把图像的坐标垂直投射至坐标平面内，组建包络的上界，并迭代该流程直至产生包络下界，实现对多尺度建筑空间图像的分解。

2 特征标记下多尺度建筑空间图像分解

2.1 基于特征标记的图像视觉描述

特征标记定义的视觉描述有：形状、颜色、位置、纹理、运动与其他特征标记符。

颜色即视觉表现力[1]最大的特征，在过去十几年的图像研究中被广泛使用。特征标记支持的颜色空间有：HSV、RGB与单色空间。拟定标记符存在可伸缩颜色、主流色、颜色布局与颜色结构。本文使用的颜色特征标记符即主流色标记符与颜色空间标记符，依靠两种标记符显示边界，如果将两种标记符融合起来使用能够更好的标记图像的全局颜色与局部颜色。

1)主流的标记符

该标记符用作标记一幅图像或一种随机形状包含的几种主导颜色[2]，指出了代表颜色、拟定区域内占据的百分比、主色的空间关联性与主色的颜色方差。

标记符能够被定义成

F={{ci，pi，vi}，s}(i=1，2，…，N)

(1)

式中，ci代表主颜色，pi代表颜色表粉笔，vi代表一种可选量，i代表颜色方差，s代表主色在拟定区域内的整体空间关联性与凝聚性。

2)颜色空间标记符

该标记符用作标记整幅图像或随机图像区域的颜色空间分布[3]特征情况，使用的是量化至8bits的YCbCr颜色空间，其量化方程如下所示

(2)

颜色空间标记符的标记流程能够分为两个部分：基于网格的标记颜色选取与DCT(Discrete Cosine Transform，离散余弦变换)的变换与量化。

具体流程如下所示：拟定一幅多尺度建筑空间图像，首先将图像通过颜色空间映射[4]至YCbCr空间内，随后将图像划分成8×8的图像块，对小图像块的每个颜色进行分量，并计算其颜色平均值当做标记颜色，最后对所有主色快的颜色分量进行DCT转换，获得系数矩阵，对系数进行量化，同时进行扫描，获取颜色空间标记符的值。对主色的颜色分量进行DCT转换，同时把图像标记的特征细节部分数据集中在左上角，越靠近反方向的数据即不明显的高频数据[5]，便于挑选不同的精度来进行特征标记符的提取。

纹理与颜色相同，也是图像内非常关键的一种底层视觉特征，在图像检索与浏览应用中起到了至关重要的作用。特征标记拟定了三种纹理标记符：

第一种即纹理浏览标记符，其作用即标记纹理的感知属性，例如规则性、方向性与粗糙度等，在图像检索领域内有着广泛的使用，能够进行纹理图像的快速检索。

第二种即同质纹理标记符，其是基于纹理的局部空间频率标记，为相似性检索供给了一种同质纹理的定量标记。最后一种即局部轮廓直方图标记符，在标记纹理分布[6]不均匀的图像时作用非常大。本文内，使用了纹理浏览标记符与轮廓直方图标记符对多尺度建筑空间图像的纹理特征进行标记。

3)纹理浏览标记符

该标记符即一种极为紧凑的标记符，最大需要12bit来标记纹理的方向性、粗糙度与规则性。由于多尺度建筑空间图像的纹理可能存在多于一个的方向与粗糙程度，因此特征标记定义内，允许存在两种不同的粗糙度与方向。纹理的规则性在0～3之间，0即随机或不规则的纹理，3就是具有一致性的方向性与粗糙度的周期纹理，其处于两个值之间且具有较好的灵活性。

4)轮廓直方图标记符

轮廓直方图标记符即轮廓的空间分布，在浏览与检索轮廓分布不均匀的图像时非常有用。特征标记定义的轮廓直方图标记符描述了不同种类的边缘空间分布，包括四种方向轮廓与一种无方向轮廓。

①把图像平均分为4×4共16种子图，运算所有子图的局部轮廓直方图。所有局部轮廓直方图存在5种bins，这5种bins分别表示为水平、垂直、135度、45度与无特定方向的轮廓分布，因此直方图共存在80种bins。

②进一步将16种子图像划分成更小的图像块。图像块的总量是固定的，一般是2的幂，其尺寸和图像的尺寸存在关联。

③将所有图像块划分为2×2个图像区域，所有区域的颜色值通过区域里所有像素的颜色均值进行运算，随后通过特征标记推荐的5个轮廓检测算法对所有图像块[7]进行运算，如果运算出的最大轮廓强度超出某个阈值，那么该轮廓种类就作为图像块的边缘，并应用在直方图的计算内，统计所有图像块的轮廓种类就能够获得所有子图的局部轮廓直方图。

④对获得的值进行量化与归一化处理。对归一化之后的80种bins的值进行非线性量化之后，所有bin通过3bits进行编码，这样就需要240bits来描述一个轮廓直方图标记符。

2.2 基于特征标记的分解模型建立

2.2.1 模型提出

为了克服全变差重组图像时引起的阶梯现象[8]，本文提出一种新模型，基于对偶范数的多尺寸建筑空间图像分解模型，构建分解模型。其定义为

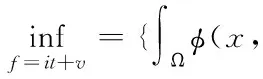
(3)

实际中，由于*范数求解较为困难，因此最小化式(3)是较为困难的，本文通过Meyer模型逼近式(3)能够获得

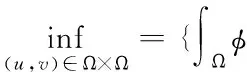
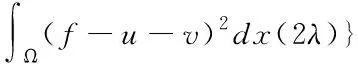
(4)

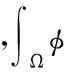
式(4)依赖于图像的梯度大小，架构成分的最小化能量介于全变差半范数与W1，2=H1范数之间，纹理成分的最小化能够介于他们的对偶范数，G范数与W-1，2=H-1范数之间。u与v之间的对偶性使得分解模型在处理图像的轮廓与纹理时可以自适应调节，缩减了图像内产生的阶梯现象。

2.2.2 投影算法下全变差最小化

本文通过非线性投影[10]算法最小化全变差，其需要解决的问题如下所示

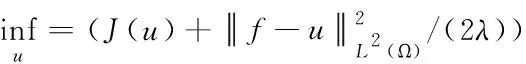
(5)

针对式(5)的求解给出以下命题：

式(5)的解如下所示

u=f-PμBG(f)

(6)

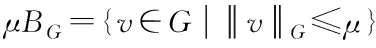
拟定一种计算投影PμBG(f)的算法，该算法可用于求解以下最小化问题

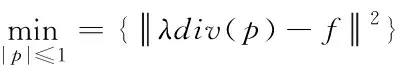
(7)

拟定输入图像的尺寸是N×N，那么这个问题能够通过以下固定点算法获得

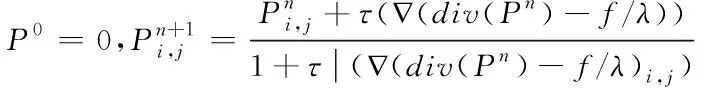
(8)

确保概算法Soulian的一种充分条件如下：

拟定式(8)内的参数τ满足τ≤1/8，那么在n→+∞时，λdiv(Pn)会收敛到PμBG(f)。

2.3 多尺度建筑空间图像极值点求解

多尺度建筑空间图像数据拟定为f(i，j)，极值点[11]的计算规则即，当前像素点灰度值f(i，j)和其邻域灰度值进行对比，如果f(i，j)超过其邻域灰度值该点就是极大值，反之即极小值。针对图像边界点只需要和其邻域点对比即可。

2.4 曲面差值求取

曲面差值方法，和以往对插值漏点处理的算法不同。由于进行极值点三角剖分差值之后，图像信息会构成一种凸曲面，该曲面不会覆盖图像的信息空间[12]这就导至图像产生了漏点的情况发生，针对漏点的处理，会直接干扰图像分解的准确程度。本文凭借对称处理方法，评测漏点灰度值。其流程如下：

1)搜索三角剖分与样条差值曲面的边界点；

2)搜索距离漏点f(i1，j1)最近的边界点u(i2，j2)；

3)在差值凸曲面里搜索以边界点u(i2，j2)为中心和漏点f(i1，j1)对称的点f′(2i2-i1，2j2-j1)，依靠该点f′(2i2-i1，2j2-j1)的灰度值当作漏点f(i1，j1)灰度值的估测结果。

2.5 多尺度建筑空间图像分解

拟定图像表面比作朗伯面，那么图像能够被认为是一种实际物理目标结构模式，通过入射光调制所组成的图像。这样就能够凭借经验模式分解算法对多尺度建筑空间图像进行分解。

首先，凭借二维图像的实际大小标定图像所处平面Oxy的位置，图像相应像素的灰度值拟定成Z坐标，把图像的Z坐标垂直投射至Oxy坐标平面内，最后在投影面内进行局部极值点的挑选、三角剖分与三角差值曲面处理。按照特征标记定义，通过所有的局部极大值对图像进行平面三角剖分，组建差值曲面当做包络的上界，同时局部极小值迭代该流程，直至出现包络的下界停止，然后采集极大值与极大值包络曲面的代数均值，用在图像的分解处理内。

设定∀F(x，y)代表预处理的多尺度建筑空间图像，将极小值与极大值包络曲面的代数均值描述成m1(x，y)，标记图像F(x，y)和m1(x，y)的差值为h1(x，y)。

h1(x，y)=F(x，y)-m1(x，y)

(9)

其中，h1(x，y)代表F(x，y)的一种中间流程值，迭代上述流程k次，直至h1k成为一种内禀性模式函数

h1(k-1)(x，y)-m1k(x，y)=h1k(x，y)

(10)

定义

D1(x，y)=h1k(x，y)

(11)

式中，D1(x，y)代表分离出的第一种内禀性模式函数，随后将D1(x，y)从初始数据内剥离，能够得到

F(x，y)-D1(x，y)=R1(x，y)

(12)

把R1(x，y)当做新的数据，迭代上述流程n次，其迭代关联为

R1(x，y)-D2(x，y)=R2(x，y)，…，

Rn-1(x，y)-Dn(x，y)=Rn(x，y)

(13)

最后获得的描述式即

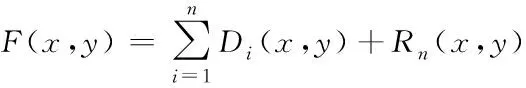
(14)

式中，F(x，y)即原图像信息，Di(x，y)表示尺度分离后获取的尺度细节信息，Rn(x，y)表示获取的最终大尺度趋势项。

上述运算能够对不规则的图像振幅进行平滑，减少数据奇异性，将图像依靠尺寸分解为一些大尺度趋势信息。细节信息表示了骑行波与图像纹理这类小尺度信息，基础变化趋势信息与图像基础结构则表示了大尺度信息。分别对不同尺度信息进行目标识别等深入处理，就能够获得基于不同尺度的分解结果。

3 仿真实验证明

为了证明所提方法的有效性，进行实验，实验环境为：混凝土材料参考高等级公路路肩，对混凝土材料的比例与条件进行挑选，指定成标准实验块以供实验。数字储存示波器，型号为HP5-6401A型，该仪器主要负责数据波形的采集，数字频率计数器使用E323。

实验1：多尺度建筑空间图像的特征标记

首先需要从资源库内随机提取一幅建筑图像，作为实验原图像，对其进行特征标记。

图2 多尺度建筑空间特征标记

通过图1能够看出，图像的所有存在特征的点已经通过白色的圆标记出来，这些圆清晰地组成了建筑空间内物体的大致架构，同时标记清晰，并且这些标记能够被移动，因此不会对图像造成较大的缺损，通过图1能够证明所提方法在多尺度建筑空间图像分解中，的表现较为优异。

实验2：多尺度建筑空间图像的纹理分解

使用图2作为图像纹理分解的源图像，利用所提方法对该图像的纹理进行分解，分解的结果如图3所示。

图3 所提方法分解建筑空间图像纹理结果

通过图3能够看出，所提方法所标记出的特征非常清晰，且标记的轮廓较为完整，并不存在较大缺陷。这是因为所提方法，能够通过特征标记定义，缩减图像内产生的阶梯现象，使后期分解图像时的图像特征更为完整、明显。

实验3：建筑空间图像像素分解

通过图4能够看出，所提方法分解出的像素，存在较为显著的区别性，同时像素图内，噪声存在量较少，不会对分解结果产生影响。

4 结束语

为了获取建筑空间图像内的关键信息、提出冗余信息，提出一种基于特征标记的多尺度建筑空间图像分解方法，该方法依靠特征标记与曲面差值，实现对多尺度图像的分解。但由于所提方法只偏向于对图像的分解，因此并没有设计针对图像储存的数据库，而分解出的无用图像与分解结果，都需要直接剔除或使用，这就导致算法的运行过程中，需要依靠工作人员实时协助，会消耗大量的人力资源。因此，下一步所需要研究的课题即：在所提方法的基础上，增添不同种类的资源储存库，以存放分解结果与无用图像，真正实现算法的自动化运行。