T型微通道内液滴在幂律流体中运动机理的格子Boltzmann方法研究*

刘 浩，娄 钦，黄一帆

（1.上海理工大学 能源与动力工程学院，上海 200093；2.上海市动力工程多相流动与传热重点实验室，上海 200093）

引 言

近几十年来，微流控技术制备液滴由于具有安全性高、易于控制、大小均一，以及单分散性好等众多优点而迅速发展，并得到了工业界与学术界的广泛关注.工业上，制备液滴微流控的常见通道有T 型通道、双T 型通道、十字型通道和Y 型通道等.其中T 型微通道装置因结构简单、加工容易等性能已在药物输运[1]、单细胞分析[2]、液滴微反应器[3]等领域取得了广泛的应用.

近年来众多学者研究了T 型微通道内液滴产生的机理.Zhao 等[4]用实验方法研究了毛细数、黏度比、流量比以及通道管径对液滴尺寸的影响，发现了与所研究的其他因素相比，流量比对液滴形成尺寸的影响更大.Han 等[5]用数值方法研究了流量比、连续相黏度、界面张力以及接触角对三维T 型微通道内液滴形成尺寸的影响，发现形成液滴的尺寸随流量比和界面张力的增大而增大，随连续相黏度和接触角的增大而减小.另一方面，一些学者研究了壁面润湿性对液滴形成的影响.Li 等[6]用VOF(volume of fluid)研究了疏水表面上液滴的形成过程.发现截面的速度分布随着滑移长度的增加越来越平坦，同时垂直于T 型微通道壁面的速度梯度越来越小，液滴直径越来越大.Shi 等[7]用格子Boltzmann 方法(lattice Boltzmann method，LBM)研究了流量比、毛细数Ca、几何形状以及润湿性对T 型微通道内液滴形成尺寸和形状的影响.研究发现，液滴尺寸和形状不仅取决于流量比、Ca等流体性质，还取决于T 型通道的几何形状和壁面润湿性.除了液滴形成尺寸外，还有一部分学者研究了液滴的流型分布.Liu 等[8]研究了不同润湿性时，Ca、流量比、黏度比对T 型微通道内流型的影响，得到了液滴流型从挤压（squeezing regime）转变到液滴（dripping regime）的临界Ca，并发现该临界Ca与流量比、黏度比和接触角无关.Fallah 等[9]在研究T 型微通道内Newton 液滴在Newton 流体中形成机理时，观察到了三种流型(平行(parallel regime)、挤压和液滴)，并发现了微通道几何形状对液滴大小和液滴之间的距离有很大影响.

以上工作都是基于Newton 液滴在Newton 流体中形成机理而开展的，现实生活与工业应用中广泛存在着T 型微通道中Newton 液滴在非Newton 流体中运动的现象.近年来，已有大量学者研究了Newton 液滴在非Newton 流体中运动过程.Glawdel 等[10]采用实验方法观察到了T 型微通道内Newton 液滴在非Newton 流体中形成的三个阶段：填充阶段、颈缩阶段以及滞后阶段.他们认为滞后阶段是液滴形成后界面回缩的主要原因.Fu 等[11]观察到了T 型微通道内非Newton 流体的四种典型的流型：段塞流、液滴流、射流以及平行流，并指出非Newton 流体的浓度越大液滴流和平行流的区域越大.黄一帆等[12]采用LBM 研究了幂律流体液滴在T 型微通道内运动及流型变化，结果表明，非Newton 流体液滴在T 型通道内存在阻塞破裂、隧道破裂和不破裂三种流型.以上的学者主要研究了液滴在非Newton 流体的流型，对于液滴的形成机理并未系统研究.Sang 等[13]研究了黏度比对非Newton 液滴在Newton 流体中形成尺寸的影响，发现了在幂律流体中，液滴直径随黏度比和幂律指数的增大而减小；在Bingham 流体中，液滴体积随黏度变化不大，但随着屈服应力的增大，液滴延伸明显增大.Sontti 等[14]用CFD(computational fluid dynamics)分析了幂律流体的幂律指数、Newton 流体和幂律流体流量变化以及两相表面张力对液滴形成尺寸的影响，发现了幂律流体的幂律指数越大，产生的液滴尺寸越小；表面张力越大，产生的液滴尺寸越小；并且Newton 相和非Newton 幂律流体相的流量比对产生的液滴尺寸有显著影响.目前已有相关文献用LBM 研究液滴在幂律流体中的运动规律.Chiarello等[15]通过LBM 研究了T 型微通道内液滴在剪切变稀流体内的运动过程，主要分析了Ca和流量比对液滴尺寸的影响，得到的结果和实验结果一致.Gupta 等[16]用LBM 研究了Ca较小时液滴在黏弹性流体和Newton 流体中运动时尺寸的变化.Shi 等[17]用LBM 研究了幂律指数n、表面张力、两相黏度比对T 型微通道内Newton 液滴在非Newton 流体中形成的影响，结果表明液滴尺寸、液滴产生频率和液滴脱离点均随幂律指数的变化而变化.

以上研究工作说明，T 型微通道中流变参数，如Ca、黏度比和流量比对T 型微通道内液滴的形成机理有重要的影响.然而目前的研究工作中存在幂律指数范围较小，流变参数考虑不全面以及管道内润湿性问题考虑较少等不足，鉴于此，本文采用LBM 进一步研究了T 型微通道中液滴在幂律流体中的形成机理，主要研究了幂律指数n、Ca、两相流量比Q、两相黏度比M以及主管道固体壁面的润湿性（润湿性大小用接触角θ 来表征）对液滴的形成尺寸、形成时间以及变形参数的影响.

1 不可压幂律流体格子Boltzmann 模型

LBM 已被证明是一种有效的模拟复杂流动的方法[18-21]，相对于传统数值模拟方法，LBM 具有计算效率高、处理复杂结构时稳定性好等优点，被众多学者用来研究多相流动等问题.本文采用Lou 等[22]提出的非Newton 不可压两相流模型研究T 型微通道内液滴在幂律流体中的形成机理.

1.1 格子Boltzmann 模型

在Lou 等提出的非Newton 不可压两相流模型中用两个分布函数，例如指标分布函数fα和压力分布函数gα，分别描述指标参数和速度/压力的演化过程，两个分布函数可以写为以下形式：

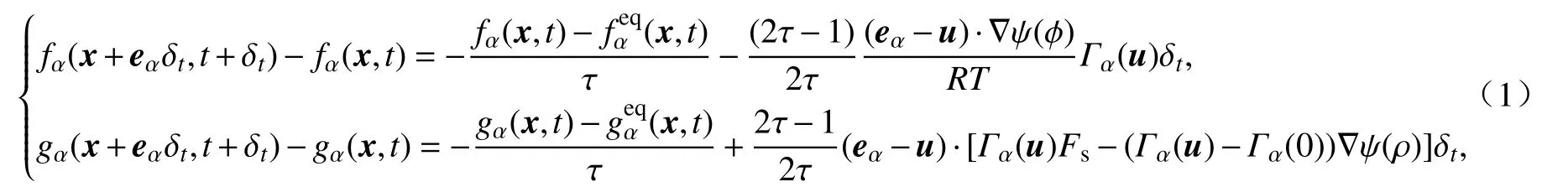
其中α=0,1,2,···,b-1,b为离散速度方向个数；x和t分别表示粒子运动的位置和时间；δt代表时间步长，τ为松弛时间，其由运动黏度ν相关决定，运动黏度系数和松弛时间τ之间关系为ν=(τ-0.5)c2sδt，这里是与格子速度c=dx/dt相关的常数；eα表示离散速度；φ, ρ,u分别代表指标函数、流体密度和流体速度；Fs表示与表面张力相关的力，Fs=κρ∇∇2ρ，κ代表表面张力强度系数；ψ(ρ) =p-ρc2s，其中p为流体压力，演化方程(1)中ψ(ϕ)和状态方程相关，本文采用Carnahan-Starling[23]状态方程，对应的ψ(ϕ)为如下形式：

其中a决定分子间相互吸引力强度，R为气体体积常数，T为流体温度.在演化方程(1)中，函数Γα(u)表达式为

其中 ωα为权重系数.演化方程(1)中fαeq(x,t)和geαq(x,t)是对应的平衡态分布函数，形式如下：

宏观量指标参数ϕ、压力p以及速度u的统计由下面方程给出

流体密度ρ(ϕ)和运动黏度ν(ϕ)可由指标参数ϕ计算得到：

其中 ρg和 ρl分别代表气相流体和液相流体密度，ϕh和 ϕl为指标参数的最大值和最小值，可由Maxwell 重构得到.通过Chapman-Enskog 分析还可以得到方程(1)对应的宏观动力学方程：

其中 Π是黏性应力张量，Π =η(∇u+u∇)，其中η为动力黏度，对于幂律流体η可以写为

其中γ为剪切速率，η0为稠度系数，

为应变率张量，n为非Newton 流体幂律指数.当n＜1 时，流体为剪切变稀流体，即其动力黏度η随着剪切速率γ的增大而减小；当n＞1 时，流体为剪切变稠流体，其动力黏度η随着剪切速率γ的增大而增大；当n= 1 时，流体就是通常的Newton 流体，其动力黏度η保持为一个定值，此时η=η0=ρv.因此，根据n的取值来区分流体是Newton 流体还是幂律流体.

本文使用D2Q9 模型来进行数值模拟研究，权重系数 ωα设置为：当α=0时，ωα=4/9；当α=1 ～4时，ωα=1/9；当α=5 ～8 时，ωα=1/36.eα为离散速度，表达式为

关于梯度和Laplace 算子的离散方法采用二阶中心各向同性方法(ICS)[24]：

1.2 润湿性边界条件

润湿现象是指流体与壁面接触时的铺展现象，其涉及流体与固体之间相互作用，该现象的强弱程度可由固体壁面接触角的大小来衡量.在LBM 中，壁面的润湿性由润湿性边界条件来描述.本文采用由Davies 等[25]提出的润湿性边界条件，与其他润湿性边界条件相比，该润湿性边界具有格式简单，非常容易扩展到其他模型并很方便应用到复杂壁面上等优点[26-27]；该边界条件采用表面亲和的概念表示润湿性的大小.表面亲和力被定义为

其中 σs1代表固-液表面张力； σs2为固-气表面张力； σ12为气-液表面张力.

2 模型验证

2.1 Laplace 定律验证

本节采用Laplace 定律验证模型的正确性.初始时在网格数为128 × 128 区域中心内放置半径r、密度为ρd=0.5的静止非Newton 流体圆形液滴，其余区域充满密度ρc=0.1的Newton 流体，计算域四周的边界条件均为周期性边界条件.

根据Laplace 定律可知，当系统达到稳定时表面张力 σ恒定，且液滴内外的压力差ΔP=Pi-Po与半径的倒数1/r呈线性关系，关系式如下：

为了验证Laplace 定律，在数值模拟中分别考虑了r= 16，20，24，28 和32 五种情况.为了保证模拟结果具有一般性，对于每种情况都研究了幂律指数分别为n= 0.8，n= 1.0 和n= 1.2 三种情况.图1 给出了在三种幂律指数下得到的液滴内外压力差ΔP与半径倒数1/r的关系，结果可知，对于所有的幂律指数n，模拟结果与Laplace 定律均一致.

图1 液滴内外压力差ΔP 和半径倒数1/r 之间的关系Fig.1 Relationships between pressure jump across the droplet interface ΔP and inverse of droplet radius 1/r

2.2 固壁面润湿性验证

本小节对幂律流体剪切变稀流体液滴的静态接触角进行验证.数值模拟的计算区域为Lx×Ly= 128 × 63，在计算区域下边界中心放置半径r= 18，密度ρc=0.5以及幂律指数n= 0.8 的非Newton 流体半圆液滴，液滴周围充满密度为ρd=0.1的Newton 流体，初始时刻，气液两相的运动黏度均为νd=νc=1/6.边界条件设置为：上下固壁面为无滑移边界条件，左右为周期边界条件.

从图2 可以看出，当数值模拟达到稳定，固壁面静态接触角 θeq分别为30°，90°和150°时，模拟得到的接触角θ 结果分别为31.3°，92.7°和148.9°.结果与润湿性边界吻合较好.

图2 不同静态接触角θeq 得到的稳态接触角Fig.2 Steady state contact angles obtained with different values of static contact angle θeq

2.3 幂律流体中液滴的变形

本小节对幂律流体中液滴的变形进行验证，如图3 所示，数值模拟的计算区域为Lx×Ly= 180 × 80，半径r= 20 的Newton 液滴置于两平板中心位置，液滴周围为幂律流体；两个平板以大小相同，方向相反的速度移动.边界条件设置为：上下固壁面为无滑移边界条件，左右为周期边界条件.对于该问题，当Re和Ca较小时，液滴最终变形为椭圆形，并且液滴可由变形参数[14]量化，液滴的变形参数定义为

图3 液滴在幂律流体中的示意图Fig.3 The illustration of a single droplet in a power-law fluid

其中Lc和H分别是当液滴的形状稳定时对应的长度和宽度，DI= 0 时，得到的液滴为球形.

在数值模拟中，研究三种幂律流体(n= 0.5，1.0，1.5)中Ca对液滴变形的影响，每种幂律流体分别计算了Ca为0.05，0.1，0.15，0.2 和0.25 的情况，其余无量纲参数为Re= 0.1，黏度比为1.图4 展示了本文中得到的不同幂律指数n下液滴变形参数与Ca的关系，并与文献[28]中得到的结果进行了对比.从图中结果可以发现，本文得到的结果与文献[28]的结果一致，说明本文所采用的模型可以很好地模拟液滴在非Newton 幂律流体中的运动行为.

图4 不同幂律指数下，液滴的变形参数DI 与Ca 的关系Fig.4 Deformation parameter DI as a function of the capillary number for different power-law fluids

3 模拟结果与分析

本文所研究的物理问题如图5 所示，T 型微通道的主管道宽度为Wc，长度为L，而T 型微管道的子管道宽度为Wd，长度为Yd，主管道进口到子管道的距离为Yc，初始时，主管道内部充满非Newton 流体，而子管道内部充满Newton 流体.边界条件设置为：主管道与子管道进口为呈抛物线分布的速度边界，其中主管道和子管道沿流动方向的最大速度分别为Uc和Ud.主管道出口为自由边界条件，其他固壁均为无滑移边界条件.在数值模拟中，主管道和子管道宽度Wc和Wd均为30，L= 820，Yc= 75，Yd= 120.主管道幂律流体密度 ρc= 0.1，子管道Newton 液体的密度ρd=0.5，运动黏度νd=0.01.速度边界条件和无滑移边界条件采用半反弹边界处理方法[29]，自由边界采用对流边界条件处理[30].

图5 T 型微通道物理模型Fig.5 The physical model for the T-junction microchannel

在本文中，决定该问题运动特性的无量纲数为毛细数Ca、主管道与子管道流量比Q和两相黏度比M，分别表示为

式中 ηd和 ηc分别代表子管道动力黏度和主管道动力黏度，ηd=ρdνd，ηc=ρcνc，σ为气液两相表面张力.此外，在下文中我们通过分析液滴尺寸、形成时间以及变形参数揭示T 型微通道中液滴在非Newton 流体中的形成机理.其中液滴的形成时间定义为液滴在T 型管道拐点处断裂的时间.如无特殊说明，本文中所用单位均为格子单位.

3.1 幂律指数n 对液滴形成的影响

本小节研究主管道内幂律流体的幂律指数n对子管道内液滴形成的影响.在数值模型中，固定Ca= 0.004 29，初始黏度比M=1.98，流量比Q=10，ηd=0.005，固体壁面为完全润湿性表面(θ =180°).

图6 给出了五种不同主管道幂律指数n（n= 0.6，0.8，1.0，1.2，1.4）得到的液滴运动过程图，其中每种情况第一幅图中的时刻为液滴刚好形成的时刻，第二幅图为流动达到稳态时的液滴形态图.从图中可以发现看出，主管道幂律指数n较小时，子管道流体进入主管道形成较大的液滴，堵塞主管道，即液滴流型呈挤压状；随着幂律指数的增加，子管道中液滴的宽度小于主管道的宽度，流型呈液滴状.

图6 T 型微通道内主管道流体不同幂律指数液滴形成过程Fig.6 The droplet formation process of the continuous phase fluid with different power-law indexes in the T-junction microchannel

从以上结果还发现随着主管道流体幂律指数n的增大，液滴形成的时间减少，这一结论和文献[17]中结论一致.这是因为随着幂律指数的增加，流场的表观黏度明显的增大，主管道非Newton 流体的高黏度增加了剪切应力，使得液滴分离时间越来越短.

为了量化幂律指数n对液滴形成机理的影响，图7 给出了不同幂律指数n时得到的液滴尺寸、形成时间以及变形参数.从图中可以看出，随着主管道幂律指数n的增大，子管道流体在主管道内形成的液滴尺寸近似呈线性减小(图7(a))，同时液滴在主管道内形成的时间越短(图7(b)).另一方面随幂律指数n的增加，液滴的变形参数越来越小(图7(c))；且随着幂律指数n的增加，液滴形成的时间和变形参数变化非常慢.这是因为幂律指数大于1 时，流体的黏度明显增大，子管道流体的惯性力大于主管道黏性力，使得液滴的分离时间提前，在主管道得到体积更小的液滴，此时液滴由于体积较小受到的剪切力也变小，对应地，液滴的形状基本为球状，并且形状大小近似不变，因此变形参数变化非常慢.

图7 主管道流体幂律指数n 对液滴的影响：(a)尺寸；(b)形成时间；(c)变形参数Fig.7 The effects of continuous phase power-law index n on the droplet: (a) the size; (b) the formation time; (c) the deformation index

3.2 毛细数Ca 对液滴形成的影响

本小节研究主管道非Newton 幂律流体的Ca对液滴形成的影响.主要研究了Ca分别为0.003 43，0.005 15和0.006 87 对液滴尺寸、形成时间以及变形参数的影响，每种情况都研究了剪切变稀、Newton 和剪切变稠三种情况，初始黏度比M= 1.98，流量比Q= 10，固壁面为完全润湿性表面.

图8～10 给出了不同Ca下，主管道流体为剪切变稀、Newton 以及剪切变稠时液滴形成的过程图.从图中可以看出，无论主管道为剪切变稀、Newton 以及剪切变稠时，都有主管道幂律流体的Ca越大，形成的液滴尺寸越小，且与前人研究的幂律指数在0.8～1.1 范围内，Ca为0～0.15 范围内的结果大致相同[14]，液滴形成时间越短.这是因为随着Ca增加，主管道幂律流体的速度增大，黏性力所占的比重越大，子管道受到的剪切力越大，液体越容易变形，也即液体越容易破裂形成液滴，液滴的尺寸相应减小，形成液滴的时间变短.当幂律指数n＜1 时，液滴都呈挤压流型；当幂律指数n=1 时，液滴由挤压流型逐渐变为球状；当幂律指数n＞1 时，液滴由球状变为液滴状.

图8 主管道流体为剪切变稀流体(n=0.6)时，不同Ca 下的T 型微通道内液滴形成过程Fig.8 The droplet formation process in the T-junction microchannel obtained with different capillary numbers for a shear thinning continuous phase fluid (n=0.6)

图11 给出了不同幂律指数n时，主管道Ca对T 型微通道内液滴尺寸、形成时间以及变形参数的影响.从图中可以看出，液滴尺寸随着Ca的增加而减小，另一方面当Ca一定时，幂律指数越大，液滴尺寸越小，并且对于不同n的情况，液滴尺寸随Ca减小的速率基本是不变的(图11(a))，这也与前文中液滴尺寸和幂律指数之间的线性关系相对应.此外，随着Ca的增加，液滴的形成时间和变形参数先快速减小后缓慢减小(图11(b)和图11(c)).为了更详细地说明Ca对液滴的形成时间和变形参数的影响，我们分别选取图中一种剪切变稀(n=0.6)、Newton 和剪切变稠(n= 1.4)情况来看，当Ca从0.003 43 增加到0.006 87，n为0.6 时，液滴的形成时间从5.07 ms 减小到2.20 ms，液滴的变形参数从0.181 减小到0.116；当n为1.0 时，液滴的形成时间从3.65 ms减小为1.61 ms，液滴的变形参数从0.096 减小到0.063；当n为1.4 时，对应的液滴形成时间分别为2.79 ms和1.32 ms，液滴的变形参数分别为0.057 和0.038.从以上数据可知，当n为0.6，1.0 以及1.4 时，Ca从0.003 43增加到0.006 87，液滴的形成时间分别减少了56.6%，55.9%以及52.7%，而液滴的变形参数分别减小了35.9%，34.4%以及33.3%.可知，T 型微通道内液滴的形成时间与变形参数都随Ca的增加而减小，且减小趋势随幂律指数的增大而减小.

图9 主管道流体为Newton 流体(n=1.0)时，不同Ca 下的T 型微通道内液滴形成过程Fig.9 The droplet formation process in the T-junction microchannel obtained with different capillary numbers for a Newtonian continuous phase fluid (n=1.0)

图10 主管道流体为剪切变稠流体(n=1.4)时，不同Ca 下的T 型微通道内液滴形成过程Fig.10 The droplet formation process in the T-junction microchannel obtained with different capillary numbers for a shear thickening continuous phase fluid (n=1.4)

图11 主管道Ca 和幂律指数n 对液滴的影响：(a)尺寸；(b)形成时间；(c)变形参数Fig.11 The effects of continuous phase capillary number Ca and power-law index n on the droplet:(a) the size; (b) the formation time; (c) the deformation index

3.3 流量比Q 对液滴形成的影响

本小节研究主管道与子管道的流量比对液滴运动机理的影响，这里主要考虑了三种不同流量比的情况Q=6.25，8.33 和12.5.相似地，对于不同的流量比都研究了剪切变稀、Newton 和剪切变稠三种情况.数值模拟中Ca= 0.004 29，黏度比M= 1.98，主管道固体壁面为完全润湿性表面.

图12～14 分别给出了不同主管道和子管道流量比Q下，主管道幂律流体为剪切变稀、Newton 以及剪切变稠时得到的液滴形成过程图.从图中可以看出，无论主管道为剪切变稀(图12)、Newton (图13)以及剪切变稠(图14 )，都有流量比Q越大，形成的液滴尺寸越小，这与前人研究幂律指数变化范围较小，流量比范围较小情况下的结果大致相同[14]，液滴形成时间越长.这是因为流量比Q越大，子管道速度越小，子管道的惯性力就越小，抵抗主管道剪切应力越弱；随着幂律指数的增加，主管道的剪切力和黏滞力抑制了子管道的惯性力，因此在其他不变的情况下，形成的液滴尺寸越小.由于子管道的体积流量小，因此子管道被挤压破裂形成液滴时间就越长.

图12 主管道流体为剪切变稀流体(n=0.6)时，在不同流量比Q 得到的T 型微通道内液滴形成过程Fig.12 The droplet formation process in the T-junction microchannel obtained with different flow ratios Q for a shear thinning continuous phase fluid (n=0.6)

图13 主管道流体为Newton 流体(n=1.0)时，不同流量比Q 得到的T 型微通道内液滴形成过程Fig.13 The droplet formation process in the T-junction microchannel obtained with different flow ratios Q for a Newtonian continuous phase fluid (n=1.0)

图14 主管道流体为剪切变稠流体(n=1.4)时，不同流量比Q 得到的T 型微通道内液滴形成过程Fig.14 The droplet formation process in the T-junction microchannel obtained with different flow ratios Q for a shear thickening continuous phase fluid (n=1.4)

图15 给出了流量比Q和幂律指数n对T 型微通道内液滴尺寸、形成时间以及变形参数的影响.从图中结果可以发现，液滴尺寸随两相流量比的增加而减小，且流量比Q一定时，幂律指数n越大，形成的液滴尺寸越小，同样地，对于不同幂律指数的情况，减小速率基本保持不变(图15(a)).另外，随着流量比Q的增加，液滴形成时间变长，而液滴变形参数变小；并且流量比一定时，液滴的形成时间和变形参数都随幂律指数的增加而减小(图15(b)和图15(c)).同样地，为了说明不同幂律流体中液滴形成时间和变形参数随流量比的变化规律，在本小节中分别选取一种剪切变稀(n= 0.6)、Newton 和剪切变稠(n= 1.4)情况来定量分析.随着流量比Q从6.25 增加到12.5，当n为0.6 时，液滴形成时间从2.55 ms 增加到3.63 ms，液滴的变形参数从0.182 减小为0.117；当n为1.0 时，液滴形成时间从1.75 ms 增加到2.62 ms，液滴的变形参数从0.099 减小为0.04；当n为1.4 时，液滴形成时间从1.36 ms 增加到2.15 ms，液滴的变形参数从0.056 减小为0.035.由此可知，对于不同幂律指数n的情况，都有T 型微通道内液滴的形成时间随流量比的增加而增加，而变形参数随流量比的增加而减小.此外，n为0.6，1.0，1.4 时，流量比从6.25 到12.5，液滴形成时间分别增加了42.4%，49.7%，58.1%，液滴的变形参数分别减小了35.7%，59.6%，37.5%.综上所述，对于不同的幂律流体，液滴的形成时间随流量比的增加而增加，且增长速度随n的增加越来越快.另一方面，液滴的变形参数随流量比的增加近似线性减小，且减小速度随幂律指数的增加先增加后减小.

图15 流量比Q 和幂律指数n 对液滴的影响：(a)尺寸；(b)形成时间；(c)变形参数Fig.15 The effects of continuous phase flow ratio Q and power-law index n on the droplet: (a) the size; (b) the formation time; (c) the deformation index

3.4 黏度比M 对液滴形成的影响

本小节研究子管道和主管道流体的黏度比M对液滴运动机理的影响.主要研究了黏度比M分别为1.65，2.46 和2.8 对液滴形成时间、液滴尺寸大小以及液滴的变形参数的影响，每种情况同样都研究了剪切变稀、Newton 和剪切变稠三种情况.数值模拟中初始Ca=0.004 29，流量比Q=10，固体壁面为完全润湿性表面.

图16～18 分别给出了不同黏度比M的情况下，主管道幂律流体分别为剪切变稀(n= 0.8)、Newton 以及剪切变稠(n= 1.2)时液滴形成的过程图.从图中可以看出，无论主管道幂律流体为剪切变稀、Newton 以及剪切变稠，都有子管道与主管道流体的黏度比M越大，形成液滴尺寸越小，液滴形成时间越短.这是由于随着黏度比增大，主管道幂律流体运动黏度变小，使得液滴在幂律流体中更容易断裂[13-14].

图16 主管道流体为剪切变稀流体(n=0.8)时，不同M 得到的T 型微通道内液滴形成过程Fig.16 The droplet formation process in the T-junction microchannel obtained with different viscosity ratios M for a shear thinning continuous phase fluid (n=0.8)

图19 给出了不同黏度比M和幂律指数n对T 型微通道内液滴尺寸、形成时间以及变形参数的影响.由图可知，液滴尺寸、形成时间以及变形参数都随M和n的增加而减小，且减小速度近似不变.另一方面，随着M和n的增加，液滴的形成时间和变形参数减小 (图19(b)和图19(c)).当黏度比M从1.65 变化到2.8 时，当n=0.6 时，液滴的形成时间从4.81 ms 减小到2.47 ms，液滴变形参数从0.177 减小到0.137；当n为0.8 时，液滴的形成时间从4.13 ms 减小到2.15 ms，液滴变形参数从0.131 减小到0.094；当n为1.0 时，液滴的形成时间从3.46 ms 减小到1.84 ms，液滴变形参数从0.094 变化到0.057；当n为1.2 时，液滴形成时间从2.94 ms 减小到1.63 ms，液滴变形参数从0.054 变化到0.033；当n为1.6 时，液滴形成时间从2.52 ms 减小到1.46 ms，液滴变形参数从0.039 变化到0.03.综上，当n为0.8，1.0，1.2 时，M从1.65 到2.8，液滴的形成时间的分别减小了48.6%，47.9%，46.8%，44.6%，42.1%；液滴的变形参数分别减小了22.6%，28.2%，39.4%，38.9%，23.1%.可知，T 型微通道内液滴的形成时间随黏度比的增加而减小，且减小趋势随幂律指数的增加而减缓；液滴变形参数随黏度比的增加而减小，且变化趋势随幂律指数的增加先变大后变小.此外，对比图19 和图7 可知，黏度比对液滴形成尺寸、形成时间以及变形参数的影响规律与幂律流体的影响规律基本一致.

图17 主管道流体为Newton 流体(n=1.0)时，不同M 得到的T 型微通道内液滴形成过程Fig.17 The droplet formation process in the T-junction microchannel obtained with different viscosity ratios M for a Newtonian continuous phase fluid (n=1.0)

图18 主管道流体为剪切变稠流体(n=1.2)时，不同M 得到的T 型微通道内液滴形成过程Fig.18 The droplet formation process in the T-junction microchannel obtained with different viscosity ratios M for a shear thickening continuous phase fluid (n=1.2)

图19 黏度比M 和幂律指数n 对液滴的影响：(a)尺寸；(b)形成时间；(c)变形参数Fig.19 The effects of continuous phase viscosity ratio M and power-law index n on the droplet: (a) the size; (b) the formation time; (c) the deformation index

3.5 主管道壁面润湿性θ 对液滴形成的影响

本小节主要研究主管道壁面润湿性θ 对液滴形成的影响，主要考虑了三种润湿性情况：θ=60°，90°，120°.对于不同壁面润湿性θ 都分别研究了剪切变稀、Newton 和剪切变稠时液滴的尺寸、形成时间和变形参数.数值模拟中固定Ca=0.004 29，黏度比M=1.98，流量比Q=10.0.

图20～22 分别给出了主管道幂律流体为剪切变稀、Newton 以及剪切变稠流体时在不同主管道内壁面润湿性情况下得到的液滴形成过程图.如图所示，当内壁面润湿性具有亲水性时，形成的液滴会附着在壁面上，随着壁面润湿性的增加，液滴的形状逐渐改变，最终变为塞状，这一现象与液滴Newton 流体中形成的结论相同[7].无论主管道为剪切变稀、Newton 以及剪切变稠流体，在同一幂律指数n下，都有主管道固壁面润湿性θ 越大，形成的液滴尺寸越小；液滴形成时间越短；在同一润湿性下，幂律指数n越大，液滴尺寸越小.这是因为固体壁面接触角润湿性θ 越大，内壁面润湿性亲气性越强，亲水性越弱，则液体受到固体壁面的黏附力越小，因此，形成的液滴越小，对应的液滴形成时间越短.

图20 主管道流体为剪切变稀(n=0.8)时，不同壁面润湿性θ 得到的T 型微通道内液滴形成过程Fig.20 The droplet formation process in the T-junction microchannel obtained with different surface wettabilities θ for a shear thinning continuous phase fluid (n=0.8)

图21 主管道流体为Newton 流体(n=1.0)时，不同壁面润湿性θ 得到的T 型微通道内液滴形成过程Fig.21 The droplet formation process in the T-junction microchannel obtained with different surface wettabilities θ for a Newtonian continuous phase fluid (n=1.0)

图22 主管道流体为剪切变稠流体(n=1.2)时，不同壁面润湿性得到的T 型微通道内液滴形成过程Fig.22 The droplet formation process in the T-junction microchannel obtained with different surface wettabilities θ for a shear thickening continuous phase fluid (n=1.2)

图23 给出了不同幂律指数n时主管道壁面润湿性θ 对T 型微通道内液滴尺寸、形成时间以及变形参数的影响.这里需要指出的是，由于在亲水条件下，液滴吸附在主管道壁面上，并未形成椭圆状的液滴，而本文的变形参数是建立在液滴呈椭圆状的基础上，因此在本小节中，用Lc/W0变化代替液滴的变形参数.由图23 结果可知，形成的液滴尺寸随壁面润湿性θ 的增加近似呈线性减少，并且对于不同幂律指数的情况，液滴尺寸减小速率基本保持不变.液滴的形成时间同样随幂律指数的增加而减少(图23(b)).由图23(c)可知，液滴的变形参数随壁面润湿性θ 的增加，先快速减小然后缓慢减小.接下来我们分别选取一种剪切变稀(n=0.8)、Newton 和剪切变稠(n=1.2)流体进一步说明液滴形成时间和变形参数和润湿性之前的关系.当n为0.8 时，θ 从60°到150°，液滴的形成时间从3.82 ms 减小到3.45 ms，液滴的变形参数从1.867 减少到0.95；当n为1.0 时，液滴形成时间从3.15 ms 减小到2.91 ms，液滴的变形参数从1.433 减小到0.823；当n为1.2 时，θ 从60°到150°，液滴形成时间从2.73 ms 减小到2.54 ms，液滴变形参数从1.1 减少到0.664.综上，当n为0.8，1.0，1.2 时，θ 从60°到150°，液滴形成时间分别减小了9.7%，7.6%，7.0%，液滴变形参数分别减少了49.1%，42.7%，39.6%.由以上结果可知，T 型微通道内液滴的形成时间和变形参数随着润湿性的增加而减小，且减小趋势随幂律指数的增加而减缓.需要指出的是，尽管这里只选取了三种n的情况，以上结论对于其他n的情况也同样成立.

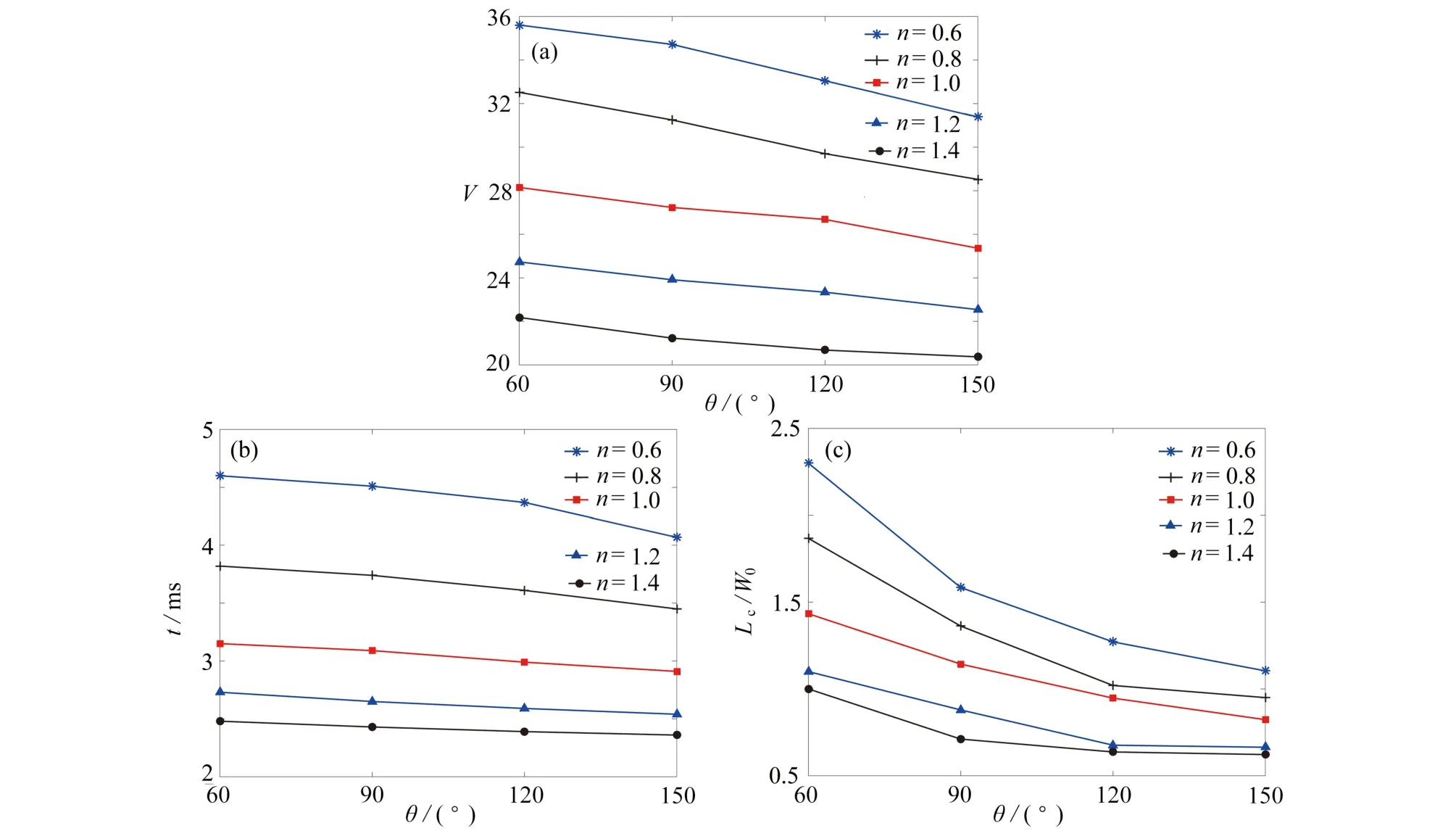
图23 润湿性θ 和幂律指数n 对液滴的影响：(a)尺寸；(b)形成时间；(c)相对长度Fig.23 The effects of continuous phase surface wettability θ and power-law index n on the droplet:(a) the size; (b) the formation time; (c) the deformation index

4 结 论

本文采用非Newton 不可压缩两相流格子Boltzmann 模型，研究了流体幂律指数n、毛细数Ca、两相流量比Q、两相黏度比M以及主管道内壁面润湿性θ 对液滴在T 型微通道内的形成尺寸、形成时间和变形参数(DI)的影响，得到了以下结论：

1) 幂律指数和黏度比对液滴的形成尺寸、形成时间以及变形参数的影响基本一致，即随着幂律指数和黏度比的增加，液滴的形成尺寸近似线性减小，而液滴的形成时间和变形参数先快速减小然后缓慢减小.

2) 壁面润湿性和Ca对液滴的形成过程的影响基本一致，即液滴的形成尺寸随Ca和壁面润湿性的增加而线性减少；而液滴的形成时间和液滴变形参数随Ca和壁面润湿性的增加而减小，且减小趋势随幂律指数的增加而减缓.

3) 流量比越大，液滴的形成尺寸和变形参数越小，而液滴的形成时间越长.