基于加窗插值和ZoomFFT 的电网宽频信号自适应测量方法

彭佳伟，潘树国，高 旺，沈 健，张 敏

（1. 东南大学仪器科学与工程学院,江苏省 南京市 210096；2. 南瑞集团有限公司（国网电力科学研究院有限公司）,江苏省 南京市 211106；3. 智能电网保护和运行控制国家重点实验室,江苏省 南京市 211106）

0 引言

近年来,随着可再生能源的开发普及和智能电网的持续发展,电力系统呈现出复杂互联和高度电力电子化的发展趋势。传统电力设备逐渐被各种集成化和智能化的电力电子设备代替,增强了电力系统的控制和运行维护能力［1-3］,但同时也带来了诸多问题,其向电网引入了大量间谐波及高次谐波等宽频信号,恶化了电能质量,导致电力系统和设备运行维护复杂化且风险增大［4-6］。

准确地测量电网信号中各成分分量是电力系统安全稳定运行的重要保障。为此,国际电工委员会（IEC）发布的IEC 61000 系列技术报告和标准中对50 次以内电力谐波的相关指标进行了分析和限定［7］,然而现有的电力系统测量装置和算法多针对工频及20 次以内谐波的测量,无法全面监测0～2.5 kHz 范围内的电力信号［8］。此外,在电网信号呈现出高频化发展趋势的同时,应用广泛的电力电子装置和负载设备向系统中引入了大量谐波和间谐波。多数测量装置的频率分辨率仅达5 Hz［9］,测量算法也局限于工频及谐波信号测量,缺乏面向宽频信号的自适应测量算法,难以满足宽频信号测量的分辨率要求——间隔为1 Hz 的间谐波或0.1 Hz 数量级的振荡信号等。综上可知,电力系统中现有的测量装置与技术难以满足电力电子化电网的宽频信号测量需求。

谐波和间谐波的测量方法可大致分为3 类:时频域方法、谱估计测量方法和机器学习方法。在时频域方法中,快速傅里叶变换（FFT）、小波变换［10］和希尔伯特-黄变换［11］最具代表性。其中,FFT 具有计算量小、易于工程实现等优点,使其成为电力系统运行维护中最常用的频谱分析方法,但其受栅栏效应和谱线干扰等问题的影响。对此,相关学者提出了谱线插值校正和复调制细化谱分析,即选带傅里叶变换（ZoomFFT）等改进方法［12-13］,但在频率分辨率方面仍存在不足。基于小波变换、希尔伯特-黄变换的方法尽管能够实现较高的分辨率和非线性、非平稳信号的分析,但算法须进行相应预设且实时性较差,难以实际应用于电力系统测量装置。而在谱估计测量方法中,基于多重信号分类法［14］和旋转不变参数估计法［15-16］的算法均具有超分辨率的特性,但仅限于中低频段测量且精度易受噪声影响。机器学习方法如遗传算法［17］和支持向量机［18］等有着自适应性强和精度高的特点,但其多基于在线训练,存在运算复杂和难以独立测量的缺陷。

为了满足高精度、高分辨率的宽频信号测量需求,本文分析了傅里叶变换类的时频测量方法。其中,加窗插值校正的方法具有运算量小、精度稳定等优点。然而,当插值校正利用的谱线受到干扰时,分析精度会大幅降低。此外,在符合IEC 标准［19］的情况下,难以有效测量频率相近的谐波及间谐波。而ZoomFFT 能以较高的分辨率对特定频率范围进行频域分析,实现频率相近信号分量的测量,但难以实现0～2.5 kHz 宽频范围内的全面测量。为此,本文结合加窗插值校正和ZoomFFT 算法,在选取窗函数后基于谱线的相位特性进行主瓣干扰的判定,根据判定结果采用不同算法进行分析,进而在宽频范围内实现了信号自适应测量。最后,通过仿真对比及实测数据分析验证了本文测量方法的有效性、测量精度和工程可实现性。

1 主瓣干扰及其判定

1.1 相近频率分量间的主瓣干扰

假设存在某一含有频率分量f1和f2的电网信号（多频率分量的推广同理）,其加窗后的频谱分析结果如图1 所示。

图1 加窗后的主瓣干扰Fig.1 Main-lobe interference after windowing

从图1 可以看出,f1和f2相差越小,其频谱将产生以复数叠加的混叠,且程度从旁瓣到主瓣越来越深。虽然加窗能够抑制旁瓣,但当2 个频率分量的主瓣部分产生混叠时,则会产生主瓣干扰现象。主瓣干扰使得2 个频率分量的谱线幅值严重失真,此时采用谱线插值法校正FFT 结果将产生较大误差。因此,在采用加窗FFT 进行信号分析时,须首先判断某一频谱处是否存在谱线干扰,再针对性地采取不同算法进行处理。

1.2 主瓣干扰的判定

一般可基于主瓣内谱线的相位或幅值特性判断频谱中是否产生了主瓣干扰。当主瓣中的谱线未受到其他频率分量的影响时,主瓣内相邻谱线间的相位差的绝对值应为π。

由于不同窗函数的主瓣宽度不同,判定时采用的谱线个数也不同。序列长度为N的窗函数的主瓣宽度可表示为2πk/N,即主瓣中最多含有k条谱线,此时可利用靠近频谱顶部的k-1 条谱线进行判定。但当主瓣较窄时,位于边缘处的谱线易受到噪声的影响,导致误判。因此,可通过采用主瓣较宽的窗函数主瓣中靠近峰顶的k-3 条谱线判断是否存在主瓣干扰。

考虑到频谱泄漏、计算误差和噪声的影响,本文将相邻谱线间各相位差与π 之差的最大值与阈值ε相比,以判断是否存在主瓣干扰。令相邻谱线间相位差与π 的差为Δφj,此时有:

显然ε的取值直接影响本文算法的自适应性,取值较小会导致主瓣干扰的误判,而取值较大则会造成漏判,使得信号参数无法得到有效估计而导致方法失效。本文对不同信噪比下的不同幅值比和频率差的信号分量进行仿真遍历,在谱线插值法无法有效进行参数估计的信号分量（如频率相近或低幅值分量）能被有效识别的前提下,尽可能避免引入不必要的运算量,进而将阈值设定为ε=1.4。

采用谱线幅值特性进行主瓣干扰判定的过程会将插值校正的过程提前,当信号相对“整洁”、不存在频率相近的间谐波分量时,则会引入不必要的计算代价,且基于相位差的判定方法可靠性较强,故本文基于谱线的相位特性进行主瓣干扰的判定。

2 余弦窗谱线插值校正算法

当某一频谱处不存在主瓣干扰时,可认为在频域内的此处仅存在一个频率分量,则对加窗后的结果进行谱线插值校正。而不同的窗函数插值校正过程不同,因此需要对窗函数进行对比选取。

2.1 窗函数选取

余弦窗函数时域表达式为:

在实际情况下,基于傅里叶变换的方法难以实现同步采样。此时,采用旁瓣峰值电平小且衰减速率大的窗函数,不仅能够抑制非同步采样造成的频谱泄漏,还能减少相近频率分量对谐波分析的干扰。因此,应侧重于选取旁瓣性能优异的窗函数。

在降低栅栏效应方面,一般可通过谱线插值对结果进行校正。为了保证插值校正的频率分量不存在谱线干扰,即充分避免额外引入影响校正精度的因素,应避免采用主瓣宽度过窄的窗函数。较宽的主瓣会使得主瓣干扰更早出现,这样能使相近的各频率分量得到针对性处理,进而确保信号测量精度。因此,应侧重于选取主瓣相对较宽的窗函数,但不宜过宽。此外,窗函数主瓣宽度与旁瓣大小和衰减速度存在着“此消彼长”的关系,这就刚好和更优旁瓣性能的选取标准相契合,将旁瓣性能越优导致主瓣越宽的这一负面代价,转化成改善信号参数估计精度的正面增益。然而,尽管窗函数项数越多,其旁瓣性能越好,但项数的增加还会一定程度上导致插值校正算法复杂化。

综上,本文拟从表1 所列的4 项系数余弦窗中选取窗函数对电网信号进行处理,各窗系数见附录A表A1。

2.2 双谱线插值校正算法

本文测量方法中的插值校正算法仅用于未发生主瓣干扰的频谱分析,相比多谱线插值和频移校正法［20-21］,计算量较少的双谱线插值已能够充分满足精度需求。

设某含有M个频率分量的信号表达式为:

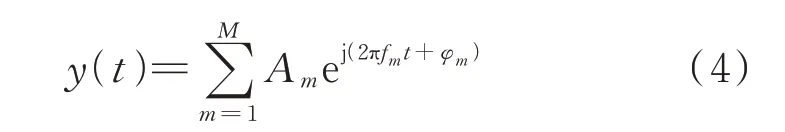
式中:Am、fm、φm分别为第m个信号分量的幅值、频率和相位。

对以采样频率fs进行采样后得到的序列加4 项余弦窗后的离散傅里叶变换结果为:

式中:i为插值系数δm的次数；bi和c2i均为余弦窗系数ah的多项式函数,各多项式系数见附录A 表A2。

其中各4 项余弦窗中仅4 项5 阶Nuttall 窗的谱线幅值比βm中的bi和c2i（i≠0）均为0,即可得到插值系数δm关于幅值比βm更易于工程实现的显式表达式,进而可根据δm对频谱分析结果进行校正,此时有:

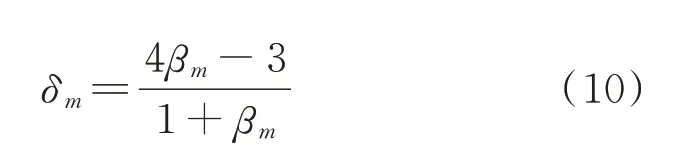
其余余弦窗函数对应的βm均为关于δm的高次方程,但此时βm很难存在反函数。即使存在,对其的求取也较为复杂。若不求取βm的反函数表达式,也需要根据式（9）对每个βm求取δm在[0,1)范围内的解,计算量大且过程烦琐。因此,这类插值系数非显式表达式的余弦窗插值校正过程多采用幅值比β=(|X(km+1)|-|X(km)|)(|X(km+1)|+|X(km)|)-1的方法［22-23］,但也需要通过多次拟合求得插值系数关于幅值比的多项式,计算复杂的同时又会带来无法避免的模型误差。

综合考虑各4 项系数窗函数的旁瓣性质和插值校正过程,本文采用基于4 项5 阶Nuttall 窗的双谱线插值校正算法对不存在主瓣干扰的频率分量进行参数估计,频率、幅值和相位的校正公式为:

通过式（11）至式（13）即可得到信号的频率、幅值和相位参数。

3 复调制细化谱分析法

当某一频谱处存在主瓣干扰时,则认为此处存在多个频率分量,此时须采用分辨率更高的信号测量算法对混叠频谱进行处理,其中ZoomFFT 就是具有“选带”分析能力的算法。

ZoomFFT 算法能够实现信号频域的局部细化放大,使特定频带获得较高的频率分辨率,一般采用频移法实现,其具体步骤为:

1）对信号y(t)进行加窗采样后,对得到的长度为DN的采样序列乘以单位旋转因子e-j2πnfm/fs进行复调制移频,形成了一个以fm为频率零点的新信号y′(n),其中D为细化倍数。

2）对y′(n)进行FFT 后,进行低通数字滤波,去除信号须细化频带外的频率成分,以避免后续重采样时产生频谱混叠。

3）对滤波后的数据进行长度为DN的快速傅里叶逆变换（IFFT）得到时域序列后,进行重采样,采样间隔为D,采样频率变为fs/D。

4）对重采样后得到的N点时域序列进行FFT并移至实际频率处,此时频率分辨率为(fs/D)/N=fs/(DN),即频率分辨率提高了D倍。

根据重新排列得到的FFT 结果,即可得到原信号序列在以频率fm为中心、细化频率范围fs/D内的频谱特性,实现细化放大。

ZoomFFT 算法的效果主要在于细化倍数的设置。若设置过高,会造成算法需要基于长采样序列,且低通滤波器的过渡带宽度对精度的影响增大；设置过低又会导致算法无法以理想的频率分辨率有效分析存在主瓣干扰的频谱。此外,由于宽频测量时信号采样频率较高,导致细化频带范围较大,容易将不存在主瓣干扰的频谱再次进行分析计算,造成运算和内存资源的浪费。针对这一矛盾,可在细化倍数较大时,设置信号采样长度为DN/P,P∈N+,并对算法的幅值结果乘以P以恢复为真实幅值。这样就能以较为适中的算法实时性、计算量和内存代价,保证算法的分辨率、估计精度以及针对性更强的细化频带。

综上所述,主瓣干扰的判定、4 项5 阶Nuttall 窗谱线插值算法和ZoomFFT 算法形成本文测量方法,如图2 所示。

图2 电网宽频信号的自适应测量流程Fig.2 Flow chart of adaptive measurement for wideband power grid signal

4 仿真验证与分析

4.1 复杂电网信号仿真验证

由于本文方法主要应用于电网宽频信号的自适应测量,因此须在确保算法实时性的前提下,实现频率相近间谐波和高次谐波的高精度测量。结合实际电网信号的特点,设定某含有基波、各次谐波和间谐波的电网信号信噪比为60 dB,参数设定如表2所示。

表2 仿真参数Table 2 Simulation parameters

由于宽频信号最高频率至少可达2.5 kHz,则根据Nyquist 频率避免频率混叠,同时考虑到同步相量测量装置的录波采样频率,此时设定仿真采样频率fs=6.4 kHz,根据IEC 标准［19］设置采样信号频谱分析时间窗为10 个基波周期,即采样点数N≈1 280。ZoomFFT 的细化倍数D=50,其采样点数NZFFT=12 800。

鉴于幅值较低的信号分量易受到背景噪声或其他信号分量频谱泄漏的影响而出现主瓣干扰,本文对该信号进行仿真并在测量100 次后对测量结果取平均值,以保证仿真结果的可靠性。仿真结果如图3 所示,其中误差大小为各信号分量参数的误差标准差,即±σ,用于表明该测量方法的精度稳定性。

由图3 可以看出,本文方法有效实现了信号的自适应测量,其中ZoomFFT 算法针对基波及其附近间谐波以及频率差仅为1 Hz 的间谐波参数进行了估计,基于4 项5 阶Nuttall 窗的双谱线插值校正算法则测量了未产生主瓣干扰的谐波分量。此外,虽然35 次和49 次谐波附近均不存在其他信号分量,但较低的幅值使其易受到频谱泄漏和背景噪声的影响而产生主瓣干扰。因此,在仿真过程中2 种算法均进行过该分量的参数估计。

图3 频率、幅值和相位估计结果及相对误差Fig.3 Estimation results of frequency,amplitude and phase and relative errors

ZoomFFT 算法的整体测量结果相较于基于4 项5 阶Nuttall 窗的双谱线插值校正算法更为稳定、误差波动较小、频率估计精度更高,实现了对频率参数的准确估计,但幅值估计精度稍低于后者,这也导致高次谐波的参数估计误差波动较大,而在相位估计精度方面,2 种算法基本相当。

此外,根据图3 中误差可以看出,测量方法整体精度较高、稳定性好,频率相对误差低于7×10-5,幅值误差数量级在10-4～10-3,相位误差相对较大,但也不超过1.6×10-2。

4.2 与常规方法的对比仿真验证

为对比分析,对上述复杂电网信号分别采用Hamming 窗、3 项3 阶Nuttall 窗、4 项3 阶Nuttall 窗、4 项5 阶Nuttall 窗、ZoomFFT 和本文测量方法进行测量,其中4 种加窗算法均采用双谱线插值对结果进行校正,Hamming 窗和4 项3 阶Nuttall 窗的插值校正公式无显式表达式,均通过拟合得到。同样进行100 次仿真后对测量结果取平均值,其算法运行代价、在CPU 上单次平均运行时长和信号参数估计精度如表3 和图4 所示,具体结果见附录B 表B1 至表B6。其中,“测量情况”表示某方法是否将该信号中的所有信号分量有效分辨和测量。

表3 各方法测量结果及运行代价Table 3 Measurement results and operation cost of each method

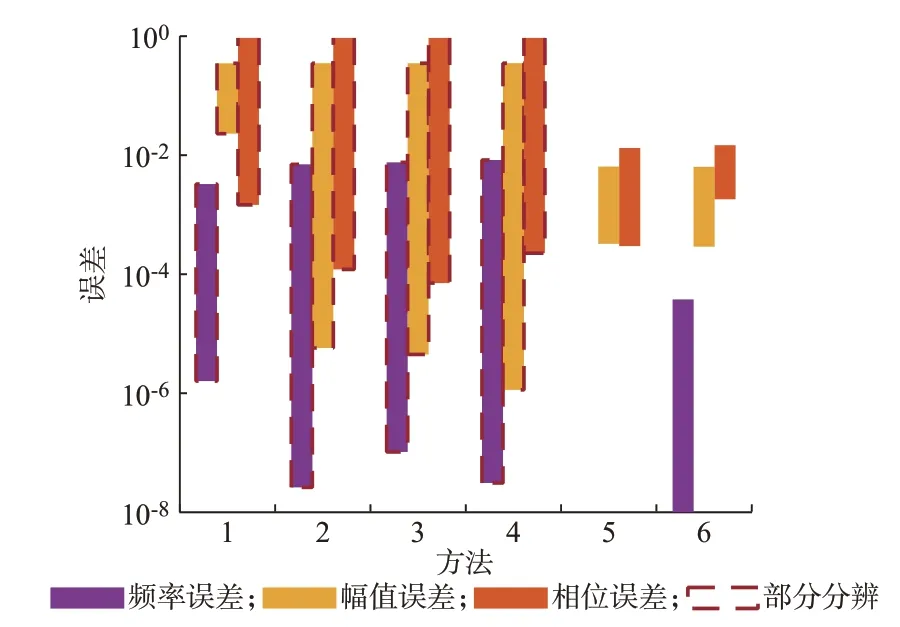
图4 各方法测量误差范围Fig.4 Measurement error range of each method

从表3 可以看出,4 种加窗谱线插值校正算法的运算代价相比ZoomFFT 和本文方法更小,其中Hamming 窗和4 项3 阶Nuttall 窗的时长稍长于另2 个窗函数的原因是其插值校正公式均为拟合得到,运算量较大。

在所测频率分量不存在主瓣干扰时,这4 种加窗谱线插值校正算法的频率估计精度均高于另2 种算法的参数估计精度。其中,尽管Hamming 窗和3 项3 阶Nuttall 窗旁瓣性能较差,但此时其更窄的主瓣带来的分辨率增益一定程度上保证了二者的频率估计精度。然而在存在主瓣干扰时,由于无法以高精度算法减少频谱泄漏等因素的影响,这4 种方法均无法分辨出频率为45 Hz 和116 Hz 的间谐波分量,进而导致频率与之相近的信号分量参数估计精度偏低,部分幅值及相位估计结果完全不可靠。

ZoomFFT 有效分辨出了所有信号分量且准确测量出了各频率值,整体精度最高,但所需采样点数最多且由于要重复运行以遍历待测频率上限内的所有信号分量,其运行时长最长,实用性偏低,即使将放大倍数降低1/2（D=25）,即细化范围增大一倍后,运行时长达到15 ms,仍远大于本文方法。

虽然本文测量方法的复杂度稍高于同样有效估计出所有参数的ZoomFFT 算法,但在判断主瓣干扰时,式（1）计算过程中的谱线相位结果可再次用于插值校正进行式（13）的相位估计。其自适应特性在有效结合2 种算法优点的同时,弥补了加窗插值无法分析频率相近的信号分量和ZoomFFT 在宽频测量时须大范围遍历的不足,使得运行时长远低于ZoomFFT 算法,且当信号中不含频率相近的间谐波分量或低幅高次谐波,即不存在主瓣干扰时,信号测量完全由基于4 项5 阶Nuttall 窗的双谱线插值校正算法实现,此时采样点数与常规加窗插值校正算法相同,计算量小、实时性高,运行代价相较于ZoomFFT 的遍历测量降低了近2 个数量级。

不难看出,本文测量方法能以高分辨率实现复杂电网宽频信号的自适应测量,在避免了不必要的计算代价、减少了运算量和测量耗时的同时,保证了测量精度和实时性,具有实际应用价值,适合在嵌入式等硬件平台系统上进行电网信号的实时测量。

5 实测数据验证

利用本文测量方法对中车风电后水泉风电场的220 kV 母线电压录波数据（见附录B 图B1）进行分析,电压变比为220 kV/100 V,录波数据由安装部署于现场的同步相量测量装置（SMU-2ME）连续录波得到,采样频率为6.4 kHz,方法初期数据长度为1 280,若存在主瓣干扰则数据长度增加至12 800 以满足ZoomFFT 运行需要,主瓣干扰判定阈值仍为1.4,参数估计结果如附录B 表B7 所示。

由结果可以看出,本文测量方法有效估计出了各信号参数。在频率方面,该电压信号基频无频率偏移且不存在间谐波,但信号中存在最高达13 次的多个低幅谐波分量。在幅值方面,基频相电压均值为57.734 V,对应的线电压为99.998 V,符合实际电压变比大小,幅值估计精度较高。此外,三相间存在一定程度的不平衡,如仅在A 相和B 相中存在13 次谐波,这类谐波在其他相中可能不存在或幅值低于0.1 V。在相位方面,此时利用各相间相位差是否为120°对相位估计结果进行验证:

式中:φA、φB、φC分别为A、B、C 相相位；θA、θB、θC分别为A、B、C 相相位偏差。

此时三相中均稳定存在的谐波分量的相位估计结果及其绝对相位偏差的均值如表4 所示。

表4 相位估计结果及绝对相位偏差的均值Table 4 Phase estimation results and average value of absolute phase deviation

由表4 可以看出,该电压信号中三相相位较为平衡,其中工频各相间相位差基本为120°。在实际情况下电网信号中的奇次谐波一般存在一定程度的三相不平衡情况,不平衡程度与谐波源、幅值大小等因素相关,此时若假设方法误差受分量幅值高低影响而围绕某固定值小幅波动,则可以看出各次谐波的不平衡度与实际情况相符。综上,可在一定程度上认为本文测量方法实现了较高精度的相位估计。

6 结语

针对电网信号复杂化、宽频化发展趋势下的高精度测量需求,本文提出一种面向电网宽频信号的自适应测量方法。利用信号频谱的相位特性判断其中是否存在主瓣干扰,根据判别结果针对性地采用计算量小、满足谐波高精度测量的4 项5 阶Nuttall窗双谱线插值校正算法,以及分辨率更高、满足频率相近间谐波及低幅高次谐波高精度测量的ZoomFFT 算法。通过仿真对比及实测录波数据分析验证了本文方法的性能:1）实现了复杂宽频信号的高精度自适应测量,稳定且有效估计出了频率差仅为1 Hz 的间谐波和低幅高次谐波的参数；2）有效结合了2 种算法的优点,测量精度高于常见加窗双谱线插值校正算法的同时,运行代价及计算量又远低于ZoomFFT 算法,适合实际工程应用。

需要说明的是,尽管本文所提测量方法的频率分辨率能够满足大部分复杂谐波及间谐波的测量,但当频率差在10-1数量级时,如频率主要位于0.1～2.5 Hz 的低频振荡,则须进一步提高测量方法自适应性并结合分辨率更高的测量算法。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。