考虑频率二次跌落的系统频率特征评估及风电调频参数整定

张雯欣，吴 琛，黄 伟，高晖胜，程 旻，辛焕海，

（1. 浙江大学工程师学院,浙江省 杭州市 310027；2. 云南电网有限责任公司,云南省 昆明市 650011；3. 浙江大学电气工程学院,浙江省 杭州市 310027）

0 引言

近年来,风光等新能源在电力系统中的渗透率不断提高。新能源一般运行于最大功率点跟踪（MPPT）模式而不参与调频,这降低了系统惯性,弱化了系统调频能力,给系统频率稳定带来不利影响。

国内外学者提出多种新能源主动参与调频的控制策略以提升系统频率稳定性［1-3］。对于风电机组,其通常经变流器并网,转子转速与电网频率解耦。为利用风电机组转子动能支撑频率,需要进行额外的调频控制,如虚拟惯量控制、下垂控制、虚拟惯量加下垂控制（简称为“惯量下垂控制”）与虚拟同步机技术等［4-6］。采用以上控制后,风电机组能在系统频率跌落时释放转子动能,提供有功支撑。而由于转速限制,风电机组无法持续增发有功功率。其退出调频时不再释放动能,反而需要从电网吸收功率以提高转速,这可能导致频率二次跌落［7-8］。目前,综合考虑系统频率一次跌落与二次跌落过程中的频率特征对风电调频参数进行整定的研究较少［9-10］。若只以提升一次跌落最低点为目标进行调频参数整定,则风电机组在频率一次跌落过程中将为系统提供大量有功支撑,但相应地,在恢复转速时需要吸收更多能量,进一步降低了二次跌落最低点［9］。若只以避免频率二次跌落为目标进行调频参数整定,则风电机组在频率一次跌落过程中被限制了有功支撑,避免了频率二次跌落,但是频率一次跌落最低点并未得到很好提升［10］。因此,为更好地支撑系统频率,满足系统实际的调频需求,需综合考虑包括一次、二次跌落在内的整个频率动态过程,对频率特征进行量化评估。为分析系统频率响应需要结合所有发电设备的模型,但全部采用详细模型会因系统阶数过高而难以分析［11］。因此,首先需要对设备的模型进行简化。

许多文献提出了多种发电设备的简化模型以研究系统频率动态［12-16］。例如,文献［14］在研究新能源高渗透的电力系统频率特性时基于简化聚合频率模型建立指标以分析频率,简化模型时须假设各种发电机具有相同的一阶惯性环节时间常数,但在实际多机系统中难以选出合适的一阶惯性环节时间常数确保所解析频率的精度最高。文献［15］在研究风电机组参与调频后频率二次跌落过程时也基于发电机简化模型进行分析,但该简化模型没有考虑系统实际发电机中的延时等环节,得出的参数较为粗略,无法准确描述频率特性,且无法简化多机系统中频率轨迹的计算。为解析频率特征,文献［16］提出使用一种由比例-积分-微分（PID）环节组成的传递函数结构来近似各设备的频率-有功功率响应。该模型结构中参数具有“模态性”,即需要依据系统的模态频率响应才能计算得到各设备调频能力的有效值。但这种传递函数结构只能分析扰动后较短时间内的频率动态,不适用于分析频率二次跌落过程。

为量化评估一次、二次跌落过程中的频率特征,改善系统频率响应,本文提出使用微分、比例及一阶滞后环节组成的统一结构来近似风电机组等各种发电设备频率-功率特性。基于统一结构模型解析系统频率响应量化评估一次、二次跌落最低点以及频率变化率等频率特征。进一步,以提升一次跌落最低点为优化目标,以二次跌落最低点不低于一次跌落最低点为约束,建立参数优化问题,整定风电机组惯量下垂控制参数。最后,通过仿真验证了上述频率特征评估方法及参数整定方法的有效性。

1 发电设备的统一结构简化模型

1.1 同步机与风电机组频率-功率动态特性分析

为简化分析,本文仅针对电力系统的总体频率特性［14］（即各节点频率响应中一致的部分,称为系统共模频率［16］）进行研究,并忽略电压波动以及调速系统死区等非线性对频率响应的影响。

基于以上假设,可结合系统中各发电设备得到系统共模频率响应为:

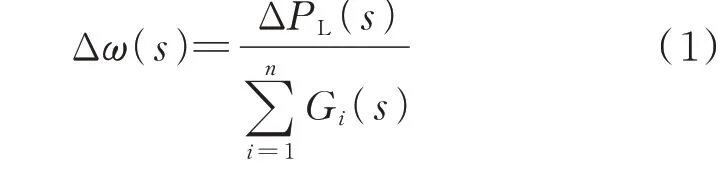
式中:Gi(s)为第i台发电设备频率-功率传递函数；ΔPL(s)为功率扰动量；Δω（s）为系统共模频率响应,本文规定负的扰动引起频率跌落；n为系统可参与调频发电设备数量（若要考虑负荷等设备的动态响应,将其视为特殊的发电机即可）。

同步机的调频动态可由转子运动方程描述,即

式中:J为转动惯量；GT（s）为调速系统频率-功率传递函数,通常可用一阶滞后环节近似［17］；D为阻尼系数；ΔPe(s)为同步机发出的电磁功率。

由式（3）可以得到传统同步机的频率-功率传递函数为:

本文考虑的风电机组为双馈风电机组,其控制结构见附录A 图A1,频率-功率传递函数见附录B［18］。对于直驱风电机组或其余类型的新能源设备,也可根据其模型写出频率-功率传递函数［18-19］,并采用本文方法进行分析。

如附录A 图A1 所示,风电机组正常运行时处于MPPT 模式,发出电磁功率Pw与输入机械功率Pm平衡；参与调频时采用惯量下垂控制,电磁功率增量与系统频率有关［8,15,18］；假设恢复转速时采用恒定输出电磁功率恢复转速策略［15］,后文2.1 节将对此进行详细解释。

由式（1）可知,多机系统的频率响应需结合所有发电设备的模型得到,但考虑各设备的详细模型时会因阶数过高而难以解析。因此,需要对各种设备的模型进行简化。为此,使用一种低阶的传递函数结构来近似各种发电设备。一方面,该传递函数结构保证了频率轨迹拟合的精度；另一方面,其能在求解频率响应时将系统简化为二阶系统,降低频率特征解析难度,并能得到相应经验公式简化频率特征量化结果。

1.2 统一结构模型选择

考虑到功率阶跃扰动下电力系统共模频率响应轨迹的一般变化规律（即频率响应一般存在超调量,且在稳态下存在静差,如图1 红色实线所示）,本文使用由微分-比例-一阶滞后3 个环节组成的统一结构等值各种设备的频率-功率响应模型,其表达式G(s)为:

图1 阶跃功率扰动下频率响应轨迹Fig.1 Frequency response trajectory with step power disturbance

式中:Ju、Du、Ku分别为有效惯量、有效阻尼系数及有效静态调差系数；T0为调差时间常数。

将式（5）进行拉普拉斯反变换,得到频率轨迹如图1 蓝色虚线所示。

值得一提的是,文献［16］用PID 环节来近似不同发电设备的频率-功率响应并获得近似的频率轨迹,如图1 绿色虚线所示。由于积分环节的无差调节特性,使得这种频率轨迹只能近似原轨迹到最低点周围这一段,在最低点之后的轨迹误差较大。而风电机组参与调频存在二次跌落现象,需要分析更长一段时间内的频率轨迹,因此,这种PID 结构无法用于研究风电导致的频率二次跌落现象。

相比于文献［16］中PID 统一结构,采用式（4）所示的微分-比例-一阶滞后环节统一结构近似各发电设备,可使所得到的系统频率响应在更长时间范围内与原模型几乎一致,上述分析从频率轨迹的角度说明了所选取统一结构模型的合理性及可行性。

为便于理解本文提到的统一结构与文献［16］中PID 统一结构的区别,对这两种模型进行了对比,如表1 所示,其中提到的频率特征经验公式在3.1 节做了详细说明。

表1 两种统一结构对比Table 1 Comparison of two unified structures

需要说明的是,许多文献在对电力系统进行分析时均采用了类似式（4）的设备模型结构［12-14］,如文献［12］提出的经典系统频率响应模型及文献［14］中提出的对新能源高渗透电力系统采用的简化聚合频率模型,其中设备模型均与本文中统一结构模型等价。这也进一步说明了所取统一结构的合理性。

1.3 统一结构模型参数求解

求解各发电设备统一结构的参数可以看作求解一个参数优化问题,如下所示［16］:式中:ΔPi(t)为第i台发电设备实际发出的功率,ΔPi(s)为其拉氏变换后的形式；ΔP′i(t)为第i台发电设备等效为统一结构后发出的等效功率,ΔP′i(s)为其拉氏变换后的形式；Gui（s）为第i台发电设备近似的统一结构模型；t0和t1分别为优化轨迹的初始时刻与终端时刻。

为求解式（6）所示优化问题,需要知道系统共模频率响应Δω,设备模型频率-功率传递函数Gi（s）以及一阶滞后环节的时间常数T0。当这些量已知时,该优化问题实际是用3 条确定的频率相关轨迹（即sΔω、Δω以及Δω/(1+sT0)）的线性组合去逼近功率轨迹ΔPi(s),相应的系数即为Jui、Dui、1/Kui。因此,可通过最小二乘法求得这些参数。但实际上Δω可能未知（由式（1）所得频率响应的阶数非常高,不利于求解）,T0也是优化的对象。这种情况下,可考虑采用如附录C 图C1 所示方法来求解该优化问题。该方法包含外循环、内循环两个循环,分别用于解决T0以及Δω未知的问题。外循环中每次将T0增大ΔT,并将改变后的T0作为已知量代入内循环。内循环中采用文献［16］中方法迭代求解Δω,同时得到此T0下最优的Jui、Dui、1/Kui等参数,具体方法见附录C。外循环中T0取值比最优值偏小或偏大都会增大内循环中迭代求解后目标函数的数值,据此可判断T0的最优值,进而得到Jui、Dui、1/Kui参数的最优值。

2 风电机组调频动态及系统频率响应

2.1 风电机组参与调频过程分析

典型的具有二次跌落的频率轨迹如图2（a）所示,这个过程中风电机组的功率响应如图2（b）所示。图中:t0为扰动发生时刻,t1为风电机组退出调频时刻,t2为风电机组转速恢复为初始转速时刻。由图2 可知,风电机组主动参与调频过程可以分为参与调频与退出调频两个阶段［15］,具体如下。

图2 发生二次跌落时的系统频率与风电功率轨迹Fig.2 System frequency and wind power trajectory when the second drop occurs

1）t0时刻系统发生功率扰动P0,系统频率发生偏移,同时风电机组根据所设置调频控制参与调频,释放的转子动能转化为增加的输出电磁功率ΔPw(t)=Pw(t)-Pw0（其中Pw(t)为t时刻电磁功率,Pw0为风电机组初始输出电磁功率）,为系统提供功率支撑；同时,由于转子转速下降,输入机械功率Pm(t)减少（Pm（t）的变化由风电机组转子运动方程与风能吸收系数决定［20］）。

2）t1时刻风电机组退出调频,此时,风电机组将从电网吸收功率以恢复转子转速。风电机组采用恒定输出电磁功率恢复转速策略,其输出的电磁功率与输入的机械功率满足Pw(t1)=Pm(t1)-ΔPd,其中ΔPd为退出调频时刻机械功率与电磁功率差值。待转子转速增加直到稳定,风电机组重新回到MPPT 模式。风电机组退出调频并吸收有功功率引起的功率差额可能会导致频率的二次跌落。

本文主要分析风电机组调频控制引起的系统频率二次跌落现象,因此在风电机组参与调频与退出调频期间,除风电机组外其他机组控制策略不变。

根据上述分析可知,t1时刻后风电机组不再对频率波动做出有功响应,故系统统一结构参数中风电机组的部分参数将变为0。设风电机组节点为l,其统一结构中对应参数为Jul、Dul、1/Kul。那么在t1时刻,系统的参数由Jus、Dus、1/Kus突变为Jus-Jul、Dus-Dul、(1/Kus)-(1/Kul)。此外,t1时刻后风电机组将额外吸收功率恢复转速,对于系统来说可视为增加了扰动,即功率扰动由P0变为P1=P0+ΔPd+(Pm(t0)-Pm(t1))。

2.2 系统频率轨迹解析

根据上述分析,结合式（5）可得频率表达式为:

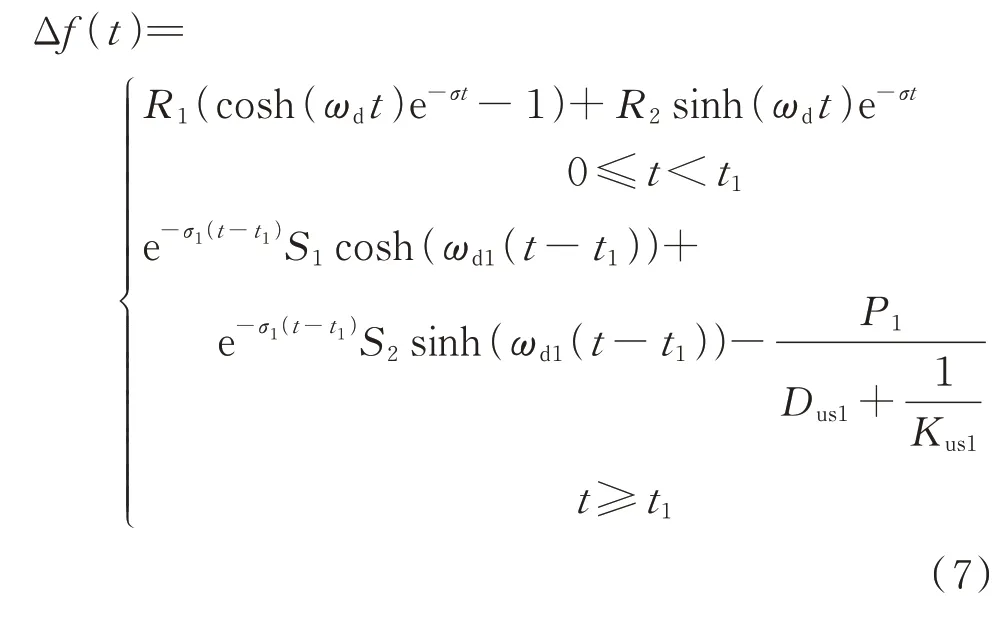
其中

其中,Jus、Dus、1/Kus为风电机组参与调频时系统统一结构参数；Jus1、Dus1、1/Kus1为风电机组退出调频后的参数；ωd、ωd1和σ、σ1分别为系统频率一次跌落与二次跌落过程中阻尼振荡频率与衰减系数。参数R1、R2与Jus、Dus、1/Kus、T0相关,参数S1、S2与Jus1、Dus1、1/Kus1及t1相关,具体表达式与推导过程见附录D。

由频率表达式同样可以看出,风电机组调频控制系数对系统频率一次跌落与二次跌落过程均有影响。

3 系统频率特征评估及风电调频参数整定

3.1 系统频率特征量化与评估

在风电机组参与调频的电力系统中,需要对频率一次、二次跌落最低点进行量化评估。此外,实际工程中,频率变化率也往往受到关注。值得一提的是,文献［16］指出频率平均变化率与初始变化率相比能更好地反映系统频率变化趋势。因此,本节将对一次、二次跌落最低点以及平均变化率3 个频率特征进行量化分析。

基于频率表达式（7）可量化风电机组并网后系统的动态频率特征。

1）一次跌落频率最大偏差

式中:tnadir1为出现一次最大频率偏差的时刻；Δfnadir1为一次最大频率偏差。

为简化Δfnadir1量化结果,提出如下估计Δfnadir1的经验公式:

该经验公式的误差分析见附录B。由附录B 可知,针对算例系统发生多种变化的情况下,该公式的误差小于10%,满足工程应用要求。

电力电子型电源（风电机组）快速调节的特性使得电力电子型电源增多,引起系统统一结构参数Jus、Dus增大。由式（10）可知,这有利于提升系统频率一次跌落最低点,有效支撑系统频率。

2）0～tp1时段内频率平均变化率Δf˙0～tp1

该经验公式的误差分析见附录B。由附录B 可知,针对算例系统发生多种变化的情况,该公式的误差小于10%,满足工程应用要求。

从以上分析可以看出,扰动初期系统支撑频率过程中,频率变化率不仅与有效惯量相关,也与有效阻尼与静态调差系数相关。而电力电子型电源的增多主要使系统统一结构参数Jus、Dus增大。这表明了电力电子型电源的增多将使得多种频率支撑的调控手段之间的控制时间尺度不再有显著的区分。

3）二次跌落频率最大偏差

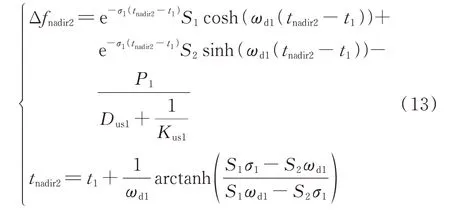
式中:tnadir2为出现二次最大频率偏差的时刻；Δfnadir2为二次最大频率偏差。

通过上述公式计算得到系统频率特征后,即可分别将其绝对值与系统允许的频率最低点最大幅值（临界值）|Δfnadir,c| 和频率平均变化率最大幅值|Δf˙0～tp1,c|做比较以评估系统频率特征:低于临界值时,说明系统频率特征满足系统调频要求。例如,当某电网要求频率最大偏差|Δfnadir,c|为0.8 Hz,则当Δfnadir1和Δfnadir2的绝对值均小于0.8 Hz 时,最低点频率特征满足要求。

3.2 风电机组调频控制参数整定

风电机组参与调频后,希望其能提升频率最低点。但如果调频参数设置不合理,风电机组在调频过程中快速释放转子动能,之后为恢复转速又从系统吸收大量能量,这可能导致频率二次跌落低于一次跌落。

为此,可将风电机组调频参数的整定视为一个优化问题。将提升一次跌落最低点作为优化目标,并将二次跌落最低点不低于一次跌落最低点作为一个约束条件。同时考虑到转子动能约束,该优化问题可描述为:

式中:HW为风电机组等效时间常数；ωr(t0)为风电机组初始转速；ωr,min为风电机组最低转速。

将上述不等式约束与目标函数构造成满足KKT（Karush-Kuhn-Tucker）条件的拉格朗日函数,通过拉格朗日乘子法与全局搜索算法嵌套即可得出风电机组主动调频过程中的最优控制下参数整定结果［21］。

上述优化问题得到的参数优化结果Jul、Dul、1/Kul为设备在统一结构下的参数,可以采用1.3 节中的优化算法实现由统一结构下的参数到实际控制参数KJ、KD的转化。具体地说,将1.3 节迭代优化算法中的优化变量改为风电机组的虚拟惯量系数KJ及下垂系数KD,再代入本节得到的参数优化结果Jul、Dul、1/Kul,即可得出风电机组的实际优化控制参数KJ、KD取值。

4 算例分析

为验证本文提出的系统频率特征评估方法的准确性及对风电机组调频参数整定方法的有效性,本章在MATLAB/Simulink 中搭建3 机9 节点系统仿真模型（参考附录E 图E1）,其中G1、G2 为同步机,WTG3 为风电机组。取容量基值SB=100 MV·A,3 台机组额定容量分别为200、100、30 MV·A。风电机组采用惯量下垂控制,如附录A 图A1 所示,同步机的模型、参数以及系统参数见附录E。

4.1 频率特征评估方法验证

首先,通过1.3 节优化算法得出各设备统一结构参数,如附录E 表E2 所示。

考虑扰动为t0=1 s 时,节点8 处发生50 MW 的功率阶跃扰动,分别取风电机组退出调频时刻t1为3、4、6 s。MATLAB 中仿真获得系统共模频率以及基于统一结构近似得到的系统频率轨迹如图3 所示。由图3 可知,在不同退出调频时刻下,基于统一结构得出的频率轨迹与系统共模频率基本吻合。

图3 风电机组参与调频时频率轨迹对比Fig.3 Comparison of frequency trajectories when wind turbines are involved in frequency regulation

设系统要求频率最低点临界值|Δfnadir,c| 为0.8 Hz,频率平均变化率临界值|Δf˙0～tp1,c|为1 Hz/s；仿真获得的频率动态特征与基于指标得到的对比及评估结果如表2 所示,其中取nt=4、t1=4 s。

表2 频率动态特征对比及评估结果Table 2 Frequency dynamic feature comparison and evaluation results

由表2 结果可知,由统一结构得出理论频率一次跌落最低点与系统仿真中一次跌落频率最低点的相对误差,二次跌落频率最低点相对误差及频率变化率相对误差均在5%以内,精度满足工程应用需求。值得一提的是,该算例中风电机组不参与调频时系统阻尼比为0.691,风电机组参与调频时系统阻尼比为0.809,均满足前文所述经验公式适用范围。

表2 所示结果表明,所建立的统一结构模型与系统有效参数计算方法能够准确分析较长一段时间内系统共模频率特性,并有效量化评估风电机组并网后系统频率动态特征。

为更好验证3.1 节所提频率一次跌落最低点及频率平均变化率经验公式适用范围,对比风电机组不同容量占比下经验公式误差结果,见附录B。由附录B 结果可知,所提经验公式在多种风电机组占比情况下误差皆满足工程应用需求,适用范围较广。

4.2 风电机组调频控制参数整定方法验证

风电机组参与调频的能量与风电机组转子动能的变化量有关。当风电机组容量增多时,可释放的动能也将增大。因此,风电机组的容量占比将对系统频率特性带来影响,最优的风电调频参数也会有所不同。

本文主要研究风电机组调频控制参数对频率一、二次跌落最低点的影响,在优化中给定了退出调频时间t1［15,22］。风电机组初始转速为1.1 p.u.,取最低转速限制ωr,min为0.7 p.u.,t1=4 s。考虑不同的风电机组容量占比,采用第3 章中方法可得到风电机组最优的惯量下垂控制参数,如表3 所示。

表3 风电机组最优控制参数整定结果Table 3 Setting results of optimal control parameters for wind turbines

由表3 结果可以看出,为满足系统调频需求,当风电机组容量占比较小（例如1.1%）时,可以释放全部的动能；而在风电机组容量占比较多的情况下,风电机组没有释放全部动能。这是因为当风电机组可释放动能较小时,其在频率一次跌落过程中的出力将被限制,使其退出调频时引起的系统等效参数的变化及新增的功率扰动都较小,因此可以释放全部的动能参与调频而不至于引起频率二次跌落比一次跌落严重的情况。而随着风电机组容量占比的增多,对参数整定的约束将由可释放动能转变为到二次跌落最低点。在风电机组容量占比较多的情况下,释放大量动能参与调频,则其退出调频时带来的系统的等效参数的变化及新增的功率扰动都较大,会引起频率二次跌落比一次跌落严重的情况。因此,在风电机组容量占比较大的情况下,参数优化后风电机组在调频过程中并不会完全释放其可用的转子能量,使得频率二次跌落最低点不低于一次跌落,这也会使得优化结果中频率二次跌落最低点趋于一次跌落最低点,正如表3 结果所示。

需要说明的是,相比于双馈风电机组,直驱风电机组最低转速限制可能更低,可用转子能量更多［7］。故由上述分析可知,当风电机组容量占比较小（优化后风电机组释放全部可用动能）时,直驱风电机组优化后的参数将大于双馈风电机组。否则,两种风电机组优化结果相近。

为验证所提调频参数整定方法的有效性,以风电机组容量占比为5%为例,对比以下几种调频参数整定方法得到的系统频率响应:1）本文所提方法；2）充分利用转子动能,并以虚拟惯量控制为主；3）充分利用转子动能,并以下垂控制为主；4）与本文所提方法消耗相同转子动能,并以虚拟惯量控制为主；5）风电机组不参与调频。

在前文所述系统及扰动下,考虑转子动能约束,以下垂控制为主时,风电机组参数Du3的最大取值约为230；以虚拟惯量控制为主时,风电机组参数Ju3的最大取值约为400；与优化结果消耗相同转子动能下虚拟惯量控制为主参数Ju3的取值为22.9。

对比上述整定参数进行仿真得到系统频率变化及风电机组转子转速变化如图4 所示。由图4 可知,在前述5 种风电机组调频控制参数整定方法中,本文所提方法可最优地提升系统频率一、二次跌落最低点。因此,利用优化问题完成风电机组不同容量占比下控制参数的整定,可以实现包括二次跌落过程的频率有效支撑。

图4 风电机组参数不同整定方式下频率及转子转速对比Fig.4 Comparison of frequency and rotor speed with different setting modes of wind turbine parameters

5 结语

在考虑风电引起频率二次跌落的情况下,本文对系统的频率特征进行量化评估,并给出了风电调频参数的优化整定方法。研究结果表明:1）基于提出的装备统一结构简化模型,可建立指标准确量化评估频率平均变化率以及一次、二次跌落最低点等频率特征；2）相比于只考虑一次跌落的风电调频参数整定方法,本文所提方法能充分考虑风电调频对二次跌落的影响,同时提升两次频率最低点,以更好地支撑系统频率。此外,考虑到新能源电力系统运行变化范围大这一特点,如何具体结合实时工况对风电参数进行整定值得进一步研究。

本文研究得到云南电网有限责任公司科技项目“高比例新能源异步电网频率强度在线评估与预警技术研究及应用”的资助，特此感谢！

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。