计及配电网线路阻抗影响的自适应接地故障消弧控制策略

涂春鸣，侯玉超，郭 祺，姜 飞，黄泽钧，姚 鹏

（1. 国家电能变换与控制工程技术研究中心（湖南大学）,湖南省 长沙市 410082；2. 长沙理工大学电气与信息工程学院,湖南省 长沙市 410082；3. 珠海万力达电气自动化有限公司,广东省 珠海市 519000）

0 引言

配电网结构复杂多变、随机性故障频发,其中约70%以上的故障为瞬时性接地故障［1］。为提高系统供电可靠性,中压配电网一般采用小电流接地方式,包括中性点不接地、中性点经消弧线圈接地等形式［2-3］。但随着配电网规模不断扩大以及电缆线路的大量使用,单相接地故障电流剧增,故障点电弧难以自行熄灭。

接地故障电弧熄灭的主要影响因素包括接地故障电流和间歇性弧光过电压［4-5］。配电网接地故障消弧方法按补偿装置可分为有源消弧法和无源消弧法［6］。消弧线圈和消弧柜［7-9］作为无源消弧装置广泛应用于配电网,但存在消弧线圈无法实现故障电流全补偿、消弧柜接地投运时冲击电流大等问题。文献［10-12］提出连续可调阻抗接地消弧装置,通过调节消弧线圈或磁控电抗器阻抗,实现接地故障容性电流全补偿,但其无法补偿有功及谐波分量。文献［13-15］提出有源电流消弧方法以实现接地故障电流全补偿。文献［13］提出一种主从式二次侧调感的零残流消弧线圈,主消弧线圈补偿大部分容性电流,从消弧线圈通过有源逆变器补偿残余容性电流、有功电流和谐波电流。文献［14］研制了三相五柱式消弧线圈,其采用可控硅调节二次电感电流,实现配电网对地电容电流的自动跟踪补偿。文献［15］提出基于级联H 桥变流器的分相电流消弧方法,其采用母线电压计算消弧电流而无须故障选相。但现有的有源电流消弧方法都需通过测量母线电压或相电压以及线路对地参数计算出所需的补偿电流,若对地参数测量不准确,会导致接地故障残流较大。文献［16-19］提出了基于零序电压柔性控制的配电网接地故障消弧与保护新原理,通过控制零序电压,可抑制间歇性故障电流或消除三相不平衡,且该方法采用双闭环控制可无须测量线路对地参数。然而,在低阻接地时,受线路阻抗和负载电流的影响,电压消弧方法可能会故导致障点残流增大,电弧难以熄灭。

为解决现有电流消弧法与电压消弧法的不足,文献［20］提出一种改进有源电压消弧算法,可将低阻接地故障电流限制在安全范围内,但安全范围会受线路参数的影响而变化。文献［21］提出计及线路参数影响的电压消弧算法,其可较为精确地控制故障点电压为零而实现消弧,但该算法仍需计算线路对地参数。文献［22-23］提出可适应线路参数变化的综合柔性消弧方法,分别以接地电阻［22］和零序电压［23］作为控制切换条件。高阻接地时,采用电压消弧法；低阻接地时,采用电流消弧法。综合柔性消弧法虽在一定程度上规避了电压、电流消弧的不足,但存在切换控制复杂、切换暂态冲击大等问题。

基于以上问题,本文提出一种自适应有源消弧方法。首先,分析了现有电压消弧方法受线路阻抗和接地电阻大小的影响机理。其次,通过对比配电网接地故障电流完全消弧与未完全消弧时线路特征参量的差异,提出将故障相负荷电流与线路电流差量转换为故障点残压补偿量,以抵消线路压降对电压消弧的影响。该方法可自适应线路参数的变化,且可将故障点电压精确抑制为0。通过分析控制系统的稳定性,证明控制策略对线路参数变化具有较强的适应性。最后,通过MATLAB/Simulink 仿真以及RT-LAB 硬件在环实验,验证了所提消弧控制策略的可靠性与可行性。

1 柔性消弧的基本原理

1.1 含消弧变流器的配电网结构

现有配电网有源消弧变流器（arc suppression converter,ASC）包括中性点注入式［19］和三相母线直挂式［15］。三相直挂式结构具有功能多样、设备利用率高等优势,在电网正常时,ASC 注入容性无功补偿电流；在电网接地故障时,ASC 注入感性消弧电流。ASC 主要以全桥和级联结构为主,含三相直挂式ASC 的配电网结构如图1 所示。ASC 采用星形连接且中性点接地,可使三相桥臂独立运行。

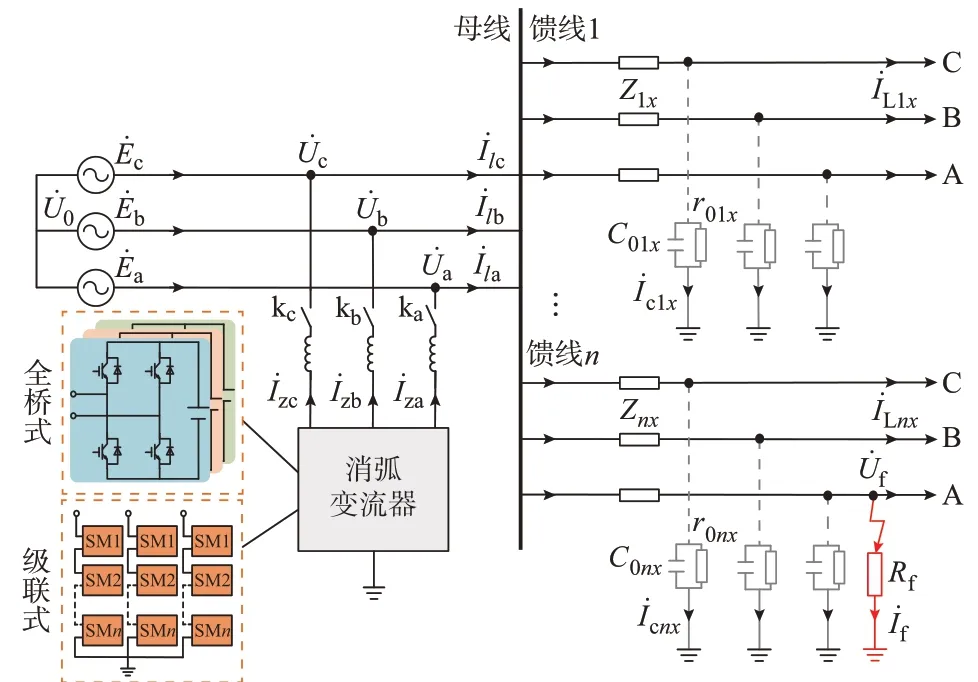
图1 含ASC 的配电网结构Fig.1 Structure of distribution network with ASC

图中:E˙a、E˙b、E˙c为三相电源电压,U˙a、U˙b、U˙c为母线三相相电压,U˙0为中性点电压,U˙f为故障点电压；I˙zx（x=a,b,c）为变流器三相注入电流,I˙lx为ASC并网点出口端三相线路电流,I˙cnx为第n条线路三相线路对地电流,I˙Lnx为第n条线路三相负载电流,I˙f为接地故障电流；Znx为第n条线路三相线路阻抗,C0nx和r0nx分别为第n条线路三相线路对地电容和电阻,Rf为接地电阻；ka、kb、kc为变流器三相高压开关。

为简化分析,将ASC 等效为受控电流源,并假设A 相发生单相接地故障。由于故障电流只在对地回路中流通,负载电流基本不受接地故障的影响,等效电路如图2 所示。图中:Y0m为非故障馈线对地零序总导纳；Y0n为故障馈线对地零序总导纳；Z为故障馈线母线至故障点的线路阻抗；U˙*f为故障点的故障前电压。

图2 含ASC 的配电网等效电路图Fig.2 Equivalent circuit diagram of distribution network with ASC

1.2 有源电压消弧的基本原理

有源电压消弧原理是通过注入消弧电流控制故障点电压为0。由于配电网接地故障点难以确定,电压消弧法一般控制故障相母线处电压为0,则故障相母线电压满足式（1）。

受配电网线路阻抗影响,线路阻抗压降ΔU˙Z约为:

由式（10）可知,有源电压消弧后的故障点残流受故障相负载电流、接地电阻和母线至故障点阻抗大小的影响。以配电网负载电流为定量（实际取值以后文仿真为例）,分别给出故障点残压幅值与接地电阻和故障距离的关系、故障点残流幅值与接地电阻和故障距离的关系,如图3 所示。

图3 接地故障点残压、残流关系图Fig.3 Relationship between residual voltage and residual current at grounding fault point

从图3 中看出,在接地电阻较小、故障距离较远时,配电网故障点电压无法精确控制为0,故障点残流较大；在接地电阻较大、故障距离较近时,故障点电压虽然不为0,但因接地电阻阻值较大使得故障点残流较小。接地电阻具有随机性且随接地时间往往存在演变过程,故低阻故障残流大将限制电压消弧方法的应用,而减小电压消弧时故障残流的本质是精确控制故障点电压接近于0。

2 自适应有源消弧方法

2.1 自适应有源消弧的基本原理

配电网发生接地故障以后,非故障相对地电容电流经故障相接地点流经网侧而形成回路,配电网零序电压及零序电流发生变化。此时,ASC 可采用单相注入、两相注入和三相注入方式［15］补偿接地故障电流,本文将以单相注入消弧电流方式为例,分析配电网线路特征参量。

根据式（10）,传统电压消弧方法受线路阻抗和负载电流影响,ASC 注入消弧电流后,故障点会存在故障残流。其等效控制配电网母线电压为0,故障电流流动路径如图4（a）所示。此时,故障相电压较低导致故障相对地电容电流较小,则故障相线路电流为:

从图4 可以看出,当故障点电流完全消弧与未完全消弧时,故障相线路电流存在明显的特征差异。

图4 故障电流流动图Fig.4 Diagram of fault current flow

故障后,故障点电压可表示为:

观察式（15）可以发现,若能够消除I˙la与I˙La之间的偏差（即I˙la=I˙La）,则可以使故障点残压为0,实现故障点完全消弧。基于这种思想,本文通过在电压参考值处增加残压补偿环路来消除线路阻抗压降对消弧带来的不利影响。其等效原理如图4（b）所示,利用残压补偿量抵消线路压降。

在控制系统中,I˙la与I˙La的差量可利用比例-积分（PI）或比例-谐振（PR）控制器实现稳态追踪。为简化控制器设计,本文以PI 控制器为例进行分析。将线路电流控制差量经过PI 控制器转化为故障残压量,如式（16）所示。

由式（17）知,要求解中性点电压参考值,需通过互感器检测故障相电源电压的负值-E˙a、线路电流I˙la以及求解出故障相负荷总电流I˙La。

由于线路阻抗远小于对地参数阻抗,配电网对地电容电流的计算可近似忽略线路阻抗影响［15］。故配电网故障前,线路电流满足式（18）。

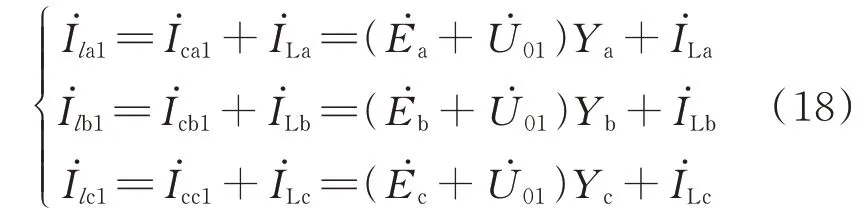
式中:U˙01为故障前中性点电压；I˙la1、I˙lb1、I˙lc1为故障前三相线路电流；I˙ca1、I˙cb1、I˙cc1为故障前三相对地电容电流；Ya、Yb、Yc为三相线路对地导纳。

配电网接地故障大多为瞬时性和间接性故障［16］,且通过相关仿真与实验发现,柔性消弧往往可以在1 个工频周期内将故障电流抑制为0［15-16,18］,故在消弧期间可忽略负荷电流的波动。配电网故障后,线路电流满足式（19）。

当B、C 相发生接地故障时,同理可以求出对应故障相的负荷总电流,这里不再赘述。

由式（21）、式（23）可得,只需通过检测故障前后各相线路电流和中性点电压即可求出故障相负荷总电流。再将式（23）代入式（17）,即可求出中性点电压参考值。从式（23）和式（17）的参考值计算结果看出,自适应消弧控制中未用到线路对地参数,因此,该控制方法不涉及对地参数测量。

2.2 控制策略分析

2.2.1 消弧装置整体控制策略

仿真中ASC 采用级联结构,主要实现2 种功能:1）电网正常时,ASC 处于无功补偿模式；2）接地故障时,ASC 处于柔性消弧模式。系统整体控制框图如图5 所示,包括子模块均压环控制、无功电流计算、故障残压补偿控制、消弧外环电压控制、消弧内

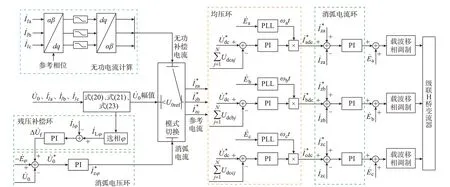
图5 整体控制框图Fig.5 Overall control block diagram

1）无功补偿模式。当检测中性点电压幅值小于阈值U0ref时,ASC 处于无功补偿模式。均压环节采用PI 控制,主要用于维持子模块直流电容电压稳定,防止因H 桥自身损耗而引起直流电压跌落。无功电流计算模块采用瞬时无功理论,得到各相无功补偿电流参考值。内环电流采用PI 控制,使ASC输出电流跟踪无功电流参考值。

2）柔性消弧模式。当检测中性点电压幅值大于U0ref时,ASC 切换至柔性消弧模式。首先,检测各相线路电流；根据式（20）、式（21）、式（23）选相并计算故障相负载电流I˙Lφ,I˙Lφ与故障相线路电流I˙lφ作差,经PI 控制得到消弧残压补偿量ΔU˙f,将ΔU˙f叠加到消弧电压外环并经PI 控制器得到消弧电流参考值I˙*z。得到I˙*z后,理论上可以控制ASC 任意一相进行消弧,但因故障相并网点电压接近于0,导致实际运行中很难维持故障相ASC 正常运行。因此,本文在仿真中选择非故障相中的一相注入消弧电流。

2.2.2 控制策略稳定性分析

为避免线路对地参数测量误差对消弧效果的影响,较多文献采用双闭环控制方法［18-19］,并对其控制参数设计和稳定性进行了详细分析。本文在计及线路阻抗影响下,通过增加残压补偿环节对双外环参考值进行修正,其等效控制框图如图6 所示。为简化控制器参数设计,本文采用PI 控制器对控制方法的稳定性进行分析。

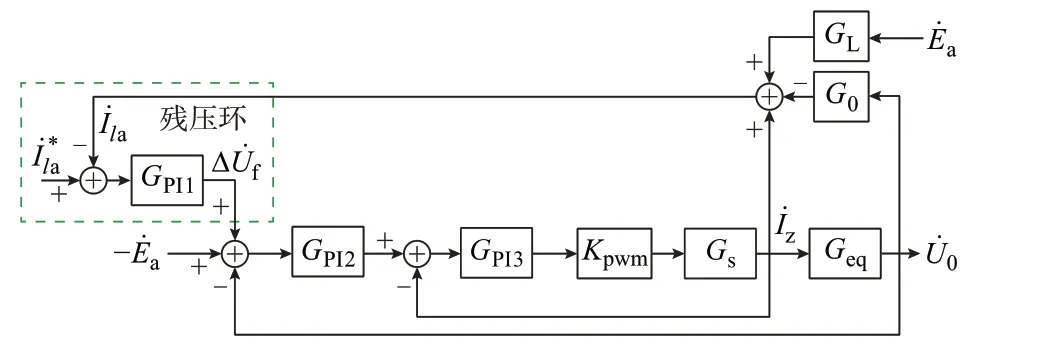
图6 消弧等效控制框图Fig.6 Equivalent control block diagram of arc suppression

图6 中:GPI1、GPI2、GPI3为PI 控制器传递函数；Kpwm为逆变器比例系数；Gs为逆变器输出电压与注入电流间的传递函数；Geq为注入电流与零序电压间的传递函数；G0为零序电压与对地电容电流间的传递函数；GL为系统电压与负荷电流间的传递函数。控制系统的传递函数为:

式中:Gs=1/(sL+Geq),Geq=ZafZbZc/(ZafZb+ZafZc+ZbZc),G0=ZaZbZc/ZaZb+ZaZc+ZbZc,Zaf=r0aRf/(r0a+Rf+sC0ar0aRf),Zx=r0x/(1 +sC0xr0x)+rZ+sLZ；r0x、C0x分别为x相对地电阻和电容；L为滤波电感。

传递函数中的系统参数见附录A 表A1,控制器参数可根据根轨迹图［19］或主导极点法［24］设置,但通常需大量试凑。本文结合根轨迹图和试凑法得到各PI 控制器仿真参数为Kp3=0.017 5,Ki3=50；Kp2=0.2,Ki2=300；Kp1=5,Ki1=40 000。文献［19］已验证双闭环控制系统的稳定性,故本文主要验证增加残压环后控制系统的稳定性。附录A 图A1、图A2分别给出不同接地电阻和不同故障距离时系统的波特图。从图中看出,接地电阻和故障距离变化时,系统的相角裕度基本维持在60°左右,系统稳定性好且对线路参数变化具有较强的适应性。

3 自适应有源消弧基本流程及方案对比

3.1 自适应有源消弧的基本流程

由式（20）可知,当配电网未发生接地故障时,线路电流变化量为0；当配电网发生接地故障时,故障相线路电流变化量远大于非故障相,且根据KCL定律,故障相电流变化量与非故障相电流变化量相位相反。因此,式（20）可作为配电网故障感知、故障选相的判断条件。

自适应有源消弧流程如附录A 图A3 所示。首先根据零序电压和线路电流,判断是否发生故障。配电网未发生故障时,ASC 处于无功补偿模式。配电网发生接地故障后,结合式（20）、式（21）、式（23）进行故障选相并计算故障相负载电流I˙Lφ,经非故障相ASC 桥臂注入消弧参考电流。经短暂延时后,减小注入电流以判断故障是否消除。根据电路齐性定理:在线性电路中,当激励电流减小时,响应的零序电压也将同比例减小,判定故障消除,否则故障未消除。若故障消除,配电网恢复正常运行；若故障未消除,判定为永久性故障,选出故障线路并隔离。

3.2 消弧方案对比

结合上述分析,将本文所提控制策略与文献［9,15,19,21-22］所提消弧方法在不同接地情况下进行对比,结果如表1 所示。故障相接地法投运时冲击电流较大,有可能威胁人身、设备安全；有源电流消弧方法不仅需要测量对地参数,且存在高阻接地故障消弧时间长的问题；有源电压消弧方法虽不用测量对地参数,但在低阻接地时,可能受线路阻抗影响而导致故障残流较大；改进电压消弧方法虽然适用于低阻接地,但需要测量对地参数；综合消弧方法虽可规避有源电压和电流消弧方法的不足,但该方法存在严重的暂态切换问题。然而,本文所提控制方法相对于现有消弧方法都具有明显优势。

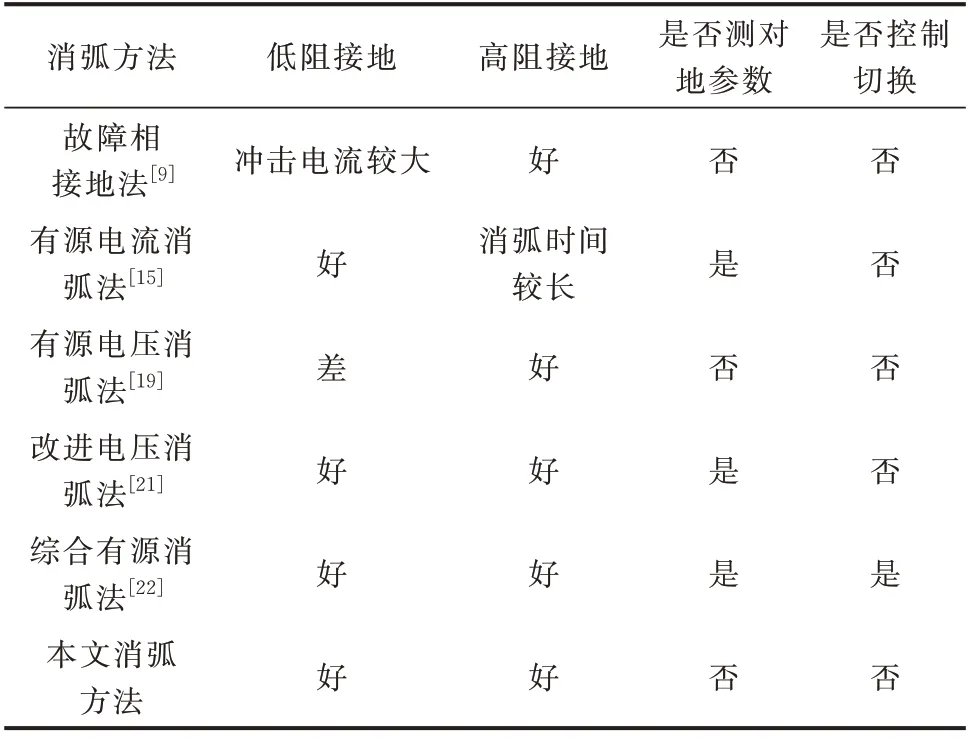
表1 消弧方法对比Table 1 Comparison of arc suppression methods

4 仿真与实验验证

4.1 仿真分析

为验证本文所提有源电压消弧方法的有效性,在MATLAB/Simulink 仿真环境中搭建了10 kV 配电网仿真模型,仿真参数如附录A 表A1 所示。

4.1.1 负载电流计算验证

为验证负荷电流的计算精度,结合附录A 表A1分别对不同接地电阻情况进行计算验证,结果见表A2。负荷电阻RL=77 Ω、负荷电感LL=0.25 H 时,实际故障相负荷电流I˙*La为68.94∠-43.67°A；当接地电阻分别为1 000 Ω、100 Ω、5 Ω 时,负荷电流计算值 为 68.99∠-43.66° A、68.96∠-43.68° A、68.97∠-43.69° A。RL=50 Ω、LL=0.15 H 时,I˙*La为105.19∠-39.95° A；当接地电阻分别为1 000 Ω、100 Ω、5 Ω时,负荷电流计算值为105.25∠-39.96°A、105.21∠-39.98° A、105.24∠-39.97° A。从附录A 表A2 看出,接地电阻大小对负荷电流计算几乎无影响,且负荷电流计算的精确度较高。

4.1.2 自适应有源消弧方法验证

为验证本文所提控制策略的优越性和可靠性,结合附录A 表A1 仿真参数,进行传统有源电压消弧方法（即不加残压补偿环）和自适应有源电压消弧方法仿真对比,如附录A 图A4 至图A6 所示。假设配电网A 相在0.1 s 发生接地故障,为对比消弧效果,ASC 的B 相桥臂在0.3 s 注入消弧电流。在0.3～0.4 s,ASC 采用传统电压消弧控制策略；在0.4～0.5 s,ASC 采用自适应消弧控制策略。

附录A 图A4 为Rf=1 000 Ω 时仿真波形,在0.1～0.2 s,ASC 处于无功补偿模式,系统电压E˙a与系统电流I˙sa处于同相位；在0.2 s,配电网发生接地故障,中相点电压U˙0为1 180 V,故障点电流I˙f为7.45 A；在0.3～0.4 s,ASC 采用传统电压消弧控制方法,故障点残压为760 V,故障点残流为0.76 A；在0.4～0.5 s 采用自适应消弧控制方法,故障点残压为60 V,故障点残流为0.06 A。

附录A 图A5 为Rf=100 Ω 时的仿真波形,在0.1～0.2 s,ASC 处于无功补偿模式,系统电压E˙a与系统电流I˙sa处于同相位；在0.2 s,配电网发生接地故障,中相点电压U˙0为6 220 V,故障点电流I˙f为40.7 A；在0.3～0.4 s,ASC 采用传统电压消弧控制方法,故障点残压为680 V,故障点残流为6.8 A；在0.4～0.5 s 采用自适应消弧控制方法,故障点残压为15 V,故障点残流为0.15 A。

附录A 图A6 为Rf=5 Ω 时的仿真波形,在0.1～0.2 s,ASC 处于无功补偿模式,系统电压E˙a与系统电流I˙sa处于同相位；在0.2 s,配电网发生接地故障,中性点电压U˙0为7 604 V,故障点电流I˙f为49.8 A；在0.3～0.4 s,ASC 采用传统电压消弧控制方法,故障点残压为238 V,故障点残流为47.6 A；在0.4～0.5 s 采用自适应消弧控制方法,故障点残压为2.2 V,故障点残流为0.45 A。

为进一步验证配电网三相对地参数不平衡工况下自适应消弧控制方法的有效性,分别取A、B、C 三相对地参数为7、9、8 μF,其他仿真参数与附录A 表A1保持一致,仿真波形如附录A 图A7 所示。从图A7中看出,在配电网正常运行时,受线路对地参数不平衡影响,配电网中性点电压为560 V。当采用传统电压消弧方法时,Rf=1 000 Ω 接地故障情况下,故障电流由8.0 A 减小至0.88 A；Rf=100 Ω 接地故障情况下,故障电流由45.5A 减小至7.0 A；Rf=5 Ω 接地故障情况下,故障电流由58.9 A 减小至48.8 A。因此,传统电压消弧依然存在高阻接地时消弧效果较好、低阻接地时消弧效果较差的问题。当采用自适应消弧方法时,Rf=1 000 Ω 接地故障情况下,故障电流减小至0.06 A；Rf=100 Ω 接地故障情况下,故障电流减小至0.15 A；Rf=5 Ω 接地故障情况下,故障电流减小至0.5 A。因此,在三相对地参数不平衡工况下,自适应消弧对低阻和高阻接地故障依然具有良好的消弧效果。

4.2 实验分析

基于以上仿真模型,搭建了RT-LAB 硬件在环实验平台。主电路仿真模型位于主控制器中,外部控制选择DSP28335 控制器,实验参数与附录A表A1 保持一致。

附录A 图A8至图A10分别为Rf=1 000、100、5 Ω时的实验波形。从实验波形看出,在电网正常运行时,电网电源电压与网侧输出电流同相位。在发生接地故障且未进行消弧时,配电网中性点电压发生偏移,且接地故障电流随接地电阻减小而增大。当采用传统电压消弧时,Rf=1 000 Ω 接地故障情况下,故障电流减小至1 A 左右；Rf=100 Ω 和Rf=5 Ω接地故障情况下,故障残流较大,消弧效果差。当采用自适应电压消弧时,任何接地故障情况下,故障电流都接近于0。因此,充分证明自适应消弧方法对接地参数变化具有良好的适应性。

5 结语

本文通过分析配电网接地故障电流完全消弧与未完全消弧时线路特征参量的差异,提出一种自适应有源消弧控制方法,得出如下结论:

1）本文所提自适应消弧控制策略,对于任何接地故障情况,都可将故障点电压抑制为0,有效防止故障点电弧重燃；

2）该控制策略无须测量线路对地参数,具有消弧效果好、控制算法易于实现等优势；

3）通过分析控制系统稳定性,证明控制方法对不同故障距离和故障电阻都具有较强的适应性和可靠性。

在本文研究的基础上将进一步解析电网谐波、负载电流波动等对所提控制方法的影响。由于实验条件限制,所提控制方法未能进行实物平台验证。下一步将搭建配电网接地故障调控测试平台,开展更加细致的实验验证。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。