滑移线连续和平稳分布的变径车轮设计
殷勇辉 陈司晨
华东理工大学机械与动力工程学院,上海,200237
0 引言
轮式结构在平坦路面上具有快速移动能力,但在松软、崎岖、复杂地形及未知环境的机动性和越障能力有限[1]。腿式结构具有良好的越障性能[2-3],但行走速度低、效率低,结构和控制系统相对比较复杂[4]。履带式结构具有地形适应能力强、越障性能良好、动载荷小、结构紧凑等优点,但整体结构笨重、能耗大[5]。具备多种运动优势的轮足、轮履等复合结构和变形结构的出现,提高了车辆的地形适应性和机动性[6-9]。
变径车轮既保留了传统车轮的移动速度优势,其灵活可调的车轮直径又提高了车轮的运动性能和对复杂地形环境的适应性,有效避免了发生陷困、打滑导致无法行驶和作业的问题。变径轮具有承载、牵引和移动功能,与工作环境的地表直接接触,在设计移动装置、评价通过性能和分析非常规路面领域,深入开展变径车轮与地面之间交互作用力学的研究具有重要的意义。
对传统车轮-土壤接触模型的分析自20世纪60年代开始[10],许多学者开展了轮地剪切接触模型改进和实验研究。IRANI等[11]建立了带刚性轮和履带板的小型轻型车辆的沙质土壤动力学模型,通过数值分析和仿真实验证明了轮周应力的周期性,改进了轮刺应力效果较明显时的土壤力学模型。SUTOH等[12]对带轮刺的车轮在松软土壤中的运动进行实验研究,分析了轮刺效应带来的运动学影响和轮刺的分布方式,从车体线性移动速度的角度研究履带轮式车体在高速运行下的周期性速度波动成因,得到了最大允许履带齿间距。NAKAMURA等[13]基于粒子图像测速法 (PIV)对轮刺效应及土壤流动滑移情况进行了实验测定,得到了土壤流动滑移的实际情况,进而定量分析了履带轮下方土壤的流动滑移,推导了土壤流线和滑移线分布模型,但未给出更具有说服力的土壤相互作用模型。丁亮[14]研究了星月探测车刚性轮-软土牵引特性,从连续剪切的角度初步推导出轮刺高度、倾角及个数的关系,但未对实际接触的滑移线分布进行分析,也没有从土壤滑移剪切的土力学角度出发进行研究[15-16]。陈新波等[17]证明其设计的变径轮在松软土壤中具有更大的牵引力、力矩和效率,并能减小动态沉陷量,但研究仅停留在传统车轮剪切滑移模型,没有对变径轮的实际土壤剪切滑移情况进行分析。曲杰等[18]对轮履复合式变形车轮进行结构和参数的设计,分析了其爬坡性能和翻越台阶性能,但并没有从实际的土壤接触角度分析变径轮的运动特征。孙中兴等[19]对柔性履带在土壤滑转流动特性进行研究,改进了传统履带-地面应力分布模型。
目前,变径轮的研究主要集中于变径或变形结构系统设计,对其越障性等运动特性仅利用简化结构模型进行分析和实验,而从实际土壤剪切模型出发分析变径轮运动特性的文献比较缺乏。车轮与土壤的剪切接触过程是影响车轮运动性能的主要因素,车轮与土壤接触过程中形成的土壤滑移线直接影响车轮的沉陷和运动特性,因此从土壤滑移线的角度对变径轮分析是必要的。
笔者设计的变径轮具有灵活可控的轮径,且车轮的整体刚度高,在松软表面运动时的车轮沉陷量更小并具有更好的通过性。基于土壤剪切流动原理,通过分析变径轮不同断面结构与沙壤土作用机理和滑移线分布规律可以发现,当存在外轮周空穴的变径轮在沙壤土环境中运动时,内轮片-土壤接触区的滑移线分布可通过合适的断面以及轮刺设计使内轮片-土壤接触区实现完全的土壤滑移线覆盖,将内轮片表面的土壤-金属轮片摩擦转化为土壤-土壤摩擦,增大土壤对变径轮提供的牵引力,提出了变径轮与土壤作用滑移线平稳性和连续性分布的设计准则,确定了断面参数和轮刺参数之间的耦合关系。
1 变径轮设计
1.1 变径轮结构
如图1所示,变径轮通过悬架结构与车体连接,车轮由内外两层刚性厚轮片、轮径扩展架、变径驱动机构、锁紧机构等组成。

(a)变径轮-土壤接触模型
变径轮的内外轮片各有6个,每个轮片对应的轮片角为60°。扩展架位于外轮片中轴线上,连接外轮片与变径轮轮心。通过滚珠和滑移轨道实现内外轮片的连接,如图1b所示。变径驱动机构带动轮径扩展架径向运动,实现内外轮片的同步扩展或收缩,并使内外层轮片始终保持贴合状态。通过控制驱动机构中的舵机转动角度可改变轮径和外轮片之间的间隙。变径结束后,锁紧机构固锁住轮径扩展架,形成一个整体转动结构。
轮径扩大过程中,厚度较大的轮片使得扩展后的车轮周向呈现凹凸状(图1a中的A点和B点)。为利用内外轮片与土壤接触部分的交错层断面效应,在A点和B点处设计有对称的小角度倾角,并在内轮片中部C点处设计倾角可调的轮刺(图1c)。
1.2 变径轮特点
目前常见的变径轮结构在轮径扩大后通常会出现轮片分离,形成轮周的镂空结构,这不仅使变径轮表面的受力不平稳、产生运动颠簸,还会增加轮体的磨损,大大缩短寿命。
结构设计方面,变径轮内外轮片的互补结构可实现轮周封闭,避免轮周的分离空缺问题。通过轨道和活动滚珠的连接机构设计,大大简化了变径结构。采用对称的小倾角结构,避免了轮片产生的前后运动不对称。
运动决策方面,变径轮在普通的平坦地形保持最小轮径状态,如传统车轮一样正常行驶。在松软土壤或复杂地形条件,如遇到障碍或发生陷困、打滑时,通过扩展轮径,形成轮片断面和轮刺,并利用断面和轮刺带来的附加剪切土壤反作用力,为车体提供更大的牵引力,可有效提高环境通过性能和越障能力。遇到坡度较大的表面时,通过调整轮径来减小车体的倾斜度、避免侧翻。
2 变径轮与土壤作用模型研究
2.1 变径轮与土壤作用滑移线分布
变径轮处于最小状态时,A、B、C处紧密贴合,变径轮和传统车轮无异,土壤剪切滑移发生在刚性轮外轮片表面和土壤之间,土壤对车轮的作用力为土壤与轮周的摩擦力,即金属与土壤的摩擦力。
根据Rankine被动土压力理论,土壤与轮周作用的滑移线模型如图2所示,其中,附加应力q的作用面为直面,h为剪切高度,Xc为土壤底角,轮周与竖直方向的夹角为ξ。土壤剪切滑移模型包括图2所示的两区域模型(图2a)和三区域模型(图2b),在保持轮刺高度和土壤参数一定的情况下,模型的选择仅取决于倾角大小。从普朗特尔剪切滑移面的几何形状关系可以确定两区域模型和三区域模型所符合的倾角方位[20]。图2a中,ADE为Rankine被动区(Ⅲ区),AEF为径向剪切区(Ⅱ区),剪切滑移线FED由对数螺旋滑移线EF和直线ED表示。图2b中,ADE为Rankine被动区(Ⅲ区),AEF为径向剪切区(Ⅱ区),AFG为Rankine主动区(Ⅰ区),剪切滑移线GFED由直线GF、ED和对数螺旋滑移线FE表示。
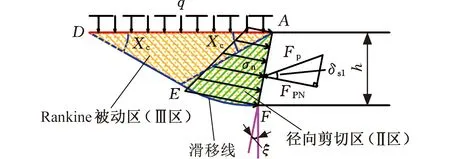
(a)两区域模型
土壤与(金属)轮片的摩擦角δsm小于土壤与土壤摩擦角δss,为增大车轮的牵引力,通常会在车轮表面进行不平整处理,如橡胶轮胎表面的纹理设计、轮周表面的轮刺设计等,轮面的凹凸设计可在轮周凹陷部分形成土壤滑移区,将金属与土壤的摩擦尽可能转换为土壤与土壤的摩擦,以增大土壤对车轮作用的牵引力。
变径轮处于扩展状态时,土壤与变径轮的相互作用比较复杂。轮周表面的滑移线分布主要为以下两种:
(1)非完全连续的滑移线分布。如图3a所示,由于在内轮片中部C点处存在一个轮刺,因此内轮片与土壤接触区域被分为AC段和CB段。A点处断面与C点处轮刺均会剪切土壤,其反作用力使得车轮的牵引力增大。图3a中,A点处断面的滑移线没有延伸到C点处轮刺位置,C处的滑移线也没有延伸到B点处断面。滑移线覆盖的部分,滑移线与内轮片间会形成固结土壤;滑移线未覆盖的部分,内轮片表面金属直接与土壤接触。内轮片与土壤在接触区AC段和CB段上既包含固结土壤与滑移线外侧流动土壤之间的摩擦,又包含金属轮周表面与滑移线外侧流动土壤的直接摩擦。
(2)完全连续的滑移线分布。如图3b所示,当A点处断面、C点处轮刺、B点处断面之间的距离不大时,A点处断面的滑移线延伸到C点处轮刺位置,C点处轮刺滑移线延伸到B点处断面,即在AC段和CB段,滑移线均完全覆盖内轮片与土壤的接触区域,滑移线与内轮片表面间会形成固结土壤,将金属轮周表面与土壤的直接摩擦转化为固结土壤与土壤之间的摩擦,此时内轮片与土壤接触区AC段和CB段上仅存在固结土壤与滑移线外侧流动土壤之间的摩擦。

(a)非完全连续 (b)完全连续
根据土壤流动滑移理论,滑移线内部的土壤可认为是固结土壤,固结土壤在运动过程中固结于内轮片表面,与车轮一起运动,形成了连续的剪切土环。定义剪切土环半径为等效轮周半径,则连续滑移线可以近似认为是等效轮周。通过对剪切作用面的间隔位置及高度的设计,可实现内轮面处的完全连续滑移线分布,使变径轮在运动过程中的稳定性和受力均匀性大大增强。
2.2 剪切滑移断面处滑移线模型分析
2.2.1剪切滑移断面处的土壤流动机理
变径轮A点处断面与土壤接触部分如图4所示。随着车轮转动,断面与断面处沿车轮转动方向后方的土壤发生挤压和剪切,断面后方处土壤对外轮片A点处断面产生较大的反作用力(牵引力)。根据土力学理论,断面使其后方土壤发生剪切滑移运动,将这种使土壤发生剪切滑移运动的断面命名为剪切滑移断面(下文简称为“断面”)。
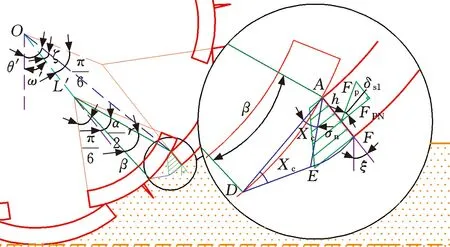
图4 剪切滑移断面处的土壤接触示意图
2.2.2剪切滑移断面的土壤作用模型

(1)
(2)
h(γ)=heγtan φ
(3)
(4)
(5)

断面倾角为φ时的土壤滑移线改进模型如图5b所示,土壤滑移线为D′E′F′。倾角为φ时的土壤滑移线模型为

(a)无倾角断面
(6)
(7)
h(γ′)=h′eγ′tan φ
(8)
(9)

2.3 主动填土断面处的滑移线模型分析
2.3.1主动填土断面处的土壤流动机理
变径轮B点处断面与土壤接触部分如图6a所示。从车轮的运动方向看,根据土力学作用原理,B点处断面类似主动土挡土墙,车轮的运动使轮壁和土壤间产生空穴,由于土壤颗粒间存在挤压且轮片对土壤存在挤压,因此黏性主动土壤发生流动进而填补空穴[20]。故此处的土壤流动是由断面运动形成的黏性主动土堆积空穴造成的,这种形成主动土堆积填补空穴现象的断面可命名为主动填土断面。
2.3.2主动填土断面处的土壤作用模型
对于主动填土断面,采用美列什科夫的对数螺旋线型滑裂面理论[22]对该断面处的土壤流动情况进行分析。选取微元土壤比较A、B两处作用力的大小,A点处断面被动土和B点处断面主动土的Rankine土力学模型如图6所示。根据轮体的转动方向,A点处断面附近的土壤为被动土,AD′为被动土滑移线;B点处断面附近的土壤为主动土,BD为主动土滑移线。

(a)主动土 (b)被动土
根据Rankine土应力理论的极限平衡原理,pb为主动土压力,pa为被动土压力,如图6所示,作用于微分土体的水平应力σb1即为主动土压力pa,作用于微分土体的水平应力σa1即为被动土压力pb,γβ为土壤容重,z为土壤微元所处的沉陷深度,φ为土壤内摩擦角,c为土壤黏聚系数。当剪切滑移断面处的土壤沉陷深度与主动填土断面处的土壤沉陷深度近似时,有
(10)
本文取γβ=2.4×104kN/m3,φ=38°,c=1.38 kPa。土壤黏度引起的土壤压力比土壤比重引起的土壤压力小得多,估算时可忽略。在相同的沉陷深度下可求得pa>14pb,因此A点处断面土壤压力pa远远大于B点处断面土壤压力pb[23],即A点处剪切滑移断面的被动土压力远大于B点处主动填土断面的主动土压力。从土壤流动机理的角度分析,在主动土的作用下,主动填土断面处较难形成固结土壤。对于黏度小的土壤,该处的空穴会在土壤内应力和负载的作用下快速填充,土壤对断面的正应力由填充土壤提供,因此作用力不大。对于黏度大的土壤,该处的空穴在土壤颗粒间的挤压作用和土壤内应力作用下逐渐填充,此过程中的作用力并不大。因此主动填土断面处的土壤对断面的作用力小,故变径轮不考虑B点断面处的土壤滑移线,直接用B点处断面来代替滑移线。
2.4 剪切轮刺土壤滑移线模型
如图1a所示,C点处轮刺对土壤的作用机理同带倾角的A点处断面一致,土壤流动作用机理都是属于剪切土壤的方式,因此对这类轮刺统称为剪切轮刺。
基于普朗特尔剪切破坏理论和传统土壤滑移线模型进行分析,与A点处相比,C点处存在两种可能的滑移模型,对应的滑移线分别为K′J′I′和K′P′N′,如图7所示,令轮刺倾角为ψ,以区别于断面倾角φ。变径轮在最大轮径状态下时的内轮片半径r远大于C点处的可调轮刺的高度h,因此可估算∠K′C′M′≈φ。

(a)两区域模型

(11)
图7b中,剪切区为普朗特尔剪切Ⅰ区和剪切Ⅱ区(剪切Ⅲ区此时在轮体内部,故仅有剪切Ⅰ区和剪切Ⅱ区),有
(12)
(13)
3 结果与讨论
3.1 连续滑移条件下剪切滑移断面倾角的影响
定义变径比η=(r+L)/r,本文中,最小轮径r=100 mm,轮径最大扩展长度Lmax=75 mm,则变径比η=1.75,无倾角状态时,土壤滑移区对应的内轮片角βmax=41.194°,内轮片与土壤接触的最大土壤接触角αmax=52.358°,土壤内摩擦角φ=38°,如表1所示。断面倾角为负会减小水平推力,因此倾角取正值进行分析。表1中,倾角φ为A点处断面和B点处断面的倾斜角度,完全覆盖轮扩角α′max为一定倾角状态下,可实现滑移线完全覆盖的最大轮扩角大小,最大轮扩对应的轮片角βmax为Lmax=75 mm时滑移线可覆盖的最大轮片角大小,最大覆盖变径比ηmax指轮扩角为完全覆盖轮扩角时的变径比,用于表征滑移线完全覆盖内轮片-土壤接触区时的最大轮径扩展程度。
结合式(6)~式(9)获得断面不同倾角φ下,轮扩角α与土壤滑移线对应的内轮片角β的关系,见图8,阴影区表示滑移线可完全覆盖内轮片-土壤接触区的范围。满足完全滑移条件的具体数据如表1所示。
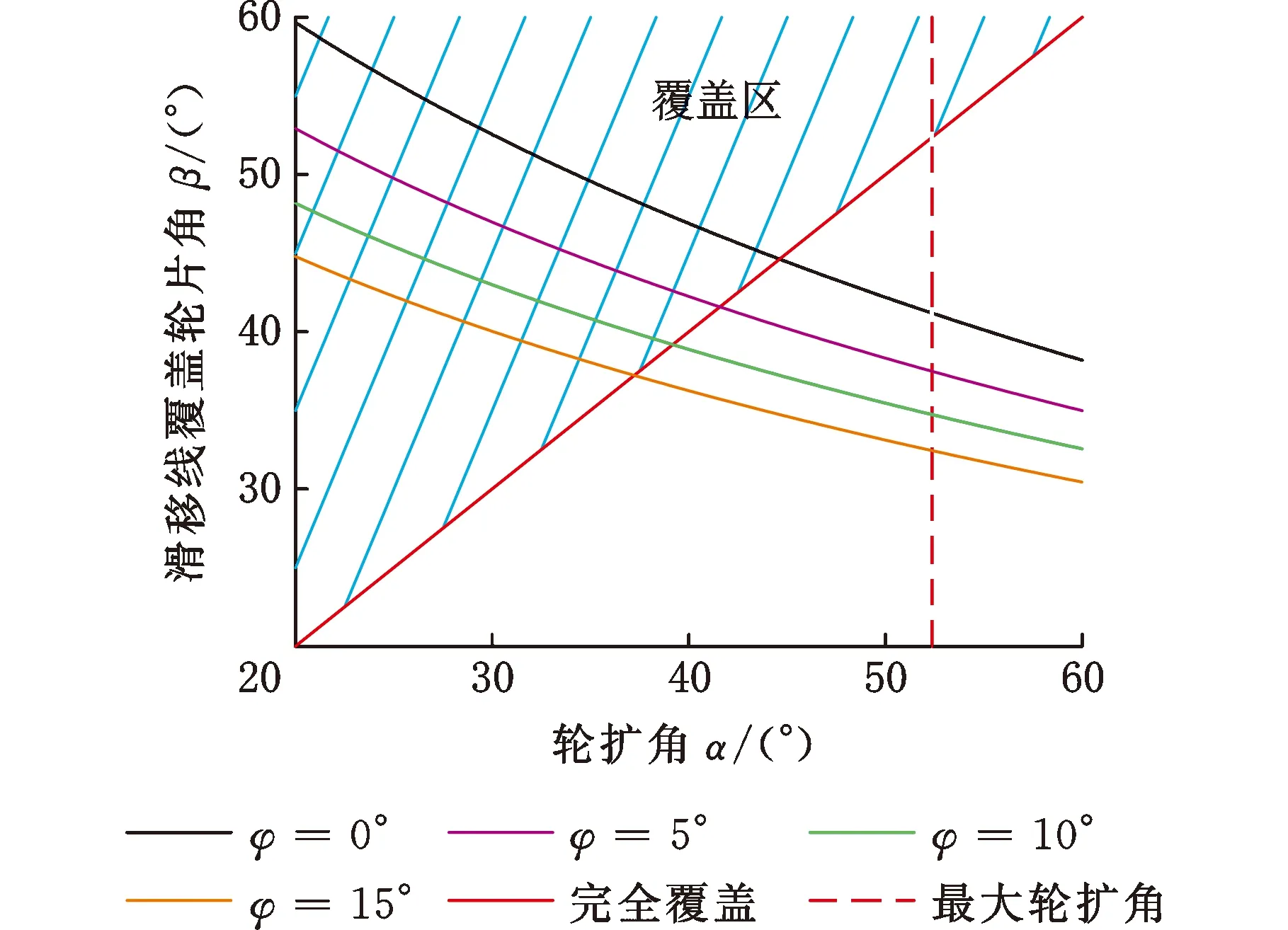
图8 断面处轮扩角α与内轮片角β的关系

表1 断面处轮扩角α与最大覆盖变径比ηmax
从滑移线连续的角度可知:①正倾角φ会造成土壤滑移线对应的内轮片角度βmax减小;②倾角φ越大,完全滑移线覆盖轮扩角α′max越小;③由表1可以发现,当仅设计有A点处断面和B点处断面时,无倾角状态对应的β0=41.194°<αmax,对应最大变径比ηmax=1.645,此时满足完全滑移线覆盖的最大轮扩角α′max=44.620°,无法实现本文设定的变径比η=1.75;④若在中部C点处设计可调轮刺,则可在内轮片与土壤接触区形成两段滑移线,如图3b所示,那么存在可调轮刺的断面滑移线所需覆盖的内轮片范围相较于仅存在断面时减半,从而大幅增大变径比。
3.2 连续滑移条件下可调剪切轮刺倾角的影响
可调轮刺处土壤剪切流动滑移模型如图7所示,基于普朗特尔剪切破坏理论和传统土壤滑移线模型,C点处轮刺的滑移线存在两种模型,令轮刺倾角为ψ,以区别于断面倾角φ。从图7滑移线分布可以看出,ψ≤β/2-Xc时,剪切区为普朗特尔剪切Ⅰ区和Ⅱ区;ψ>β/2-Xc时,剪切区为剪切Ⅱ区和Ⅲ区。轮刺两区域滑移线模型与三区域滑移线模型的分界倾角ψ0=7.0426°。
由图9可以看出,可调轮刺倾角ψ≤20°时,该轮刺处的土壤剪切滑移线覆盖角最小为52.010°,远大于αmax/2,保证了该段土壤滑移线可以完全覆盖轮刺与下一断面之间内轮片与土壤接触区。

图9 轮刺倾角ψ与土壤流动滑移角对应的内轮片角 β之间的关系
由图9可以得到,轮刺倾角ψ=0°时,完全覆盖轮扩角α″max=76.368°,随着轮刺倾角的增大,完全覆盖轮扩角α″max逐渐减小;轮刺倾角ψ=20°时,完全覆盖轮扩角α″max=52.010°,均为大于C点处轮刺的滑移线所需覆盖的最大轮扩角αmax/2=26.179°。可以发现:①倾角相等时,可调轮刺处的滑移线覆盖范围比剪切滑移断面处的大;②与剪切断面倾角类似,轮刺倾角θ越大,完全滑移线覆盖轮扩角α越小;③轮刺倾角不大于20°时,可以实现轮刺至后断面的内轮片-土壤接触区的完全覆盖。考虑到最小轮径状态下轮周为完整圆形轮廓,且C点处可调轮刺具有角度灵活控制的特点,因此对于A点处断面和C点处轮刺的倾角设计,采用优先考虑A点处断面的倾角设计,并使C点处轮刺的倾角与A点处断面的倾角保持相同大小且高度相同的策略。
3.3 连续滑移条件下的变径轮滑移线变化
为分析剪切断面连续滑移曲线形成的等效轮周半径,选择一组内轮片和外轮片接触区域进行研究,如图10所示。定义变径轮内轮片中部C为零度位置点,研究区域对应的轮心角度θ′为-12.81°~47.19°。轮周表面固结土壤所形成的等效半径可用滑移半径rs即滑移线与轮心O的距离表示,如图11所示。

图10 变径轮研究区域示意图

图11 断面对滑移半径分布的影响
由图11所示的4种断面倾角状态下的滑移半径结果可以看出:①固结土壤填补了内外轮片断面附近的半径骤变空穴区,使得作为实际运动轮廓的滑移半径相比于实际轮周波动更小(固结土壤可认为是运动轮周的一部分);②滑移半径随剪切断面倾角的增大而减小,但依然可以实现对内外轮片断面附近的半径骤变空穴区的填充。
基于前述的土壤剪切流动滑移模型,取轮刺高度和外轮片厚度相同,可获得滑移半径示意图(图12a)。C点处的可调轮刺产生的滑移线(Ⅱ区)在轮刺至B断面区域很好地补充了轮片的空缺,如图12b所示,作为实际运动轮廓的滑移半径分布相比于实际轮周波动更小,因此“断面+轮刺”的设计方案使得运动轮廓趋于平稳,从而减小运动波动并实现了内轮片-土壤接触区的连续滑移线分布。
3.4 基于滑移线平稳覆盖的设计方法
由图5、图7可以看出,对于由对数螺旋滑线和直线组成的土壤滑移线[17],土壤滑移线在DE(图5a)、D′E′(图5b)和I′J′(图7a)这三个直线段,滑移半径快速减小,滑移轮廓快速贴近内轮片。由图12a可以发现,直线滑移线部分不仅会造成自身固结土壤厚度的快速减小,还会在轮刺位置形成较明显的半径差K′M′。根据土壤流动滑移理论,滑移线内部的土壤固结于内轮片表面,滑移线可以近似认为是等效轮周,因此若A点处断面和C点处轮刺的滑移线仅包含对数螺旋线部分,即滑移线末端如图12a的点Q′和点M′处依然处于二区域模型的Ⅱ区内(图2a)或三区域模型的Ⅱ区内(图2b),此时内轮片处的固结土壤可较平稳覆盖内轮片-土壤接触区。

(a)变径轮土壤剪切流动滑移模型
无倾角状态下,形成于内轮片部分的固结土壤的滑移半径比外轮片表面的滑移半径更大,如图12b所示,这在一定程度上增大了轮周的不平稳性。固结土壤的形状稳定性比金属轮周差,因此固结土的瓦解会使内轮片部分的固结土壤段的滑移半径不稳定,导致运动稳定性大大降低。同时,轮刺产生的滑移线Q′I′会覆盖一定区域的外轮片,这也会使滑移轮周的形状稳定性下降。因此滑移线的分布需考虑运动平稳性和形状稳定性。
由于滑移线平稳覆盖状态下的内轮片处滑移半径是由A点处断面和C点处轮刺这两处滑移线的对数螺旋部分共同组成的,且A、C两处的剪切要素倾角及对土壤的作用机理相同,所以,从3.2节的分析可以看出,滑移线平稳覆盖应优先考虑A点处断面的倾角大小设计,并使C点处轮刺的倾角与A点处断面的倾角保持相同大小即ψ=φ,如图13所示。

图13 断面处平稳连续滑移线模型
由图13可以看出滑移线,断面处的滑移线和轮刺处的滑移线各覆盖半个内轮片-土壤接触区,因此此时的滑移线覆盖轮片角β′=β/2,由表1可以看出,虽然仅存在断面时滑移线难以完全覆盖内轮片-土壤接触区,但存在断面和轮刺时,滑移线覆盖轮片角大小减半,使得内轮片-土壤接触区的完全覆盖成为可能,因此C点处的轮刺设计更为必要。不同倾角下的土壤流动滑移角对应的内轮片角β与轮扩角α之间的关系如图14所示,阴影区表示滑移线可完全覆盖内轮片-土壤接触区的范围。

图14 对数螺旋线对应的轮片角β′与轮扩角α的关系
由图14可以看出,平稳覆盖模式下存在无法完全覆盖的内轮片区域,并且随着倾角增加,滑移线覆盖区域越来越小;相同倾角状态下,图14中的完全覆盖轮扩角与图8中的完全覆盖轮扩角相同,而由于此时断面处的滑移线和轮刺处的滑移线各覆盖半个内轮片-土壤接触区,因此滑移线覆盖轮片角β′为图8中的滑移线覆盖轮片角β的一半。因此若要实现滑移线的平稳连续,需对剪切断面和可调轮刺的高度及倾角进行设计,由于C点处轮刺的倾角和高度与A点处断面的倾角和高度保持相同,因此需要综合设计断面或轮刺的倾角和高度。
图15所示为剪切断面高度和倾角与覆盖轮扩角的关系,可以看出,和倾角相比,轮刺高度的增加能显著地增大滑移线覆盖轮扩角,即提高滑移线对内轮片-土壤接触区的覆盖能力。虽然倾角可以增大土壤对变径轮的水平推力[14],但会缩小滑移线的覆盖区域;断面(或轮刺)的高度对滑移线覆盖轮扩角(对滑移线的覆盖区域)的影响更为显著。因此基于平稳滑移线覆盖的设计思路采取高度为主、倾角为辅的方法。图16所示为不同的变径比(轮径扩展长度为50~75 mm)下,满足平稳覆盖的断面倾角φ与高度h之间的关系。

(a)倾角φ的影响

图16 不同轮扩状态下倾角φ与高度h的关系
由表1和图12a可以看出,在倾角、高度相同的状态下,轮刺处的滑移线覆盖范围比断面处的大,因此平稳覆盖状态的实现主要取决于断面产生的土壤滑移线对断面至轮刺间内轮片-土壤接触区的覆盖程度。
表2所示为不同轮径扩展长度L下的变径轮几何参数,通过线性规划得到断面(或轮刺)高度h与倾角φ以及变径比η的函数关系式:

表2 不同轮径扩展长度L下的轮扩角
h=(0.273φ+23.37)(η-1)
(14)

表3 不同轮径扩展长度L下合适的断面(轮刺)高度
同时由表2可以发现,轮扩角的大小主要受轮径扩展长度L的影响,倾角对其影响相比较小;由表4可以发现,轮径和倾角增大时,轮刺高比λ也增大,但总体来看轮刺高比处于0.07 ~0.13之间。考虑到轮刺和断面属于实际轮径骤变位置,过大的轮刺和断面的高度会使轮片过厚,因此断面(或轮刺)高度h宜为0.1(r+L)。本文设计的轮径为100~175 mm,考虑最大轮扩状态下的完全平稳滑移线覆盖,断面和轮刺的高度选择18~22 mm、倾角小于20°较为合适。

表4 不同轮径扩展长度L下的轮刺高比
图17所示为存在轮刺和断面的变径轮在不同倾角情况下,满足平稳连续滑移线要求的轮周表面滑移半径(含固结土壤)的分布。

(a)实际轮周半径rc分布
同前所述,作为实际运动轮廓的滑移半径分布比实际轮周波动小。由图17可以发现:①倾角增大时,断面及轮刺高度需增大,以实现轮周表面的平稳连续滑移线覆盖。在保证最大轮径一定的前提下,内轮片的半径将缩小,从而增大实际的内外轮面差;含固结土壤的滑移半径最大值位于轮刺滑移线上,最小值位于断面滑移线与轮刺的交点处(参考图12点M′的位置)。②倾角增大使得断面处的土壤滑移线在轮刺处的高度减小,从而增大轮刺处的滑移线半径差。③倾角增大会显著减小轮刺滑移线的最大半径,提高滑移半径的运动平稳性和形状稳定性。
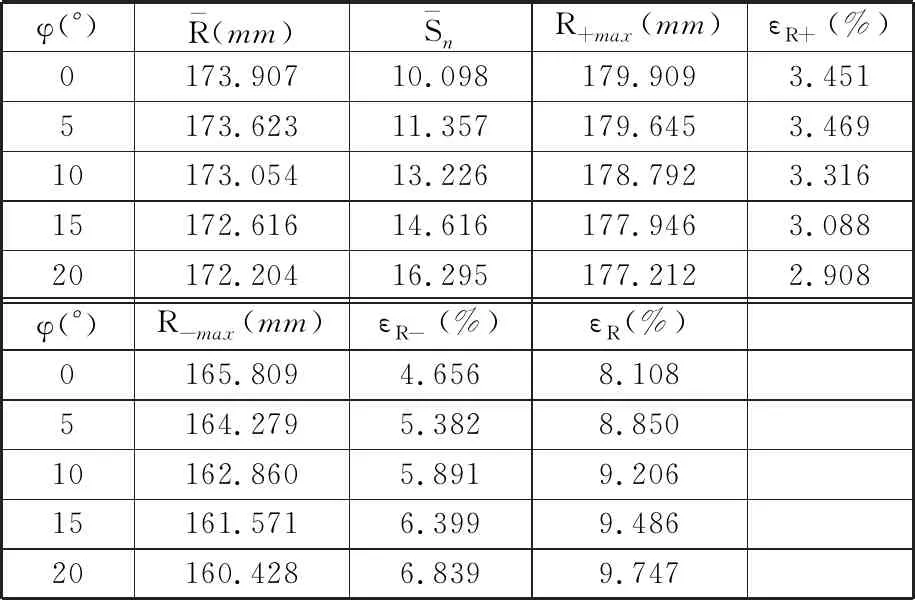
表5 不同倾角状态下轮周滑移半径分析

4 结论
(1)从土壤剪切滑移线的角度分析,提出了两种滑移线分布的概念:完全连续滑移线分布和连续平稳滑移线分布。所设计的双层轮片变径轮(最小变径轮径为100 mm,最大变径轮径为175 mm)结构,依靠扩展状态下内外轮片的剪切断面可以实现对内轮片与土壤接触区的完全连续滑移线覆盖;若要实现该土壤接触区的完全连续且平稳滑移线覆盖,则需在内轮片中部设计可调轮刺。
(2)变径轮在内轮片中部处设计有可调轮刺时,内外轮片断面和轮刺的倾角要相匹配,倾角小于20°既可以增大变径轮的水平推力,又可实现内轮片与土壤接触区的完全连续滑移线覆盖。
(3)考虑仅存在对数螺旋滑移线部分的平稳连续滑移线模型,提出了变径轮断面和相匹配的轮刺设计应以高度为主、角度为辅的设计思想。在内轮片与土壤接触区的滑移线满足完全连续覆盖且平稳分布的条件下,显著提高了变径轮的运动平稳性和形状稳定性,并确定了变径车轮断面(或可调倾角轮刺)高度h、倾角φ与变径比η之间的函数关系。
(4)滑移线完全连续且平稳覆盖的前提下,倾角不大于20°时,轮周表面各点处滑移半径平均值波动不大,因此无需考虑断面(或轮刺)的倾角φ和高度h对轮周滑移半径波动的影响,即运动稳定性和形状稳定性无明显差别。

