牙轮钻头用单金属密封瞬态启动动力学模型与密封性能

马 艺 陈宇涛 孟祥铠 赵文静 彭旭东

1.浙江工业大学机械工程学院，杭州，3100232.过程装备及其再制造教育部工程研究中心，杭州，310023

0 引言

牙轮钻头是我国油气勘探开发常见的破岩工具，适用于深部、超深部等地层。单金属密封因结构简单、耐磨损、占用空间小等特点，被广泛应用于牙轮钻头轴承密封系统，在确保钻头长期使用方面起着关键作用。受钻井环境、操作工况、地层特点及不可控因素等综合影响，牙轮钻头在破岩钻进过程中存在频繁启停现象，同时伴随有剧烈振动[1-3]，尤其是在高压条件下，单金属密封的动态稳定性对牙轮钻头乃至整个钻采系统的可靠性和安全性至关重要[4],因此，有必要开展启动过程中牙轮钻头单金属密封受振动激励的瞬态动力学行为及密封性能的研究。

国内外学者主要对钻头金属密封的稳态性能和结构优化开展了相关研究。张毅等[5-6]利用有限元分析方法对第二代单金属密封(SEMS2)进行热力耦合研究，分析了井下温度和钻井液压力等对密封端面接触压力和泄漏率的影响，并以此为基础开展了单金属密封的多目标优化。ZHOU等[7]和ZHANG等[8]研究了双金属密封的接触力学性能及压差、压缩比和热负荷等对密封的影响，综合分析了O形辅助密封圈的应力分布及变形状态。马艺等[9]基于密封系统的热-流-固多场耦合状态建立了单金属密封(SEMS2)稳态综合数学模型，研究了密封端面膜厚、温升等随运行工况的演化规律。目前对钻头密封动力学行为的研究较少，XIONG等[10-11]针对第一代单金属密封(SEMS)建立了混合润滑状态下的非轴对称数值模型及不考虑温度和端面变形情况的动力学模型，研究了密封端面液膜压力、厚度及泄漏量的时变特性，结果表明单金属密封瞬态泄漏率、接触应力等明显增加。相对较为成熟的机械密封动力学分析思路和方法可在一定程度上为单金属瞬态密封性能的研究提供借鉴。GREEN等[12]构建并求解了接触式机械密封的润滑控制方程和动力学方程，探究了密封环受轴向振动和跳动时的瞬态运动规律。孟祥铠等[13]建立了描述机械密封瞬态启停过程的动力学模型，研究了启停过程中轴向跳动对机械密封浮动环动态特性的影响。徐鲁帅等[14]建立了复杂扰变工况下非接触式机械密封动态耦合数学模型，分析了变速及扰动下机械密封的瞬态响应及振动特性。

综上所述，目前关于钻头密封的研究尚未充分考虑瞬时启动与振动工况对牙轮钻头单金属密封性能的影响，而且单金属密封的动态特性与密封端面液膜状态的耦合作用机制尚不明晰。本文建立牙轮钻头单金属密封(SEMS2)瞬态特性综合数学模型，探究瞬时启动及振动工况下单金属密封的动力学行为与密封性能，考察钻头转速、轴向激励对单金属密封端面液膜形态、端面温升及泄漏率、摩擦扭矩时变特性的影响规律，为钻头金属密封系统的高效可靠设计提供参考。

1 计算模型

1.1 几何模型

图1为牙轮钻头单金属密封装配结构示意图。单金属密封系统由金属动环、金属静环、O形圈、橡胶支撑环及轴颈组成，利用O形圈等辅助密封件的弹性支撑作用使金属静环与金属动环紧密贴合。密封环内径侧介质为润滑油，外径侧介质为钻井泥浆，两侧密封腔保持一定压差(Δp=0.3～0.7 MPa[15])，以防止泥浆侵入轴承。

1.金属动环 2.润滑油 3.O形圈 4.金属静环 5.钻井泥浆 6.橡胶支撑环 7.轴颈

1.2 数学模型

单金属密封的端面润滑特性、热传递、端面变形和动态特性之间存在强耦合关系，因此，需综合开展流体力学、接触力学、传热学与动力学分析，从而建立单金属密封瞬态特性综合数学模型。

1.2.1端面润滑

根据单金属密封工作环境，作以下假设：①密封介质为牛顿流体；②金属密封环为轴对称模型，忽略周向变化；③忽略空化、惯性力对密封环的影响。

充分考虑表面粗糙度、挤压效应、流量因子及接触因子等影响，建立适用于单金属密封混合润滑状态的控制方程：

(1)

式中，r为径向位置；μ为液膜动力黏度；h为液膜厚度；pL为液膜压力；t为时间；φr、φc分别为径向流量因子和接触因子[16]。

径向流量因子φr采用下面经验公式计算：

(2)

式中，γ为平面的表面特性，表示微凸体在x方向和y方向的数值比；C、λ分别为与γ相关的系数；σ为密封端面综合粗糙度的均方根。

不失一般性，采用γ=1时的各项系数值，径向流量因子φr可表示为

φr=1-0.9exp(-0.56h/σ)

(3)

接触因子φc可表示为

(4)

由于温度开高，流体性质发生明显变化，故采用如下方程表征温度T对流体黏度的影响[17]：

μ=μ0(T0/T)β

(5)

式中，T0为环境温度；μ0为环境温度下的流体黏度；β为黏温系数。

1.2.2热分析

单金属密封的热源主要来自两方面：①动静环相对转动，端面间接触部分产生接触摩擦热qf；②密封环对端面间液膜的黏性剪切作用，产生黏性剪切热qv。热流密度q的计算公式为

q=qf+qv

(6)

qf=fpcωr

(7)

(8)

式中，f为动摩擦因数；ω为动环旋转角速度；pc为接触压力。

假设微凸体高度呈高斯分布，则接触压力可表示为[17]

(9)

式中，H为端面材料的压缩强度。

忽略热滞后，利用影响系数法[18]对端面温度的变化进行求解。端面节点i处的温度Ti表达式为

(10)

Ti=T0+δTi

(11)

式中，Tij为温度影响系数，代表单位热量作用在节点j时节点i处的温升；qj为不同节点j处的热流密度；δTi为节点i的温度变化。

1.2.3端面变形

液膜压力和接触压力分布都与膜厚密切相关，接触压力又强烈地依赖于密封面的热、力变形。由于密封环端面变形非常小，故假定变形与作用力和热流量成线性关系，采用影响系数法[18]求解端面变形量。利用ANSYS软件建立单金属密封有限元模型，分别对动静环端面各节点施加单位力载荷和单位热流量，组成力变形影响系数矩阵和热变形影响系数矩阵，则节点i处两个密封面的组合变形δi可表示为

(12)

式中，Lij、Rij分别为单位力、热载荷作用在节点j时节点i处的变形量；Fj为作用在节点j上的力；Ci为环境压力下钻头未启动时节点i处的初始变形量。

膜厚分布可由如下方程获得：

hi=hm+(δir+δis)max-(δir+δis)

(13)

式中，hm为不同时刻下的初始膜厚值，即平均膜厚；δir、δis分别为动静环在节点i处的绝对变形量；(δir+δis)max为动静环绝对变形的最大代数和；(δir+δis)为动静环在节点i处的代数和。

1.2.4动态分析

钻头瞬态启动及振动条件下，单金属密封所受载荷不断变化，静环位置通过辅助密封件动态反馈调节，端面膜厚随之变化。对单金属密封系统动静环进行简化及受力分析，如图2所示。

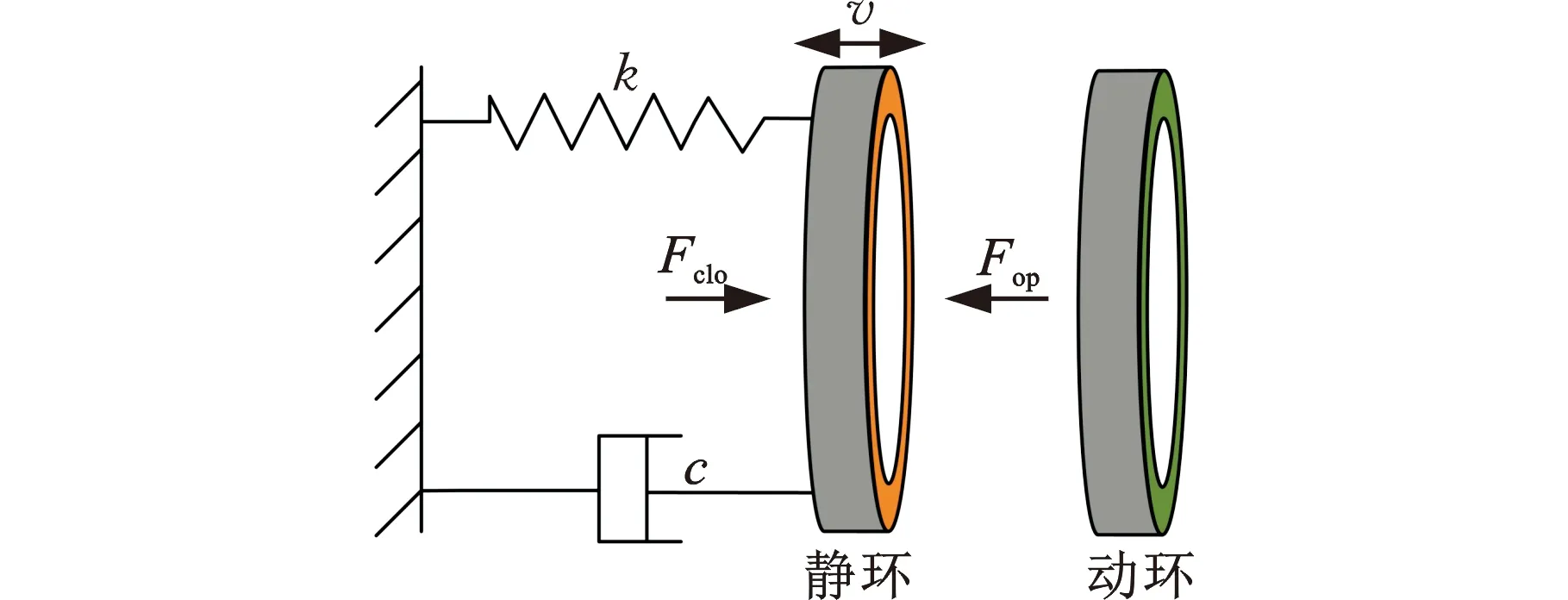
图2 动力学分析示意图

建立轴向扰动作用下金属静环的动力学方程：

(14)

式中，m为金属静环质量；k为辅助密封元件的轴向刚度系数；c为辅助密封元件的轴向阻尼系数；Fclo为闭合力；Fop为开启力；Fa为振动引起的轴向载荷。

闭合力由内外介质压力及辅助密封件对金属静环的作用共同组成，即静接触压力psc对密封端面的作用力，计算公式为

(15)

式中，ri为密封环内径；ro为密封环外径。

开启力由接触力Fc和液膜力FL共同组成，可表示为

Fop=FL+Fc

(16)

(17)

(18)

对于振动引起的轴向载荷，因载荷频率f与角速度ω有关，即f=ω/(2π)，故假定波动为正弦形式[19]，则有

Fa=Asinωt

(19)

式中，A为载荷幅值。

采用Newmark法中的平均加速度法逐步积分求解上述动力学方程[20]。在每一时间步，采用二分法求得当前时间步的密封性能参数和动力学特性参数，并为下一时间步的计算提供初始值。计算公式为

(20)

(21)

式中，α=0.25；γ=0.5。

1.3 计算流程

瞬时启动过程单金属密封动力学特性的计算流程如图3所示，采用有限差分法结合多重数值迭代算法进行联合求解。

2 计算参数及模型验证

2.1 计算参数

本文计算的基本参数[21]如表1所示。

表1 单金属密封几何参数及工况参数

启动阶段钻头所处环境压力不变，角速度随时间变化采用定加速度线性增加的方式实现[22]，表达式为

(22)

式中，ωend为启动时最终角速度；ta为加速时间。

钻头启动过程中角速度ω和激励载荷Fa的变化规律如图4所示。t=0～1 s为启动阶段，角速度以线性形式增加，激励载荷频率随角速度ω逐渐增大；t=1～2 s为恒转速阶段，转速和激励载荷频率保持不变。当t>2 s时，单金属密封继续保持上述恒转速稳定波动状态，为更直观地体现单金属密封瞬时启动阶段各参数变化，后续均截取前2 s时间段开展分析。

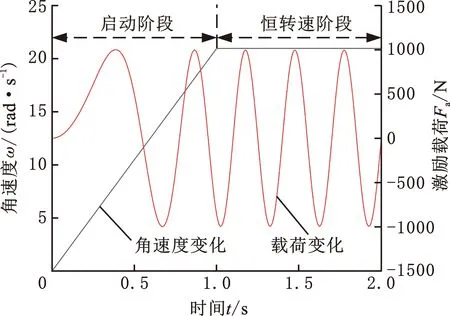
图4 启动过程角速度和激励载荷变化规律

2.2 模型验证

为验证本文瞬态模型和方法的准确性，采用文献[23]中的参数进行数值计算，并将计算结果与文献中结果进行比较，分析多个时刻(t=1，5，10，20 s)密封端面液膜压力与厚度的分布规律，如图5所示。结果表明，4个时刻本文模型所得液膜压力pL和液膜厚度h的径向分布趋势与文献[23]所得趋势均一致。本文计算值与文献值吻合较好，整体上略小于文献值。由图5可知，本文模型所得密封端面液膜压力、液膜厚度和文献值的相对误差均在t=20 s时、径向位置r=60.8 mm处达到最大，分别为7%和9%。因此，本文建立的综合数学模型能够较好地预测启动瞬时密封系统的动力学特性。

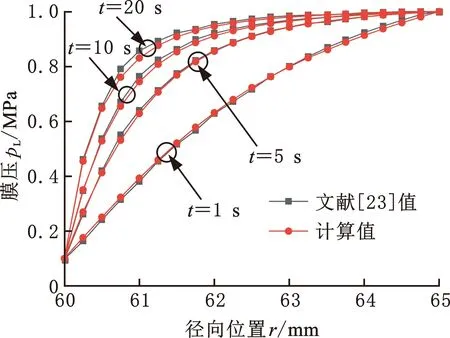
(a) 液膜压力对比

3 结果分析和讨论

3.1 启动过程单金属密封动态特性

3.1.1液膜演化规律

图6为启动过程中单金属密封端面液膜厚度三维分布及时变曲线。由图6a可以看出，在初始t=0时刻，密封端面膜厚沿径向逐渐增大，呈发散型密封间隙。这是因为受高压下静环内侧O形圈变形影响，单金属密封端面接触压力呈内径侧高外径侧低的分布趋势。联合式(4)分析可得，密封区域内径处膜厚值最小(0.248 μm)且h<3σ，微凸体会发生接触，处于混合润滑状态；外径处膜厚值最大(0.381 μm)且h>3σ，处于流体润滑状态。瞬态工况下密封端面发散型膜厚分布趋势保持不变，但膜厚数值不断变化。由图6b可以看出，在t=0～1 s启动阶段，端面最大、最小膜厚波动频率逐渐增加，波动幅度受转速增加和载荷激励影响扰动明显。之后在t=1～2 s恒转速阶段，端面膜厚均呈周期性正弦形变化，静环在闭合力、开启力和轴向激励载荷的共同作用下逐渐达到动态平衡，密封端面形成相对稳定的楔形振荡间隙，但密封间隙内流体状态始终为层流。相对而言，恒转速阶段密封端面最大膜厚的振幅可达最小膜厚振幅的2倍，容易加剧润滑油的泄漏。

(a) 膜厚三维分布

选取初始t=0时刻(t0)及各特征波峰波谷(t1～t5)作为代表性瞬态时刻(图6b)，分析不同时刻下单金属密封端面液膜压力(简称“膜压”)与接触压力的径向分布，如图7所示。t0时刻密封端面膜压沿径向线性减小，与膜厚分布呈相反趋势。随着钻头的启动以及激励载荷的不断作用，密封端面径向膜压分布逐渐演变成“上凸”—“下凹”—“上凸”的循环变化模式。在转速稳定后，端面膜压保持周期性变化且波动幅值更大，尤其在径向位置r=32.4 mm处膜压振幅最为明显，最高可达7.7 MPa。这是因为持续的激励载荷使得液膜受到挤压作用，当密封环相互远离时，膜压减小，反之膜压增大。由图7b可知，不同时刻下接触压力始终在密封环内径处(r=31 mm)达到最大值，尤其在启动过程中(t1时刻)可达18.6 MPa，而在外径侧，由于微凸体不直接接触，密封环完全由液膜压力承载，因此，启动过程中单金属密封内径侧润滑油难以顺利进入密封间隙，润滑状态进一步恶化。

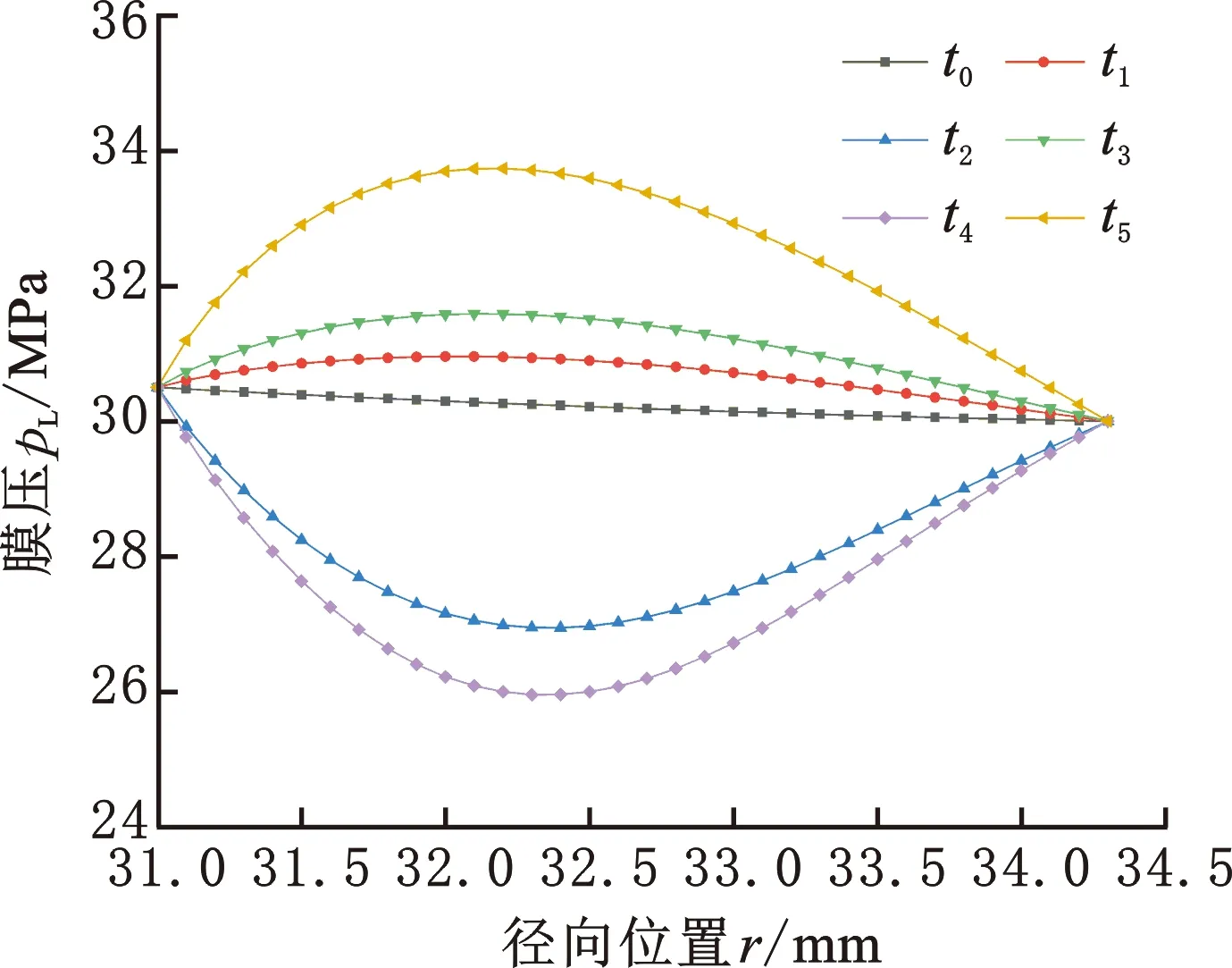
(a) 液膜压力

3.1.2温升时变特性

图8为启动过程中单金属密封端面温升ΔT时变曲线和瞬时温升径向分布曲线。可以看出，初始t0时刻密封端面温度为环境温度T0。密封端面温升在钻头启动阶段呈波动增长趋势，并在进入恒转速阶段后振荡幅值差异性更加明显，端面最大温升振幅达到最小温升振幅的2.3倍。因端面内径处始终承受大部分接触压力，而外径处接触压力为0，所以各时刻端面温升在靠近内径侧(r=31.4 mm)和外径处分别达到最大、最小值，在恒转速t5时刻端面径向温差可达5.5 K。

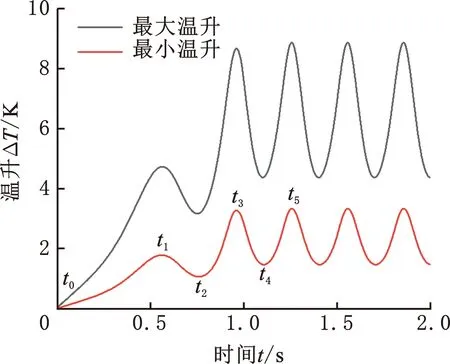
(a) 最大、最小温升

图9为不同时刻密封动静环整体温度分布云图。以密封环端面最大温升所在径向位置r=31.4 mm为中心，随着热量向密封环主体不断传递，动静环温度逐渐降低，最低温度位于动环与牙轮钻头的接触边界，基本与环境温度持平。静环相比于动环整体温升更为明显。

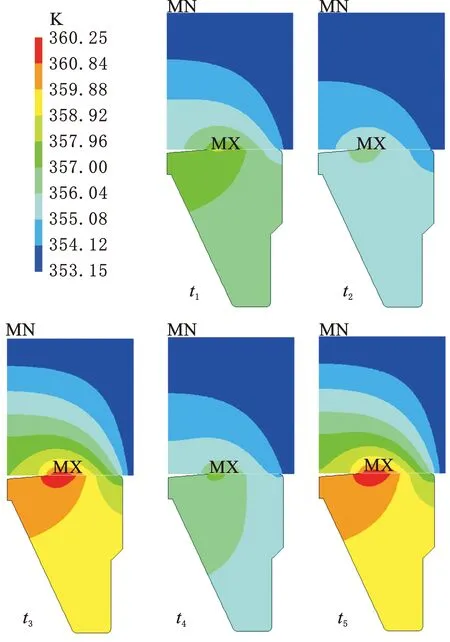
图9 密封环温度分布云图

3.1.3动态密封性能

图10所示为启动过程中单金属密封泄漏率与摩擦扭矩的变化规律。钻头启动瞬时摩擦扭矩发生阶跃性变化，并逐渐波动至振幅约为5 N·m的相对稳定状态。随着钻头的启动，单金属密封泄漏率的振动频率和幅值逐渐增大，且远超稳态泄漏率(0.0135 mL/h)。原因在于，一方面转速的提高导致端面温升逐渐增加，润滑油黏度下降；另一方面受到轴向激励的影响，密封端面外径侧液膜压差增大，对密封端面间液膜产生挤压效应。在启动和恒转速阶段，泄漏率均呈正负交替的波动状态：泄漏率为正值时，密封内径侧的润滑油向外径侧泄漏；泄漏率为负值时，密封外径侧的泥浆极易侵入密封间隙。即振动工况下单金属密封端面磨损加剧，更易失效，进而影响牙轮钻头的使用寿命。

图10 泄漏率和摩擦扭矩随时间的变化规律

3.2 钻头转速对密封动态特性的影响

保持启动转速趋势不变，研究钻头最终稳定转速n分别为100，200，400，600 r/min时单金属密封端面平均膜厚和最大温升的变化规律，如图11所示。由图11a可以看出，随着钻头转速的增加，启动和恒转速阶段密封端面平均膜厚波峰值保持不变，而振动幅度逐渐减小且频率明显增加。这是因为当转速增大时，端面膜厚沿径向发散程度增加，液膜承载能力提高，使得密封环在相同的激励下更快进入稳定振动状态。即适当增加转速，可改善密封界面润滑状态，提高密封稳定性。密封端面最大温升始终靠近内径侧(r=31.4 mm)，但数值及变化梯度变化明显。由图11b可以看出，密封端面间的接触摩擦热和黏性剪切热随转速增大而增加，启动阶段端面最大温升整体大幅波动攀升，至恒转速阶段后振动频率和幅度均明显增加，钻头转速n=600 r/min时的振动幅值约为n=200 r/min时振动幅值的3倍。

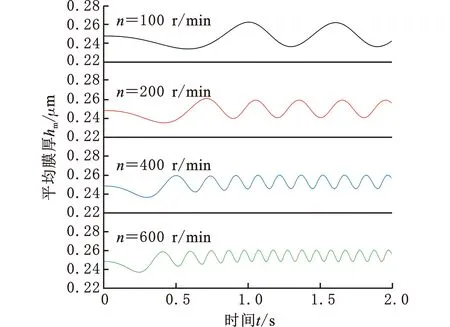
(a) 平均膜厚

图12为不同钻头转速下单金属密封泄漏率和摩擦扭矩的时变曲线。由图12a可以看出，在启动初步阶段，低转速下密封界面泄漏率变化缓慢；随着转速不断增加，密封端面介质黏度降低，泄漏率振动频率和幅值逐渐增加，至恒转速阶段后，转速n=600 r/min的瞬时最大泄漏率增至n=200 r/min的2.5倍。由图12b可以看出，低转速启动时，摩擦扭矩振幅随转速变化并不明显，而在n≥400 r/min时，摩擦扭矩幅值随着转速增大逐渐减小。这与钻头转速增加所导致的膜厚增大有关，密封端面间特别是内径处接触压力的减小使得摩擦扭矩降低。

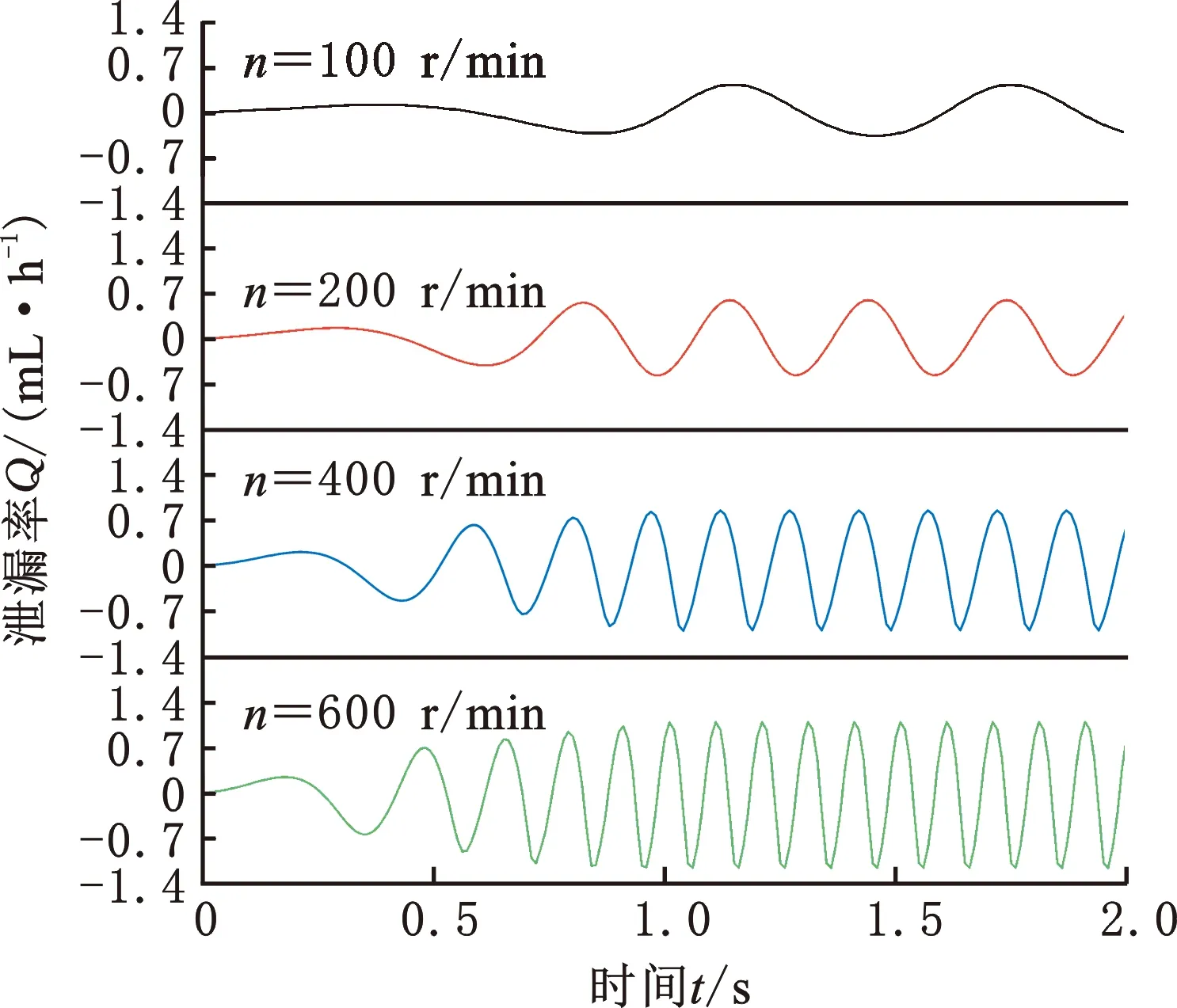
(a) 泄漏率

3.3 轴向激励对密封动态特性的影响

研究轴向激励载荷Fa分别为500，1000，500，2000 N时单金属密封端面平均膜厚和最大温升的变化规律，如图13所示。可以看出，不同激励载荷下密封端面平均膜厚和最大温升的振动频率及所处径向位置均保持不变，单金属密封的稳定性相对较好。在启动阶段，平均膜厚振幅随轴向激励载荷增大而明显增大，且因惯性作用，它与恒转速阶段振幅差异更加明显。由于动静环贴合瞬间摩擦热增加，端面最大温升振幅随轴向激励载荷增大呈振荡递增至稳定的变化趋势。在恒转速阶段，端面平均膜厚和最大温升波形均随轴向激励载荷增大而上移，这是因为高激励载荷作用下密封环接触压力和力变形增大所致。

(a) 平均膜厚

图14为不同轴向激励载荷下单金属密封泄漏率和摩擦扭矩的时变曲线。可以看出，随着轴向激励载荷增大，泄漏率和摩擦扭矩的波动幅值随之增至稳定，此时Fa=2000 N时的最大泄漏率和摩擦扭矩可达Fa=500 N时的4.1倍和1.8倍。在恒转速阶段，泄漏率仍呈正负对称交替式变化，而摩擦扭矩曲线则随轴向激励载荷增大而上移，这与密封端面平均膜厚变化相对应。因此，轴向激励对单金属密封动态稳定性影响显著，进而影响牙轮钻头的可靠工作。

(a) 泄漏率

4 结论

(1)高压(p0=30 MPa)下单金属密封端面液膜沿径向呈发散型间隙分布，由内径侧的混合润滑状态逐渐过渡为外径侧的流体润滑状态；钻头启动至恒转速过程中，端面膜厚波动频率逐渐增加，最终稳定呈周期性正弦型变化，且液膜发散程度随钻头转速增加而增大，液膜承载能力有所提高。

(2)钻头启动时单金属密封端面温升振荡增加，径向温升变化梯度逐渐增大，分别在靠近内径r=31.4 mm处和外径处达到端面最大和最小温升；随着转速和轴向激励载荷增大，密封端面间接触摩擦热和黏性剪切热增加，端面温升波动振幅明显增大。

(3)在钻头启动和振动共同作用下，高转速启动时的摩擦扭矩幅值随转速增大逐渐减小；单金属密封瞬时泄漏率呈正负交替波动状态，幅值远大于稳态泄漏率，特别是当泄漏率为负值时，密封外径侧的泥浆极易侵入密封间隙，而且该现象随钻头转速和轴向激励载荷增大显著加剧，单金属密封性能进一步恶化。