非同轴前后轮自平衡车非线性转弯平衡控制

董慧芬，宋金海

(中国民航大学电子信息与自动化学院，天津 300300)

1 引言

当今机器人快速发展，各式各样的机器人琳琅满目，医疗机器人、服务机器人、仿人机器人、平衡机器人等等[1-3]。目前平衡机器人是国内外的研究热点，随着传感器技术和微控制器技术发展，其中非同轴前后轮机器人因为其简单结构、成本低廉、能在地势起伏较大的情况下仍能保持良好的性能，成为了当前平衡机器人的主流[4-5]。由于该机器人是一种具有强耦合、欠驱动的非线性系统[6]，关于其动力学建模和提出新的控制方法引起了许多学者的兴趣。Ham等人提出了一种简单的自行车机器人的动力学模型，在此基础上设计了一个内部平衡控制器[7]；密歇根大学的Anouck等制作了非同轴的两轮小车，利用拉格朗日方程分别建立了单陀螺和双陀螺动力学模型[8]，在平衡点附近进行简单地线性化，对线性化后的模型进行控制和分析，但是由于其线性化过于粗略，无法实现较大倾角的回正。武汉理工大学的赵燕教授对双陀螺的非同轴前后轮机器人采用拉格朗日进行动力学建模[9]，设计了滑模控制器进行机器人的平衡控制，但是对于该机器人的转弯动力学模型没有深入研究；俄亥俄州立大学的Harun Yetkin 等人研发了一种基于陀螺进动效应的自平衡车[10]，采用 Lagrange 方程建立自平衡车的动力学模型，设计了一阶滑模控制器和 PID 控制器，试验表明滑模控制器的效果比 PID 控制器效果好，但其采用的单陀螺布局会产生干扰自行车俯仰或者偏航运动的力矩，在自行车转弯过程时由于单陀螺布局容易导致侧倾发生，无法完成转弯运动。2015年吕宽洲等人设计一款带有陀螺装置的无人自行车[11]，通过设计平衡控制算法直接作用于陀螺，产生陀螺力矩维持自行车平衡，实现了无人自行车在静止状态能自动恢复到竖直状态，但对于受到撞击干扰等能否快速恢复到平衡状态没有进行深入展开。北京凌云智能科技公司提出了一种基于陀螺效应的两轮电动车的概念车[12]，其通过驾驶者人工控制方向盘和陀螺产生的陀螺力矩来平衡重力矩，维持两轮汽车在行驶过程保持平衡状态，没有进行自平衡的无人自动控制方面的研究。

根据上述国内外对于非同轴前后轮机器人的动力学建模和控制器的研究，主要的侧重点都在于车体在直线运动或者静止时的自平衡控制方面，对于机器人的转弯动力学建模、一定转向角下平衡车的姿态控制没有深入的研究。因此本文在建立平衡车转弯动力学非线性模型的基础上，采用反馈线性化方法进行非线性模型的线性化，而不是在平衡点附近的线性化处理，对前后轮平衡车转弯控制进行研究，减小线性化误差的影响。

2 非同轴前后轮平衡车转弯动力学建模

2.1 陀螺平衡原理

本文中非同轴前后轮平衡车采用陀螺作为平衡单元，如图1所示，陀螺自转轴为y轴，进动轴为Z轴。陀螺绕着自转y轴以w0的角速度进行自转，陀螺相对于y轴转动惯量是J0，当陀螺绕着Z轴以角速度进动时，根据右手定则陀螺将会产生一个沿着X轴方向的力矩M。

图1 陀螺力矩产生原理

由于进动角度的产生，陀螺力矩的方向会改变，可以分解为偏航力矩和倾斜平衡力矩，前者是影响平衡车方向的干扰力矩，后者是平衡倾斜姿态的力矩。所以文中采用双陀螺平衡方案，为了让偏航力矩抵消、平衡力矩叠加，要求两个陀螺的自转方向和进动方向都相反，如图2。

图2 双陀螺平衡原理

2.2 自平衡车转弯原理分析

当平衡车进行转弯时，会产生一个使平衡车侧翻的离心力，通过改变车身的倾斜与车身的速度可使平衡车不产生侧倾。利用这一现象，对平衡车一定倾斜角下的转弯动力学分析，图3(a)为平衡车后视简化图，图3(b)为车身侧倾一个角度进行转弯运动力学分析，其中，O为平衡车的重心，G为平衡车的重力，FN为地面对平衡车的支撑力，f为前后轮所受的摩擦力，h为平衡车质心离地面的高度。

图3 平衡车转向力学分析示意图

由图3(a)可知，平衡车在向右进行转向时，受到与转向方向相反的一个摩擦力f，导致平衡车在转向时候向左翻转。图3(b)是通过平衡车倾斜一定角度β，转弯所需的向心力由车体倾斜产生的分力提供，车体便不会发生倾倒。所以转向时的向心力与自平衡车的横滚角之间存在着耦合关系。如下式(1)

fh=FNhtan(β)

(1)

由式(1)可知

f=Gtan(β)

(2)

平衡车转弯示意图如图4所示，表示平衡车的转向角，L为平衡车前后轮心间距，O为平衡车的转弯圆心，R为转弯半径，v为平衡车前进线速度，则平衡车转弯所需要的向心力为F向心力=2mv/R。

图4 平衡车转向俯视图

假设机器人所提供的最大静摩擦力等于所需要的向心力，则机器人倾斜角β与转弯半径的表达式如式(3)

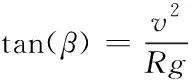
(3)

根据正弦定理可知

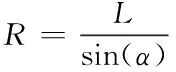
(4)

式(3)与(4)可知平衡车平稳地进行转弯运动需要对倾斜角与车身的速度进行协调控制，下面将对平衡车转向动力学进行建模。

2.3 自平衡车的转弯动力学模型

将前后轮平衡车系统可以看作由三个刚体部分组成：车体、高转速的陀螺、前后轮。以β表示平衡车的倾斜角，α表示平衡车的转向角，θ表示陀螺的进动角。如下图5(a)和图5(b)所示，车轮的质量为m1且半径为r1，车体的重量为m2、质心高度为h1，车体沿经过前后轮直线的转动惯量为Ib。陀螺的质量为m3，质心高度为h2，自转轴的转动惯量为Jr，沿着x轴的转动惯量为Jp。假设平衡车初始线速度为v0，车轮和车体有2个方向的运动，分别是平动和倾斜方向。

图5 平衡车结构简图

从上述假设和平衡车参数可知平衡车的动能

T=Tb+Tg+Tf+Tw

(5)

不考虑其它不确定的外部干扰，系统的所受广义力中重力为有势力，则系统的势能为

V=2m1gr1cosθ+m2gh1cosθ+2m3gh2cosθ

(6)

对于广义坐标β，受到的非有势广义力矩为

(7)

其中α为平衡车的转角，Wd为后轮驱动电机的功，L是前后轮着地点的间距。

对于广义坐标θ，受到的非有势广义力矩为

(8)

其中Tt为进动电机的力矩。

对于广义坐标α，受到的非有势广义力矩为

(9)

其中Twh为转向电机的力矩，μ转向架与车体的摩擦系数。

选取平衡车的倾斜运动陀螺进动两个自由度为系统的广义坐标，对于广义坐标β通过拉格朗日方程可以的到

+2sinθcosθ(Ip-Ir)-g(m2h1+m3h2)sinβ=

(10)

对于广义坐标θ通过拉格朗日方程可得

(11)

对于广义坐标α通过拉格朗日方程可得

(12)

设

u1=wd，u2=Tt，u3=Twh

由上式(10)-(12)可得平衡车的非线性转弯动力学模型如式(13)所示

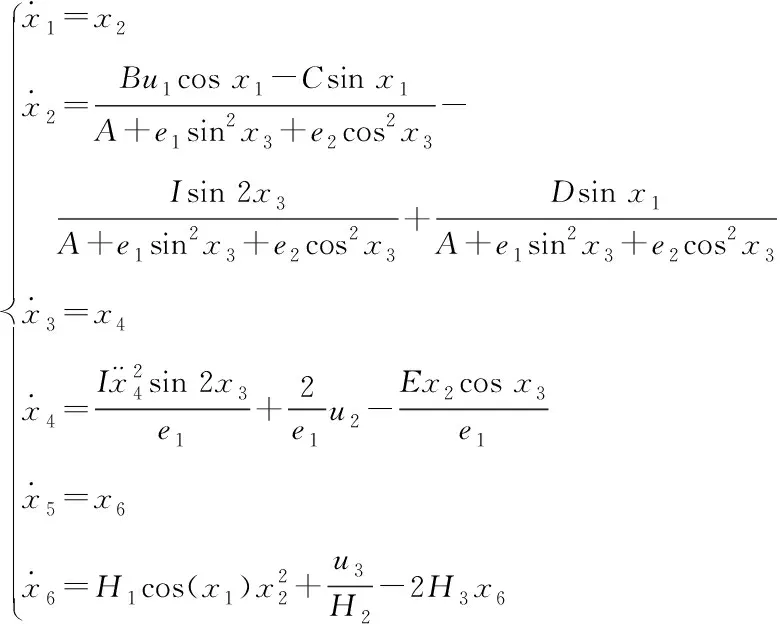
(13)

其中

C=(2m1r+m2h)g，D=g(m2h1+m3h2)，E=2Ipw

I=Ip-Ir，e1=Ip，e2=Ir，

3 自平衡车转弯非线性动力学模型反馈线性化

将平衡车的转弯动力学模型式(11)转化为矩阵形式，可以得到下面MIMO非线性模型

(14)

其中，x∈R6，u∈R3，y∈R3，f(x)为6维的光滑的向量场，G(x)是6*3的矩阵，具体如下公式

H(x)=[h(x1)，h(x2)，h3(x3)]

x=[x1，x2，x3，x4，x5，x6]，y=[y1，y2，y3]

G(x)=[g1(x)，g2(x)，g3(x)，g4(x)，g5(x)，g6(x)]

u=[u1，u2，u3]T

可以得到如下的矩阵

该矩阵在平衡点x0=(0，x2，0，x4，0，x6)T的邻域非奇异，所以系统在此邻域总相对阶为6阶，则有

其中v=[v1，v2]为新输入向量。由A-1(x)存在可得

(15)

通过状态反馈控制率得到非线性系统的线性化和对于新输入的解耦，在结合控制率对上述的等效线性系统进行研究。平衡车的线性化控制结构框图如图6所示。

图6 转弯非线性动力学模型线性化控制结构框图

4 基于反馈线性化转弯平衡控制仿真及结果分析

对于前后轮自平衡车，应用经过反馈线性化后的转弯动力学模型，设计PID控制器，可使小车的倾斜角快速稳定到达给定值。基于Matlab中Simulink搭建如图6所示仿真模型，根据实验平台准确估计获取小车模型参数如表1。

表1 平衡车参数

根据前面的公式计算得到A、B、C、D、E、I、e1、e2的值(其中g=9.8m/s2)，搭建Simulink模型进行仿真验证。下面实验分析图中虚线均为车身的倾斜角，实线为给定倾斜角的输入。

4.1 未使用反馈线性化解耦控制仿真结果分析

仿真中，为了探究在转向过程中平衡问题，在模型未进行反馈线性化的前提下使用PID控制器进行转弯控制，给定输入车速为1m/s，外部干扰力为0，在运动2s后给定转向角度为30°，根据式(3)，需要车身倾斜角保持在6°。

如图7所示，虚线为期望的转向角，实线为实际转向角。在平衡车运动过程中，在0s时输入一个幅值为30°的单位阶跃信号作为转向角度的输入，由图可知实际的转向角无法达到预期要求。

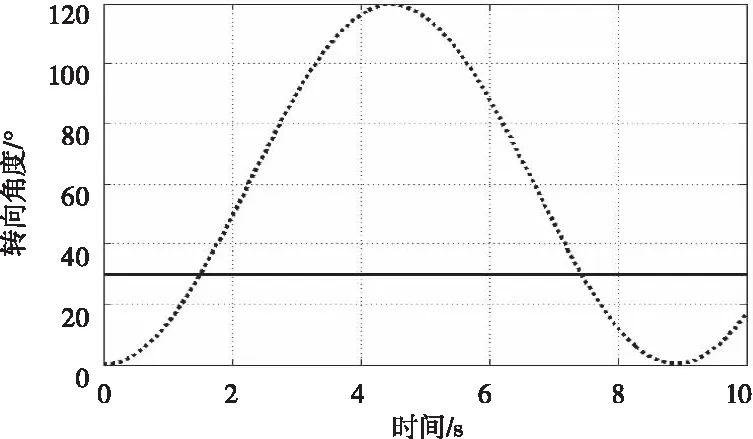
图7 普通pid控制器下α的响应

如图8所示，由陀螺的进动原理可知，由于陀螺的进动角一直在变化结果导致平衡车的倾斜角随之改变。

图8 普通pid控制器下θ的响应

如图9所示，平衡车不断地在-5°到-20°之间晃动，无法达到预期的6°。在实际中意味着平衡车无法在转弯时保持自身的平衡，无法完成转向过程。

图9 普通pid控制器下的β的响应

4.2 使用反馈线性化转弯控制仿真结果分析

将非线性的转弯系统进行反馈线性化后，加入PID控制器保持车身速度1m/s，在0s时输入一个幅值为30°的单位阶跃信号作为转向角度的输入。

如图10所示，平衡车在1s内转向角度达到预期的30°，超调量为0。

图10 使用反馈线性化解耦控制的α的响应

根据上面的式(3)，车身的倾斜角度需要到达6°，在下图11中在2s内达到预期倾斜角度，与上式(3)一致。

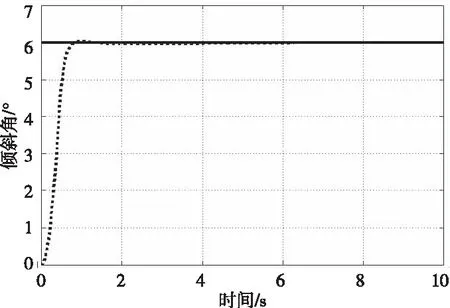
图11 使用反馈线性化解耦控制的β的响应

图12中陀螺的进动角在在0-2s时，产生进动效应对车身的倾斜角进行改变，在2-3s时，由于车身达到预期的倾斜角度，进动角的变化趋于0并且回复初始位置。

图12 使用反馈线性化解耦控制的θ的响应

4.3 抗干扰仿真结果分析

在保持一定倾斜角稳定转弯运行时，为了模拟受到碰撞等瞬时外部干扰，如下图13所示，在5s时刻加入一个大小为100N，持续时间为0.1s的干扰力。

图13 外部干扰力

仿真结果如图14所示，在受到外力干扰下，平衡车的转弯平衡状态受到打破，倾斜角度由稳态的6°变为最大值7.6°，经过3.9s回复到原来稳态值6°。由图15可知，陀螺的进动角发生变化，最大值为2.4°，产生进动力矩使平衡车在3.6s内回复平衡状态，进动角稳态误差为0，由此可知在一定干扰下平衡车能快速回复，保持自身的平衡稳定。

图14 干扰仿真倾斜角变化曲线

图15 干扰仿真进动角θ变化曲线

5 结论

本文以自平衡车车体左右倾斜角、陀螺进动角和转向角为广义坐标，利用拉格朗日法建立平衡车转向的MIMO仿射非线性动力学模型；提出一种基于非线性动力学模型的转弯平衡控制方法。仿真分析结果可知，采用基于反馈精确线性化理论设计的控制器，可以实现双陀螺平衡车的转弯平衡控制。在转向角30°和速度为1m/s的情况下，该平衡车可以在保持一定倾角情况下，完成转向运动以及在受到外界瞬时100N干扰力下保持转弯平衡稳定，验证了所建立的平衡车的转弯动力学模型的正确性。与一般的近似线性化方法对比，在使用多输入多输出系统的输出反馈线性化算法设计控制算法，不需要做出其它线性近似处理，取得了更好的效果。