基于过程仿真的密集阵目标拦截效能研究
尹 晋
(91404部队,河北秦 皇岛 066001)
1 引言
密集阵是一种近程防御武器系统,是一种全自动快速反应、密集发射的近程防空反导火炮,在舰艇和要地防御中得到广泛应用。密集阵系统由搜索雷达、跟踪雷达、火炮三位一体的形式组成,能以全自动的方式进行目标搜索、发现、威胁估计和指示、威胁捕获和确认、开火、闭环瞄准、摧毁目标、杀伤评定。其原理框图如图1所示。
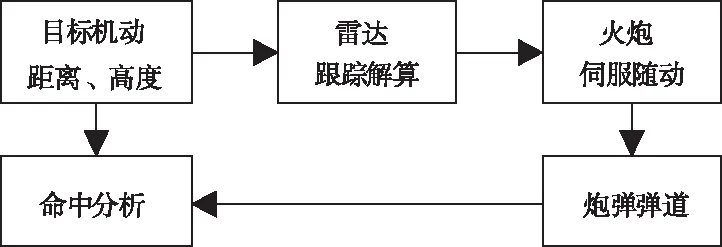
图1 密集防空火炮命中分析要素结构图
密集阵系统目标拦截性能主要包括跟踪雷达的目标距离与方向探测精度、目标运动预报信息处理、火炮随动速度和精度、发射速率、炮弹初速与空气阻力系数等。对于目标不同的速度、尺寸大小、突防机动样式,在目标不同距离和高度上的单位时间内命中枚数,都具有不同的效能体现。对密集阵作战效能的研究有理论分析和试验两种方法。
在密集阵系统目标拦截的理论研究方面,国内学者进行了许多工作。文献[1]基于VR-Force仿真软件和概率模型,对不同入射角导弹的拦截效率进行了研究;文献[2]基于Sim000仿真软件和建立的雷达跟踪与滤波模型、开火时机决策模型、作战流程Euler网模型,对导弹突防概率进行了研究。目前国内研究基本上都是针对直线运动的导弹目标,未充分考虑火炮随动控制和弹道性能特点[3]。
本论文研究将针对目标不同的突防机动样式,结合拦截炮弹弹道和火炮随动系统的建模,通过仿真实验,试图得出对不同机动样式、尺寸大小的目标,在距离、高度上的单位时间内命中枚数的分布。
2 目标突防机动与雷达跟踪
目标突防机动考虑三种典型的情况:直线机动、水平面圆周机动、水平面和垂直面蛇形机动。直线机动时目标以定速、定向、定高运动,如导弹制导开机前的运动;水平面圆周机动时目标以固定的角速度作转向、定高运动;水平面和垂直面蛇形机动时目标以正弦规律变化的水平和垂直角速度在空间进行蛇形曲折运动。
通过雷达跟踪实时获取得到目标距离、方位、俯仰角信息。雷达跟踪的目标是预报目标的运动,为火炮随动提前瞄准提供依据,消除炮弹弹道运动耗时的影响[3]。目标运动预报的研究比较广泛深入[4]-6],涉及雷达回波频域分析、运动特性分析、卡尔曼滤波等方法。针对本文研究中目标速度微变但机动多变的特点,采用目标运动回归分析方法。
雷达探测跟踪中目标方位、仰角、距离在真实数据基础上加入随机误差,得到当前时间前一段时间内目标的信息{ti,di,αi,βi|i=0,1,2,…,n-1},其中t、d、α、β分别是时间、距离、方位角、俯仰角,按下式计算得到时序上的目标坐标
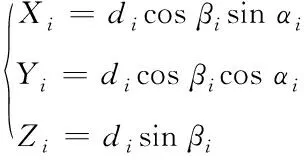
(1)
对{ti,Xi,Yi,Zi|i=0,1,2,…,n-1}中的三个坐标数值分别进行时间拟合,得到坐标随时间变化的解析表达。采用时间的2次函数进行拟合,以X坐标为例,n组数据(ti,Xi)(i=0,1,…,n-1)进行拟合后得到3个参数ak(k=0,1,2)表示的拟合曲线
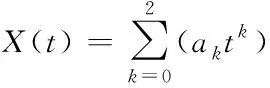
(2)
为确定拟合参数,定义拟合误差为
当e最小时
即
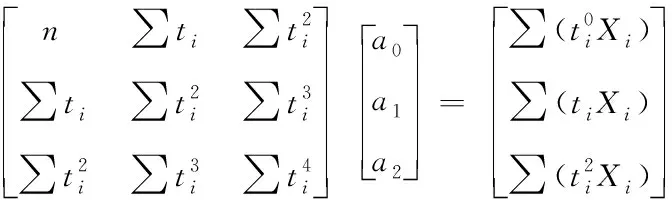
(3)
由此可求得3个拟合参数ak(k=0,1,2)。
图2是基于数据拟合的目标轨迹预报仿真效果图,上下部分分别是2秒内目标运动轨迹的正视图和俯视图。在1秒时进行目标航迹的预报,圆点是根据雷达根据1s内探测的目标位置拟合得到的目标航迹。

图2 目标不同机动下运动轨迹预报仿真效果
3 火炮弹道
根据火炮弹道学理论[7],炮弹从火炮出膛后,弹道的初始条件是出膛的初速度和方向,然后在重力和空气阻力作用下,产生弯曲的弹道。记出膛速度为V0,炮膛方位角α、俯仰角β,炮膛水平角速度ωα、垂直角速度ωβ,炮管长度L。则炮弹初始位置坐标为
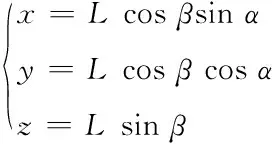
(4)
位置坐标对时间求导,得出炮管末段转动的线速度
在此基础上,叠加炮膛静止时的炮弹出膛速度,得到炮弹初始速度为:

(5)
炮弹所受空气阻力与其速度的平方成正比,动力学、运动学模型分别为:
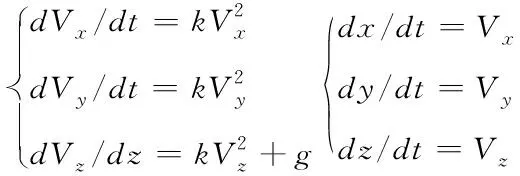
(6)
图3是采用以上模型计算得到的炮弹垂直面的弹道轨迹,发射仰角为5°~60°,间隔5°,轨迹上小圆点为间隔0.5秒的位置。图4是计算得到的不同发射仰角下炮弹速度随时间的变化曲线族。从弹道可见,密集阵拦截攻击是一种典型的提前角攻击。
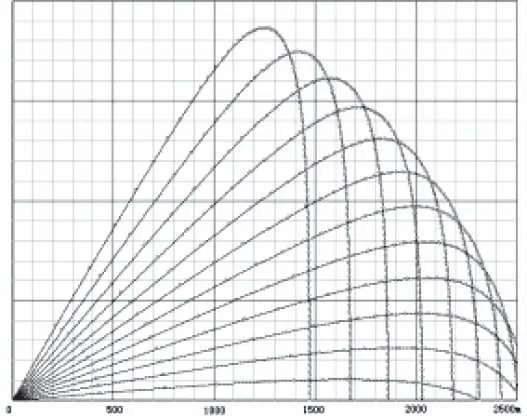
图3 炮弹垂直面弹道模型计算结果
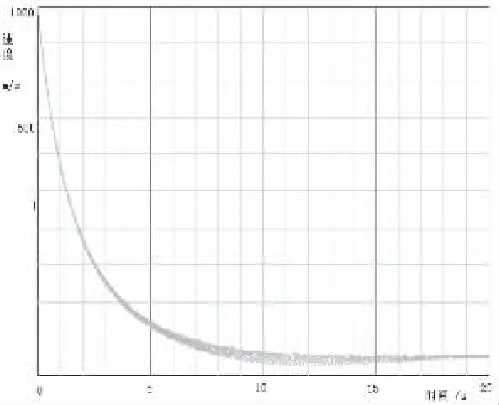
图4 炮弹速度变化计算曲线
4 火炮伺服随动控制
火炮伺服随动是根据连续高速射击的方位角和俯仰角要求,实时、动态、连续地控制,使在规定的炮弹出膛时间到达期望的方位角和俯仰角。炮弹出膛时间以射击速度为恒定间隔,如10,000发/分钟的射击速率下,这一间隔为6ms。
根据密集阵近程防御武器系统的闭环火控原理[8],研究中采用二阶系统进行等效模拟,参照某型火炮随动系统的分析[9],建立火炮随动控制模型。
火炮控制模型考虑转动惯量和阻力矩影响,阻力矩与角速度成正比,有:
水平方位角控制模型
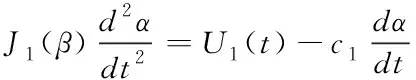
(7)
垂直俯仰角控制模型

(8)
其中,J1(β)为随俯仰角β变化的水平方向转动惯量,J2为垂直方向转动惯量,U1(t)和U2(t)分别是水平和垂直方向的控制力矩,c1和c2分别是水平和垂直方向的阻力矩系数。以水平方向控制为例,上式变换为
其中,K1=1/c1,T1=J1/c1。在控制量U1固定的情况下,得到方位角及其角速度随时间的变化为
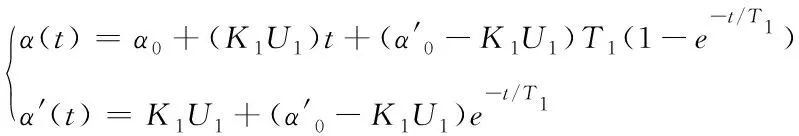
(9)
由上式可知,t>>T1后稳定的转动角速度为K1U1,是由控制力矩和阻力矩系数确定的;T1是惯性产生的时间小于,T1越大系统响应越快。
图5是火炮伺服随动角度的仿真效果,其中小圆圈表示射击间隔处期望的角度,曲线是控制下角度随时间的变化。
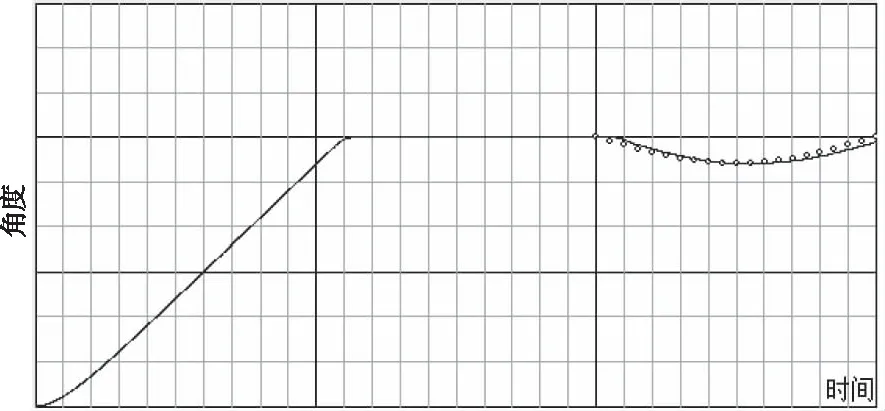
图5 火炮伺服随动角度仿真效果
5 构建仿真软件
根据密集阵连续快速射击过程原理,在雷达对突防机动目标的跟踪和运动轨迹预报基础上,需要以密集阵射击间隔为周期、以炮弹垂直面弹道为依据,确定炮弹与目标相遇的射击时间、仰角、方位角,产生射击队列控制数据;周期性地控制密集阵火炮进行两个方向的角度调整,满足射击队列控制数据中时间、仰角、方位角的要求;计算每个周期中各炮弹和目标的最小距离,进行命中判断分析。最终通过多次拦截过程的仿真,统计得出目标在距离、高度范围内的单位时间炮弹命中枚数。
仿真软件流程如图6所示。

图6 密集阵拦截效能分析的过程仿真流程
5.1 仰角弹道数据集
采用拦截炮弹弹道模型,预先计算炮弹垂直面内不同射击仰角下离散时间的弹道数据,存入弹道数据集。为射击要素计算提供依据,提高射击要素计算的效率。
仰角弹道数据集格式为
Ddd={Avi: {Tij,Dij,Hij|j=1,2,…,mi} |i=1,2,…,n}
其中,Avi为n个从小到大排序的发射仰角,Tij、Dij、Hij为发射仰角Avi弹道中mi个时刻、导弹水平距离、高度数据。
发射仰角采用间隔为1°,弹道时间间隔△t根据密集阵射击速率确定,10000发/分钟时△t=0.006秒。
5.2 射击要素计算
根据目标预报轨迹预报的拟合公式,得到预报轨迹的数据:
TAR={Pk(tk,TXk,TYk,TZk)|k=1,2,…,m)}
时间起点取当前时刻为0,采用下式计算指标位置

(10)
由此计算得到m个预测目标轨迹点的时间存在一定误差,采用下式进行修正
tk=tk-1+|Pk-1Pk|/vtar
(k=2,3,…,m)
(11)
对于(k,k+1)段目标轨迹,采用垂直面弹道数据集,从弹仰角道i=1开始,i=i+1递进搜索。如果弹道段Ddd(i)的高度和射程与(k,k+1)段目标轨迹高度和射程不存在交集,则i=i+1继续递进搜索。否则进行弹道Ddd(i)各段(j,j+1)与目标预报轨迹(k,k+1)段的高度和射程交集搜索。弹道段和目标轨迹段不存在交集时,j=j+1,直到j=mi-1。存在交集时,如果弹道时间Ddd.Tij>tk说明射击已迟后,结束本弹道,i=i+1继续递进搜索;否则判断弹道(j,j+1)段与目标(k,k+1)是否相交,相交时结束i,j,k的全部搜索,否则继续搜索。
通过上述搜索确定了弹道Ddd(i)的(j,j+1) 段与目标(k,k+1)相交,且弹道所需时间小于目标到达所需时间,说明可以通过延时发射使炮弹接近目标。计算这两段的最小距离,和最小距离时两者的时间、位置,在此基础上进行弹道修正。
由于射击仰角弹道数据集存在仰角间隔,最小距离处炮弹位置位于相邻两仰角的弹道之间,因此需要进行射击仰角修正。同时,上述搜索和求解都是在炮弹垂直面内进行的,未考虑射击方位角,因此需要计算射击方位角计算。
垂直面内弹目最小距离处弹目矢量记为r*,如图7。由三角形余弦定理计算矢量r到发射位置的夹角△β作为射击仰角修正量。如果r*朝上,射击仰角β=Avi+△β;否则β=Avi-△β。计算三维空间中弹目最小距离处目标预报位置(TX*,TY*,TZ*),射击方位角取α=atan2(TX*,TY*)。则理论上采用(α,β)发射角的炮弹应该正好命中目标。
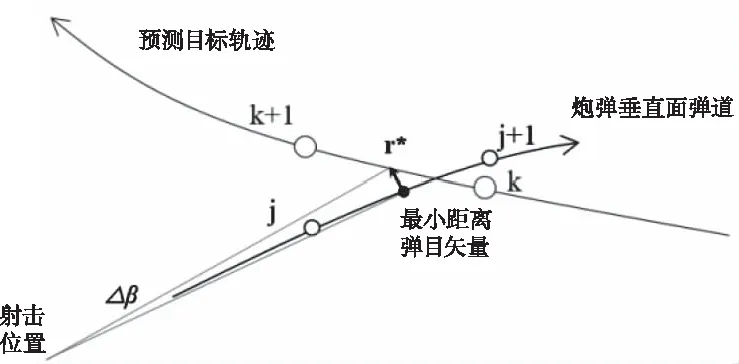
图7 弹目最小距离处垂直面态势
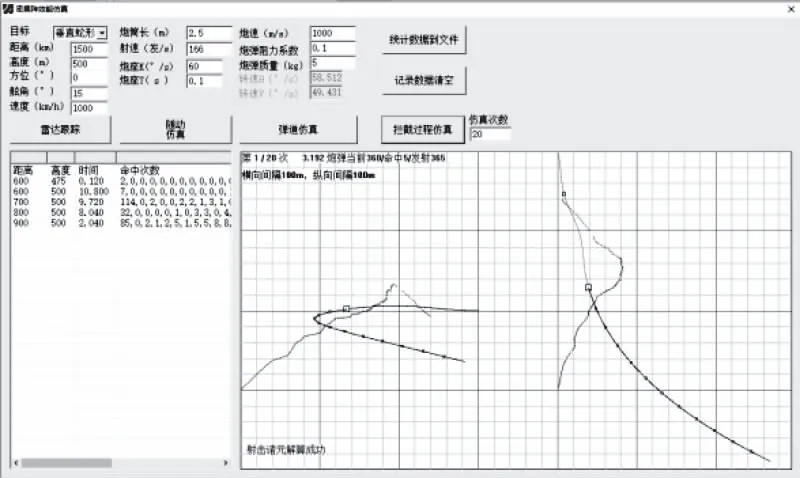
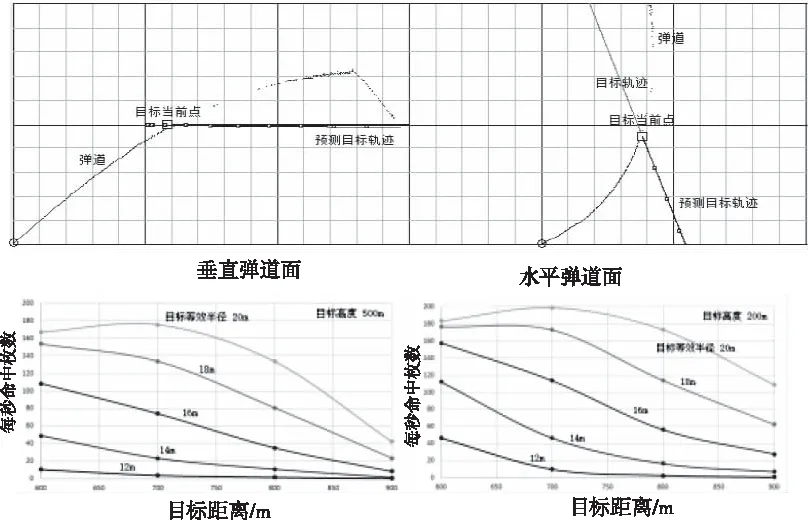
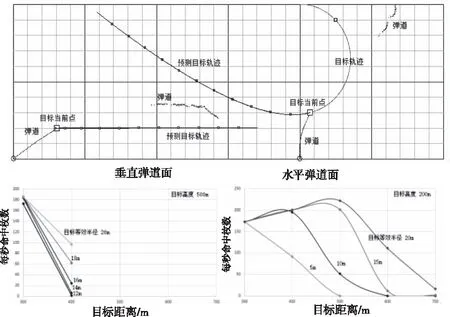
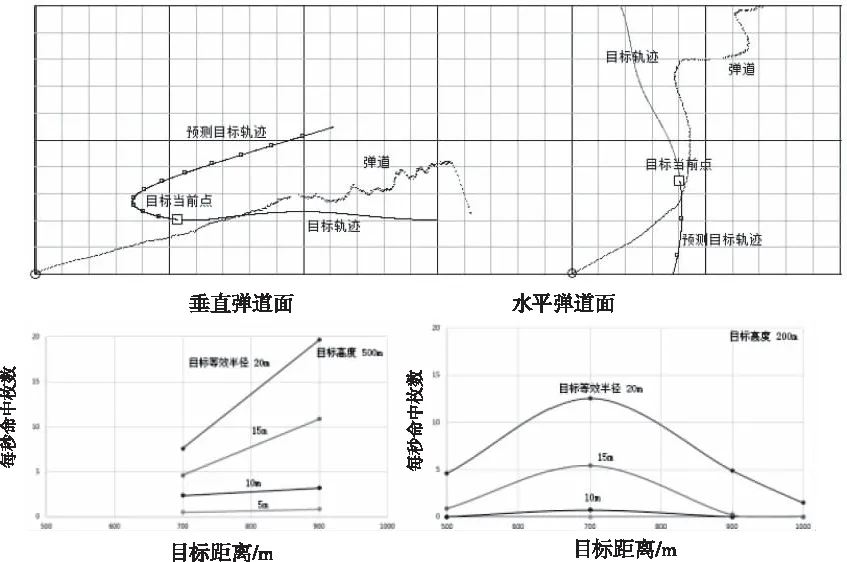
将计算得到的最小弹目距离处弹道时间、目标时间分别记为T*和t*,T* 在每个仿真周期中,从射击队列中搜索当前时间射击的方位俯仰角,产生一个新的炮弹仿真实体。然后从射击队列中删除射击时间为当前时间的记录。 在每个仿真周期中,射击队列中首个记录为火炮随动的目标,记计划时间与当前时刻间隔为t。按式(9)计算t时间后角度变化量 Δα(t)=α(t)-α0 (12) K1和T1的取值可以U1=1作为参照,U1控制量∈[0,1]。 图8是按照上述描述所建立的仿真软件运行界面图。 图8 仿真软件界面 采用开发的仿真软件进行目标三种突防机动过程仿真,得到拦截效能结果。目标初始距离取1500m,速度1000km/h,平面圆周机动时水平角速度45°/s,平面和垂直面蛇形机动时水平和垂直最大角速度取10°/s和5°/s;火炮最大转速60°/s,射速166枚/s(10000发/分钟),出膛速度1000m/s。目标航迹预报采用前1秒内数据进行拟合。 对每个目标机动想定进行20次仿真,每次仿真进行1s后开始射击,当目标距离由小变大或分时间大于5s时仿真结束。以下三图是针对目标的三种突防机动得到的仿真效能结果。 图9 目标直线机动突防 图10 目标圆周机动突防 图11 目标蛇形机动突防 通过上述结构对比,得到以下结论: 1)目标曲线机动突防时,单位时间内命中概率明显下降,三种目标突防机动的命中概率依次大幅度降低。目标曲线机动越强,则目标航迹预报精度越低,射击误差越大。 2)对低空目标的命中概率一般都要大于对高空目标的命中概率。目标高度越大,则采用的射击仰角越大,炮弹用时越长,命中概率越低。 3)目标尺寸越小,则命中概率急剧降低。 采用装备原理建模和作战过程仿真的方法,得到密集阵目标拦截的作战效能,是一种经济高效的效能研究方法。 仿真研究很难完全面准确地处理各种因素的影响,如目标航迹预报的数据处理方法、雷达探测和火炮射击方向的随机误差、目标在炮弹方向上的真实距离。但仿真研究方法至少揭示了命中概率与目标机动和态势关系的一般规律,进一步研究需要结合实装试验数据进行效果的数据修正,以及根据目标外形和尺寸对命中进行进一步的细化处理。5.3 火炮随动控制
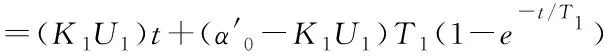
6 仿真结果
7 结束语

