让学生在游戏中感悟概率的内涵
徐亚艳





[摘 要]在课堂中,教师作为探究活动的策划者、引导者,应从动手实践和体验认知环节切入,引导学生对活动结果进行猜想、验证、总结,并提炼出数学规律,掌握知识的概念,让学生的数学活动能力和归纳能力得到提高,学习目标得以实现。
[关键词]概率;抓球;可能性
[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068(2022)05-0075-03
教师出示图1并用中秋节话题引入:“中秋节快到了,某商场举行‘迎中秋抽大奖’活动,购物金额达200元的消费者有机会参与转圆盘抽奖活动。指针落在矩形区域,就能获得月饼一盒。预测一下中奖的概率。”学生窃窃私语,片刻之后接连举手。一个学生说:“不可能中奖,因为指针只能落在圆盘中,无法落在矩形中。”
兴趣是最好的老师。一开始,教师就用有意思的“转圆盘”游戏吸引学生的注意,借助生活情境让学生用“可能、不可能”来表述事件发生的概率,鼓励学生大胆发言,说出自己的第一想法,为后续学习打好基础。
一、合作探究
师(出示图2):探究一下另一种抽奖方案,用这样的圆盘抽奖,参与抽奖的消费者会有机会得到月饼吗?指针有可能落在哪个区域?
生1:有2种可能,可能落在蓝色区域或黄色区域。
师:指针落在哪个区域的概率大?落在哪个区域的概率小?
生2:指针落在蓝色区域的概率大,落在黄色区域的概率小。
师:你能说明理由吗?
生2:因为蓝色区域面积大,黄色区域面积小,指针落在蓝色区域的概率就比较大。
教师板书:(1)结果有2种可能;(2)指针落在蓝色区域的概率大,落在黄色区域的概率小。
师:你观察得真细致,分析得头头是道。(板书:概率)
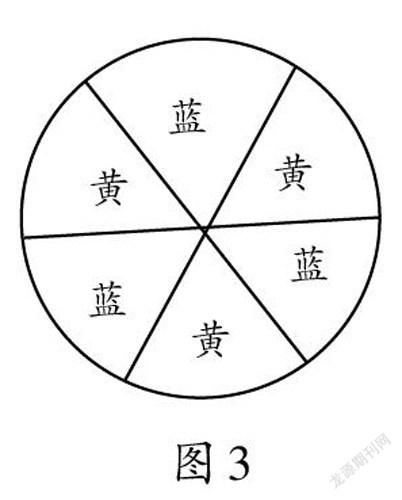
师(出示图3、图4、图5):还有三种抽奖方案,同学们分别说一说在这些方案中,指针落在哪个区域的概率大?落在哪个区域的概率小?解释一下原因。
(学生以小组为单位自主探究,并派代表发言)
生3:图3中蓝色、黄色区域面积各占一半,这样指针落在蓝色区域和落在黄色区域的概率相等。
生4:图4中蓝色区域的面积比黄色区域的面积大,这样指针落在蓝色区域的概率大一些。
生5:图5中蓝色区域面积最小,指针落在蓝色区域的概率最小。
师:如果你是消费者,你认为用哪个圆盘抽奖对你最有利?(指针落在蓝色区域即为中奖)
生(齐):选圆盘4(图4)。
师:概率大小与面积大小有什么关系?
生6:哪种颜色区域的面积大,指针落在那个区域的概率就大。
师:是的,在转圆盘抽奖活动中,哪种颜色区域的面积大(板书:面积大),指针落在那个区域的概率就大(板书:概率大);哪种颜色区域的面积小(板书:面积小),指针落在那个区域的概率就小(板书:概率小);面积相同,颜色不同的区域,指针落在哪个区域的概率都相等(板书:相等)。
师:下面我们就一起来通过抓乒乓球的游戏来检验一下上述结论是不是具有普遍性。
【评析】
上述环节,学生借助已有经验,经过简单的分析、推测就概括出了一般规律,关键是能够说出心中所想。
这种依据面积来判断概率大小的问题就是概率论中的“古典概型”问题。指针落点的所有可能情况都无法统计清楚,也无法用具体数字表示,也就是这个事件不是由若干个可计数的基本独立事件组成。这种“古典概型”问题符合直观判断和合理猜想的教学需要。学生刚开始学习“可能性”时,不懂得独立重复事件的数量以及事件总和与概率的数量关系,而且这种关系也很隐蔽,必须通过大量独立重复实验,统计出各事件发生次数与实验总数的比才能求出,实验次数越多,得出的结果越准确。如将一枚硬币向上抛,落下后正面朝上和反面朝上的可能性都是[12],[12]这个数据需要重复多次实验才能归纳推知。若抛100次硬币,统计发现正面朝上和反面朝上的情况几乎各占一半(也许存在些微误差,但是基本情况不会变),这是因为抛一枚硬币只有正面朝上、反面朝上两个平等的独立事件,事件总和为2,而其中一类事件数量为1,因此某一事件发生的概率为[12]。然而这个理论对学生来说很难理解,所以教师先用无法计算独立事件数量的“古典概型”问题导入“可能性”,不但降低了授课难度,还让学生通过观察、推理发现概率的计算与各类事件体量的大小有关,为后来的“可能性”定量分析打下基础。
二、抓取乒乓球游戏
师:把5个黄色乒乓球放入黑色布袋,然后任意抓取一个,猜猜它的颜色。
生1:必然是黄色。
师:是吗?将它放回后再抓取一个呢?会抓出白色乒乓球吗?
生2:不可能。
师:凭什么断言抓取到的是黄色乒乓球呢?
生3:因为袋子里只有黄色乒乓球。
师(出示图6):这里有5个黑色布袋,各黑色布袋里放乒乓球的情况如下。
师:大家猜测一下,若从每个黑色布袋里任取一个乒乓球,各乒乓球可能是什么颜色?请记录自己猜测的结果。
(学生猜测)
师:我发现大家都有自己的判断。想不想证实一下自己的猜想?
生(齐):想。
师:现在,各小组按图摆出5个黑色布袋,各组组员轮流抓取乒乓球,一次只能抓取一个。抓乒乓球前先摇匀,取出乒乓球查看后再放回布袋,下一位同学继续抓取。请小组长记录各组员抓取乒乓球的情况。
(小组探究)
师:各组观察实验记录单,概括规律。
生4:我從第一袋里抓取到的乒乓球必定是黄色乒乓球。
生5:我从第二袋里抓取到的乒乓球必定是白色乒乓球。
生6:我推测从第三、四、五袋里抓取乒乓球,黄、白两种颜色的乒乓球都有可能被抓到。
师:那么,在第三、四、五袋中,从哪个布袋里抓取到白色乒乓球的概率最大?
生7:第五袋,因为在第五袋中,白色乒乓球的数量远多于黄色乒乓球的数量。
师:白色乒乓球的数量多就表明抓取到白色乒乓球的概率——
生(齐):大!
师:概率的大小与什么有关?
生8:我认为概率的大小与探究对象数量的多少有关。
师:当黑色布袋里只有一种颜色的乒乓球时,抓取到的一定是这种颜色的乒乓球,不可能是其他颜色的乒乓球。当黑色布袋里既有黄色乒乓球又有白色乒乓球时,抓取到的可能是黄色乒乓球,也可能是白色乒乓球。如果白色乒乓球的数量比较多,那么抓取到白色乒乓球的概率大(板书:概率大)。如果白色乒乓球的数量比较少,那么抓取到白色乒乓球的概率就小(板书:概率小)。
【评析】
本环节教师设计了“猜想”“抓取”的活动,首先调动学生猜想的热情,唤起学生的知识记忆,激发他们的学习兴趣;然后通过小组合作,使学生认识到亲自抓取乒乓球才能验证猜想,这时的操作活动就成为学生的需求,学生会带着目的和疑问去探究。
第一阶段用“古典概型”问题完成“可能性”教学的铺垫后,学生对“可能性”有了初步认识,并且发现概率大小与各类事件本身的体量(面积)有关。第二阶段升入到一般概率计算,此时,探究对象不再是不可计数的面积,而是可以计数的乒乓球,学生对各种颜色的球数有了一个清晰的认识,甚至可以数出各种颜色的球到底有几个,谁多谁少,一目了然。这样教学没有采用重复实验统计法(抓球后将球放回,多次实验,统计抓到各种颜色的球的次数和实验总次数,再算出二者的比值)。因为统计是小学五年级才出现的内容(条形统计图和折线统计图),学生的思维里还没有形成统计的科学概念,更别提运用统计结论来分析问题。因此,采用保守教法,让学生直接凭经验和常理推测来达到合理估测“可能性”的目的,综合了感性和理性认知,也达到了教学目的。
三、试一试,融合试验
师:如果我将8个白色乒乓球、4个黄色乒乓球、2个红色乒乓球放入一个黑色布袋里,摇匀后,抓取的结果可能有几种情况?
生1:抓取到白色乒乓球的概率最大。
生2:抓取到红色乒乓球的概率最小。
生3:抓取到黄色乒乓球的概率比抓取到白色乒乓球的概率小,但比抓取到红色乒乓球的概率大。
师:真棒!你们的说法反复印证了一个道理——有些事情的结果是不确定的,例如从有黄色和白色乒乓球的黑色布袋里抓取乒乓球时,你就无法确定抓取出来的乒乓球是黄色的还是白色的。通过验证猜想,我们搞清楚了抓取不同颜色的乒乓球的概率是有大有小的。
【评析】
这个时候,学生的认识就上升到了理性认识,原本的定性分析也会上升到定量分析。前面只有2种颜色的球,这次增加到3种颜色,这绝不是简简单单的量变,而是量变引起的质变,从3种颜色分析抓取概率,那就不仅是比多比少的问题(数量多的抓到的概率大一些,数量少的抓到的概率小一些)。放入3种颜色的乒乓球,那么概率多与少之间不再那么模糊,而是变得相当具体,几乎可以量化,如一个盒子里装有5个白球、4个红球、6个蓝球,那么抓到蓝球的概率大于抓到白球的概率,也大于抓到红球的概率,而且大多少,也能具体算出。其实,这种推断已经接近概率的精确计算,只要再进一步就能得出抓到每种颜色的球的精确概率。通过大量独立重复实验可以统计出,抓到蓝球的概率是[615],抓到红球的概率是[415],抓到白球的概率是[515],这些都是可以从球的总数上推知的,各种颜色的球数与总球数的比值就是摸到该种颜色的球的精确概率,这与概率学上的“设基本独立事件的总数为m,某类事件独立出现的次数为n,那么该类事件发生的概率是[nm]”的原理是一致的,只不过说法不同。
概率问题可以复杂,也可以简单;可以直观,也可以形象。教师需要拿捏好火候,学生需要把握好分寸。对于小学中的“可能性”,学生不需要计算出精确的概率值,但是要学会比较概率大小,而比较概率大小要从某类事件出现的次数的多少中判断,因为分母都是一样的,只需要比较分子。
学生经过自主探究、小组合作,认识了什么是概率大小,然后通过“试一试”的提升试验,将概率比较从不同空间转移到同一空间,进行混合区分,大大拓宽了思维,深化对概率大小的认识,有利于自身从生活现象中看透数学规律,进一步领会到“数学源于生活”的真谛,有助于建构新知体系。
[ 参 考 文 献 ]
[1] 张建发.聚焦核心素养,彰显数据分析观念:小学“统计与概率”领域教学思考[J].华夏教师,2020(04).
[2] 曹培英.小学数学统计与概率教学研究(五)[J].小学数学教育,2020(Z1).
[3] 林榕.小学数学统计与概率的“真”[J].新教师,2019(05).
(責编 黄 露)

