数学学习在“转换”中迈向深度

史息良 刘玉琴 王留芳

在培养学生数学核心素養的观照下，我们的教学不应只是简单地按照教材编排，把静躺在书本上的知识点一成不变地传递到学生的头脑里储存起来，让学生成为接受知识的“容器”。而是要以教材为载体，在教学知识的同时，更关注知识的深层次问题（比如知识性子、思想、方法、作用等），把外在于学生的、和学生没有关系的知识，在教学中转化为学生主动活动的对象，从而与学生建立起意义关联，并通过学生个体的主动学习转变成学生成长养分，发展数学思维，促进他们数学核心素养的提升。因此，在教学中，教师要会准确地把握教学节奏，对教学内容进行适时的“转换”，让学生的数学学习逐步迈向“深度”，让教学更富含“育人”的课程意义。

一、在“法”与“理”的转换中迈向抽象

张景中院士认为“运算是具体的推理，推理是抽象的计算。”运算的本质是一种数学思维能力或者推理思想，但是运算如果不讲算理，只讲算法，或者学生不懂算理，只会算法，学生就只会照葫芦画瓢，模仿着计算。那么这种运算就不是推理，也不是真正的数学，而只是浅层次的算术。如果学生慢慢学会用抽象和推理的思想方法理解算理，学会说理，就慢慢学会了思考。正因此，计算教学的价值取向，不仅仅是为了运算的正确与熟练，更重要的是让学生体会领悟运算中的原理、推理的思想方法、逻辑关系、规定算法的合理性以及计算的应用。

如，教学“两、三位数除以两位数”时，学生开始学习“整十数、几百几十除以整十数的口算”，并以“60÷20=？”为例题引入。学生通常会有两种方法口算出结果。第一种是想乘法算除法：因为20×3=60，所以60÷20=3，这运用了乘除法之间的互逆关系来运算的。第二种是利用表内除法：因为6÷2=3，所以60÷20=3。但当问起“计算60÷20，为什么可以想6÷2”，学生都不能回答出真正的所以然。其实第二种算法是根据十进位值制计数原则，掌握以分“计数单位”的方式将其转化成表内除法的计算方法，思路更简捷、明了，是教材提倡的主要算法。因此，多“花费”一点时间，选择适合学生理解和接受的认知方式和途径，在教学中“插入”一段“认理”环节，对学生的数学抽象能力和推理能力的培养是十分有价值的。

第一步：具体感知。

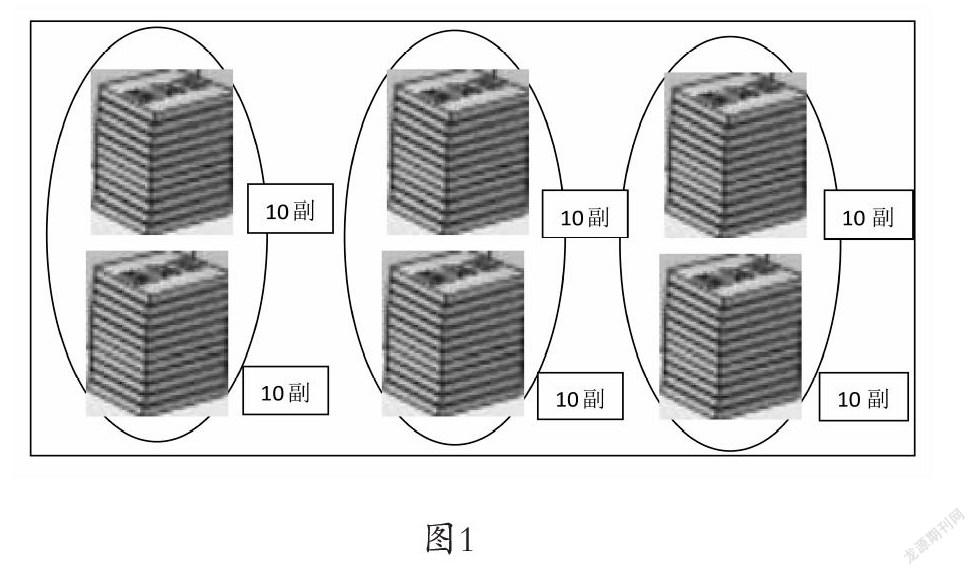
呈现如下数学情境：每20副陆战棋打一包，60副要打几包？（并配图1）

学生会出现两种算式：

（1）60÷20=3，即60副陆战棋，每20副打一包，可以打3包，数学理解就是60个1（即是60），每20个1（即是20）圈作一份，可以圈成这样的3份。

（2）6÷2=3，学生这样解释：6扎陆战棋，每2扎打成1包，可以打3包。这里的1扎就是10副，数学理解就是：6个十，每2个十圈作一份，可以平均分成3份。

经过再次比较，引领学生感悟到在图1情境中，60÷20=3，是以“一”为计数单位来思考进行计算，而6÷2=3是以“十”为计数单位来思考进行计算。

第二步：逐步抽象。

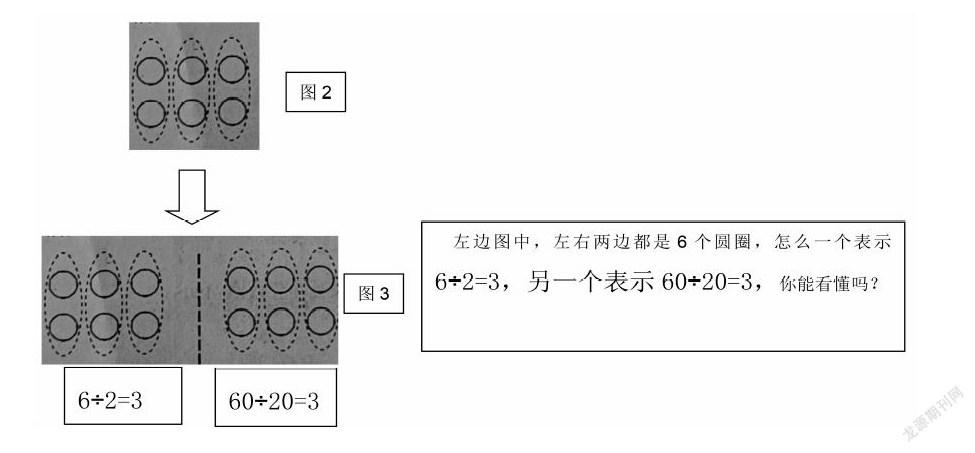
将上面图1先动画演变成图2，再呈现图3。

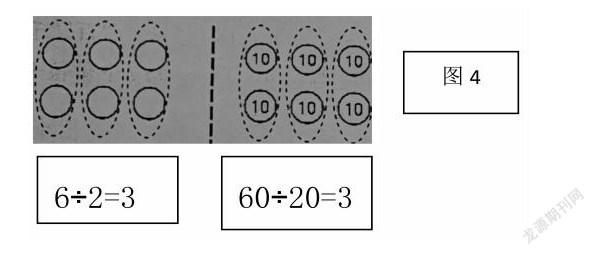
学生交流后明晰：1个圆可以表示1，也可以把1个圆想象成10，6个圆就表示60。接着呈现图4：

第三步：抽象建模。

学生做出了进一步推理：600÷200，6000÷2000，……，最终理解分别以“一”“十”“百”“千”……为单位分，都是6个单位，每2个单位一份，分成3份，都可以想6÷2=3。

从上面的教学过程来看，学生的学习由特例对象到一类对象，思考经历特殊到一般化的推理过程，以算理为基础，逐步归纳抽象为法则，将法则和算理贯通，由具体形象思维逐步走向抽象思维。

二、在“对”与“错”的转换中迈向深刻

美国著名发展心理学家盖耶有句名言：“谁不考虑尝试错误，不允许学生犯错误，就将错过最富有成效的学习时刻。”教学名师华应龙自称“化错人”，他认为：“化错，才是真正的学习。”学习正是一种通过反复思考招致错误的缘由、逐渐消除错误的过程。

特别是在新教师的课堂中，他们往往只注意强调展示学生解题正确的一面。又因为他们对学情的不了解，总是会忽视学困生会发生具有共性错误的地方。

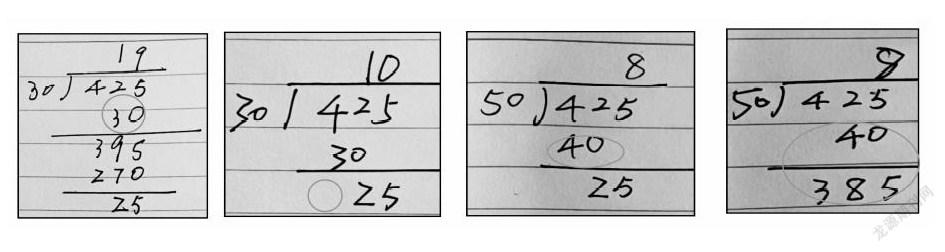
如，在“三位数除以整十数”的教学中，教师总是喜欢只请好学生上黑板演示竖式计算的过程，而忽视了竖式书写过程中的“对位”问题以及“漏写”问题，如下面这些情况：

课堂上如果能在展示“正确”的同时，有意暴露学生的这些错误及其思考过程，组织学生经历找错、纠（说）错、改错的过程，学生将会对计算法则的掌握更牢固，理解更深刻。这其实也是教师课堂教学的“底线思维”，将“补差转差”工作真正落实到课堂上的一种十分有效的方法。

三、在“式”与“事”的转换中迈向理解

数学是系统化了的普通常识。由于小学生的思维处于具体形象思维到抽象思维的过渡阶段，小学数学应是“儿童的数学”，儿童对数学知识的理解、学习与掌握，大多是基于对生活实际问题的理解把握与解决之上的。可以说生活中的“情境故事”是他们数学理解的“支点”与“脚手架”。

如，在教学减法的性质“一个数连续减去两个数等于这个数减去后两个减数的和”，即a-b-c=a-（b+c）时，有老师结合生活中建房时建筑工人“抛砖”的劳动情境帮助学生理解感悟其中道理：从地上的一堆方砖中拿两块抛向二楼的工人（有工人在二楼接砖），力气小点的工人可以把这两块砖分两次一块一块向上抛，力气大点的工人也可以把要抛的两块砖合在一起一下子抛向二楼，前者的抛法相当于a-b-c，后者的抛法相当于a-（b+c），但两种抛法只是方式不一样，结果是一样的。后来学生们把这种方法总结为“抛砖法”。

实践证明，结合这样的说理，学生对减法的性质的理解非常深刻，计算技能的掌握也非常牢固。其实，翻开小学数学课本，我们会发现，小学数学就是结合生活情境故事来教学的。

四、在“点”与“面”的转换中迈向建构

郑毓信教授指出：“数学教学要帮助学生能超出各个具体内容，建立整体性、结构性的认识。”即认识必须由局部过渡到整体，切实避免“只见树木不见森林”的毛病，实现知识的统整与数学素养能力的提升，引领学生进行知识的自主建构，走向深度学习。

如，教学完“多边形的面积”后，教师通常会对多边形的面积进行全面复习，但好多老师又往往会停留在巩固各个图形面积的计算、應用以及通过梳理各个图形面积计算公式的推导过程，来建立图形之间的联系，形成知识学习网络图。

但笔者认为，这还只是相当于回顾梳理了学生的“学习过程”，巩固了“知识点”，还没有达到郑毓信教授所说的“能超越知识学习有更大的收获”。教师如果能运用信息技术手段动画演示，引导学生从“变化发展”的角度，运用观察和比较、分析和联想、归纳和概括等数学思维方法，去发现各图形演变之间的联系，从而更进一步地深入思考和感悟各图形面积计算公式之间的内在联系和本质的一致性。

五、在“繁”与“简”的转换中迈向优化

从“结绳计数”，发展到用“书契”记事，符号、数字示数，不但体现了数学简约和抽象之美的魅力，更表现了人类最高超的智力成就。而在数学教学中，学生对困难复杂问题的思考也正是经历从难到易的过程，对问题的回答经历着从繁到简的表达过程，在横向数学化和纵向数学化的过程中达成解决数学问题的优化。

如，在学习“简单的周期”中，学生先经过观察发现了盆花排列的特点，并用语言描述“盆花每3盆为一组，每组按蓝花、黄花、红花的顺序排列”，接下来回答“按盆花的排列规律，第19盆花是什么颜色的花？”由于是第一次尝试解答这样的问题，对问题的回答出现了多种表达方法：

从学生回答问题不同的表达形式来看，学生的思维进阶有着明显的区别，处于不同的思维水平。方法一有“按图索骥”味道，是用数数的方法寻找问题的答案;方法二和方法三是学生用文字或图形表示不同颜色的花，并用圆圈三盆一圈，已经蕴含了分组的思想方法;方法四是学生根据每组中不同颜色的花的排列位置，用数字来表示，比方法二和三的抽象性更进了一步。但，虽然说方法二、三、四比方法一在思考上有所进阶，但没走出“数数”的低阶思维。当然，这里并不是说前面的几种方法没有价值意义，它们也是学生积极思考的结果，需要鼓励和表扬。同时，教师如果处理得当，这些方法，特别是方法二、三、四可以作为方法五的表征依据，找出解决问题的思路，总结归纳出不同表达方式之间的内在一致性：每3盆花为一组，19盆花可以分成6组，第19盆花就排在第7组的第1个，因为每组中三种颜色的盆花排列的顺序是一样的，所以第7组的第1盆花也就是第19盆花，是蓝色的，方法五中的余数，就对应每组中蓝花所在的位置。

这样，学生对方法五的理解和认同也就水到渠成，学生也肯定能感受到用除法计算是最好、最优、最省事的方法。