探析初中数学中转化与化归思想的实践应用

江苏省无锡市大桥实验学校 陈建忠

初中数学呈现出的主要特征是抽象.很多数学问题需要通过联想、分析、类比等思维进行转换，才能够将原本并不熟悉的问题转化为已经掌握的问题，进而完成问题求解.而数学问题转化的过程被称为转化与化归.从本质上来讲，转化与化归思想充分揭示了联系数学问题实际，完成知识点转化的过程，除却原本就非常简单的数学知识，其他的数学问题都需要经过转化方式来实现求解.可见，转化与化归思想是求解数学问题的基本思想.本文中将就初中数学中的转化与化归思想的实践应用展开详细探讨.

1 复杂问题简单化

初中数学知识教学中，教师通常会引导学生将原本比较复杂的问题以化归方式逐渐转化为简单问题，而学生先解决自己熟悉的简单问题，最终逐步达到解决复杂问题的目的.该种解决问题的方式被称为简单化，是获取复杂问题解题思路的主要依据.

例1如图1，楼梯的高度为2 m，∠BAC=30°，此时在楼梯表面铺设地毯，求地毯的长度.

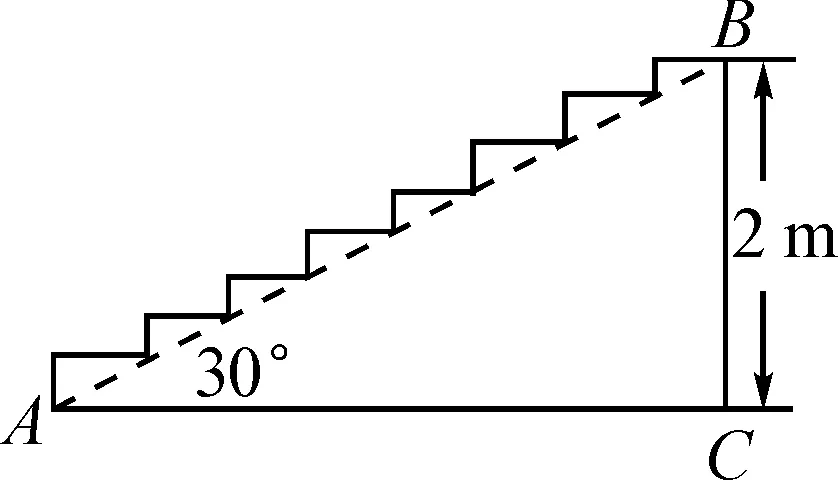
图1

解析：连接AB.

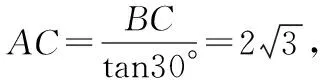
上述解题步骤中，率先考虑的思路是分别求出每个台阶上的地毯长度，然后将这些长度相加.但是，因为不知道每个台阶的具体高度和宽度，因此，如果直接采用这种长度相加的方式求解，思路会受到限制.如果在图形中能够观察到将A，B两点连接以后形成了多个小直角三角形，其中较小的锐角均为30°，而且题目中给出已知条件楼梯的高度为2 m，可以猜测将图形中的小三角形转化为大直角三角形.再思考转化方法，发现将小直角三角形进行平移，能够直接将各个台阶的宽度平移到AC上，与AC的长度相等，将小三角形的高度平移到BC边上，长度与BC边相等.因此，想要求解地毯铺设的长度，只需要将BC边和AC边的长度求解出来，就能够得到地毯的最小长度.经过重新转化和猜想，将原本分散的条件集中起来，最终形成比较完整的解题条件，能够快速解决问题.

2 高难问题概念化

有不少数学问题表面上看难度很大，但如果我们能透过表象，抓住本质，利用已知的概念等基础知识进行化归，难题也就迎刃而解.

例2已知一元二次方程ax2+bx+c=0(a,b,c为常数,a≠0)的根是x1=-3,x2=2，求关于x的一元二次方程a(x-5)2+7b(x-5)+49c=0的根.

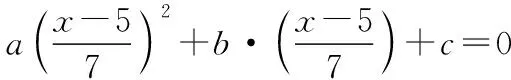
3 疑难问题常规化

有的问题属于非常规问题，我们可以借助化归与转化的方式，让问题变得常规化，从而利用常规的方式解决.

例3如图2，将八个边长为1的小正方形摆放在平面直角坐标系中，若过原点的直线l将图形分成面积相等的两部分，则直线l的函数关系式为________.

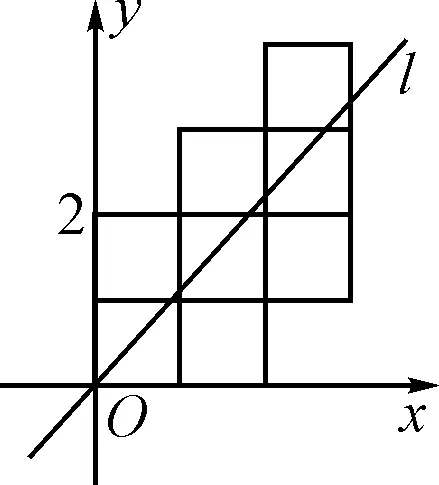
图2

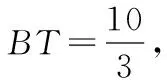
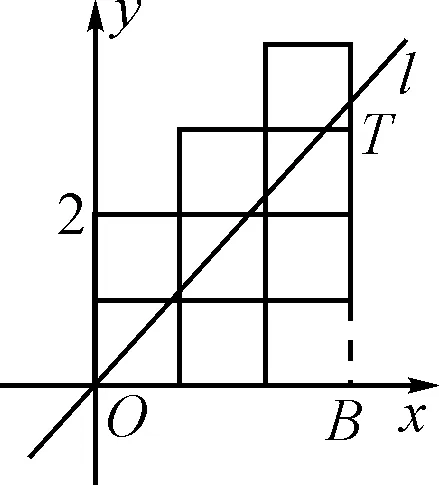
图3

4 变数问题固定化

有些动态变化问题，让学生捉摸不定.这时，我们尽可能利用化归的方式，将问题转换为固定的量.

例4如图4，在ABCD中，∠B=60°，AB=6，BC=4，点E为边AB上的一个动点，连接ED并延长至点F，使得DE=2DF，以EC，EF为邻边构造EFGC，连接EG，则EG的最小值为________.

图4

解析：本题中，EFGC随时处于运动中，EG的长度更是没法确定.设DC与EG交于点T，根据相似，我们可以很快将EG的长度变为问题转化为ET的最小值，从而利用“点到直线的垂线段最短”“平行线间距离处处相等”，求得ET的最小值，从而求得EG的最小值.

5 未知问题已知化

(1)求线段PE长的最大值；

(2)作PF∥AC交BC于F，求EF长的最大值.

6 抽象问题直观化

抽象问题是初中数学中比较常见的问题.很多时候，因为对知识点不熟悉而导致学生不能完全解决相应的数学问题.为提升学生的解题效率，帮助学生形成更加直观的解题思维，可以将抽象问题进行转化，促使其中的已知条件直观化.借助图形方式直观观察抽象问题，了解不同数值之间的关系.

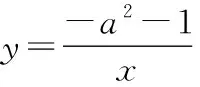
解法1：由k=-a2-1=-(a2+1)<0，得函数图象分布在第二、四象限，而且每个象限内y的数值都会随着x值的增大而增大.

由A(-4，y1)，B(-1，y2)在第二象限，且-4<-1，得0

由C(2，y3)在第四象限，得y3<0.

因此，y3

解法2：将已知条件中的三个点均画在图象上，根据图象可以观察到y3

7 函数问题方程化

对很多学生来说，函数问题都是比较复杂的问题，因为之前较少接触函数相关知识，学生一时之间无法掌握函数知识的规律.在面对函数问题时，学生总感觉力不从心.实际上，函数和方程之间可以实现转化，借助转化与化归思维，将函数问题转化为方程问题，依据自身已掌握的方程知识，完成问题求解.在此过程中，教师对学生进行教学引导，帮助学生形成转化与化归思维.

例7已知关于x的函数y=(m+6)x2+2(m-1)x+(m+1)的图象和x轴总有交点，求解m的取值范围.

解析：若m+6=0，则m=-6，函数y=-14x-5的图象和x轴有相交.所以m=-6符合题意.

若m+6≠0，即m≠-6，则问题转化为关于x的一元二次方程(m+6)x2+2(m-1)x+(m+1)=0总有解.

由Δ≥0，得

4(m-1)2-4(m+6)·(m+1)≥0.

8 总结

总体来说，数学转化思想能够渗透到任何数学问题中，其将大部分学生都不了解且无法解答的数学问题以转化思维进行简单化处理，促使其他的数学知识替代原本的数学条件.而知识转化过程中，学生的数学思维能力增强，数学核心素养也随之提升.学生的数学能力会随着数学知识的学习不断增加，数学思维也会因为数学知识的理解而逐渐迁移.鉴于该种情况，教师在具体教学实践中，需要注意教学方法的选择，给予学生足够的思考空间，让学生将转化与化归思维贯穿于数学解题过程.如此一来，学生能够在面对数学问题时大胆猜测，明确数学化归目标，最终找到解决数学问题的有效途径.