在数学建模中培养学生的创新思维

⦿新疆石河子第一中学 傅祖勇

1 引言

创新思维能力的发展，推动了人类社会的进步.当今社会、科学技术日新月异，靠的就是创新型人才.高中数学教学虽然属于基础教育，但同样肩负着培养创新型人才的重任.那么，高中数学教学创造性思维能力的培养的落脚点在何处呢？笔者认为，教学中，教师应引导学生做到以下三点：一是发挥想象能力，培养直觉思维；二是构建建模意识，培养转换能力；三是以“构造”为载体，培养创新能力.下面谈谈具体做法，不当之处，敬请斧正.

2 发挥想象能力，培养直觉思维

追溯数学的发展历程，我们可以发现，不胜枚举的数学发现往往来自于数学家的直觉思维.史上有名的有笛卡儿坐标系、费尔马大定理、歌德巴赫猜想以及欧拉定理等，这些非凡的“发现”不是数学家通过逻辑思维得到的，而是他们经过细致观察、反复对比、深刻参悟最终数学灵感勃然而出的.在数学建模教学中，教师应引导学生进行直觉思维和直观想象，让学生提出独特的见解，通过建立数学模型来快捷地解决问题，从而实现沟通数学知识内在的联系，激发学生创新思维，提升学生数学能力的目的.

例1除错位相减法之外，你能求S=1+2x+3x2+4x3+……+nxn-1(x≠0且x≠1)吗？

学生直觉：可以将S=1+2x+3x2+4x3+……+nxn-1(x≠0且x≠1)看作某函数的导函数，于是想到构造一个新的函数，借助导数巧妙地解决问题.

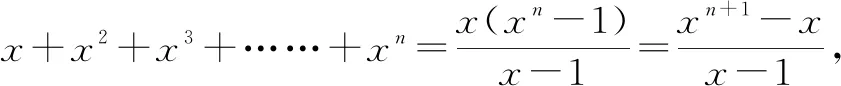
由于本题解答要求避开“错位相减法”，所以学生解答时必须另辟蹊径.学生借助直觉思维，根据所求代数式的特点，想到通过构造函数并妙用导数来解决，可谓新颖自然，巧夺天工，毫无斧凿之迹，怎不令人拍案叫绝！反映出学生善于观察又积极想象的思维品质.试想，假如教师在日常教学中没有一定量的建模训练，他们能“创造”出如此“高大上”的优美证明吗？大数学家泰勒曾经说过，丰富的知识和经验是产生新的联想和独创见解的源泉.

高中数学内容丰富，思想与方法也千姿百态.从一个问题出发，联想到另一个问题，并建立新的数学模型，这种创造性思维的形成往往离不开直觉思维.因此，在数学建模的教学中，教师应重视稍纵即逝的直觉思维的培养.

3 构建建模意识，培养转换能力

恩格斯说过，数学形式的相互转化，不是一种无聊的游戏，而是体现了数学中的平衡关系，如同物理中的“杠杆原理”.一旦离开这个原理，数学就会“搁浅”.而数学建模从本质上看，就是实现实际问题与数学问题之间的转化，因此在数学教学中，我们要注重这种转化，并用好这根“杠杆”，这对培养学生的创新思维意义非凡，同时从应试角度看，对提高学生的解题速度也大有益处.

在函数模型的教学中，笔者给学生举了一个“洗衣问题”的例子：现在有一桶水，需要洗一件衣服，是直接将衣服放入一桶水中洗呢，还是将一桶水一分为二，洗涤两次？哪种洗法的效果好？答案自然是不言而喻的，你能从数学角度来分析并解决这个问题吗？

例2衣服洗涤甩干后需要多次漂洗，如果每次漂洗后衣服上的残留物都是均匀分布的，而且每次漂洗并甩干后衣服中含有的水分和残留物的重量也相同，也就是说每次漂洗前后的衣服上的残留物的含量百分比一致.现有一台全自动小天鹅洗衣机，假定漂洗的用水总量为a，漂洗并甩干的次数定为3.为了让漂洗后衣服中残留物最少，请同学们想一想，如何确定每次漂洗的用水量？

生1：设每次漂洗并甩干后衣服中的残留水分(含残留物)的重量为m，洗涤并甩干后(漂洗前)衣服中残留物(不含水分)为n0.3次漂洗并甩干后衣服中的残留物(不含水分)分别为y1，y2，y3，3次用水量分别为x1，x2，x3(以上各量单位相同)，则由每次漂洗前后残留物的重量百分比浓度相等可知：

师：本问题的关键是利用每次漂洗前后残留物重量的百分比浓度相等来建立关系式，请同学们思考这是为什么？

通过大家的集思广益，得到了本题的推广结论：

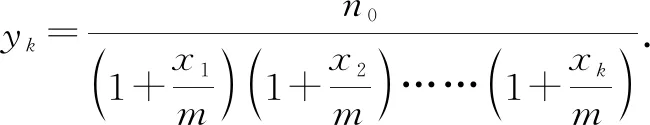
通过实际问题转化为数学问题，利用数学手段，问题似乎已经解决.从理论上讲，定量的水漂洗次数越多，残留物就越少.但全自动洗衣机通常设定为3次漂洗，这是为什么？这又是一个日常生活中的问题，再次激发出学生探究数学的热情，显然这个问题是刚解决的问题的进一步深化，笔者让学生课后进一步研究，于是把学生数学转化能力向更高的层次推进.

4 以“构造”为载体，培养创新能力

所谓“建模”，顾名思义就是构造模型，说来简单，但模型如何构造并非一蹴而就的容易事，这需要学生有足够强的构造能力.而这种能力同样离不开教师在课堂教学中的着力培养，教师应该精选教学素材，以“构造”为载体，培养学生的创新能力.

足球运动深受高中生喜爱，于是笔者提出了如下关于足球的问题：

例3如图1所示，甲方球员A把球传给甲方球员B，乙方的球员C出击阻断该球.球员C断球是否成功，主要由以下因素确定：△ABC的形状、传球的速度、传球的轨迹，还有球员奔跑的速度、球员C的出击角度、球员们反应的时间、比赛时的天气等.我们为了简化问题，提出如下几个假设：首先不考虑客观因素；其次把球员反应时间当成零，并且球员奔跑速度都相等，且他们与球在同一个平面上作匀速直线运动.在这样的假设下，球员C可否成功断球的主要因素，一受△ABC的大小与形状的影响；二受该球员奔跑速度的制约；三还得看传球速度；最后还要看球员C出击的角度.于是，我们可以把球员断球问题，通过数学建模，转化为纯粹的数学问题：

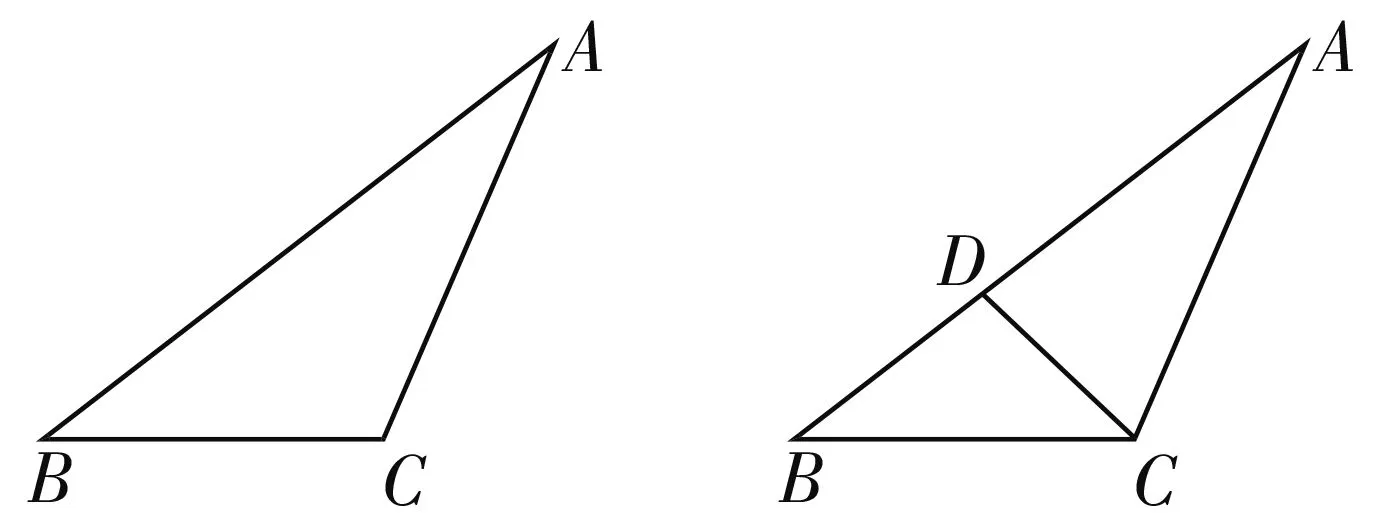
图1 图2

问题1：如图2所示，甲方球员A把球传给本队同伴B，而乙方球员C想抢断传球，在∠A与θ(θ=∠ACD)满足何种条件的时候，球员C才可能实现断球目的？假设A=28°，B=40°，球的速度是16 m/s，球员C的速度是8 m/s，试求球员C出击的方向.

问题2：若依然假设∠A=28°，∠B=40°，球的速度是16 m/s，球员的奔跑速度是8 m/s，试问：

(1)假如球员B积极回抢，那么他能否成功反断球？

(2)球员C由哪个方向出击，他肯定能成功阻断球？

本问题完全数学化后，就是一个解三角形和平面几何问题.由此可见，要把一个实际问题转化为数学问题，首先应该从题目的实际出发，确定选择何种数学模型，依据删繁就简原则，通过主观“构造”，让其显出数学的本质.我们还可以改变假设的条件，如本例中球员对球作出反应的时间，让球员们奔跑的速度各不相同，由于受空气阻力的影响，还可以将球的速度变为减速运动等，于是球员成功断球的条件就变得异常复杂了，这样对学生的创新思维提出了更高的要求.但只有循序渐进，学生的创新性思维能力才能提高.

以上几个例子告诉我们，观察能力的培养与思维能力的培养，在数学建模教学中同样重要.教师只有在数学建模中引导学生眼、手、脑三者联动，创新思维的培养才能落地生根.